§ 13. Корреляционное отношение как мера корреляционной связи. Достоинства и недостатки этой меры

В предыдущем параграфе установлено: прит η=0 признаки не связаны корреляционной зависимостью; при η=1 имеет место функциональная зависимость.

Убедимся, что с возрастанием η корреляционная связь становится более тесной. С этой целью преобразуем соотношение D_общ = D_внгр + D_межгр так:

D_внгр = D_общ [1-( D_межгр/ D_общ)],

или

D_внгр = D_общ (1- η²).

Если η→1, то D_внгр → 0, следовательно, стремится к нулю и каждая из групповых дисперсий. Другими словами, при возрастании η значения Y, соответствующие определенному значению X, все меньше различаются между собой и связь Y с Х становится более тесной, переходя в функциональную при η =1.

Поскольку в рассуждениях не делалось никаких допущений о форме корреляционной связи, η служит мерой тесноты связи любой, в том числе и линейной, формы. В этом состоит преимущество корреляционного отношения перед коэффициентом корреляции, который оценивает тесноту лишь линейной зависимости. Вместе с тем корреляционное отношение обладает недостатком: оно не позволяет судить, насколько близко расположены точки, найденные по данным наблюдений, к кривой определенного вида, например к параболе, гиперболе и т. д. Это объясняется тем, что при определении корреляционного отношения форма связи во внимание не принималась.

§ 14. Простейшие случаи криволинейной корреляции

Если график регрессии = f(х) или = φ(у) изображается кривой линией, то корреляцию называют криволинейной.

Например, функции регрессии Y на Х могут иметь вид:

=ах²+bх+с (параболическая корреляция второго порядка);

=ах³+bх²+сх+d (параболическая корреляция третьего порядка).

Для определения вида функции регрессии строят точки

(х; ) и по их расположению делают заключение о примерном виде функции регрессии; при окончательном решении принимают во внимание особенности, вытекающие из сущности решаемой задачи.

Теория криволинейной корреляции решает те же задачи, что и теория линейной корреляции (установление формы и тесноты корреляционной связи). Неизвестные параметры уравнения регрессии ищут методом наименьших квадратов. Для оценки тесноты криволинейной корреляции служат выборочные корреляционные отношения (см. § 11).

Чтобы выяснить суть дела, ограничимся параболической корреляцией второго порядка, предположив, что данные n наблюдений (выборки) позволяют считать, что имеет место именно такая корреляция. В этом случае выборочное уравнение регрессии Y на Х имеет вид

=Ах²+Вх+С, (*)

где А, В, С—неизвестные параметры.

Пользуясь методом наименьших квадратов, получают систему линейных уравнений относительно неизвестных параметров (вывод опущен, поскольку он не содержит ничего нового сравнительно с § 4):

(**)

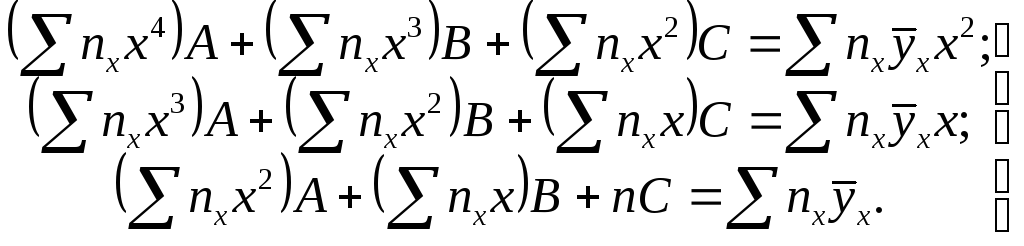Найденные из этой системы параметры А, В, С подставляют в (*); в итоге получают искомое уравнение регрессии.

Пример. Найти выборочное уравнение регрессии Y на Х вида =Ах²+Вх+С по данным корреляционной табл. 19.

Таблица 19

Y	х
	1	1,1	1.2	ny
6	8	2	—	10
7	—	30	—	30
7,5	—	1	9	10
nx	8	33	9	n=50
	6	6,73	7.5

Составим расчетную табл. 20. Подставив числа (суммы) нижней строки табл. 20 в (**), получим систему

Решив эту систему, найдем: Л =1,94, В =2,98, С ==1,10. Напишем искомое уравнение регрессии:

=1,94х²+2,98х+1,10.

Легко убедиться, что условные средние, вычисленные по этому уравнению, незначительно отличаются от условных средних корреляционной таблицы. Например, при х₁=1 найдем: по таблице у₁= 6; по уравнению =1,94+2,98+1,10=6,02. Таким образом, найденное уравнение хорошо согласуется с данными наблюдений (выборки).