§ 4. Метод произведений для вычисления выборочных средней и дисперсии

Метод произведений дает удобный способ вычисления условных моментов различных порядков вариационного ряда с равноотстоящими вариантами. Зная же условные моменты, нетрудно найти интересующие нас начальные и центральные эмпирические моменты. В частности, методом произведений удобно вычислять выборочную среднюю и выборочную дисперсию. Целесообразно пользоваться расчетной таблицей, которая составляется так:

1. в первый столбец таблицы записывают выборочные (первоначальные) варианты, располагая их в возрастающем порядке;

2. во второй столбец записывают частоты вариант; складывают все частоты и их сумму (объем выборки n) помещают в нижнюю клетку столбца;

3. в третий столбец записывают условные варианты u_i = (x_i - C)/h, причем в качестве ложного нуля С выбирают варианту, которая расположена примерно в середине вариационного ряда, и полагают h равным разности между любыми двумя соседними вариантами; практически же третий столбец заполняется так: в клетке строки, содержащей выбранный ложный нуль, пишут 0; в клетках над нулем пишут последовательно —1, —2, —3 и т.д., а под нулем—1, 2, 3 и т.д.;

4. умножают частоты на условные варианты и записывают их произведения n_iu_i - в четвертый столбец; сложив все полученные числа, их сумму 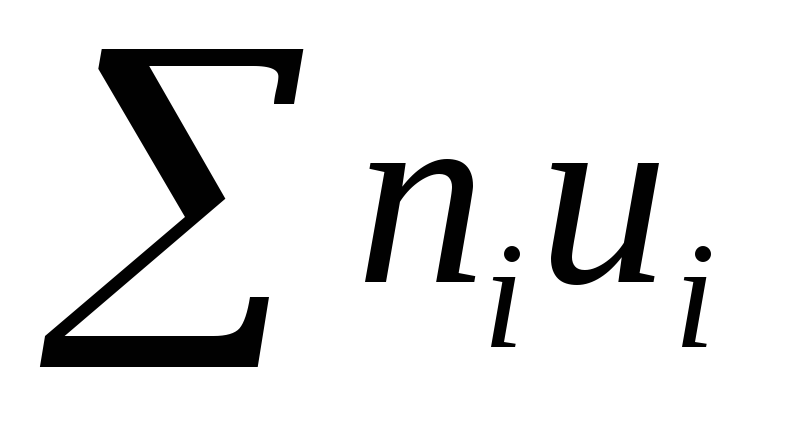помещают в нижнюю клетку столбца;

5. умножают частоты на квадраты условных вариант и записывают их произведения n_iu_i² в пятый столбец; сложив все полученные числа, их сумму 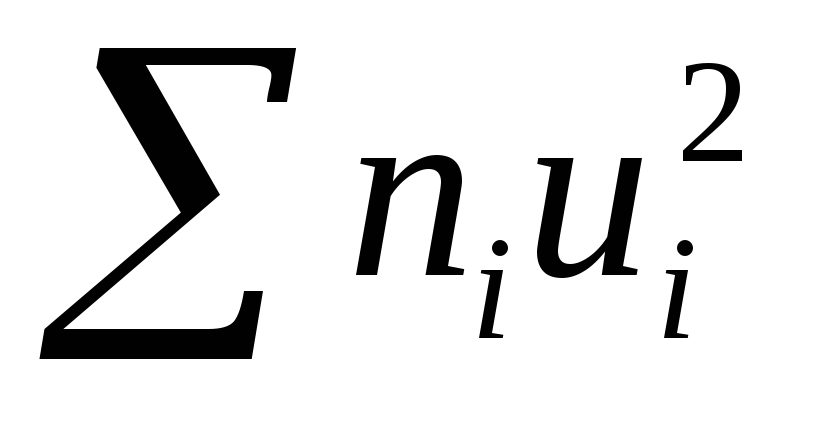помещают в нижнюю клетку столбца;

6. умножают частоты на квадраты условных вариант,увеличенных каждая на единицу, и записывают произведения n_i (u_i+1)² в шестой контрольный столбец; сложив все полученные числа, их сумму 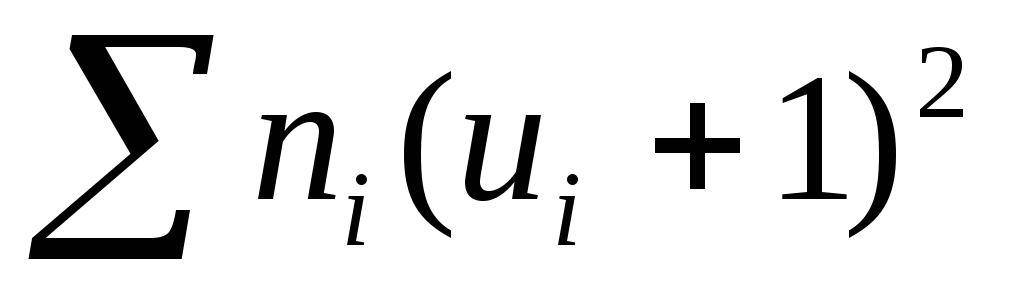помещают в нижнюю клетку столбца.

Замечание 1. Целесообразно отдельно складывать отрицательные числа четвертого столбца (их сумму A₁ записывают в клетку строки, содержащей ложный нуль) и отдельно положительные

числа (их сумму A₂ записывают в предпоследнюю клетку столбца); тогда .

Замечание 2. При вычислении произведений n_iu_i² пятого столбца целесообразно числа n_iu_i четвертого столбца умножать на u_i.

Замечание 3. Шестой столбец служит для контроля вычислений: если сумма окажется равной сумме (как и должно быть в соответствии с тождеством )то вычисления проведены правильно.

После того как расчетная таблица заполнена и проверена правильность вычислений, вычисляют условные моменты:

, .

Наконец, вычисляют выборочные среднюю и дисперсию по формулам (*) и (****) § 3:

, .

Пример. Найти методом произведений выборочные среднюю и дисперсию следующего статистического распределения:

варианты 10,2 10,4 10,6 10,8 11,0 11,2 11,4 11,6 11,8 12,0

частоты 2 3 8 13 25 20 12 10 6 1

Решение. Составим расчетную таблицу, для чего:

1. запишем варианты в первый столбец;

2. запишем частоты во второй столбец; сумму частот (100) поместим в нижнюю клетку столбца;

3. в качестве ложного нуля выберем варианту 11,0 (эта варианта расположена примерно в середине вариационного ряда); в клетке третьего столбца, которая принадлежит строке, содержащей выбранный ложный нуль, пишем 0; над нулем записываем последовательно—1, —2, —3, —4, а под нулем — 1 , 2, 3, 4, 5;

4. произведения частот на условные варианты записываем в четвертый столбец; отдельно находим сумму ( — 46) отрицательных и отдельно сумму (103) положительных чисел; сложив эти числа, их сумму (57) помещаем в нижнюю клетку столбца;

5. произведения частот на квадраты условных вариант запишем в пятый столбец; сумму чисел столбца (383) помещаем в нижнюю клетку столбца;

6. произведения частот на квадраты условных вариант, увеличенных на единицу, запишем в шестой контрольный столбец; сумму (597) чисел столбца помещаем в нижнюю клетку столбца.

В итоге получим расчетную табл. 7.

Контроль: =383+2*57+100= 597.

.

Вычисления произведены правильно.

Таблица 7

1	2	3	4	5	6
xi	ni	ui	niui	niui2	ni (ui+1)2
10,2	2	-4	-8	32	18
10,4	3	-3	-9	27	12
10,6	8	-2	-16	32	8
10,8	13	-1	-13	13	0
11,0	25	0	A1=-46		25
11,2	20	1	20	20	80
11,4	12	2	24	48	108
11,6	10	3	30	90	160
11,8	6	4	24	96	150
12,0	1	5	5	25	36
		A2=103
	n=100		=57	=383	=597

Вычислим условные моменты первого и второго порядков:

= 57/ 100 = 0,57;

= 383/ 100 = 3,83.

Найдем шаг: h= 10,4— 10,2 = 0,2.

Вычислим искомые выборочные среднюю и дисперсию:

= 0,57 *0,2 + 11,0 = 11,1 ;

= [3,83 — (0,57)²]*0,2² = 0,14.