§ 23. Другие характеристики вариационного ряда

Кроме выборочной средней и выборочной дисперсии применяются и другие характеристики вариационного ряда. Укажем главные из них.

Модой М₀ называют варианту, которая имеет наибольшую частоту. Например, для ряда

варианта ....1 4 7 9

частота .... 5 1 20 6

мода равна 7.

Медианой т_е называют варианту, которая делит вариационный ряд на две части, равные по числу вариант. Если число вариант нечетно, т.е. n = 2k+ 1, то m_е=x_k+1 при четном n = 2k медиана

Например, для ряда 23567 медиана равна 5; для ряда 235679 медиана равна (5 + 6)/2 = 5,5.

Размахом варьирования R называют разность между наибольшей и наименьшей вариантами:

R=x_max-x_min

Например, для ряда 1 3456 10 размах равен 10 — 1 =9.

Размах является простейшей характеристикой рассеяния вариационного ряда.

Средним абсолютным отклонением θ называют среднее арифметическое абсолютных отклонений:

Например, для ряда

х_i 1 3 6 16

n_i 4 10 5 1

имеем:

;

Среднее абсолютное отклонение служит для характеристики рассеяния вариационного ряда.

Коэффициентом вариации V называют выраженное в процентах отношение выборочного среднего квадратического отклонения к выборочной средней:

.

Коэффициент вариации служит для сравнения величин рассеяния по отношению к выборочной средней двух вариационных рядов: тот из рядов имеет большее рассеяние по отношению к выборочной средней, у которого коэффициент вариации больше. Коэффициент вариации — безразмерная величина, поэтому он пригоден для сравнения рассеяний вариационных рядов, варианты которых имеют различную размерность, например если варианты одного ряда выражены в сантиметрах, а другого — в граммах.

Замечание. Выше предполагалось, что вариационный ряд составлен по данным выборки, поэтому все описанные характеристики называют выборочными; если вариационный ряд составлен по данным генеральной совокупности, то характеристики называют генеральными.

Задачи

1. Найти групповые средние совокупности, состоящей из двух групп:

первая группа . . . Х{ 0,1 0,4 0,6

ni 325

вторая группа . . . */ 0,1 0,3 0,4 П{ 10 4 6

Отв. = 0,41; = 0,23.

2. Найти общую среднюю по данным задачи 1 двумя способами: а) объединить обе группы в одну совокупность; б) использовать найденные в задаче 1 групповые средние.

Отв. =0,29.

3. Дано распределение статистической совокупности:

х_i 1 4 5

п_i 6 11 3

Убедиться, что сумма произведений отклонений на соответствующие частоты равна нулю.

4. Дано распределение статистической совокупности:

x_i 4 7 10 15

п_i 10 15 20 5

Найти дисперсию совокупности: _а) исходя из определения дисперсии; б) пользуясь формулой D = —[].

Отв. D = 9,84.

б. Найти внутригрупповую, межгрупповую и общую дисперсии совокупности, состоящей из трех групп:

первая группа . . . Х{ 1 2 8

я/ 30 15 5

вторая группа ...*/..! 6

П{ 10 15

третья группа . . . */ 3 8

я,- 20 5

Отв. D_внгр = 4,6; D_межгр=1; D_общ = 5,6.

6. Найти внутригрупповую, межгрупповую и общую дисперсии совокупности, состоящей из двух групп:

первая группа . . . Х{ 2 7

П( 64

вторая группа . . . х,- 2 7

л/28

Отв. D_внгр = ; D_межгр=1; D_общ = 6.

7. Найти выборочную и исправленную дисперсии вариационного ряда, составленного по данным выборкам:

варианта ... 1 2 5 8 9

частота ... 3 4 6 4 3

Отв: = 8,4; s² = 8,84.

В задачах 8—9 даны среднее квадратическое отклонение, выборочная средняя и объем выборки нормально распределенного признака. Найти доверительные интервалы для оценки неизвестного математического ожидания с заданной надежностью.

8. σ = 2, 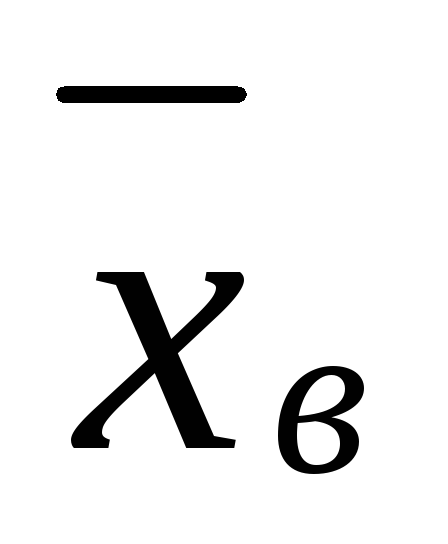= 5,40, n = 10, γ = 0,95. Отв. 4,16_< а < 6,64.

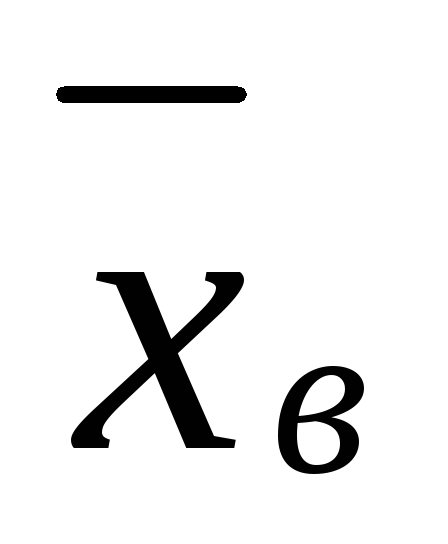9. σ = 3, = 20,12, n = 25, γ = 0,99. Отв. 18,57 < а < 21,67.

10. Найти минимальный объем выборки, при котором с надежностью 0,95 точность оценки математического ожидания нормально распределенного признака по выборочной средней будет равна 0,2, если среднее квадратическое отклонение равно 2.

Указание. См. замечание 2, § 15.

Отв. n = 385.

В задачах 11—12 даны «исправленное» среднее квадратическое отклонение, выборочная средняя и объем малой выборки нормально распределенного признака. Найти, пользуясь распределением Стью-

дента, доверительные интервалы для оценки неизвестного математического ожидания с заданной надежностью.

11. s = 1,5, =16,8, n = 12, γ = 0,95. Отв. 15,85 < a < 17,75.

12. s = 2,4, =14,2, n = 9, γ = 0,99. Отв. 11,512 < a < 16,888.

13. По данным 16 независимых равноточных измерений физической величины найдены = 23, 161 и s = 0,400. Требуется оценить истинное значение а измеряемой величины и точность измерений σ с надежностью 0,95.

Отв. 22,948 < а < 23,374; 0,224 < σ < 0,576.

14. Найти доверительный интервал для оценки неизвестной вероятности р биномиального распределения с надежностью 0,95, если в 60 испытаниях событие появилось 18 раз.

Отв. 0,200 < р < 0,424.

15. Найти методом моментов точечную оценку эксцесса Е_k =m₄/σ⁴ - 3 теоретического распределения.

Отв. е_k = m₄/σ⁴ – 3.

16. Найти методом моментов точечные оценки параметров α и β гамма-распределения

.

Указание. Сделать подстановку у = х/β и, используя гаммафункцию

, найти сначала М (X) = (α+ 1) β, D (Х) = (α+1) β², а затем приравнять М(Х)= , D(X) = D_в.

Отв. α* = (/D_в)— 1; β* = D_в/.

17. Найти методом наибольшего правдоподобия по выборке х₁, х₂, ..., х_п точечную оценку неизвестного параметра β гамма-распределения, если параметр α известен.

Указание. Использовать плотность гамма-распределения, приведенную в задаче 16.

Отв β* = /(α+1).

Глава семнадцатая

МЕТОДЫ РАСЧЕТА СВОДНЫХ ХАРАКТЕРИСТИК

ВЫБОРКИ