Федеральное агентство по образованию

^{_______________________________________________________________________________________________________}

ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ

ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

«МОСКОВСКИЙ ЭНЕРГЕТИЧЕСКИЙ ИНСТИТУТ

(ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ)»

филиал в г. Смоленске

Кратные интегралы

Методические указания

к типовому расчету по курсам

"Математика" и "Математический анализ"

Смоленск 2008

УДК 517.37

К 78

Утверждено учебно-методическим Советом филиала ГОУВПО «МЭИ(ТУ)» в

г. Смоленск в качестве методического пособия для студентов 1 курса

всех специальностей и 2 курса специальности

«Пищевая инженерия малых предприятий»

Рецензент:

Кандидат физико-математических наук, доцент СмолГУ Конашенко А.В.

Кратные интегралы:Методические указания к типовому расчету по курсам "Математика" и "Математический анализ" / Сост.: Борисов А.В., Новикова Т.Н. – Смоленск: филиал ГОУВПО «МЭИ(ТУ)», 2008 г. – 60 с.

Методические указания призваны помочь студентам при выполнении типового расчета по теме «Кратные интегралы». Они содержат необходимый теоретический материал и решения примеров, аналогичных примерам типового расчета по указанной теме. Пособие предназначено для студентов 1 курса всех специальностей и 2 курса специальности «Пищевая инженерия малых предприятий» при изучении курса высшей математики.

© Борисов А.В., Новикова Т.Н., 2008 г.

© Московский энергетический институт, филиал в г. Смоленске, 2008 г.

1. Двойные интегралы

1.1. Задача об объеме цилиндрического бруса

Точно так же, как задача о площади криволинейной трапеции привела нас к понятию простого определенного интеграла, аналогичная задача об объеме цилиндрического бруса приведет нас к новому понятию – двойного интеграла.

Рассмотрим тело (V), которое сверху ограничено поверхностью

z = f (x, y), (1.1)

cбоков - цилиндрической поверхностью с образующими, параллельными оси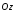, снизу – плоской фигурой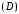на плоскости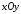(рис.1.1). Требуется найти объем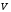тела.

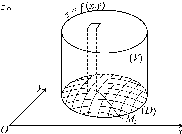
Рисунок. 1.1

Для решения этой задачи мы прибегнем к обычному в интегральном исчислении приему, состоящему в разложении искомой величины на элементарные части, приближенному подсчету каждой части, суммированию и последующему предельному переходу. С этой целью разобьем область 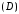сетью кривых на части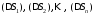и рассмотрим ряд цилиндрических столбиков, которые имеют своими основаниями эти частичные области и в совокупности составляют данное тело.

Для подсчета объема отдельных цилиндрических столбиков возьмем произвольно в каждой фигуре 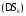по точкеM_k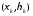. Если приближенно принять каждый столбик за цилиндр с высотой, равной аппликате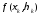, то объем отдельного столбика оказывается приближенно равным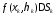, где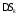означает площадь фигуры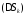.В таком случае приближенное выражение объема всего тела будет

.

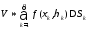Определение 1. Если взять любые пары точек в области то верхняя грань множества расстояний между ними называется диаметром области, обозначаетсяd.

Для повышения точности этого равенства будем уменьшать размеры площадок 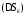, увеличивая их число. В пределе, при стремлении к нулю наибольшего из диаметровdвсех областей 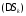, это равенство делается точным, так что

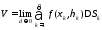, (1.2)

и поставленная задача решена.

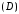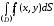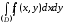Предел этого вида и есть двойной интеграл отфункции f (x,y) по области ; он обозначается символомили, так что формула (1.2) для объема принимает вид

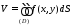. (1.2^*)

Таким образом, двойной интеграл является прямым обобщением понятия простого определенного интеграла на случай функции двух переменных.