Цифровая схемотехника

6. Построить схему дешифратора для 7-сегментного индикатора, отображающего не цифры, а буквы латинского алфавита: A, b, c, d, E, F, H, L, P, U. на двух дешифраторах 3-8 и элементах И-НЕ.

7.Составить таблицу истинности для приоритетного шифратора 8-3 с инверсными входами и выходами.

8.Построить схему шифратора 16-4 на двух шифраторах 8-3 с инверсными входами.

9.Построить схему шифратора 32-5 на шифраторах 8-3.

10.Построить схему преобразования кода Джонсона в двоичный код на дешифраторе и шифраторе.

11.Построить схему преобразования кода Грея в код Джонсона на дешифраторе и шифраторе.

4.3. Мультиплексоры и демультиплексоры

4.3.1. Мультиплексоры

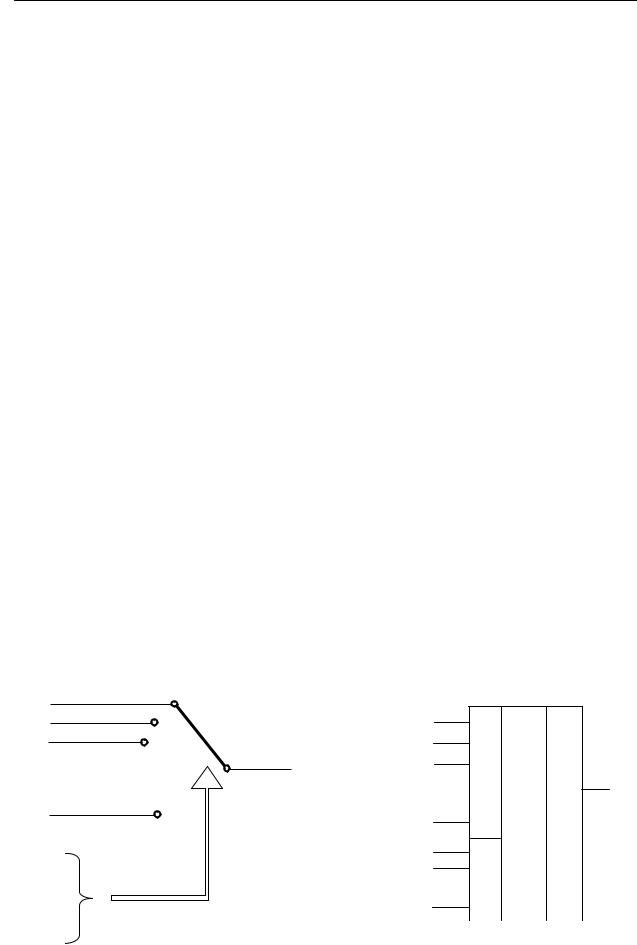
Мультиплексор – устройство, предназначенное для коммутации одного из нескольких входных сигналов на один выход. Мультиплексор является электронным аналогом механического переключателя, имеющего несколько входов и один выход (рис. 4.14а). Каждый из этих входов (обычно их обозначают D0 … Dn-1 и называют информационными входами) имеет свой номер (или адрес). Для выбора входного сигнала используются специальные адресные входы (a… ak-1), таким образом, с помощью k адресных входов можно выбрать один из n = 2k информационных входов и подключить его к выходу Q.

На рис. 4.14б приведено обозначение мультиплексора на схемах. Кроме информационных и адресных входов, мультиплексор может иметь прямой или инверсный вход разрешения (его обозначают V или C) и инверсный выход. Вместо надписи MUX в центральном поле прямоугольника может быть MS.

80

Комбинационные схемы

Мультиплексоры называют по числу имеющихся у них информационных входов. 2-входовый мультиплексор (рис. 4.15а) имеет один адресный вход. Если на него подан сигнал 0, то к выходу Q подключается вход D0 , а если 1 – вход D1 . В таблице истинности, описывающей работу мультиплексора, в столбцы аргументов обычно записывают адресные входы и вход разрешения, если он есть у данного мультиплексора, а в столбец выходной функции пишут имена входов, присоединенных при данном значении аргументов к выходу (табл. 4.11).

По таблице, описывающей работу мультиплексора, легко записать его функцию выхода:

В одной микросхеме обычно размещают четыре таких мультиплексора. Они имеют общий адресный вход, который обозначают Ā/B. Информационные входы тоже обозначают по-другому: входы D0 этих четырех мультиплексоров называют соответственно A1 A2 A3 A4, а входы D1 – B1 B2 B3 B4 (рис. 4.15б). Если на адресный вход Ā/B подать 0, то к выходу Qi (где i = 1 ÷ 4) подключается вход Ai , а если 1 – вход Bi (табл. 4.12). Мультиплексор имеет инверсный вход разрешения, т.е., чтобы на выходах появились нужные сигналы, на него необходимо подать сигнал 0.

4-входовый мультиплексор (рис. 4.16а) имеет два адресных входа. В одной микросхеме обычно размещают два таких мультиплексора (рис. 4.16б). Они имеют общие адресные входы, которые обозначают a0 и a1 (где a0 – младший адресный вход). Подавая на адресные входы различные сигналы, можно подключить к выходам соответствующие

81

Цифровая схемотехника

информационные входы (см. табл. 4.13). Оба мультиплексора имеют вход разрешения. Функцию выхода также легко записать:

Следующий по сложности – 8-входовый мультиплексор с тремя адресными входами (рис. 4.18). Если на вход разрешения подан сигнал 0, к выходу Q подключается один из информационных входов D0 D7 в зависимости от сигналов на адресных входах (табл. 4.14).

Рис. 4.17

По таблице истинности мультиплексора запишем функцию выхода с учетом входа разрешения:

82

Комбинационные схемы

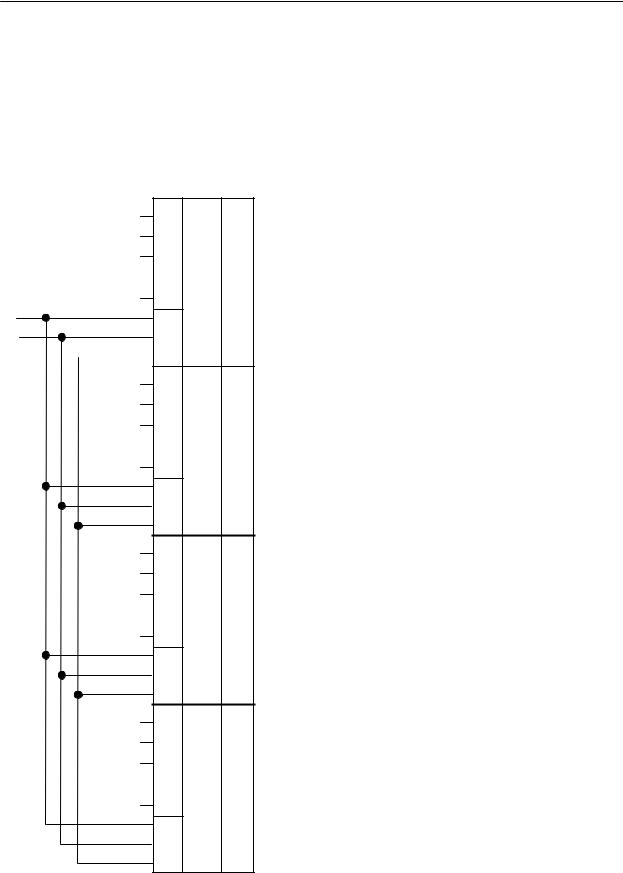
Мультиплексоры большего размера строятся чаще всего из описанных выше мультиплексоров меньшего размера. Например, для построения 32-входового мультиплексора нужно взять четыре 8- входовых и правильно скоммутировать их выходы (рис. 4.18).

Рис. 4.18

У 32-входового мультиплексора должно быть 5 адресных входов. Три из них, например, a0, a1, a2, подаем параллельно на адресные входы мультиплексоров D1 – D4, поэтому они будут работать синхронно.

83