1.1.2 Синтез 4-х шарнирного механизма

Синтез проводится по двум положениям выходного звена .

Составляется система уравнений из проекций векторного контура на оси координат:

; ;;;;;

Из решения системы (1.1), находится длина ДС звена 3

;

и длина ED звена 4

;

1.2 Выбор динамической модели

Объект динамического исследования представляет собой механизм, состоящий из 6 звеньев. Для того чтобы упростить определение закона движения такого механизма, реальный механизм заменяется динамической моделью. Модель представляет собой стойку и вращающееся звено 3, называемое звеном приведения, инерционность которого определяется суммарным приведенным моментом На звено приведения действует суммарный приведенный момент силПараметры динамической моделиопределены так, чтобы законы движения динамической модели и движения начального звена механизма совпадали.

1.3 Определение передаточных функций

Угол поворота звена 3:

Координаты точки В находятся из проекций векторного контура

(1.2)

Координаты точки D находятся из проекций векторного контура

(1.3)

Составляется система из проекций векторного контура на оси координат

;

(1.4)

Из решения системы (1.4), находится угол поворота звена 5

(1.5)

и угол поворота звена 4

(1.6)

Координаты точки Е находятся из проекций вектора

(1.7)

Координаты точки S7 находятся пропорциональным делением отрезка ОЕ

(1.8)

Передаточная угловая скорость определяется дифференцированием уравнения (1.5) по обобщенной координате

(1.9)

Передаточное отношение:

(1.10)

Передаточная скорость точки Е находится дифференцированием по обобщенной координате уравнения (1.7), которое определяет положение точки Е.

(1.11)

Передаточная скорость точки S7 находится пропорциональным делением:

(1.12)

Угол поворота звена 2 находится из векторного контура

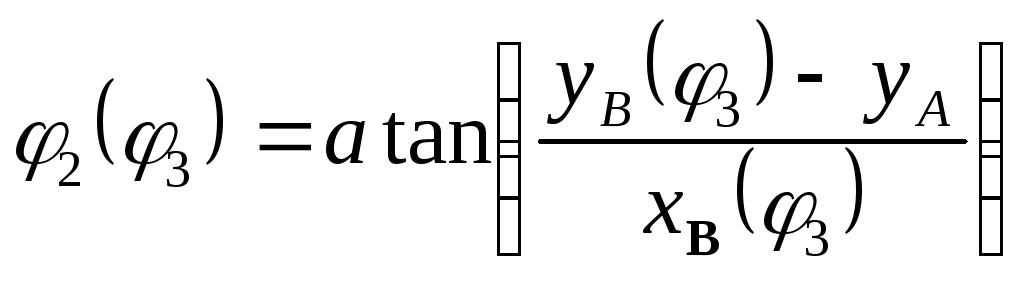(1.13)

Расстояние между шарнирами А и В определяется из векторного контура

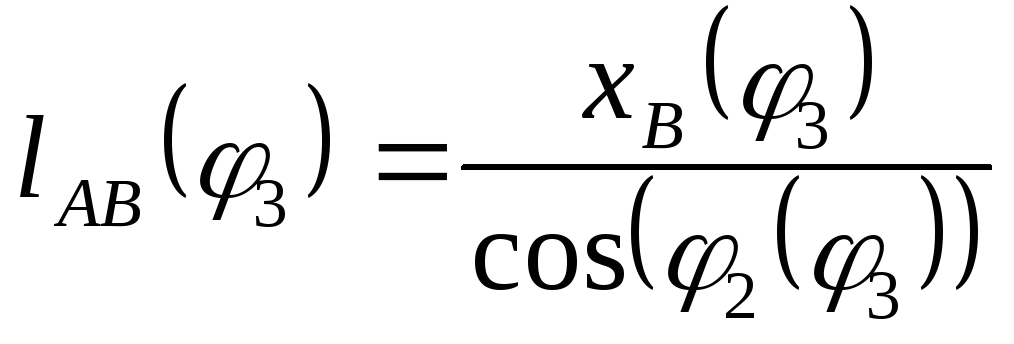(1.14)

Передаточная скорость движения поршня относительно цилиндра находится дифференцированием по обобщенной координате уравнения (1.14)

(1.15)

Перемещение поршня

(1.16)

Угол поворота звена 3

f=(0 0.18 0.4 0.6 0.77 1.0 1.047 1.2 1.4 1.57) i=0…9

Графики передаточных функций

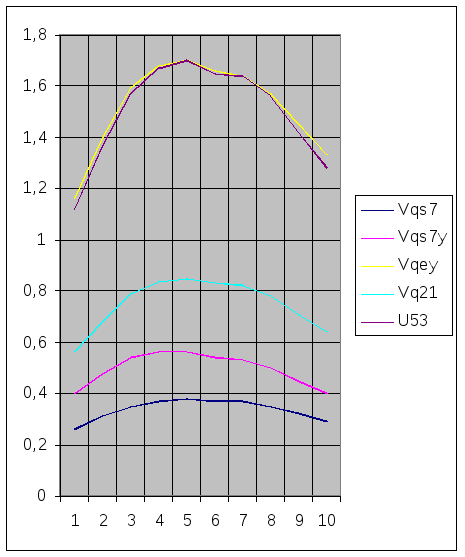
Таблица 1.1

0	0,26	0,4	1,16	0,56	1,12
0,18	0,31	0,48	1,4	0,68	1,37
0,4	0,35	0,54	1,59	0,79	1,57
0,6	0,37	0,56	1,68	0,84	1,67
0,77	0,38	0,56	1,7	0,85	1,7
1	0,37	0,54	1,66	0,83	1,65
1,05	0,37	0,53	1,64	0,82	1,64
1,2	0,35	0,5	1,57	0,78	1,56
1,4	0,32	0,45	1,45	0,71	1,42
1,57	0,29	0,4	1,33	0,64	1,28

1.4 Выбор закона движения механизма

Сила находится из условия начала движения.

Для получения безударной остановки определяются такие

При которых и

Ускорение свободного падения:

Сила тяжести действующая на звено 7:

Сила тяжести действующая на звено 5:

Сила тяжести действующая на звено 3:

Приведенный момент сил тяжести в начальный момент времени:

Приведенный момент движущей силы в начальный момент времени:

Сила определяется из условия начала движения механизма

т.е

Приведенный момент сил тяжести в конечный момент времени:

Приведенный момент движущей силы в конечный момент времени:

Определение из условия конца движения

т.е

Работа сил тяжести за время движения механизма

Работа движущей силы за время движения механизма

Определение из условия конца движения

т.е

Закон изменения движущей силы определяется методом линейной интерполяции:

Значения движущей силы в точках разрыва:

Значения перемещения поршня в точках разрыва:

Ход поршня:

График движущей силы

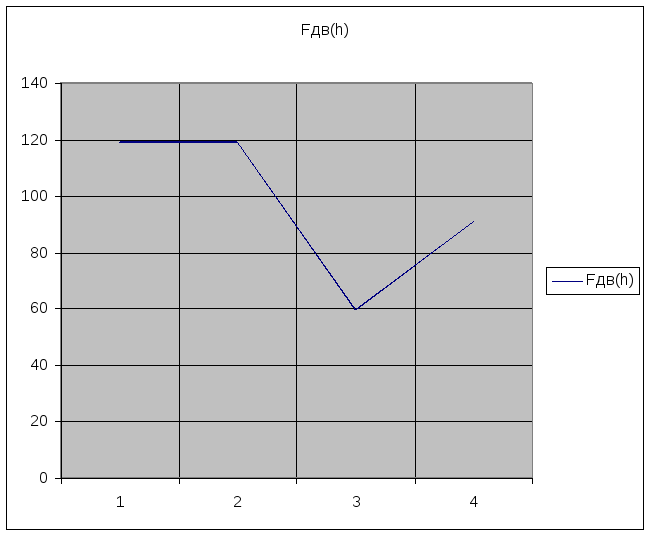
Рис. 1.2

Таблица 1.2

0	119,2
0,08	119,2
0,4	59,6
0,8	90,8

Зависимость движущей силы от обобщенной координаты

(1.17)