Интегралы с полиномами Эрмита
1. Вычисляем
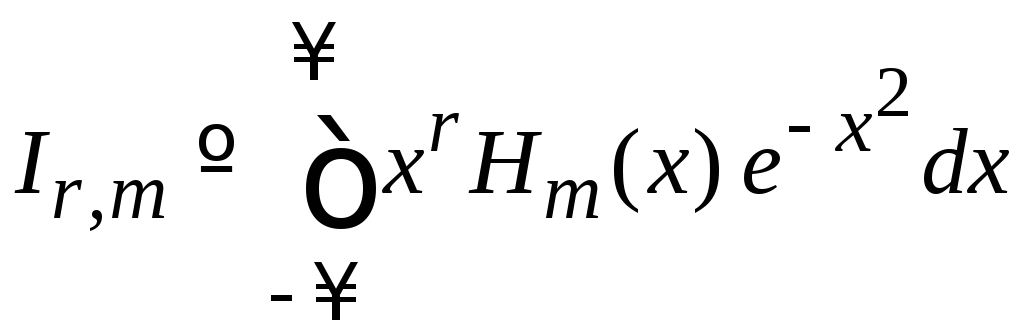
Учитываем четность
.
(6.3)
Если
–
нечетное,
тогда
.
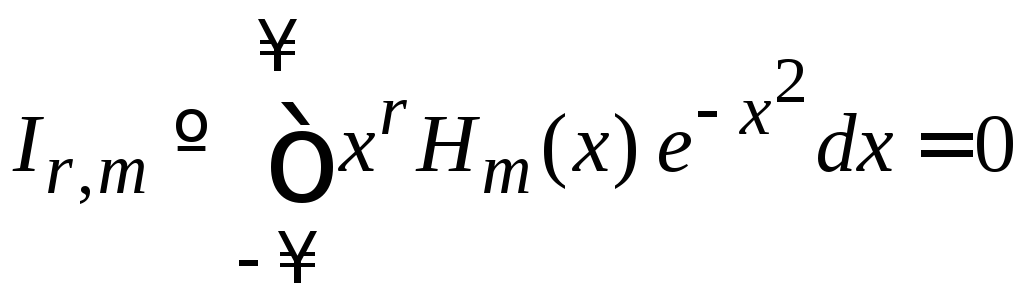Если
– четное,
то в
подставляем форму Родрига
.
(6.2)
Интегрируем по частям m раз, свободные слагаемые зануляются
=
.
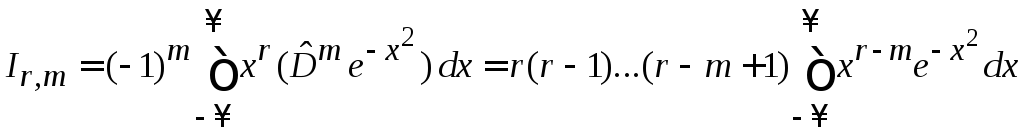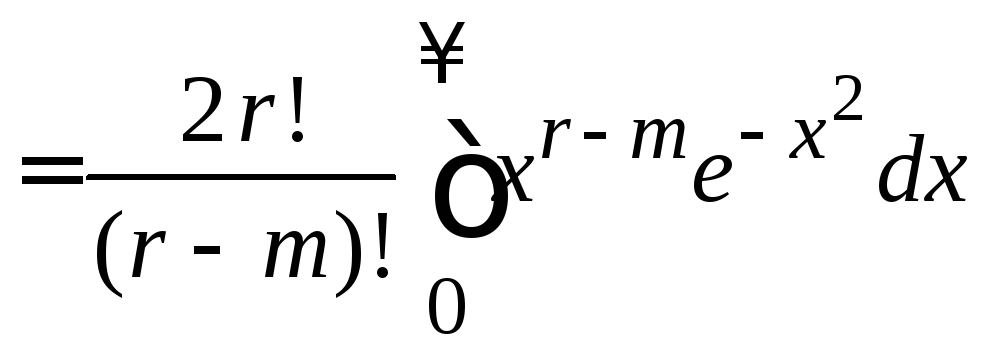Используем
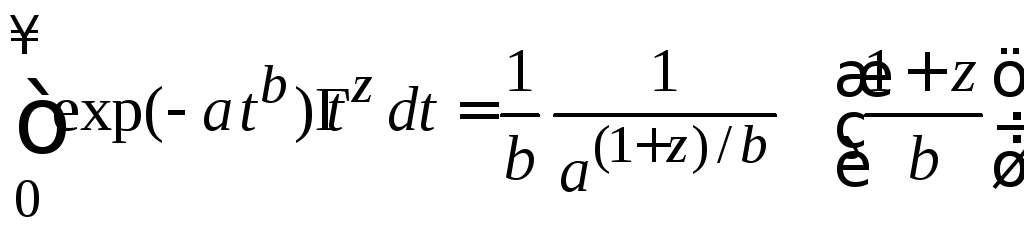(4.9)
при
,
,
и находим
.
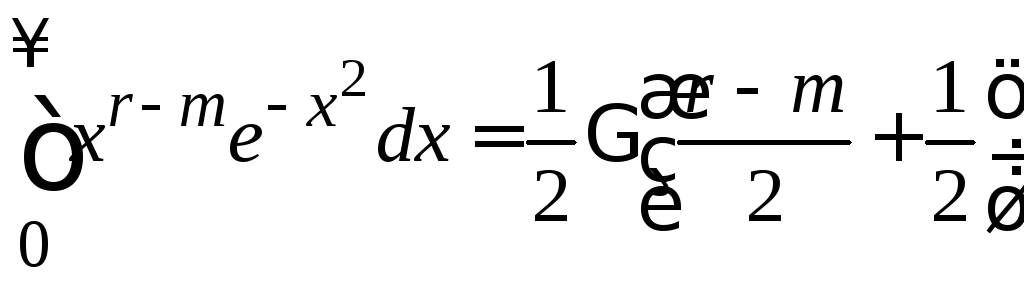Учитываем
,
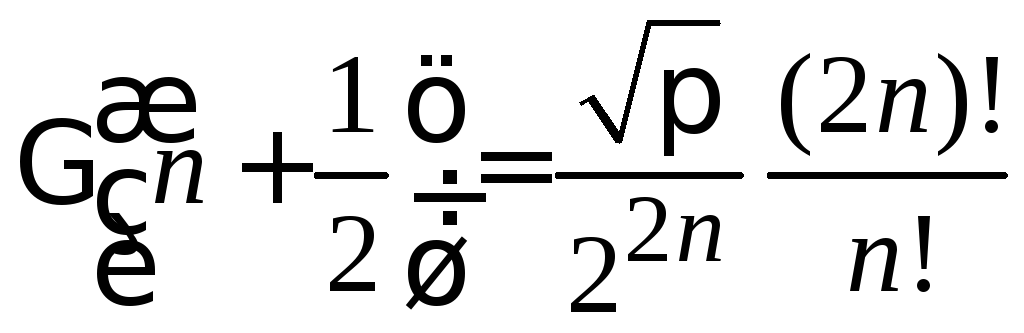(4.11)
тогда
.
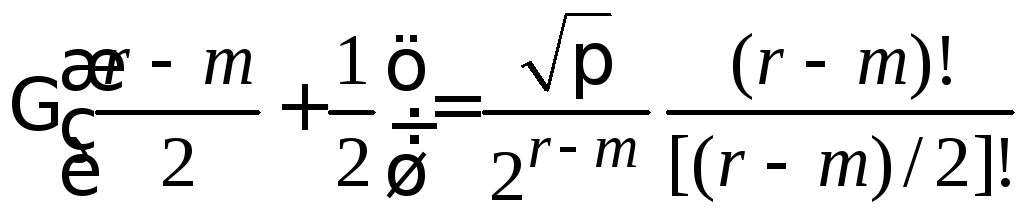В результате
,
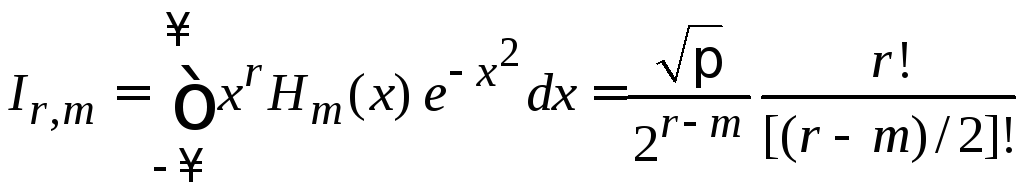– четное. (6.21)
Из
(6.21) при
с учетом
получаем
,
(6.21а)
Из
(6.21) при
,
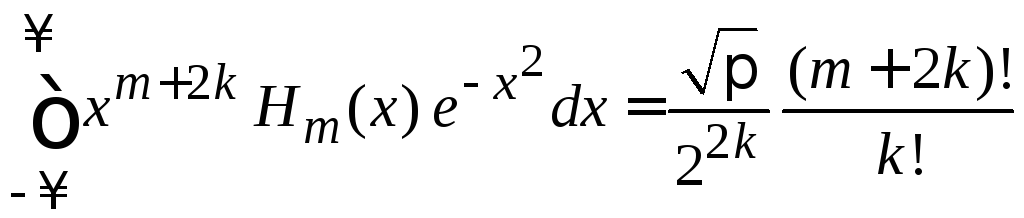(6.22)
Из
(6.22) при
и
находим
,
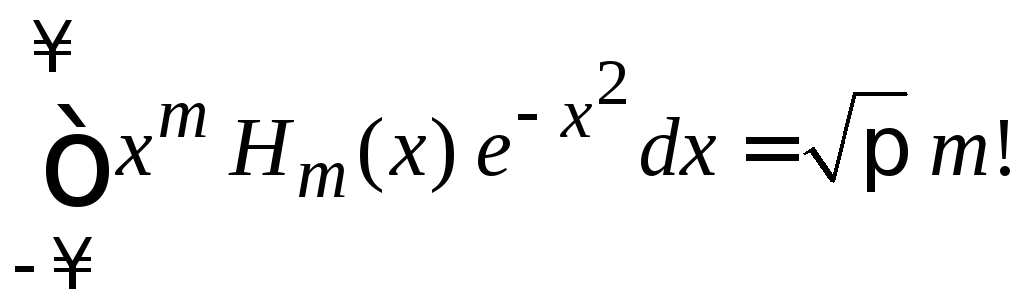(6.23)
.
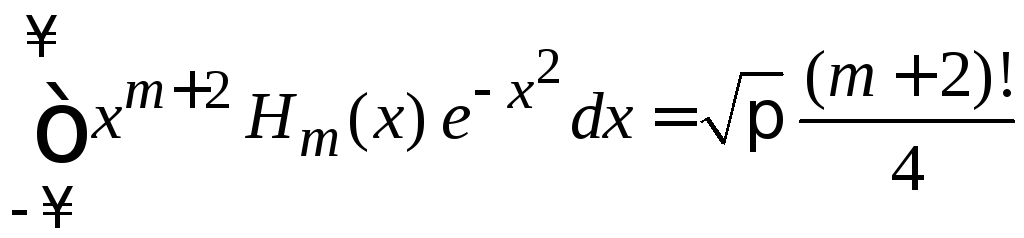(6.24)
В формуле
,
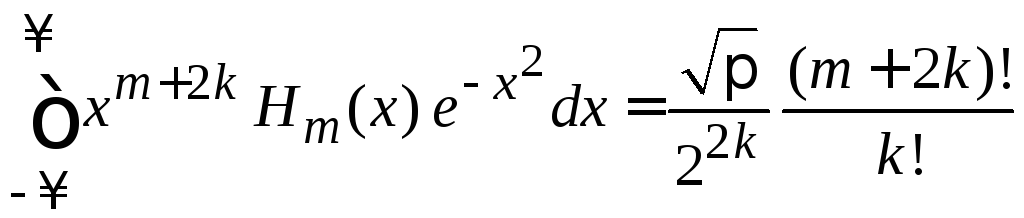(6.22)
заменяем
,
где
.
Преобразуем правую сторону (6.22)
.
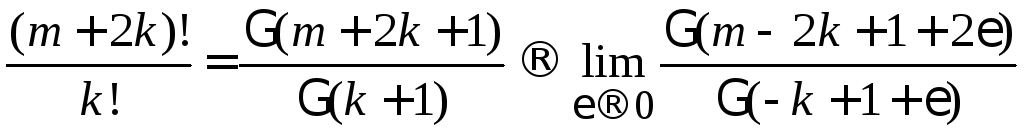Используем (4.4) в виде
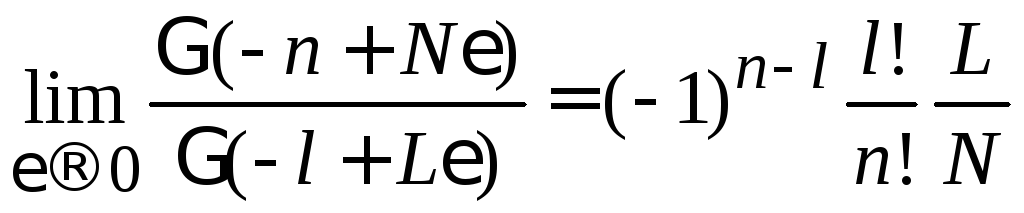
при
,
,
,
,
в результате
.
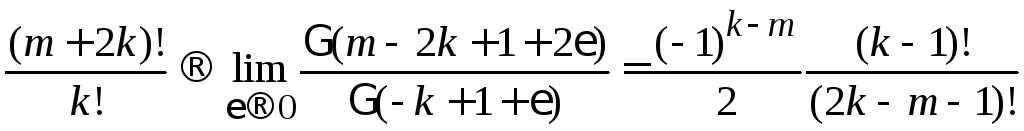В результате (6.22)
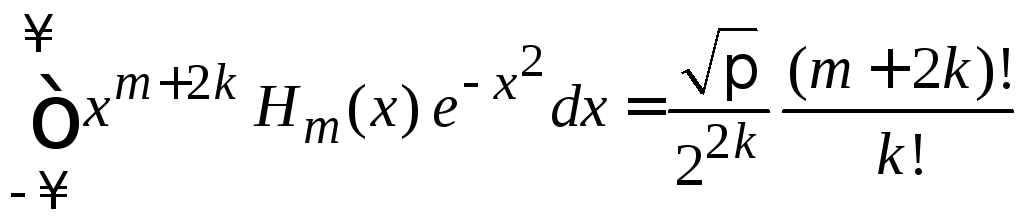
при
дает
,
.
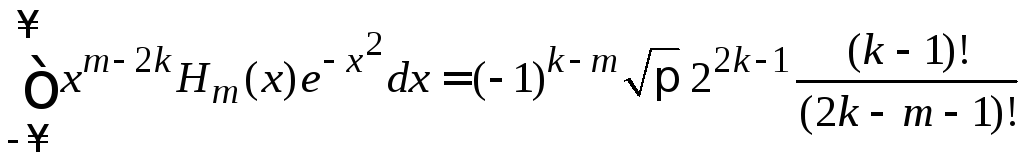(6.25)
Из
(6.25) при
и
получаем
,
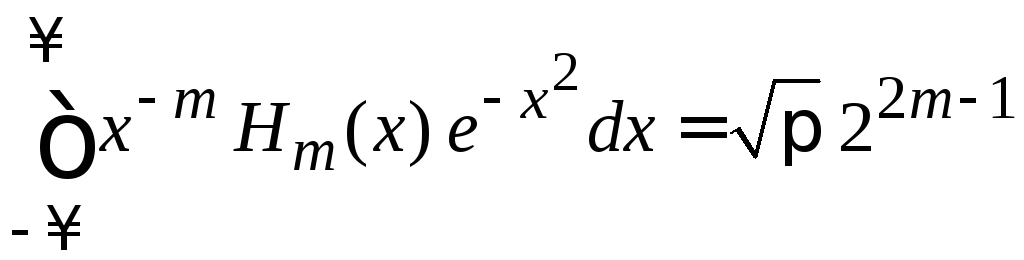(6.26)
.
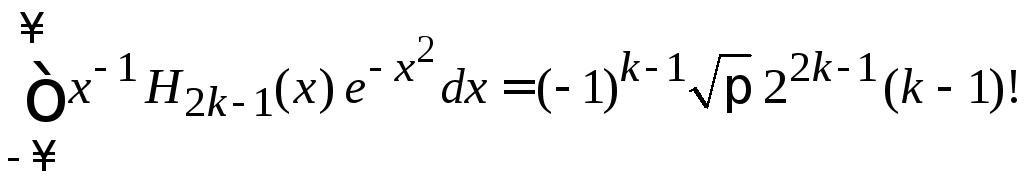(6.27)
2. Вычисляем
,
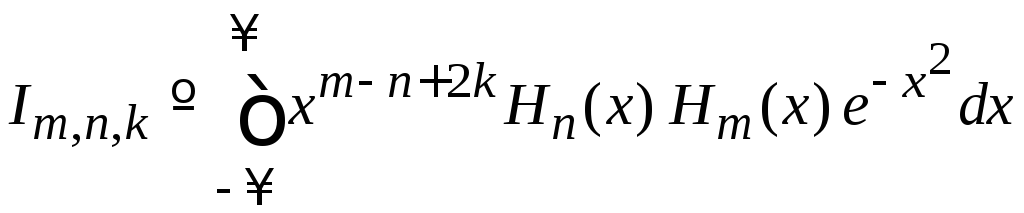Для
используем полиномиальную форму
,
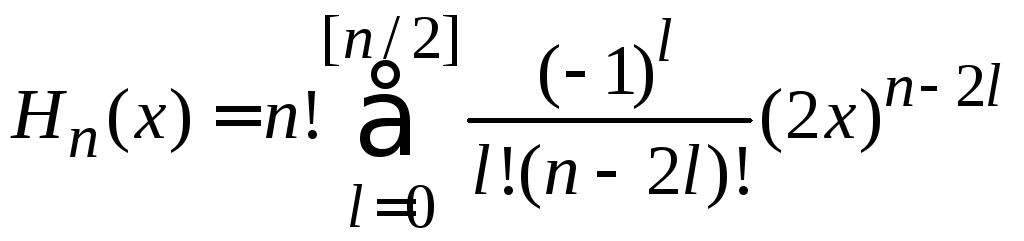(6.4)
тогда
.
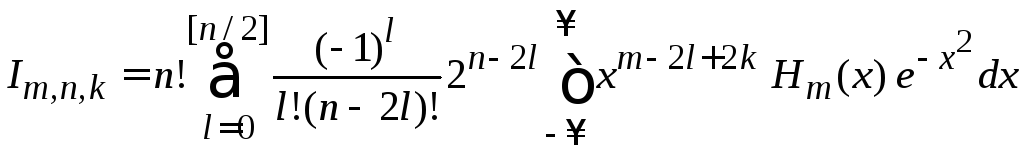Используем
,
,
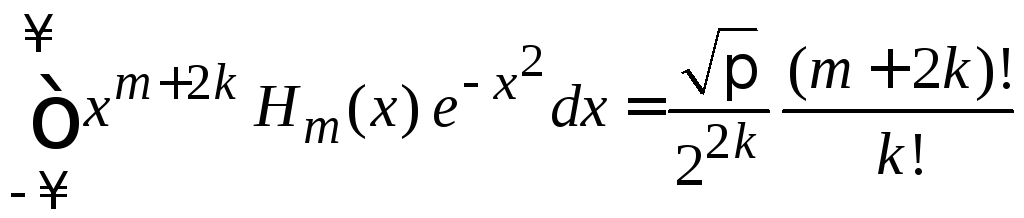(6.22)
при
.
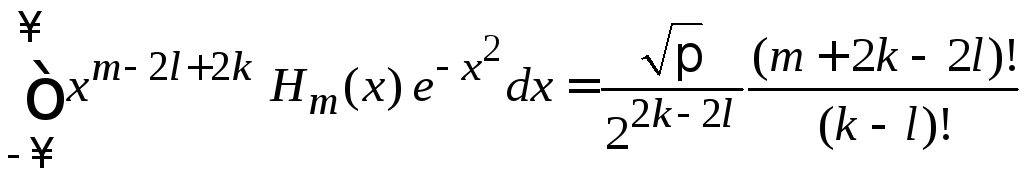В результате
=
,
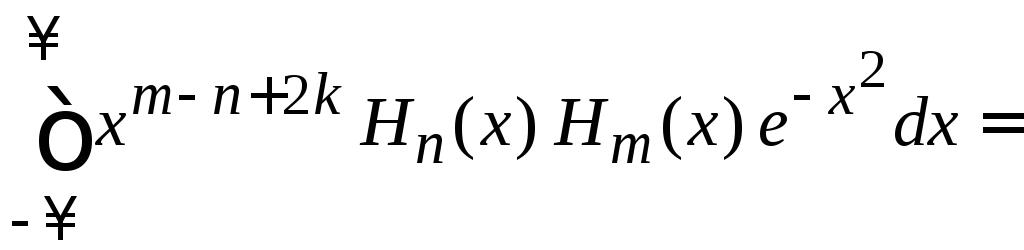
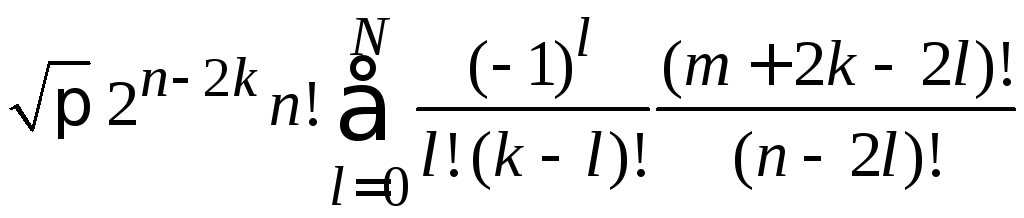(6.28)
где
знаменатели с факториалами ограничивают
.
При
,
из (6.28) получаем нормировку полиномов
Эрмита
.
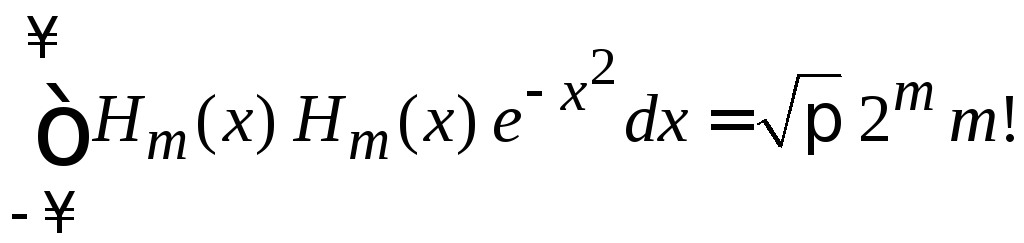(6.29)
При
,
и при
,
находим
,
.
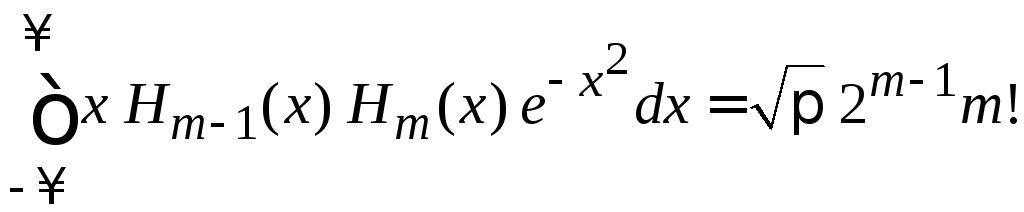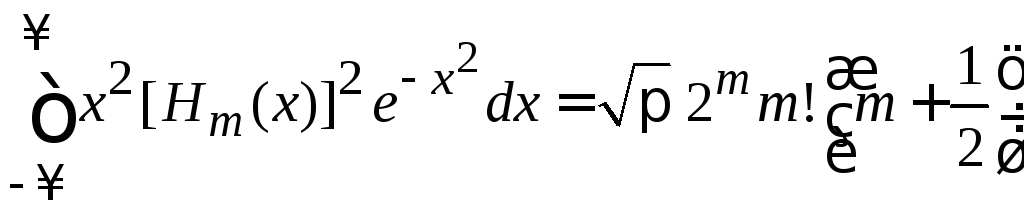Гармонический осциллятор
Система, колеблющаяся по гармоническому закону. От лат. oscillatio – «качание».
Осциллятор в классической теории
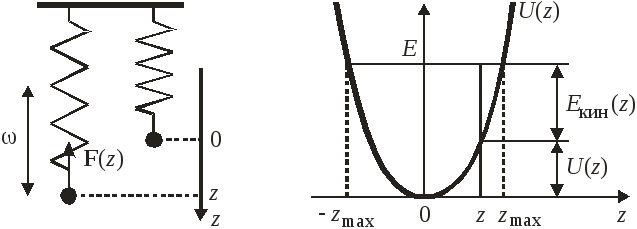
Масса µ находится в поле упругой потенциальной энергии
.
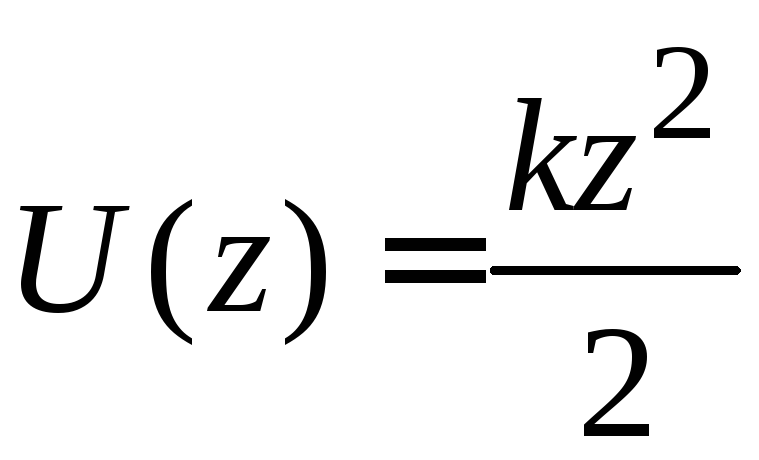Упругая сила
создает
ускорение
.
Второй закон Ньютона
дает уравнение Гельмгольца
,
где частота колебаний
,
,
тогда
.
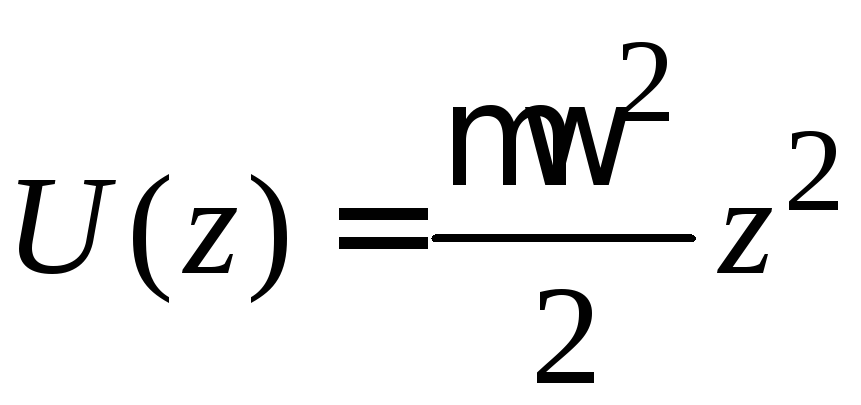Решение уравнения дает колебания
,
где
– амплитуда.
Полная энергия
.
При максимальном смещении
,
тогда
.
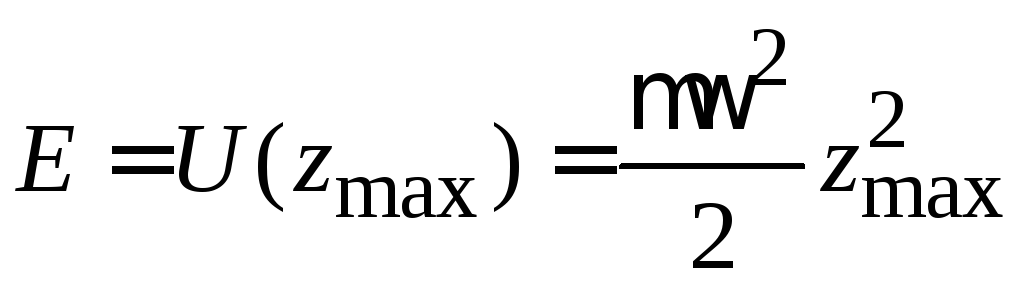Полная
энергия зависит от амплитуды колебаний
,
и может быть любой. Квадрат импульса
(6.30)
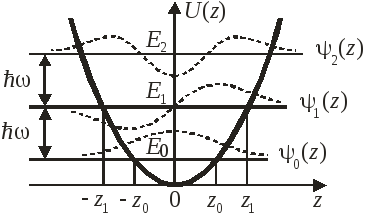
Осциллятор в квантовой теории
В квантовой теории спектр энергии эквидистантный
,
,
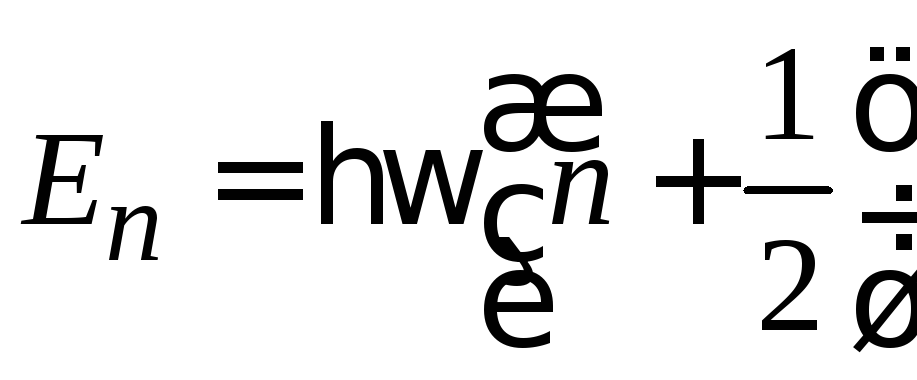уровню
n
сопоставляются n
квантов энергии
;
–энергия
вакуума.
Уравнение Шредингера
.
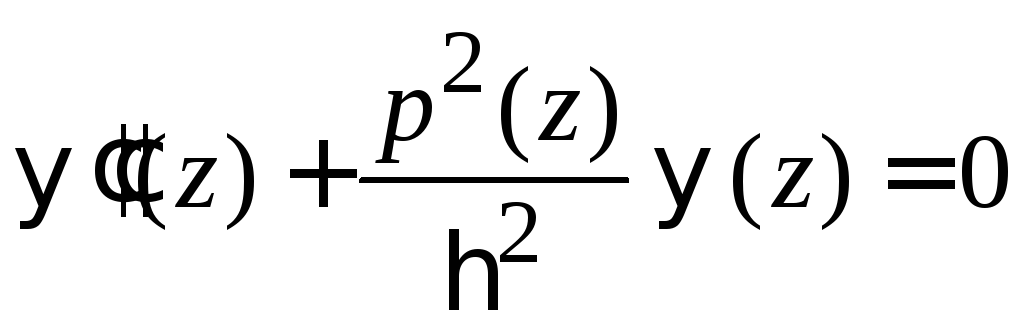Для осциллятора учитываем
,
(6.30)
получаем
для состояния
уравнение
.
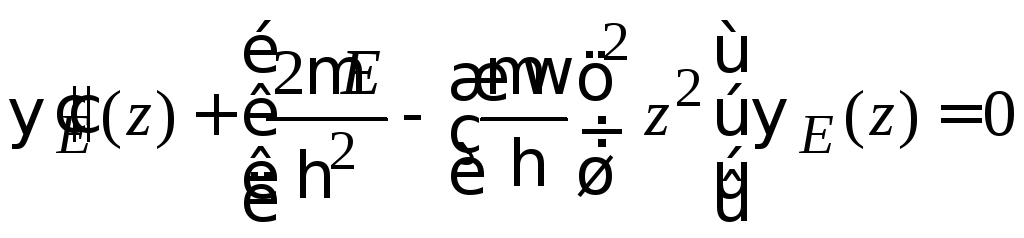Переходим к безразмерной координате
,
,
,
,
,
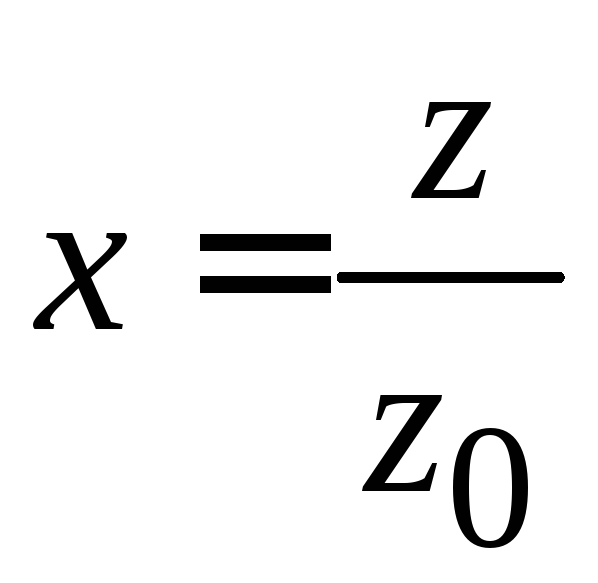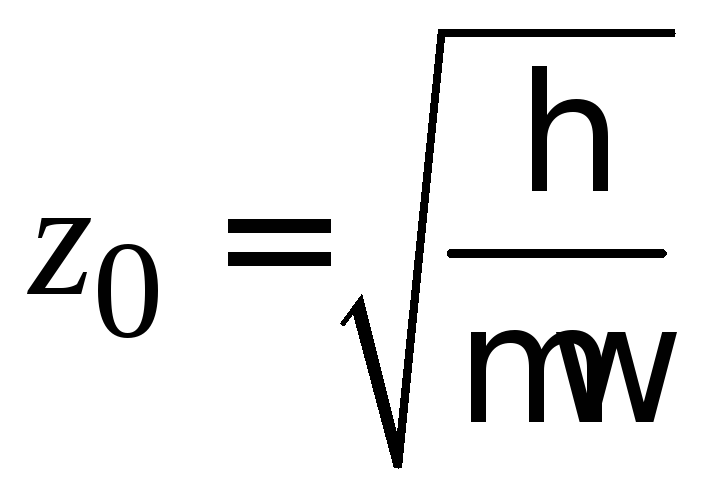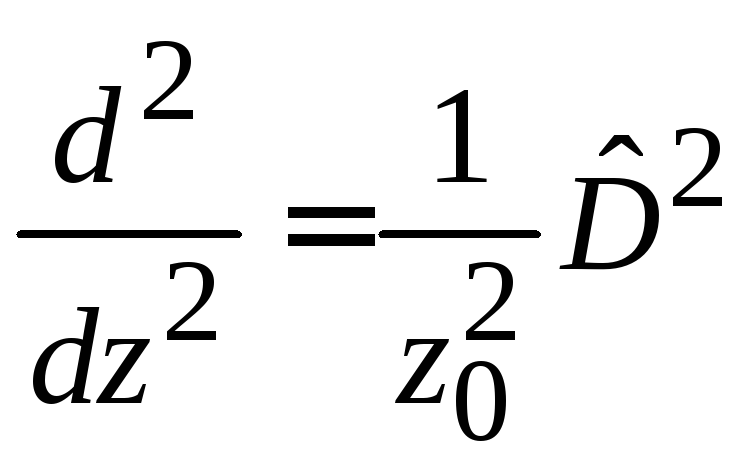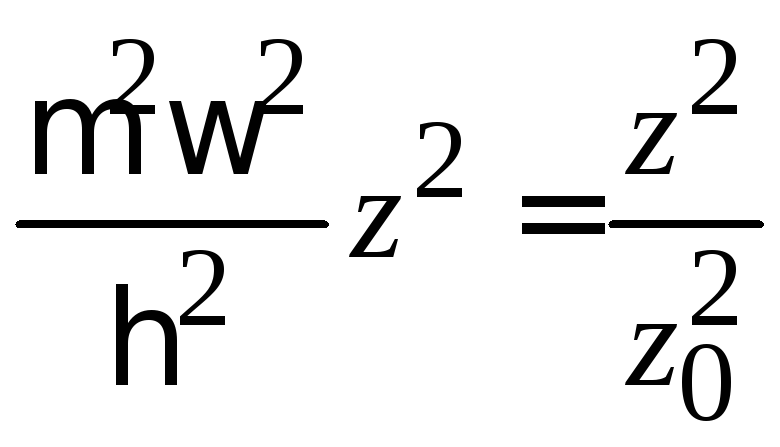Для
,
с учетом
,
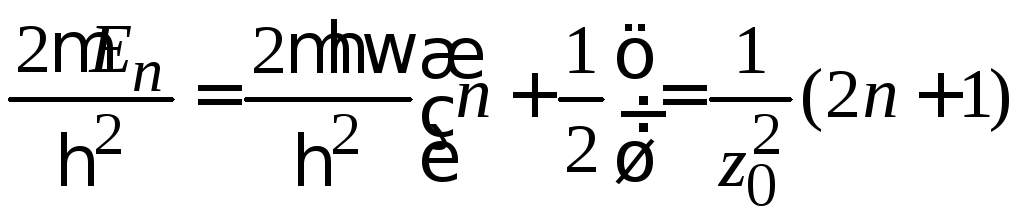получаем уравнение
,
(6.31)
Методом факторизации ранее получено решение (П.3.6) в виде функции Эрмита
.
(6.32)
Из (6.3)
и (6.32) находим
.
Условие ортонормированности
Из (П.3.7)
при
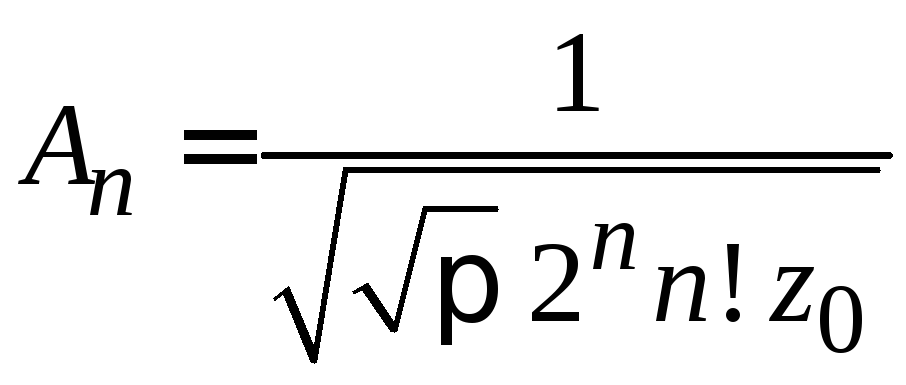
получаем
,
.
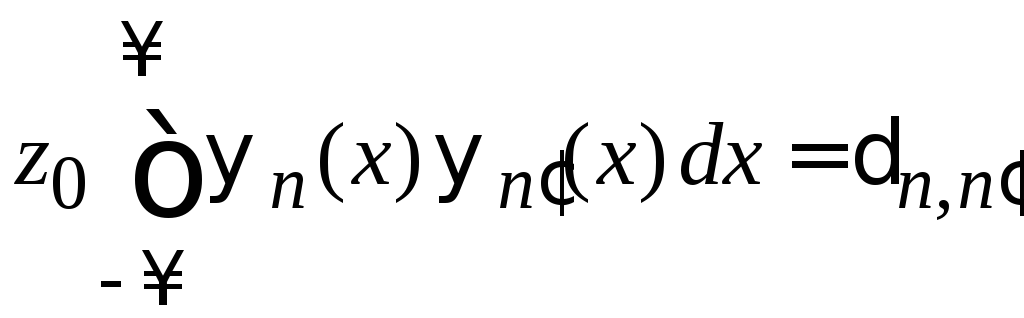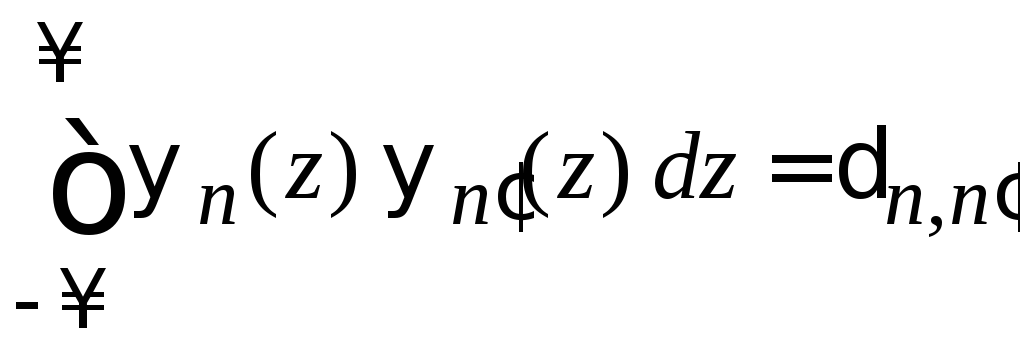(6.33)
Учитывая
,
,
,
из (6.32) находимосновное
состояние
,
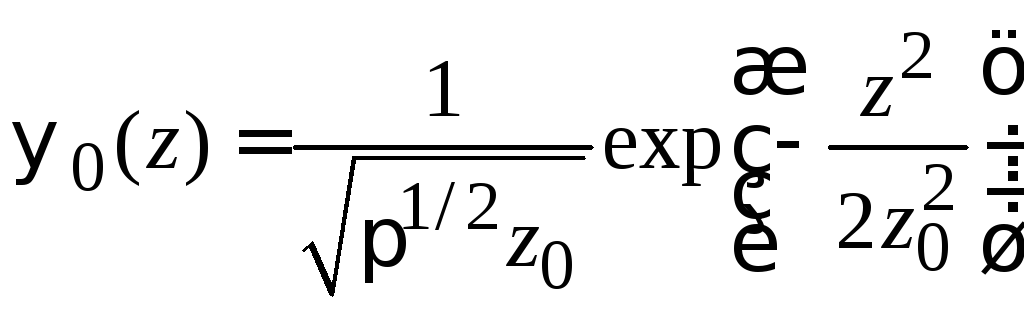(6.33а)
и первое возбужденное состояние
,
.
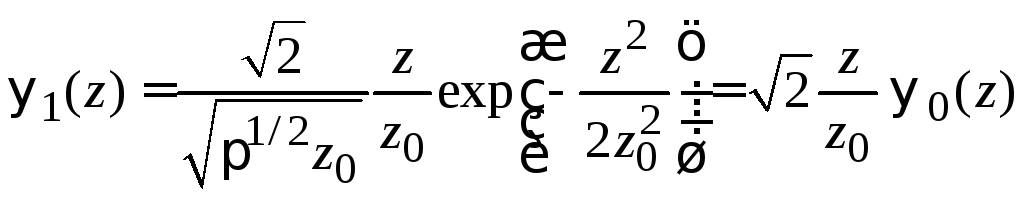(6.33б)
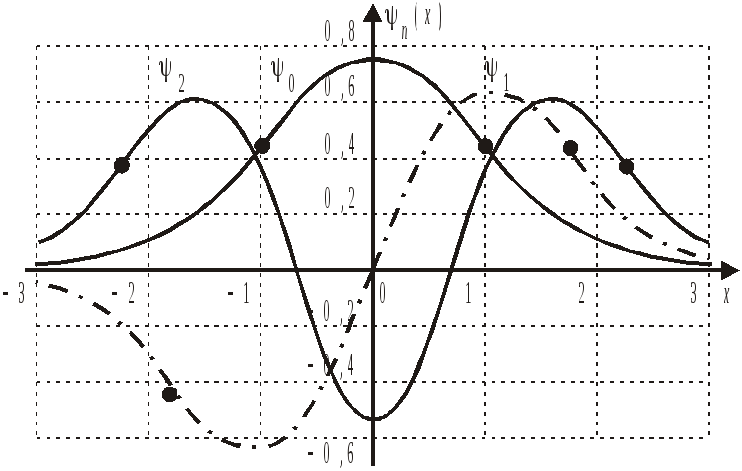
Точки поворота классического осциллятора
,
,
,
.
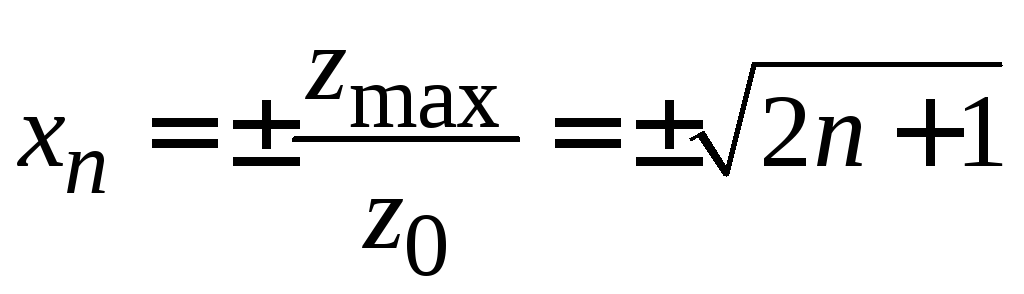Рекуррентные соотношения
Умножаем (6.15)
на
и учитываем
,
,
,
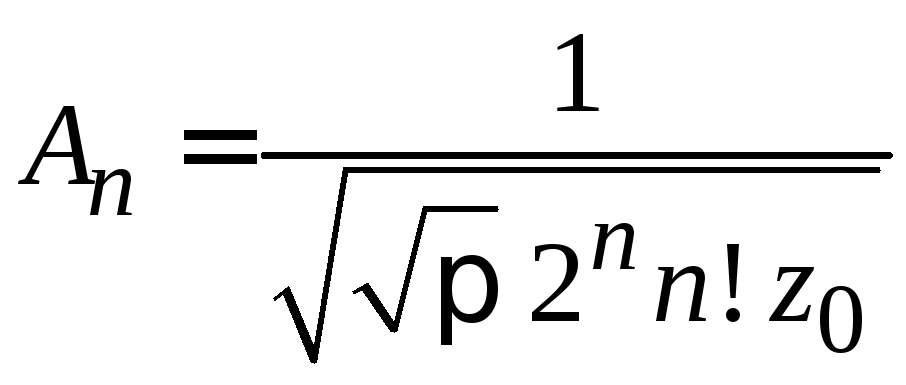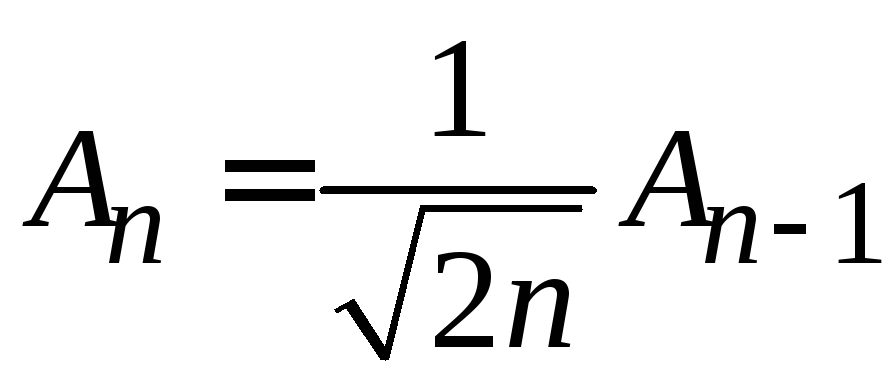для
.
(6.32)
находим
.
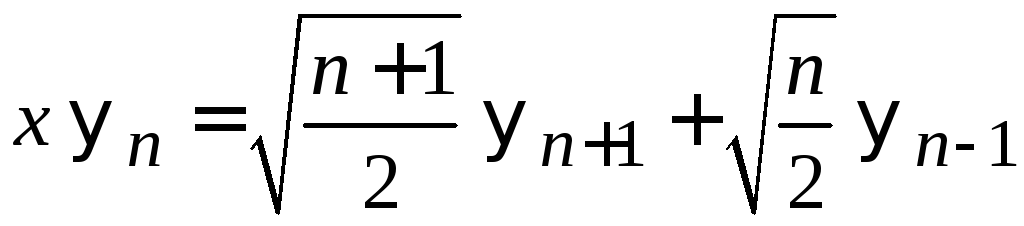(6.34)
Дифференцируем
,
(6.32)
.
Учитываем (6.12)
,
,
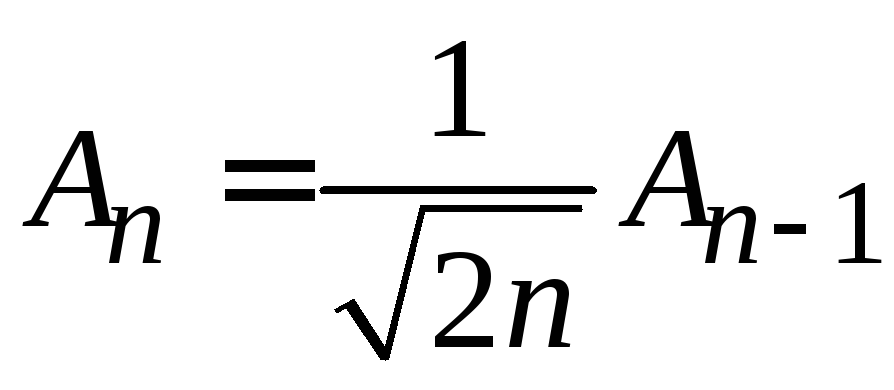получаем
.
(6.35)
Из (6.35)
.
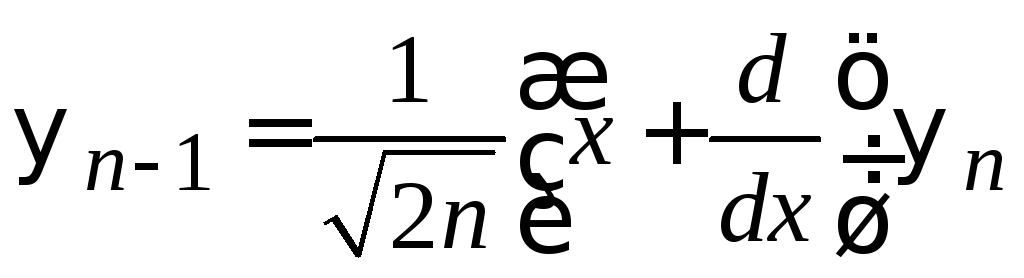(6.36)
Из
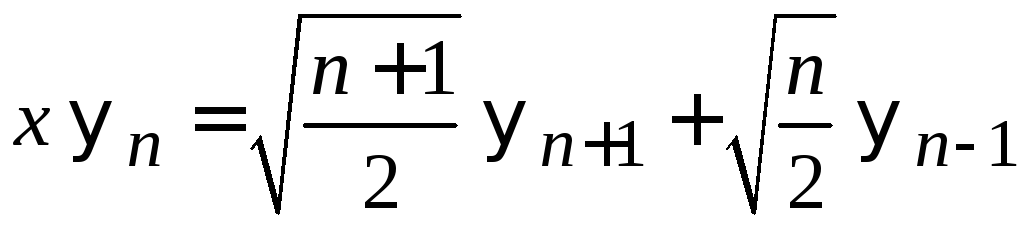(6.34)
выражаем
.
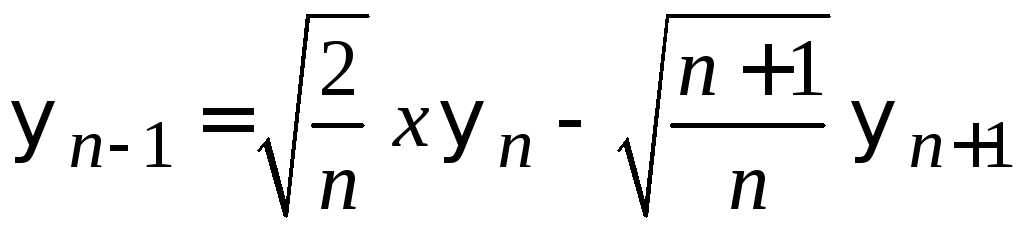Подстановка в (6.35) дает
.
(6.37)
Из (6.37) находим
.
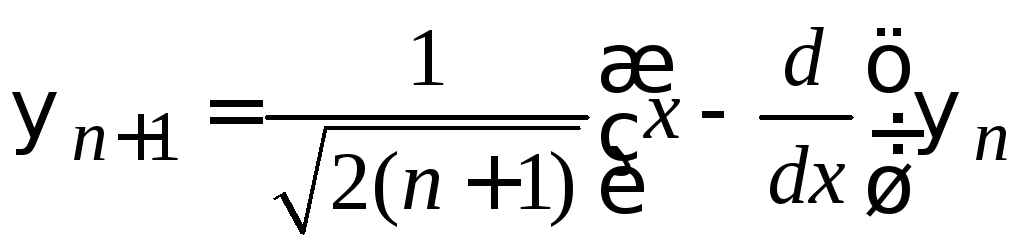(6.38)
Суммирование (6.35) и (6.37) дает
.
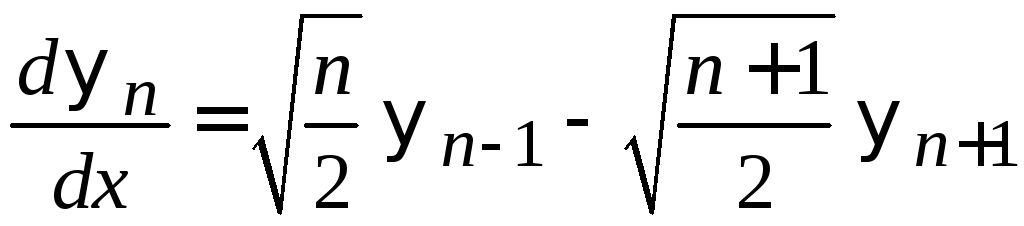(6.39)
Лестничные операторы
Изменяют состояние n на единицу
,
.
Из (6.36) и (6.38) получаем
,
.
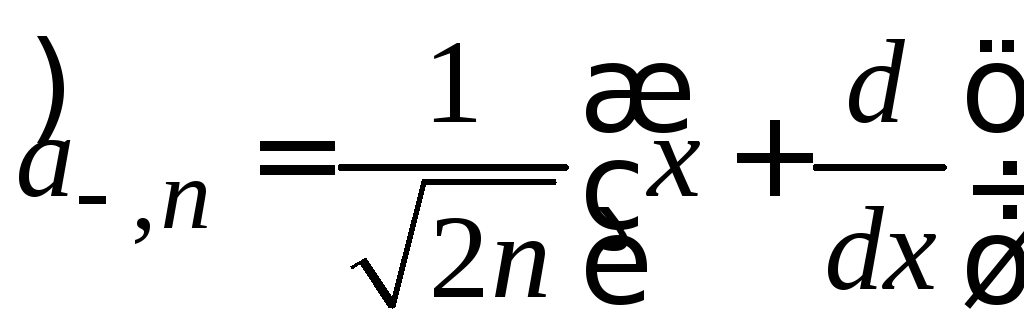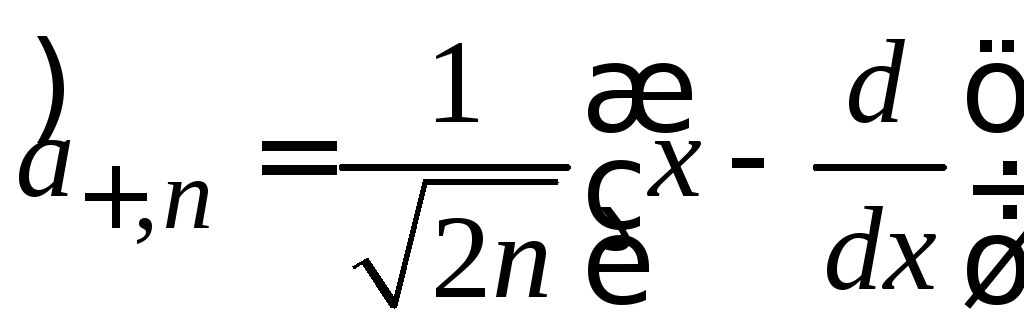(6.40)
Матричный элемент
Вероятность
перехода системы между состояниями
под действие оператора
выражается матричным элементом
.
По индексам переход происходитсправа
налево.
Математический смысл
В
гильбертовом пространстве с базисом
и весовой функцией
матричный
элемент оператора
между ортами
и
определяется в виде скалярного
произведения
,
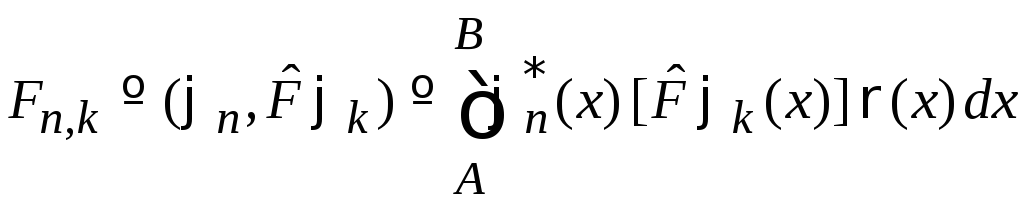(1)
где
A,
B,
–
вещественные.
Физический смысл
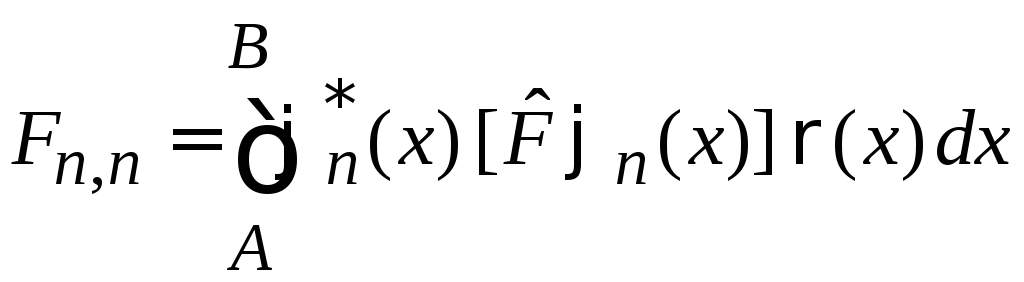
– диагональный
матричный элемент есть среднее значение
величины f,
описываемой оператором 
,
в состоянии 
.
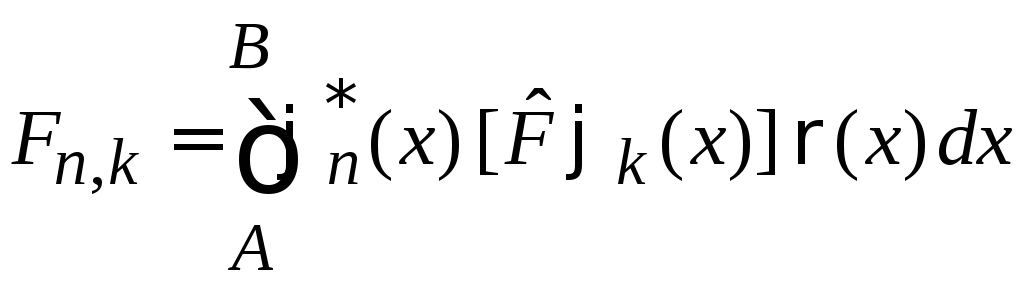
– недиагональный
матричный элемент
есть амплитуда вероятности перехода
между
состояниями
под действием оператора
.
Вероятность
перехода
.
Операторы координаты и импульса
,
.
Эрмитовый оператор
.
(2)
Операция эрмитового сопряжения «+» определяется в виде
,
.
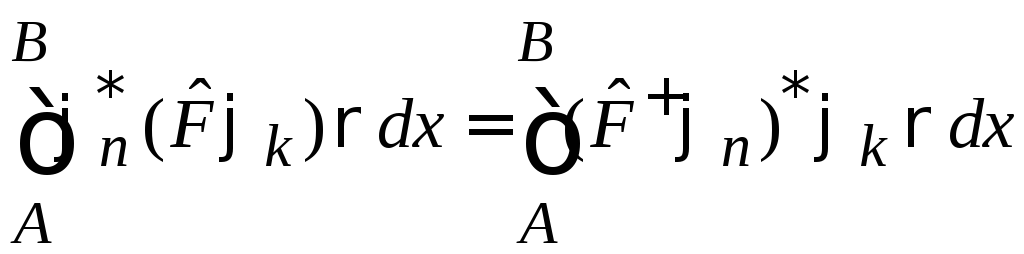Эрмитовый оператор в скалярном произведении функций можно переносить от одного сомножителя к другому
,
.
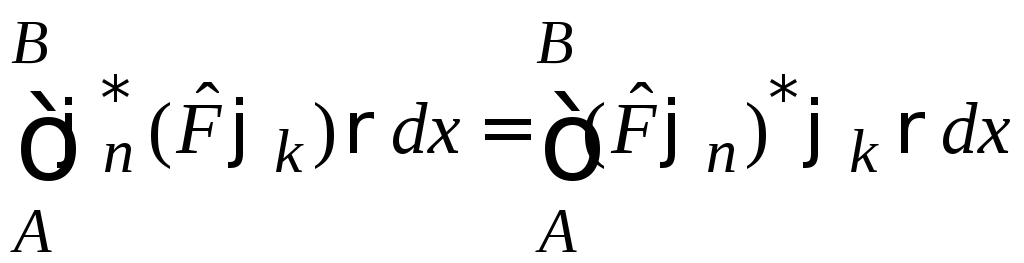(3)
Любой физический оператор является эрмитовым, это обеспечивает вещественность его собственных значений, т. е. результатов измерения соответствующей физической величины.
Соотношения между матричными элементами
Для эрмитового оператора
(4)
– комплексное
сопряжение обращает направление перехода
между состояниями, т. е. течение времени:
.
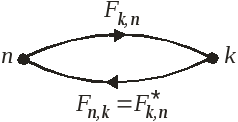
Доказательство:
С учетом
,
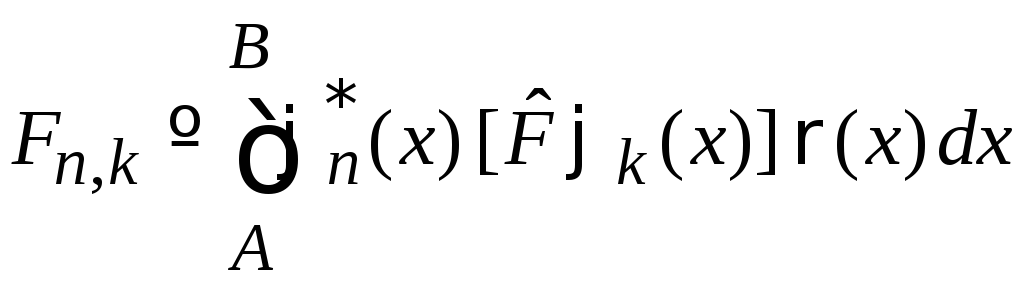(1)
получаем
.
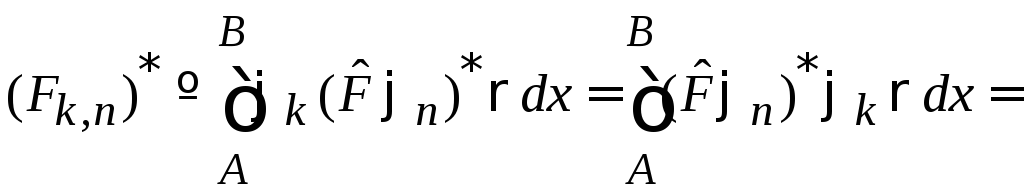
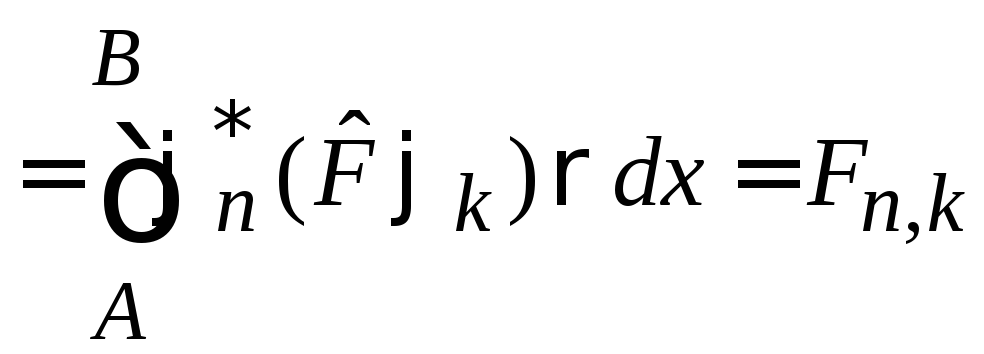Третье равенство следует из эрмитовости (3) оператора.
Матричный элемент произведения эрмитовых операторов
(5)
– переход
под действия
операторов
и
происходит через все возможные
промежуточные состояния
k.
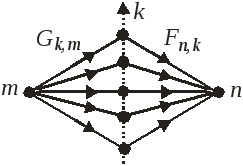
Доказательство:
Из
определения матричного элемента (1) и
эрмитовости
.
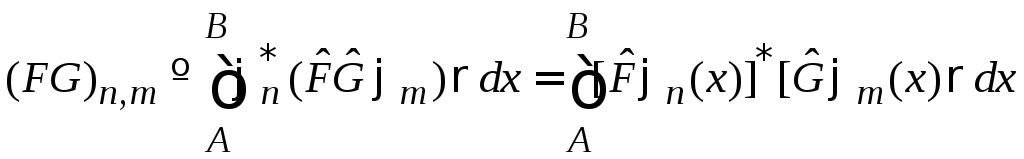Используем фильтрующее свойство δ-функции
,
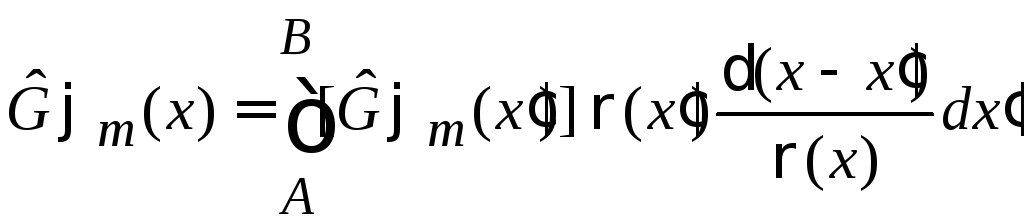тогда
.
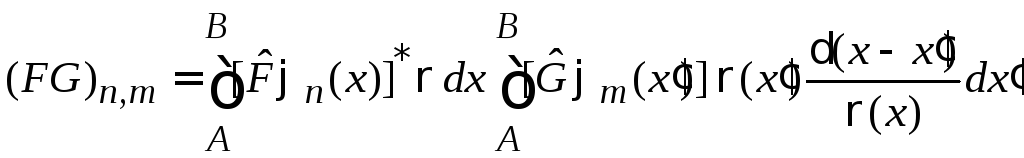Условие полноты базиса
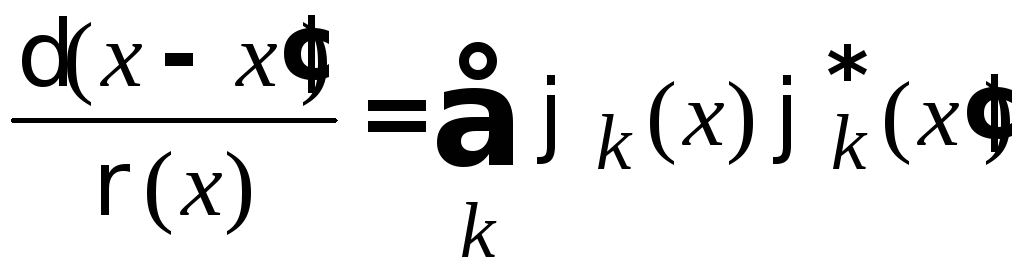
после замены порядка суммирования и интегрирований дает
.
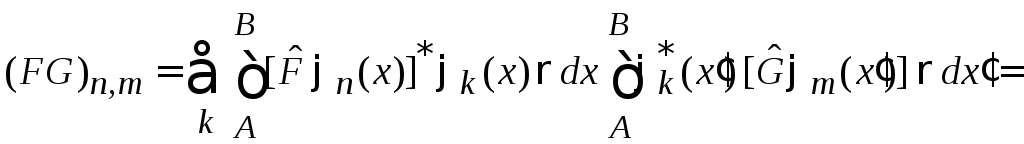
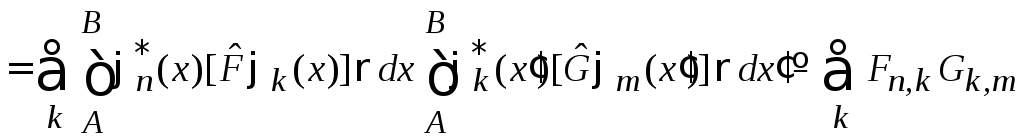