МЕТОДЫ МАТЕМАТИЧЕСКОЙ ФИЗИКИ

Краснопевцев Евгений Александрович

Основная тема курса

Ортонормированные базисы функций

Практическая значимость курса – разложение функций по ортонормированному базису упрощает решение физических и технических задач, результаты получают наглядный физический смысл.

Разделы курса

Преобразование Фурье.

Сингулярные функции:

дельта-функция,

гребенчатая функция,

функция Хевисайда,

функция знака,

прямоугольная функция,

функция sinc,

треугольная функция.

Гамма- и бета-функции Эйлера.

Дифференциальные уравнения второго порядка.

Классические ортогональные полиномы:

Эрмита,

Лагерра,

Лежандра,

Чебышева.

Сферические функции.

Функции Бесселя.

Функция Грина.

Дифференциальные уравнения с частными производными.

КОНТРОЛЬНЫЕ МЕРОПРИЯТИЯ

1. Индивидуальные задания 1, 2, 3.

2. Коллоквиум.

3. Экзамен для группы РН, зачет для групп РМ, РМС, РП, РЭ.

Литература

Краснопевцев Е.А. Математические методы физики. 53

Ортонормированные базисы функций. Изд. НГТУ, 2008. К 782

Дополнительная литература

Бронштейн И.Н., Семендяев К.А.

Справочник по математике для инженеров и учащихся ВУЗов.

ОРТОНОРМИРОВАННЫЕ БАЗИСЫ

Ортогональные координаты упрощают решение задачи, результаты выражаются через скалярные проекции и получают наглядный смысл. Метод применяется во всех разделах физики и техники.

Декартовы ортогональные координаты ввел Рене Декарт (1596–1891) в 1637 г.

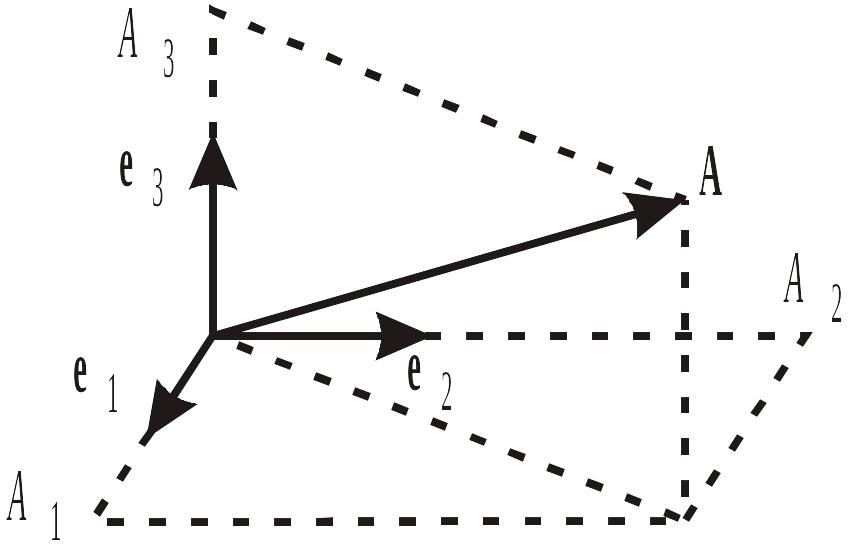
ВекторнЫе пространствА

Векторное пространство – множество векторов, для которых определено скалярное произведение.

3-мерное пространство

Базис ортов

Произвольный трехмерный вектор разлагается по трем ортогональным единичным векторам – ортам, образующим базис:

, .

Операция разложения использует скалярное произведение.

Скалярное произведение векторов

, , .

Если , то вектора ортогональны .

Норма вектора .

Вектор нормирован, если .

Условие ортонормированности базиса

Вектора базиса взаимно ортогональны и нормированы

. (0.1)

Символ Крόнекера

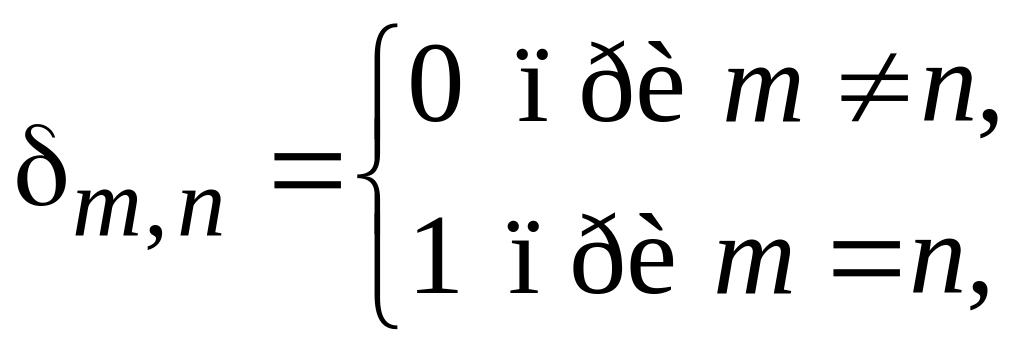(0.2)

ввел Леопольд Крóнекер (1823–1891) в 1866 г.

N-мерное пространство

Базис

, ,

где N – размерность пространства – число независимых векторов, определяющих положение произвольной точки. Базис ортонормирован

.

Разложение вектора на составляющие

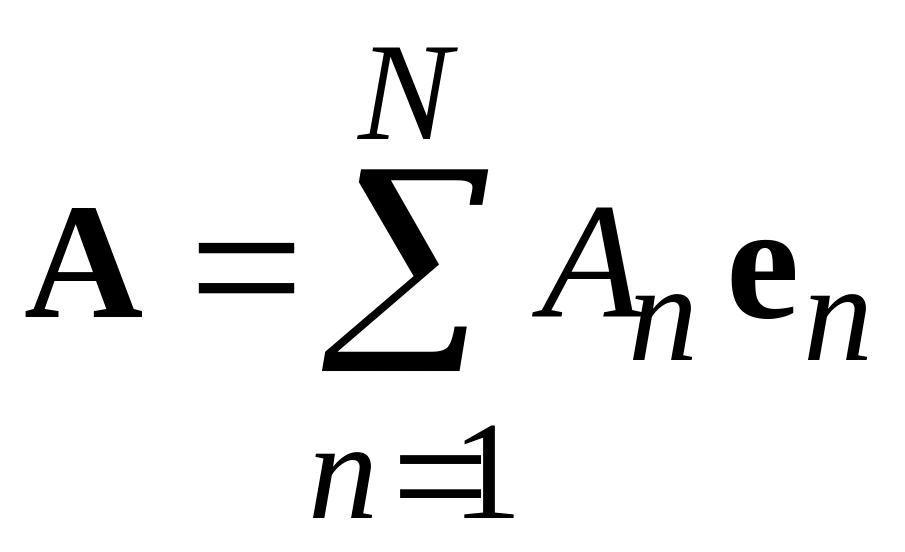. (0.3)

Проекция вектора на орт

. (0.4)

Теорема Пифагора

– квадрат модуля вектора равен сумме квадратов его проекций на ортогональные оси.

От пространства векторов переходим к пространству функций.

Гильбертово пространство с дискретным базисом

Гильбертово пространство – множество комплексных, квадратично интегрируемых функций, для которых определено скалярное произведение.

Базис ортов

, ,

N – размерность пространства – конечное или бесконечное число;

–комплексная, квадратично интегрируемая функция, .

Скалярное произведение

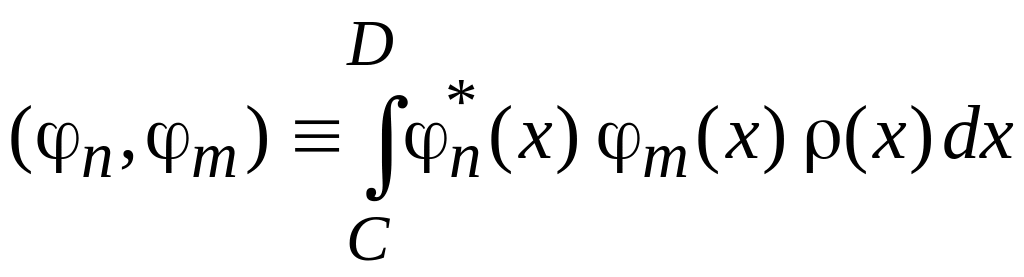, (0.5)

где – вещественная весовая функция; – комплексно сопряженная функция.

Комплексное сопряжение

, , ,

, ,

,

– формула Эйлера, .

Условие ортонормированности базиса

. (0.6)

Разложение функции по базису

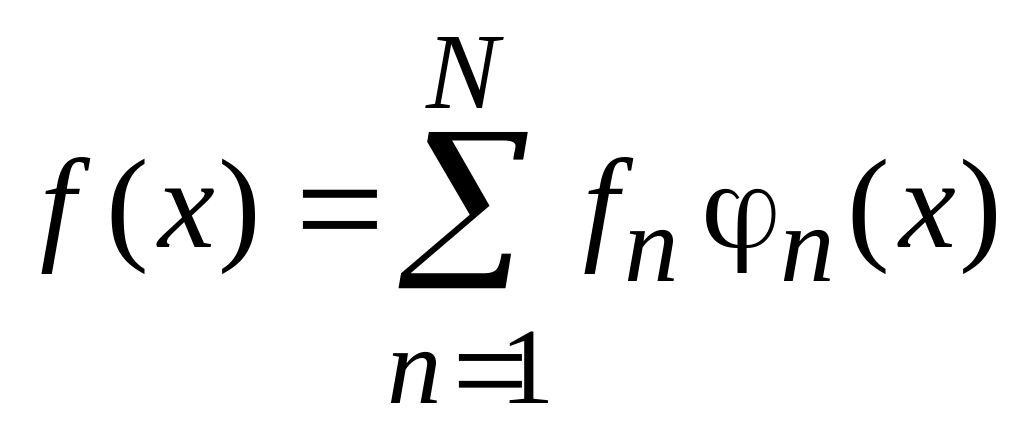, (0.7)

где – множество проекций, или спектр функции f(x):

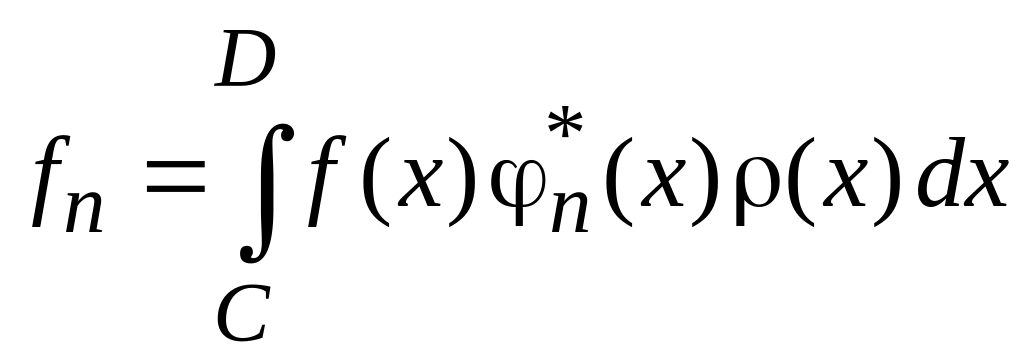. (0.8)

Подстановка (0.8)→(0.7) дает тождество

,

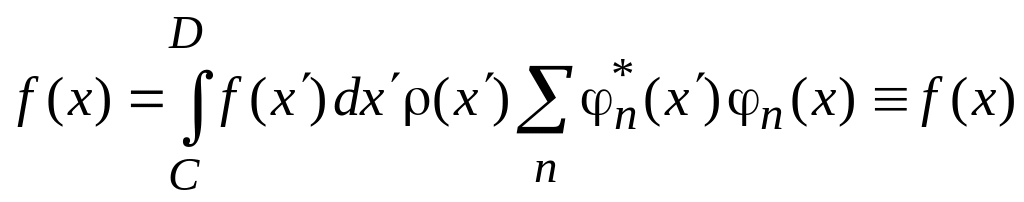если базис полон.

Условие полноты базиса

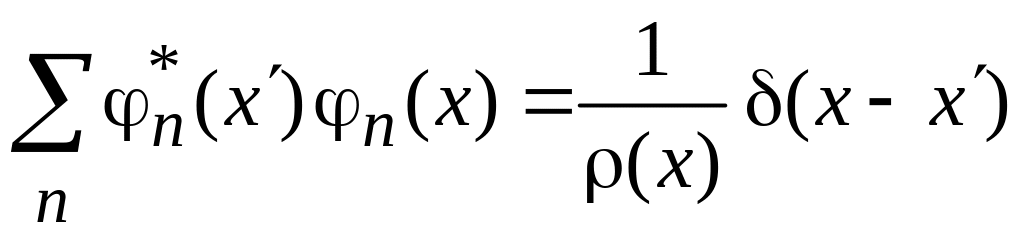, (0.9)

где – дельта-функция,

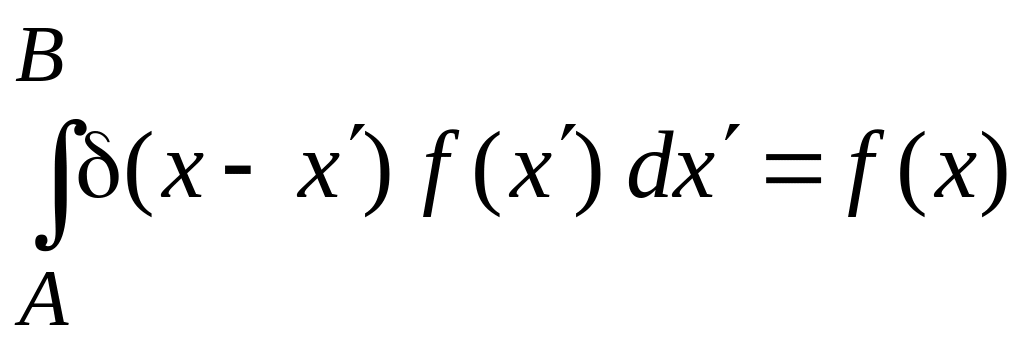– фильтрующее свойство.

Теорема Парсеваля – аналог теоремы Пифагора в пространстве функций

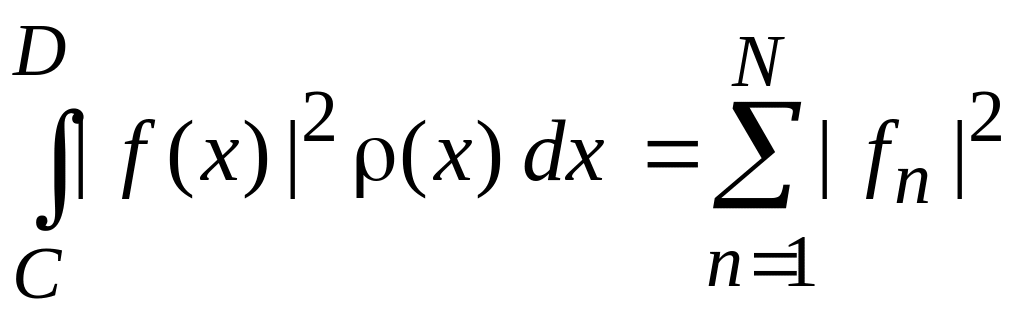, (0.10)

где , . Теорема доказывается подстановкой (0.7) и использованием (0.9).

Гильбертово пространство с непрерывным базисом

Базис ортов , где ; k – непрерывно, . Размерность пространства бесконечная.

Условие ортонормированности базиса

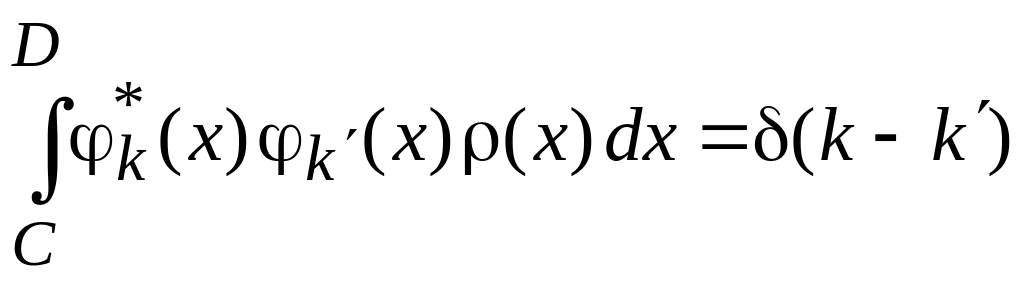, (0.11)

где – дельта-функция.

Разложение функции по базису

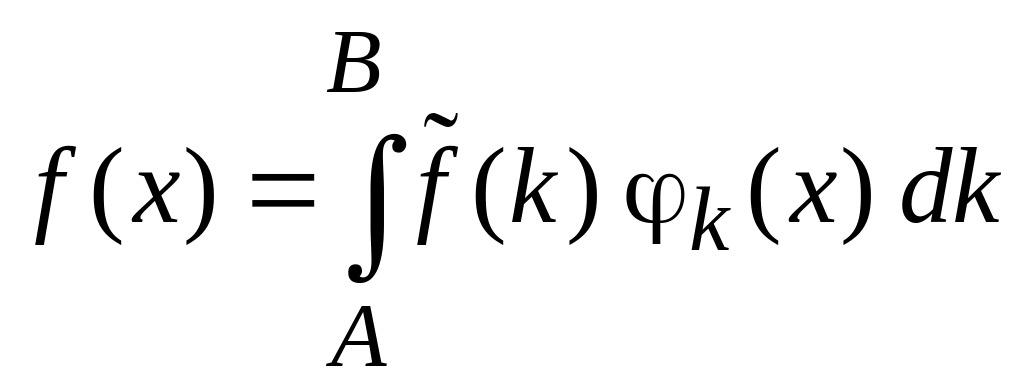. (0.12)

Спектр непрерывный

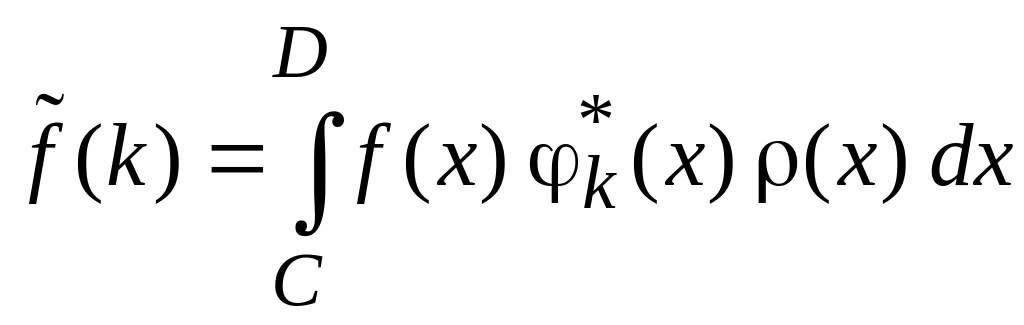. (0.13)

Совпадение спектров функций означает равенство функций.

Подстановка (0.12) в (0.13) дает тождество с учетом (0.11) и фильтрующего свойства дельта-функции.

Условие полноты базиса

. (0.14)

Подстановка (0.13) → (0.12) с учетом (0.14) дает тождество.

Теорема Парсеваля

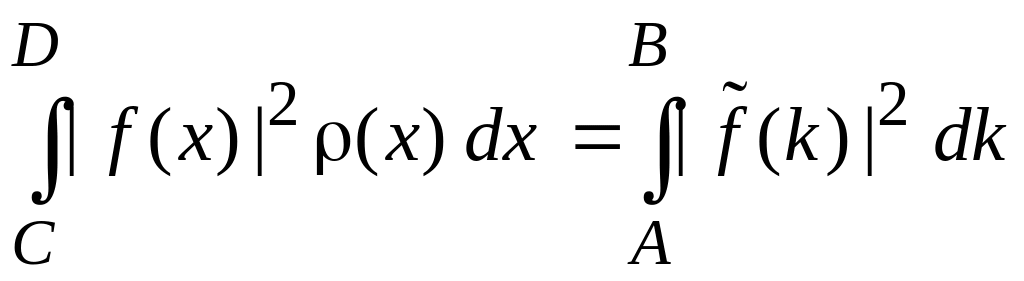(0.15)

доказывается с помощью (0.11) и (0.12), или с помощью (0.13) и (0.14).

Преобразование фурье

Аполлоний Пергский – (ок. 262 – ок. 190 до н.э.) представил сложное движение планеты в виде суммы равномерных вращений по окружностям – эпициклам;

Жан Батист Жозеф Фурье (1768–1830) разложил функцию по гармоническим составляющим в 1807 г.

Бесконечномерный базис гармонических функций

, ; .

Орт является решением волнового уравнения Гельмгольца

,

– плоская волна вдоль оси x.

Выполняются:

условие ортонормированности

,

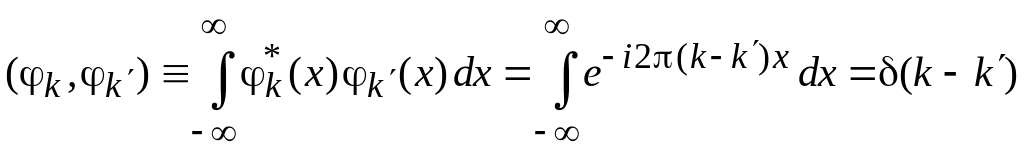условие полноты

.

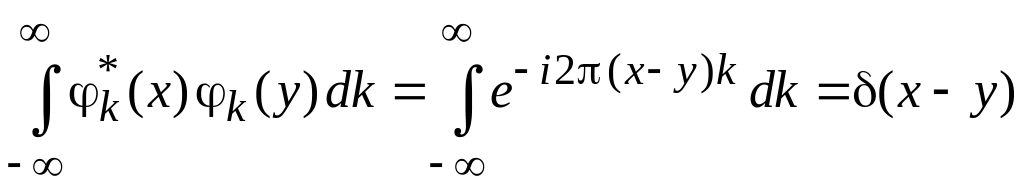Преобразование Фурье – разложение функции по базису

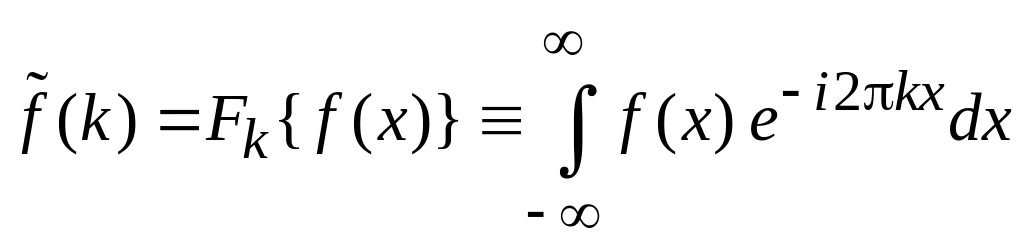, (1.1)

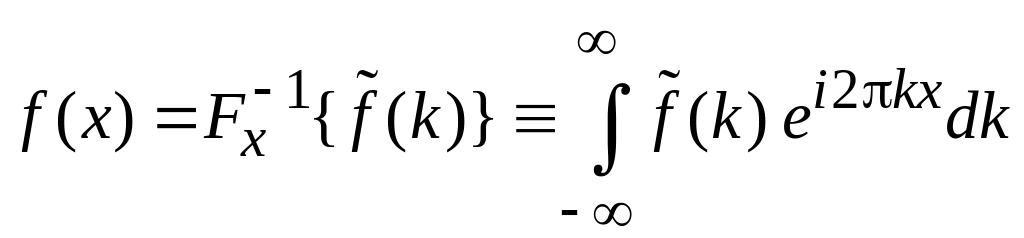, (1.2)

– оператор Фурье, действующий на функцию, находящуюся в , и дающий функцию, зависящую от k;

– оператор обратного преобразования Фурье, дающий функцию, зависящую от x;

– Фурье-образ или спектр функции ;

k и x – Фурье-сопряженные переменные, – безразмерная;

– ядро преобразования, не зависящее от преобразуемой функции.