Вопрос №1(Понятие множества, Конечные и бесконечные множества, Операции над мн-ми)

Понятие множества принадлежит к числу фундаментальных неопределяемых понятий математики. Можно сказать, что множество - это любая определенная совокупность объектов. Объекты, из которых составлено множество, называются его элементами. Элементы множества различны и отличимы друг от друга.

Пример

Множество S страниц в данной книге. Множество N натуральных чисел 1,2,3,... Множество P простых чисел 2,3,5,7,11,... Множество Z целых чисел: ...,-2,-1,0,1,2,... Множество R вещественных чисел. Множества А различных символов на этой странице.

Если объект х является элементом множества М, то говорят, что х принадлежит М.В противном случае говорят, что х не принадлежит М.

Множество не содержащее элементов называется пустым. обычно в конкретных рассуждениях элементы всех множеств берутся из некоторого одного достаточно широкого множества U, которое называется универсумом.

Задание множеств.

Чтобы задать множество нужно указать, какие элементы ему принадлежат. Это можно сделать различными способами:

перечислением элементов: М:={a₁,a₂,...,a_k}

характеристическим предикатом: M:={x|P(x)}

порождающей процедурой: M:={x|x:=f}.

Перечислением можно задавать только конечные множества. Бесконечные множества задаются только характеристическим предикатом или порождающей процедурой. Множества разделяются на непересекающиеся подмножества, которые в сумме содержат все элементы множества.

Бесконечность может быть актуальной и потенциальной.

Потенциальное бесконечное множество - в любой точке конечное множество, однако, для любого n можно найти n+1(например, файл).

Элементы множества различимы. Элементами множества могут быть множества {x,y,...,z}

Операции над множествами.

Объединение, пересечение, разность, симметрическая разность, дополнение(¬).

На булеане P(U) определим операции над множествами A . P(U) и B . P(U). Объединением множеств A и B называется множество C, состоящее из всех тех элементов, которые принадлежат, по крайней мере, одному из множеств A, B. Обозначение: C=A.B. Символическая запись: A.B={x|x.A или x.B}. Пересечением множеств A и B называется множество C, состоящее из всех тех элементов, которые принадлежат каждому из множеств A, B. Обозначение: C=A.B. Символическая запись: A.B={x|x.A и x.B}. Разностью множеств A и B называется множество C, состоящее из всех тех элементов множества A, которые не принадлежат множеству B. Обозначение: C=A\B. Символическая запись: A\B={x|x.A и x.B}. Симметрической разностью множеств A и B называется множество C, состоящее из всех тех элементов, которые принадлежат только одному из множеств A, B. Обозначение: C= A.B. Символическая запись: A.B={x|x.A и x.B или x.A и x.B}=(A\B).(B\A). Дополнением к множеству A называется множество, состоящее из всех тех элементов множества U, которые не принадлежат множеству A. Обозначение: A Символическая запись: A=U\A.

Вопрос №2(Алгебра множеств)

Алгебра множеств включает в себя алфавит, законы и операции.

Алфавит: будем обозначать множества прописными латинскими буквами А,В,…, а элементы принадлежащие данным множествам, - строчными а,в,…

Законы:

1.Коммутативность операций  и :

АВ=ВА АВ=ВА

2.Ассоциативность операций  и :

А(ВС)=(АВ)С А(ВС)=(АВ)С

3.Законы идемпотентности операций  и :

АА=А АА=А

4.Законы дистрибутивности:

А(ВС)=(АВ)(АС) А(ВС)=(АВ)(АС)

5.Законы поглощения:

А(АВ)=А А(АВ)=А

6.Законы де Моргана:

¬(АВ)=¬А¬В ¬(АВ)=¬А¬В

7.Законы пустого и универсального множеств:

АØ=А АØ=Ø А¬А=Ø АU=U AU=A A¬A=U ¬U=Ø ¬Ø=U

8.Законы двойного отрицания:

¬¬А=А

Вопрос №3(Понятие отношения)

Декартовым или прямым произведением множеств A1, A2,..., An называется множество {(x₁, x₂,..., x_n| xєA₁, xєA₂, ..., xєA_n)} обозначаемое через A₁xA₂x...xA_n.

N-местным отношением P или n-местным предикатом P на множествах A₁, A₂,...,A_n называется любое подмножество прямого произведения A₁xA₂x...xA_n.Элементы x₁, x₂, ..., x_n называются связанными соотношением P тогда и только тогда, когда (x₁,x₂,…,x_n)принадлежит P.

При n=1 отношением P является подмножеством множества А₁ и называется унарным отношением, или свойством, на множестве А₁.

При n=2 отношением Р называется бинарным отношением.

Отношение РАⁿ называется n-местным отношением(предикатом) на множестве А.

Бинарное отношение.

Пусть Р – некоторое бинарное отношение.

Областью определения Р называется множество _Р={x|(x,y)єP для некоторого у}

Областью значения Р называется _Р={y|(x,y,)єP для некоторого х}

Обратным к Р отношением называется множество Р^-1={(y,x)|(x,y)єP}

Образом множества Х относительно Р называется множество P(X)={y|(x,y)єP для некоторого xєX}

Множество Р^-1(Х) называется прообразом множества Х относительно Р.

Произведением бинарных отношений P₁AxB и P₂ВxС называется множество P₃=Р₁Р₂ ,где P₃=АхС и P₃={(x,y)|xєA yєC и найдётся zєB такой, что (x,z)єP₁ и (z,y)єP₂}

Ориентированный граф – рисунок отношения.

Вопрос №4(Отношение эквивалентности, Основная теорема, Фактор-множество)

Отношение эквивалентности – отношение(рефл., транз., симметр.)

1. Рефлексивность <x,x>є

2. Симметричность <x,y>є –><y,x>є

3. Транзитивность <x,y>є, <y,z>є–><x,z>є

Пример: равенство.

Отношение эквивалентности реализует разбиение  на непересекающиеся подмножества, в сумме дающие . В отношении эквивалентности множества всех пар разбивается на не пересекающиеся классы эквивалентности. В класс эквивалентности попадают пары обладающие одним свойством. Отношение эквив. позволяет собрать пары с одним похожим свойством. Два класса эквив-ти либо не пересекаются, либо совпадают. Каждый элемент множества Х принадлежит классу эквивалентности.

Теорема:

Пусть  - есть отношение эквивалентности на Х, тогда система  классов эквивалентности представляет собой разбиение множества Х

Обратно. Если Ф(х) – некоторое разбиение множества Х, а отношение  определяется так, что элемент <а,в>є, если существует Ає(х):<а,в>єА, тогда отношение не эквивалентности. Каждое отношение эквивалентности задает разбиение множества Х.

Фактор-множество – множество классов эквивалентности множества Х. Все множества разбиения определённого множества Х.

Тождественное отношение задаёт самое подробное разбиение на классы эквивалентности.

Z⁺xZ⁺ <x,y>~<u,v> x/y=u/v

Пример: <2,3>~<4,6>є отношению Кильда. В класс экв. Попадают все числа вида 2/3,4/6,…

В класс экв. всегда «складываем» элементы, которые по некоторым свойствам неразличимы. (например, но множестве людей отношение – быть рыжим)

Вопрос №5(Обобщенное равенство, Абстракция)

Вопрос №6(Понятие функции, График Функции, Суперпозиция функций)

Функцией называется функциональное соответствие. Если f устанавливает соответствие между множествами А и В, то говорят, что функция имеет тип А–>В(обозначается f:A–>B). Каждому элементу а из области определение функции f ставит в соответствие элемент в из области значения. Это обозначается f(a)=b. Элемент а – аргумент функции, элемент b – значение функции на а.

Отображением А в В называется всюду определённое и при этом сюрьективное функциональное соответствие f:A–>B

Отображение типа А–>А часто называют преобразованием множества А. Функция типа А–>А, являющееся отображением множества А на А, называется перестановкой на А.

Функции f и g равны, если:

1. их области определения – одно и тоже множества А

2. для любого аєА f(a)=g(a).

Функция типа f:A₁xA₂x…xA_n–>B называется n-местной.

Пусть дано соответствие GАхВ. Тогда соответствие НВхА называется обратным к G(G^-1), если Н таково, что (b,a)єН тогда и только тогда, когда (a,b)єG.

Если соответствие, обратное к функции f:A–>B, является функциональным, то оно называется функцией, обратной к f (f^-1). Для функции f:A–>B обратная ф-я существует тогда и только тогда, когда f является взаимно однозначным соответствием между своими областями определения и значений.

Пусть даны ф-ии f: A–>B и g: B–>C. Функция h: A–>C называется композицией функций f и g (f◦g), если имеет место равенство h(x)=g(f(x)), где хєА.

Часто говорят, что функция h получена подстановкой f в g. Для многоместных функций f:A^m–>B, g:Bⁿ–>C возможны различные варианты подстановки f и g, дающие ф-ии различных типов. Например, при m=3 и n=4 функция h=g(x₁,f(y₁,y₂,y₃),x₃,x₄) имеет шесть аргументов и тип ВхА³хВ²–>С.

Ф-я, полученная из f₁,…,f_n некоторой подстановкой их друг в друга и переименованием аргументом, называется суперпозицией f₁,…,f_n. Выражение, описывающее эту суперпозицию и содержащее функциональные знаки и символы аргументов называются формулой.

Функция f называется инъекцией, если для всех x1, x2 из того, что x1.x2, следует f(x1).f(x2).

Функция f называется сюръекцией, если .f =B. Функция f называется биекцией (взаимно однозначным соответствием между множествами A и B), если она инъективна и сюръективна.

Вопрос №7(Отношение порядка,Частичный порядок, Изоморфизм ЧУМ)

Отношение порядка. Если отказаться от свойства симметрии <x, y> , а <y, x>.

Отношением частичного порядка будем называть рефл., транз., антисим. отношение. ’=(УхУ). Частично упорядоченное множество У, являющееся подмножеством мн-ва Х, если отн-ние (УхУ) является отношением частичного порядка.

Отношение предупорядочения – рефл. и транз. отношение. Предупорядочение позволяет «завести» выражение частичного порядка. Отношение предупорядочения позволяет разбить множество Х на классы эквивалентности элементов и на множестве таких классов определить отношение частичного порядка.

Линейное упорядочкение. Отношение  - есть лин. упор., если оно является <x,y>є либо <х,у>є.

На множестве всех подмножеств мн-ва Х можно выявить отношение включения(не является отношением линейного порядка).

Частичноупор. мн-во называется вполнеупорядоченным, если каждое его не пустое подмножество имеет наименьший элемент.

Вопрос №8(Аксиоматические теории, Непротиворечивость и полнота системы аксиом)

Чтобы задать формальную аксиоматическую теорию, необходимо определить:

1. некоторое счетное множество символов (алфавит) – символов теории Т(конечные последовательности символов в теории Т называются выражениями теории Т);

2. Подмножество выражений теории Т, называемых формулами;

3. Подмножество формул теории Т, называемых аксиомами.

4. Конечное множество R₁, R₂, …, R_m отношений между формулами, называемых правилами вывода.

Если А и формулы А₁,А₂,…,А_i находятся в некотором отношении R_k,то А называется непосредственным следствием из формул А₁,А₂,…,A_i, полученным по правилу R_k.

Выводом в теории Т называется всякая последовательность ₁, ₂,…, _n формул такая, что для любого i формула _i есть либо аксиома теории Т, либо непосредственное следствие каких-либо предыдущих формул.

Формула А называется теоремой теории Т, если в ней существует вывод, в котором последней формулой является А.

Формула А называется следствием множества формул Г тогда и только тогда, когда существует такая последовательность формул ₁, ₂,…, _n, что _n есть А, и для любогоi, 1<=i<=n, _I есть либо аксиома, либо формула из Г, либо непосредственное следствие некоторых предыдущих формул. Эта последовательность называется выводом из А в Г. элементы называются посылками вывода или гипотезами. Сокращено можно записать Г├А. Если множество Г состоит из формул В₁,В₂,…,В_k, то пишут В₁,В₂,…,В_k├А, и говорят, что формула А выводима из формул В₁,В₂,…,В_k. Если Г – пустое множество, то Г├А тогда и только тогда, когда А есть теорема. В этом случае принято писать ├А и говорить, что формула А доказуема, а сам вывод (последовательность формул) называют доказательством.

Формальная аксиоматическая теория называется полной, если в ней доказуема любая тавтология.

Формальная аксиоматическая теория называется непротиворечивой, если в ней не существует вывода формулы А такой, что одновременно доказуемы формулы А и ¬А.

Формальную аксиоматическую теорию называют полной в узком смылсе, если добавление любой невыводимой формулы в качестве схемы и аксиом приводит к противоречивой системе.

Одним из важных примеров аксиоматической теорией может служить ИВ (один из возможных способов формализации логики высказывании).

Вопрос №9(Система аксиом ив, Полнота и независимость системы аксиом)

1. Алфавит ИВ образуют буквы А,В,С,… и т.д. (возможно с индексами), которые называются пропозициональными переменными, логические символы (связки), ¬, , , , а также вспомогательные символы скобок (,).

2. Множество формул ИВ определяется индуктивно:

а) все пропозициональные переменные являются формулами ИВ;

б) если А и В формулы ИВ, то (¬А), (АВ), (АВ), (АВ) – формулы ИВ;

в) выражение является формулой ИВ тогда и только тогда, когда это может быть установлено с помощью пунктов а) и б).

3. Аксиомы ив

Посотри в методичке по дискретке!!!

4. Единственным правилом вывода в ИВ является правило заключения (modus ponens):если А и АВ – выводимые формулы, то В – также выводимая формула. Запись – А,АВ/В.

Выводом А₁,А₂,…,An├А называется последовательность формул ₁, ₂,…, _m, А, в которой любая формула либо является одной из формул А₁,А₂,…,An (т.е. посылкой), либо аксиомой, либо подстановкой в аксиому, либо получается из предыдущих формул по правилу вывода.

ИВ – непротиворечивая, полная аксиоматическая теория, причём ИВ полно и в узком смысле.

Вопрос №10(Интерпретация ИВ, Распределение Истинностных значений формулы)

Под высказыванием принято понимать языковое предложение, о котором имеет смысл говорить, что оно истинно или ложно. В логике высказываний интересуются не содержанием, а истинностью или ложностью высказываний. Истинностное значение – истина или ложь – будем обозначать И и Л соответственно.

Логические операции (связки) Отрицанием высказывания P называется высказывание, истинное тогда и

только тогда, когда высказывание P ложно. Обозначается ¬P. Конъюнкцией двух высказываний P и Q называется высказывание, истинное тогда и только тогда, когда истинны оба высказывания. Обозначается P.Q.

Дизъюнкцией двух высказываний P и Q называется высказывание, ложное тогда и только тогда, когда оба высказывания ложны. Обозначается P.Q. Импликацией двух высказываний P и Q называется высказывание, ложное тогда и только тогда, когда P истинно, а Q ложно. Обозначается P.Q. Эквиваленцией двух высказываний P и Q называется высказывание, истинное тогда и только тогда, когда истинностные значения P и Q совпадают. Обозначается P.Q. Алфавит логики высказываний содержит следующие символы: высказыва-

тельные переменные – обычно заглавные латинские буквы; логические символы ¬, ., ., ., .; символы скобок (, ).Последовательность символов в логике высказываний называется формулой, если она удовлетворяет следующему определению:

1) любая высказывательная переменная – формула;

2) если A и B – формулы, то ¬A, A.B, A.B, A.B, A.B, (A) – формулы.

Если каждой высказывательной переменной, входящей в формулу, придавать истинностное значение И и Л, то формула будет определять истинностную функцию, т.е. функцию, определенную на множестве { } С,о

n (n – число высказывательных переменных) со значениями в множестве {И, Л}. Если, кроме того, принять И=1, Л=0, то любую формулу логики высказываний можно интерпретировать как формулу логики переключательных функций. По аналогии с переключательными функциями, для любого высказывания можно построить таблицу истинности. Упорядоченный набор высказывательных переменных <X1, X2, ..., Xk> на-

зовем списком переменных формулы A, если все переменные формулы A содержатся в этом наборе. В списке переменных формулы A часть переменных может быть фиктивной, т.е. может не входить явно в формулу A. Очевидно, что если список переменных для формулы A содержит k переменных, то таблица

истинности для формулы A будет содержать 2k строк. Пусть A и B – две формулы, зависящие от одного и того же списка переменных <X1, X2, ..., Xk>. Будем называть их равносильными (обозначается A=B),

если на любом наборе значений переменных они принимают одинаковые значения. Отношение равносильности есть отношение эквивалентности. В логике высказываний действуют выведенные нами ранее равносильности для переключательных функций. Тождественно-истинные формулы. Правильные рассуждения

Пусть формула A зависит от списка переменных <X1, X2, ..., Xk>. Формула A называется тавтологией (тождественно-истинной формулой – ТИФ), если при любых значения переменных списка <X1, X2, ..., Xk> она принимает значение И. Формула A называется выполнимой (условно-истинной формулой – УИФ),

если при некоторой значениях переменных списка <X1, X2, ..., Xk> она принимает значение И. Формула A называется тождественно-ложной формулой – ТЛФ, если при любых значениях переменных списка <X1, X2, ..., Xk> она принимает значение Л. Формула A называется опровержимой (условно-ложной формулой), если при некоторых значениях переменных списка <X1, X2, ..., Xk> она принимает значение Л. При доказательстве утверждений в математических теориях обычно используют рассуждения. На языке логики эти рассуждения можно выразить формулами. Рассуждения называются правильными, если они построены по законам

формальной логики и из конъюнкции посылок следует заключение, т.е. всякий раз, когда все посылки истинны, заключение тоже истинно. Пусть P1, P2, ..., Pn – посылки, D – заключение. Тогда для определения правильности рассуждения по схеме 1 2 , , ,n P P P D … , т.е. утверждения о том, что из данных посылок P1, P2, ..., Pn следует заключение D, требуется установить тождественную истинность формулы (P1.P2.....Pn).D.

Так как речь идет лишь о правильности рассуждения, истинность заключения не является ни необходимым, ни достаточным условием правильности рассуждения. Наиболее распространенными схемами правильных рассуждений являются следующие схемы: Рассмотрим условное высказывание A.B, где A – конъюнкция посылок, B – заключение. Иногда удобнее вместо доказательства истинности этого условного высказывания установить логическую истинность некоторого другого высказывания, равносильного исходному. Такие формы доказательства называются косвенными методами доказательства. Одним из них является способ доказательства от противного. Предположим, что утверждение A.B ложно. Тогда, исходя их этого предположения, приходим к противоречию и доказываем, что некоторое утверждение (соответствующее высказыванию C) выполняется и не выполняется (одновременно). Применимость этой формы косвенного метода доказательства оправдывается равносильностью A.B=¬(A.B).(C.¬C)=(A.¬B).(C.¬C). Существуют и другие схемы доказательства от противного: A.B=(A.¬B).¬A, A.B=(A.¬B).B. Ещё одной формой косвенного метода доказательства является доказательство по закону контрапозиции, основанное на равносильности

A.B=¬B.¬A, когда вместо истинности A.B доказывается истинность ¬B.¬A.

Вопрос №11(Вывод в ИВ)

Чтобы задать формальную аксиоматическую теорию, необходимо определить: 1) некоторое счётное множество символов (алфавит) – символов теории Т (конечные последовательности символов теории Т называются выражениями теории Т); 2) подмножество выражений теории Т, называемых формулами; 3) подмножество формул теории Т, называемых аксиомами; 4) конечное множество R1, R2, ..., Rm отношений между формулами, называемых правилами вывода. Если A и формулы A1, A2, ..., Ai находятся в некотором отношении Rk, то A называется непосредственным следствием из формул A1, A2, ..., Ai, полученным по правилу Rk.

Выводом в теории Т называется всякая последовательность .1, .2, ..., .n формул такая, что для любого i формула .i есть либо аксиома теории Т, либо непосредственное следствие каких-либо предыдущих формул.

Формула A называется теоремой теории Т, если в ней существует вывод, в котором последней формулой является A. Формула A называется следствием множества формул Г тогда и только тогда, когда существует такая последовательность формул .1, .2, ..., .n, что .n есть A, и для любого i, 1.i.n, .i есть либо аксиома, либо формула из Г, либо непосредственное следствие некоторых предыдущих формул. Эта последовательность называется выводом A из Г. Элементы Г называются посылками вывода или гипотезами. Сокращенно можно записать Г..A. Если множество Г состоит их формул B1, B2, ..., Bk, то пишут B1, B2, ..., Bk..A, и говорят, что формула A выводима из формул B1, B2, ..., Bk. Если Г – пустое множество, то Г..A тогда и только тогда, когда A есть теорема. В этом случае принято писать ..A и говорить, что формула A доказуема, а сам вывод (последовательность формул) называют доказательством. Формальная аксиоматическая теория называется полной, если в ней доказуема любая тавтология. Формальная аксиоматическая теория называется непротиворечивой, если в ней не существует вывода формулы A такой, что одновременно доказуемы формулы A и ¬A. Формальную аксиоматическую теорию называют полной в узком смысле, если добавление любой невыводимой формулы в качестве схемы аксиом приводит к противоречивой системе. Одним из важных примеров аксиоматической теории может служить исчисление высказываний (один из возможных способов формализации логики высказываний). Определим эту формальную аксиоматическую теорию следующим образом:

1. Алфавит ИВ образуют буквы A, B, C... и т.д. (возможно с индексами), которые называются пропозициональными переменными, логические символы (связки) ¬, ., ., ., а также вспомогательные символы скобок (, ).

2. Множество формул ИВ определяется индуктивно:

а) все пропозициональные переменные являются формулами ИВ;

б) если A и B формулы ИВ, то (¬A), (A.B), (A.B), (A.B) – формулы ИВ;

в) выражение является формулой ИВ тогда и только тогда, когда это может быть установлено с помощью пунктов а) и б). Договоримся далее опускать внешние скобки у формулы

3. Аксиомы ИВ (система Клини).

1) A.(B.A)

2) (A.B).((A.(B.C)).(A.C))

3) A.(B.A.B)

4) A.B.A 5) A.B.B

6) A.A.B 7) B.A.B

8) (A.C).((B.C).(A.B.C))

9) (A.B).((A.¬B).¬A)

10) 洵A.A

4. Единственным правилом вывода в ИВ является привило заключения (modus ponens): если A и A.B – выводимые формулы, то B – также выводимая формула. Символическая запись:

.

Выводом A1, A2,..., An.. A называется последовательность формул .1, .2,..., .m, A, в которой любая формула либо является одной из формул A1, A2,..., An (т.е. посылкой), либо аксиомой, либо подстановкой в аксиому, либо получается из предыдущих формул по правилу вывода. Исчисление высказываний - непротиворечивая, полная аксиоматическая теория, причем ИВ полно и в узком смысле.

Вопрос №12(Кванторы, Интерпретация ИП)

Квантором называется функция Р(х_1,х₂,…,х_n) переменные которой принимают значения из некоторого множества М, а сама она принимает два значения: И(истинное) и Л(ложное),т.е. Р(х_1,х₂,…,х_n):Мⁿ –>{И,Л}.

Предикат от n аргументов называют n-местным предикатом. Множество М значений переменных определяется обычно математическим контекстом.

Предикаты обозначаются прописными буквами латинского алфавита. Иногда бывают удобно указывать число переменных у предикатов. В таких случаях у символов предикатов пишут верхний индекс, который и указывает число аргументов, например: P⁽ⁿ⁾(x₁,x₂,…,x_n) – n-местным предикат. Высказывания считаются нуль-местными предикатами.

Над предикатами можно производить обычные логические операции. В результате этих операций получаются новые предикаты.

Кроме операций логики высказываний, для построения новых предикатов используются операции связывания квантором.

Квантор всеобщности. Пусть Р(х) – некоторой предикат, принимающий значение И или Л для каждого элемента множества М. Тогда под выражением хР(х) будем подразумевать высказывание истинное, когда Р(х) истинно для каждого элемента х из множества М, и ложное – в противном случае. Это высказывание уже не зависит от х. Символ х называется квантором всеобщности.

хР(х)(по df)Р(х₁) Р(х₂)…

Квантором существования. Пусть Р(х) – некоторый предикат. Под выражением хР(х) будем понимать высказывание истинное, когда существует элемент множества М, для которого Р(х) истинно, и ложное – в противном случае. Это высказывание уже не зависит от х. Символ х называется квантором существования.

хР(х) (по df)Р(х₁) Р(х₂)…

Вопрос №13(Система аксиом теории предикатов первого порядка)

Предикатом называется функция P(x1, x2, ..., xn), переменные которой принимают значения из некоторого множества M, а сама она принимает два значения: И (истинное) и Л (ложное), т.е. P(x1,x2,...,xn): { } С,о n M > . Предикат от n аргументов называют n-местным предикатом. Множество M значений переменных определяется обычно математическим контекстом. Предикаты обозначаются прописными буквами латинского алфавита. Иногда бывает удобно указывать число переменных у предикатов. В таких случаях у символов предикатов пишут верхний индекс, который и указывает число аргументов, например: P(n) (x1,x2,...,xn) – n-местный предикат. Высказывания считаются нуль-местными предикатами. Над предикатами можно производить обычные логические операции. В результате этих операций получаются новые предикаты. Кроме операций логики высказываний, для построения новых предикатов используются операции связывания квантором. Квантор всеобщности. Пусть P(x) – некоторый предикат, принимающий значение И или Л для каждого элемента множества M. Тогда под выражением .xP(x) будем подразумевать высказывание истинное, когда P(x) истинно для каждого элемента x из множества M, и ложное – в противном случае. Читается

это выражение так: «для всех x P(x)». Это высказывание уже не зависит от x. Символ .x называется квантором всеобщности. ( ) ( ) ( ) 1 2 xP x P x P x . . . . def

_

Квантор существования. Пусть P(x) – некоторый предикат. Под выражением .xP(x) будем понимать высказывание истинное, когда существует элемент множества M, для которого P(x) истинно, и ложное – в противном случае. Читается это выражение так: «существует x такое, что P(x)». Это высказывание уже не зависит от x. Символ .x называется квантором существования. ( ) ( ) ( ) 1 2 xP x P x P x . . . . def

_

Пример. Пусть P(x)=«x делится на два», Q(x)=«x делится на три». Тогда .x(P(x).Q(x)) – истинное высказывание; .x(P(x).Q(x)) – ложное высказывание. Алфавит логики предикатов содержит следующие символы:

1) символы предметных переменных – обычно строчные латинские буквы с индексами или без них;

2) символы предикатов – обычно прописные латинские буквы с индексами или без них; 3) логические символы: ¬, ., ., ., .; 4) символы кванторов – ., .; 5) скобки и запятую. Слово в алфавите логике предикатов называется формулой, если оно удовлетворяет следующему индуктивному определению:

1) Если P – символ предиката, x1, x2,..., xn – символы предметных переменных, то P(x1,x2,...,xn) – формула. Такая формула называется атомарной. Все предметные переменные атомарных формул свободные, связанных переменных нет.

2) Пусть A – формула. Тогда ¬A тоже формула. Свободные и связанные переменные формулы ¬A – это соответственно свободные и связанные переменные формулы A.

3) Пусть A и B – формулы, причем нет таких предметных переменных, которые были бы связаны в одной формуле и свободны в другой. Тогда A.B, A.B, A.B, A.B есть формулы, в которых свободные переменные формул A и B остаются свободными, а связанные переменные формул A и B остаются

связанными.

4) Пусть A – формула, содержащая свободную переменную x. Тогда .xA, .xA тоже формулы, Переменная x в них связана. Остальные переменные, которые в формуле A свободны, остаются свободными, а переменные, которые в формуле A связаны, остаются связанными. Говорят, что формула A есть область действия квантора.

5) Слово в алфавите логики предикатов 1–5 является формулой только в том случае, если это следует из правил 1–4. Заметим, что по определению формулы никакая переменная не может быть одновременно свободной и связанной. Значение формулы определено лишь тогда, когда задана какая-нибудь интерпретация входящих в нее символов. Под интерпретацией (моделью) понимают систему D=<M, f>, состоящую из непустого множества M и соответствия f, которое для каждого предикатного символа A(n) определяет n-местный предикат.

4.2. РАВНОСИЛЬНОСТЬ ФОРМУЛ

Пусть формулы F и G имеют одно и то же множество свободных переменных. Формулы F и G равносильны в данной модели, если на любом наборе значений свободных переменных они принимают одинаковые значения. Формулы F и G равносильны на множестве M, если они равносильны во всех моделях, заданных на множестве M. Формулы F и G равносильны (в логике предикатов), если они равносильны на всех множествах (тогда будем писать F=G). Пример. На множестве M={a,b} зададим предикаты P1(x,y) и P2(x,y). x y P1

(x,y) P2(x,y)

a a И И

a b Л И

b a Л Л

b b И Л

Рассмотрим две формулы

Q(x1,x2).Q(x1,x3), (1)

Q(x1,x2).Q(x2,x3). (2)

Если областью модели служит множество M и формула Q интерпретируется как предикат P1, то формулы (1) и (2) равносильны в этой модели, так как принимают значение И только на двух наборах свободных переменных <a,a,a> и <b,b,b>. Если областью модели является то же множество M, но формула Q интер-

претируется как предикат P2, то формулы (1) и (2) не равносильны, так как на наборе <a,b,b> формула (1) принимает значение И, а формула (2) – значение Л. Укажем несколько правил перехода от одних формул к другим, им равносильным (во всех моделях). Основные равносильности логики предикатов

1) .x.yP(x,y)=.y.xP(x,y), .x.yP(x,y)=.y.xP(x,y).

2) .x.yP(x,y)..y.xP(x,y), .y.xP(x,y)..x.yP(x,y).

3) 8.xP(x)=.x ¬P(x), 8.xP(x)=.x ¬P(x).

4) .xP(x)..xQ(x)=.x(P(x).Q(x)), но .xP(x)..xQ(x)..x(P(x).Q(x)).

5) .xP(x)..xQ(x)=.x(P(x).Q(x)), но .xP(x)..xQ(x)..x(P(x).Q(x)).

6) Если в формуле C нет свободной переменной x, то

.xP(x).C=.x(P(x).C), .xP(x).C=.x(P(x).C).

Приведенные формулы

Формулы, в которых из логических символов имеются только символы ., ., ¬, причем символ 8 встречается лишь перед символами предикатов, будем называть приведенными формулами. Для любой формулы существует равносильная ей приведенная формула, причём множества свободных и связанных переменных этих формул совпадают. Такая формула называется приведенной формой данной формулы. Приведенная формула называется нормальной, если она не содержит символов кванторов или все символы кванторов стоят в начале формулы (т.е. логические символы и символы предикатов стоят в области действия каждого кван-

тора). Для любой приведенной формулы существует равносильная ей нормальная формула той же длины. Такая формула называется нормальной формой данной приведенной формулы. Выполнимость. Общезначимость. Рассмотрим некоторую модель с множеством M. Говорят, что формула A выполнима в данной модели если существует набор <a1, a2, ..., an>, ai.M, значений свободных переменных x1, x2, ..., xn формулы

A такой, что (( ( 1 2 , , , С n a a a A = …

.

Говорят, что формула A истинна в данной модели, если она принимает значение И на любом наборе <a1, a2, ..., an>, ai.M, значений своих свободных переменных x1, x2, ..., xn. Говорят, что формула A общезначима или тождественно истинна (в логике предикатов), если она истинна в каждой модели. Говорят, что формула A выполнима (в логике предикатов), если существует модель, в которой A выполнима. Формула A общезначима тогда и только тогда, когда формула ¬A не является выполнимой, и формула A выполнима тогда и только тогда, когда формула ¬A не является общезначимой. Теорема Чёрча. Не существует алгоритм, который для любой формулы логики предикатов устанавливает, общезначима она или нет.

Вопрос №14(Вывод в теории предикатов теории первого порядка)

В логике предикатов, в отличие от логики высказываний, нет эффективного способа для распознавания общезначимости формул. Поэтому аксиоматический метод становится существенным при изучении формул, содержащих кванторы. Выделение общезначимых формул, так же как и в исчислении высказываний, осуществляется путем указания некоторой совокупности формул, которые называются аксиомами, и указания правил вывода, позволяющих из одних общезначимых формул получать другие общезначимые формулы.

Исчисление предикатов – это аксиоматическая теория: Алфавит – те же символы, что и в логике предикатов.

Понятие формулы – совпадает с понятием формулы в логике предикатов. Аксиомы:

1) 1 . 10. – аксиомы Клини исчисления высказываний

2) .xA(x).A(y) (.-схема)

3) A(y)..xA(x) (.-схема)

Система правил вывода:

1)

, A A B

B

. modus ponens (m.p.)

2) ( )

( )

C A x

C yAy

.

..

правило обобщения (.-правило)

3) ( )

( )

A x C

yA y C

.

. .

правило введения . (.-правило)

4) Правило переименования связанной переменной. Связанную переменную формулы A можно заменить (в кванторе и во всех вхождениях в области действия квантора) другой переменной, не являющейся свободной в A. Понятия вывода, теоремы и доказательства определяются в исчислении предикатов точно так же, как и в любой аксиоматической теории. Теорема. Аксиомы исчисления предикатов – общезначимые форму-

лы. Теорема. Формула, получающаяся из общезначимой по любому из правил вывода 1–4, является общезначимой. Теорема. Любая выводимая в исчислении предикатов формула общезначима. Теорема. Исчисление предикатов непротиворечиво. Теорема Гёделя. Всякая общезначимая формула выводима в исчислении

предикатов. Теорема о дедукции. Если имеется вывод в исчислении предикатов формулы B из последовательности формул ., A, то можно построить вывод формулы A.B из последовательности формул . (символически: Если ., A.. B, то ...A.B), где . – набор некоторых формул A1, A2,..., An.

Применение логики предикатов к естественному языку

.xA(x) Для любого x (имеет место) A

A(x) при произвольном x

Для всех x (верно) A(x)

A(x), каково бы ни было x

Для каждого x (верно) A(x)

Всегда имеет место A(x)

Каждый обладает свойством A

Свойство A присуще всем

Всё удовлетворяет A

Любой объект является A

Всякая вещь обладает свойством A

.xA(x) Для некоторых x (имеет место) A(x)

Для подходящего x (верно) A(x)

Существует x, для которого (такой, что) A(x)

Имеется x, для которого (такой, что) A(x)

Найдется x, для которого (такой, что) A(x)

У некоторых вещей есть признак A

Хотя бы для одного x (верно) A(x)

Кто-нибудь относится к (есть)A

По крайней мере, один объект есть A

9.xA(x) Не для каждого x (верно) A(x)

Не при всяких x (верно) A(x)

A(x) оказывается истинным не для всех x

Не всё обладает свойством A

Не все суть A

A не всегда верно

.x¬A(x) Для всякого x неверно A(x)

A(x) всегда ложно

Ничто не обладает свойством A

Все суть не A

9.xA(x) Не существует x такого, что A(x)

Нет (никакого) x такого, что A(x)

A(x) не выполняется ни для какого x

Ничто не обладает свойством A

Никто не есть A

Неверно, что для некоторых x A(x)

.x¬A(x) Для некоторого x не(верно) A(x)

Что-то не обладает свойством A

Кто-то суть не A

Пример. Правильная формализация высказывания «Выгул кошек и собак

воспрещен» – 9.x((K(x).C(x)).B(x)) или .x((K(x).C(x)).¬B(x)). Но было бы

ошибкой переводить «На всех кошек и собак надлежит получить разрешение»

через .x((K(x).C(x)).P(x)), т.к. множество x таких что верно K(x).C(x) пусто.

Правильный перевод:

.x(K(x).P(x))..x(C(x).P(x)) или .x((K(x).C(x)).P(x)).

4.4. ИСЧИСЛЕНИЕ ОДНОМЕСТНЫХ ПРЕДИКАТОВ КАК

ИСЧИСЛЕНИЕ КЛАССОВ. ТЕОРИЯ КАТЕГОРИЧЕСКИХ

СУЖДЕНИЙ И СИЛЛОГИЗМОВ АРИСТОТЕЛЯ.

Совокупность предметов, на котором одноместный предикат принимает значение И, называется характеристическим классом. Используя понятие характеристического класса, можно установить соответствие между теорией множеств и исчислением одноместных предикатов. При этом операция конъюнкции двух предикатов будет соответствовать операции пересечения их характеристических классов, дизъюнкция – объединению, отрицание – дополнению и т.д. Заметим, что множество и класс – не эквивалентные понятия. Для каждого множества можно определить предикат, характеристический класс которого будет совпадать с этим множеством, однако не всякий характеристический класс – множество. Примером класса, не являющегося множеством, является класс Рассела (известный также, как парадокс брадобрея), определяемый пре-

дикатом: F(x)=x.x. Категорическим суждением в логике Аристотеля называется высказывание о двух классах. Всего выделяется четыре типа категорических суждений. Общеутвердительным называется высказывание вида «Все предметы класса P суть предметы класса Q». Общеутвердительное высказывание обозначает-

ся буквой A. Общеотрицательным называется высказывание вида «Никакие предметы класса P не суть предметы класса Q». Общеотрицательное высказывание обозначается буквой E. Частноутвердительным называется высказывание вида «Некоторые предметы класса P суть предметы класса Q». Частноутвердительное высказывание обозначается буквой I. Частноотрицательным называется высказывание вида «Некоторые предметы класса P не суть предметы класса Q». Частноотрицательное высказывание обозначается буквой O.

Пользуясь исчислением предикатов, категорические суждения можно формализовать следующим образом.

A. .x(P(x).Q(x))=.x(¬P(x).Q(x))=.x¬(P(x).¬Q(x))=10.x(P(x) .¬Q(x)),

E. .x(P(x).¬Q(x))=.x(Q(x).¬P(x))=.x(¬P(x).¬Q(x))=10.x(P(x).Q(x)),

I. .x(P(x).Q(x))=.x¬(¬P(x).¬Q(x))=10.x(¬P(x).¬Q(x))=10.x(P(x).¬Q(x)),

O. .x(P(x).¬Q(x))=10.x(P(x).Q(x)).

В исчислении предикатов легко проверяются законы формальной логики Аристотеля:

I. Законы отрицания категорических суждений.

¬A=O; ¬O=A; ¬E=I; ¬I=E.

II. Законы обращения категорических суждений (обращением называется перестановка мест классов P и Q).

E E. = , I I. = .

III. Законы логики.

A.I; E.O; ¬(A.E); ¬(E.A); ¬(I.O); ¬(O.I)

Категорическим силлогизмом называется конструкция из трех категорических суждений о трех классах, в которой третье суждение логически следует из двух первых. При этом первое суждение называется большой посылкой, второе – малой посылкой, а третье – заключением. Класс, присутствующий в большой и в малой посылках, называется средним. Будем обозначать его буквой P. Класс, присутствующий в большой посылке и в заключении, называется большим. Будем обозначать его буквой Q. Класс, присутствующий в малой посылке и в заключении, называется малым. Будем обозначать его буквой S. Силлогизм называется правильным, если истинность посылок всегда вызывает истинность заключения, независимо от содержания высказываний. Аристотель классифицировал все виды силлогизмов по типам (модусам) и выделил из всех модусов правильные. Все модусы Аристотель подразделил на 4 группы по расположению классов.

1)

PQ

SP

SQ

2)

QP

SP

SQ

3)

PQ

PS

SQ

4)

QP

PS

SQ

Поскольку категорические суждения бывают четырех типов, каждая группа силлогизмов содержит 64 различных модуса. Для запоминания, какие из них правильные, используют мнемонические имена.

Правильными являются следующие модусы:

В первой группе – Barbara, Celarent, Darii, Ferio.

Во второй группе – Cesare, Camestres, Festino, Baroco.

В третьей группе – Datisi, Ferison, Disamis, Bocado.

В четвертой группе – Fresison, Dimatis, Calemes.

Пользуются этими именами следующим образом. Гласные буквы подставляют в заданном этим именем порядке в шаблон группы модусов. Эти буквы означают тип категорического суждения. Например, построим силлогизм по модусу Barbara

PaQ Все люди смертны.

SaP Кай – человек.

SaQ Кай – смертен.

Проверить правильность модусов можно в исчислении предикатов. Отметим, что Аристотель и его последователи не признавали классов, в которых нет объектов (например, пустое множество). Поэтому в логике Аристотеля не 15 правильных модусов, а 19: в третьей группе добавляются модусы Darapti и Felapton,

а в четвертой – Bamalip и Fesapo, которые правильны при условии непустоты классов P, S и Q.

--------------------------------------------------------------------------------------------------------------------------------------------

Вопрос №15(Неформальные св-ва понятия алгоритма, алфавита, слова, терма)

Алгоритм(Мальцев)

1.Дискретность: Процесс последовательного построения величин идущий в дискретном времени так, что в 1-й момент задается исходная (конечная ) система величин, а далее система величин получается из предыдущей посредством определенных законов.

2. Детерминированность: система величин полученная в какой-то момент времени однозначно определяется с. в. полученной в предшествующий момент времени.

3. Элементарность шагов: закон получения последующих величин должен быть простым и локальным.

4. Направленность: если способ получения следующей величины из предыдущей не дает результата, то надо указать что будет результатом.

5. Массовость: начальная система величин должна выбираться из потенциально бесконечного множества величин.

Алгоритм(Роджерс)

1. Набор инструкций конечных размеров

2. Имеется вычислитель для работы с инструкциями и производства вычислений

3. Имеется возможность для выделения, запоминания, повторения шагов при вычислении

4. Если Р – набор инструментов, N – вычислитель, то взаимодействие: для любого поля (набора) вычисления происходят дискретно, по шагам, без аналоговых устройств.

5. Детерминированность.

6. Всегда начальная система величин должна быть конечной.

Функция вычислима, если существует алгоритм, который её вычисляет.

Терм – слово из символов.

Вопрос №16(Простейшие вычислимые функции, Оператор суперпозиции, Операторная форма)

Простейшие вычислимые функции

1. S(x)=x+1; Следование

2. O(x)=0; Нулевая

3. Выбор

1, 2, 3 – вычислимые по определению.

Оператор – схема вывода функции из уже имеющейся

Суперпозиции

Вопрос №17(Оператор примитивной рекурсии, Алгоритм, Операторная и термальная формы)

Вопрос №18(Класс ПРФ, ПРФ сложения и умножения)

Вопрос №19(Существование вычислимых не ПРФ)

Вопрос №20(Оператор минимизации, Класс ЧРФ)

Вопрос №21(Детерминант вычислимой функции, Алгоритм)

--------------------------------------------------------------------------------------------------------------------------------------------

Вопрос №22(Абстракция понятия процесса, Примеры процессов)

Забудем на время о компьютерах и программировании и вместо этого подумаем о вещах, которые нас окружают. Они действуют и вступают во взаимодействие с нами и друг с другом в соответствии со своими особенностями. Вспомним о часах, телефонах, настольных играх, торговых автоматах. Чтобы описывать поведение (работу) этих объектов, надо решить, какого рода события или действия нас заинтересуют, и выбрать для каждого из них подходящее название, или имя. В случае простого торгового автомата существуют два вида событий;

мон – опускание монеты в щель автомата,

шок – появление шоколадки из выдающего устройства.

В случае более сложного торгового автомата различных событий может быть больше:

n1 – опускание 1 пенни,

n2 – опускание монеты в 2 пенни,

мал – появление маленького коржика или булочки,

бол – появление большого коржика или булочки,

сд1–появление 1 пенни сдачи.

Заметим, что имя каждого события обозначает целый класс событий; отдельные вхождения события внутри одного класса разделены во времени. Аналогичное различие между классом и вхождением можно проследить на примере буквы «а», многочисленные вхождения которой в текст этой книги разделены в пространстве.

Множество имен событий, выбранных для конкретного описания объекта, называется его алфавитом. Алфавит счи­тается постоянным, заранее определенным свойством объекта. Участвовать в событии, выходящем за рамки его алфавита, для объекта логически невозможно – автомат по продаже шоколадок никогда не выдаст вам неожиданно игрушечный линкор. Обратное, впрочем, не обязательно. Машина, предназначенная для продажи шоколадок, может на самом деле этого не делать – возможно, потому что ее не загрузили, или она сломалась, или же просто никто не хочет шоколада. Но если уж решено, что «шок» входит в алфавит машины, то это имя останется там, несмотря на то, что соответствующее событие фактически никогда не происходит.

Обычно выбор алфавита влечет за собой сознательное упрощение: не рассматриваются многие действия и свойства, представляющие меньший интерес. Например, не описы­ваются цвет, вес и форма торгового автомата, равно как и такие весьма важные события в его жизни, как пополнение запаса шоколадок или разгрузка монетоприемника. Возмож­но, это делается из тех соображений, что эти детали не имеют (или не должны иметь) прямого отношения к пользователям автомата.

Считается, что конкретное событие в жизни объекта про­исходит мгновенно, т. е. является элементарным действием, не имеющим протяженности во времени. Протяженное, т. е. требующее времени, действие следует рассматривать как пару событий, первое из которых отмечает начало действия, а второе – его завершение. Продолжительность действия определяется интервалом между наступлением его события-начала и наступлением его события-завершения; в течение всего этого времени могут происходить другие события. Два протяженных действия могут перекрываться по времени, если начало каждого из них предшествует завершению другого.

Еще одно обстоятельство, от которого мы сознательно абстрагируемся, – это точная привязка событий ко времени. Преимуществом такого подхода является упрощение по­строений и рассуждений, которые к тому же можно приме­нить к физическим и вычислительным системам любой скоро­сти и производительности. В тех же случаях, когда временная привязка событий необходима по существу, соответствующее рассмотрение может быть проведено дополнительно к дока­зательству логической правильности построения. Независи­мость от времени всегда была решающим условием успеш­ного применения языков программирования высокого уровня.

Следствием исключения времени является то, что мы от­казываемся не только от ответов, то даже и от вопросов о том, происходит ли одно событие строго одновременно с другим. Когда совместность событий существенна (напри­мер, при синхронизации), мы отмечаем это, сводя их в одно -событие, или же позволяем совместным событиям происхо­дить в любом относительно друг друга порядке.

При выборе алфавита не обязательно делать различия между событиями, инициированными самим объектом (на­пример, «шок») или некоторым внешним по отношению объекту фактором (например, «мон»). Неупотребление по­нятия причинности ведет к значительному упрощению нашей теории и ее приложений.

Будем отныне употреблять слово процесс для обозначения поведения объекта постольку, поскольку оно может быть описано в терминах ограниченного набора событий, выбран­ного в качестве его алфавита. Введем следующие соглашения:

1. Имена событий будем обозначать словами, составлен­ными из строчных букв, например:

мон, шок, n1, n2,

а также буквами a, b, c, d, e.

2. Имена конкретных процессов будем обозначать сло­вами, составленными из прописных букв, например:

ТАП – простой торговый автомат,

ТАС – сложный торговый автомат,

а буквами P, Q, R (в законах) будем обозначать произволь­ные процессы.

3. Буквы x, у, z используются для переменных, обозначаю­щих события.

4. Буквы A, В, С используются для обозначения множества событий.

5. Буквы X, Y используются для переменных, обозначающих процессы.

6. Алфавит процесса P обозначается αР, например:

αТАП={мон, шок}

αТИС = {n7, n2, мал, бол, сд1}

Процесс с алфавитом А, такой, что в нем не происходит ни одно событие из Л, назовем СТОП_А. Этот процесс описывает поведение сломанного объекта: имея физическую способность участвовать в событиях из А, тот никогда ее не использует. Мы различаем объекты с различными алфави­тами, даже если эти объекты ничего не делают. Так, СТОП_αТАП мог бы выдать шоколадку, тогда как СТОП_αТАС никогда бы не выдал шоколадку, а только коржик. Покупатель знает это даже в том случае, когда ему неизвестно, что обе машины сломаны.

В заключение определим простую систему обозначений, которая поможет при описании объектов, уже обладающих способностью к некоторым действиям.

Вопрос №23(Описание процессов, Префиксная запись)

Пусть х – событие, a P – процесс. Тогда (х → P) (читается как "P за х")

описывает объект, который вначале участвует в событии х, а затем ведет себя в точности как Р. Процесс (х→Р) имеет по определению тот же алфавит, что и P; поэтому это обозначение можно использовать только при условии, что х при­надлежит тому же алфавиту. Более формально:

α (х → P) = αР, если х → αР

Примеры

X1. Простой торговый автомат, который поглощает монету и ломается:

(мон → СТОП_αТАП)

X2. Простой торговый автомат, который благополучно обслу­живает двух покупателей и затем ломается:

(мон → (шок → (мон → (шок → (СТОП_αТАС))))

В начальном состоянии автомат позволяет опустить монету, но не позволяет вынуть шоколадку. После же приема монеты щель автомата закрывается до тех пор, пока не будет вынута шоколадка. Таким образом, эта машина не позволяет ни опустить две монеты подряд, ни получить подряд две шоко­ладки.

В дальнейшем мы будем опускать скобки в случае линей­ной последовательности событий, как в примере X2, условив­шись, что операция → ассоциативна справа.

X3. Фишка находится в левом нижнем углу поля и может двигаться только вверх или вправо на соседнюю белую клетку:

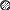
αФИШ ={вверх, вправо}

ФИШ = ( вправо → вверх → вправо → вправо → СТОП_αФИШ)

Заметим, что в записи с операцией → справа всегда стоит процесс, а слева – отдельное событие. Если P и Q – процессы, то запись P → Q синтаксически неверна. Правильный спо­соб описания процесса, который ведет себя сначала как P, а затем как Q, будет дан в гл. 4. Аналогично синтаксически неверной будет запись x → y, где x и у – события. Такой про­цесс надо было бы записать как х → (у → СТОП). Таким об­разом, мы тщательно разделяем понятия «событие» и «процесс», состоящий из событий – может быть, из многих, а мо­жет быть, ни из одного.

Вопрос №24(Рекурсивное описание процессов, Предваренная форма)

Префиксную запись можно использовать для полного опи­сания поведения процесса, который рано или поздно оста­навливается. Но было бы чрезвычайно утомительно пол­ностью выписывать поведение торгового автомата, рассчи­танного на долгую службу; поэтому нам необходим способ более сжатого описания повторяющихся действий. Было бы желательно, чтобы этот способ не требовал знать заранее срок жизни объекта; это позволило бы нам описывать объ­екты, которые продолжали бы действовать и взаимодейство­вать с их окружением до тех пор, пока в них есть необхо­димость.

Рассмотрим простейший долговечный объект – часы, у ко­торых только одна забота – тикать (их заводом мы сознательно пренебрегаем):

αЧАСЫ = {тик}

Теперь рассмотрим объект, который вначале издает един­ственный «тик», а затем ведет себя в точности как ЧАСЫ

(тик → ЧАСЫ)

Поведение этого объекта неотличимо от поведения исход­ных часов. Следовательно, один и тот же процесс описывает поведение обоих объектов. Эти рассуждения позволяют сформулировать равенство

ЧАСЫ = (тик → ЧАСЫ)

Его можно рассматривать как неявное задание поведения часов, точно так же как корень квадратный из двух может быть найден как положительное решение для х в уравнении

х = х² + х – 2

Уравнение для часов имеет некоторые очевидные след­ствия, которые получаются простой заменой членов на равные:

ЧАСЫ = (тик → ЧАСЫ) исходное уравнение

= (тик → (тик → ЧАСЫ)) подстановкой

= (тик → тик → тик → ЧАСЫ) аналогично

Это уравнение можно развертывать столько раз, сколько нужно, при этом возможность для дальнейшего развертыва­ния сохраняется. Мы эффективно описали потенциально бес­конечное поведение объекта ЧАСЫ как

тик → тик → тик ...

точно так же, как корень квадратный из двух можно пред­ставить в виде предела последовательности десятичных дро­бей 1.414… .

Такой метод «самоназывания», или рекурсивное опреде­ление процесса, будет правильно работать, только если в правой части уравнения рекурсивному вхождению имени про­цесса предшествует хотя бы одно событие. Например, рекур­сивное «определение» X = X не определяет ничего, так как решением этого уравнения может служить все что угодно. Описание процесса, начинающееся с префикса, называется предваренным. Если F(X) – предваренное выражение, содер­жащее имя процесса X, а A – алфавит X, то мы утверж­даем, что уравнение X = F(X) имеет единственное решение в алфавите А Иногда удобнее обозначать это решение выра­жением μX : A.F(X). Здесь X является локальным именем (связанной переменной) и может произвольно изменяться, поскольку

μХ : A.F(Х) = μY: A.F(Y).

Справедливость этого равенства следует из того, что решение для X уравнения X = F(X) является также решением для Y уравнения Y = F(Y),

В дальнейшем мы будем задавать рекурсивные определе­ния процессов либо уравнениями, либо с помощью μ-оператора в зависимости от того, что удобнее. В записи μX : A.F(X) мы часто будем опускать явное упоминание алфавита А, если это понятно из контекста или из содержания процесса.

Примеры

X1. Вечные часы

ЧАСЫ = μХ:{тик}. (тик X)

X2. Наконец-то простой торговый автомат, полностью удовлетворяющий спрос на шоколадки:

ТАП = (мон (шок ТАП))

Как уже пояснялось, это уравнение является лишь альтернативой более формального определения

ТАП = μХ:{мон, шок}. (мон (шок Х))

X3. Автомат по размеру монеты в 5 пенни

αPAЗM5А = {n5, сд2, cд1} РАЗМ5А = (n5 → сд2 → сд1 → сд2 → РАЗМ5А)

X4. Другой автомат по размену монет с тем же алфавитом}

РАЗМ5В = (n5 → сд1 → сд1 → сд1 → сд2 → РАЗМ5В)

Утверждение о том, что предваренное уравнение имеет решение, и это решение единственное, можно неформально доказать методом подстановки. Всякий раз, когда в правую часть уравнения производится подстановка на место каждого вхождения имени процесса, выражение, определяющее пове­дение процесса, становится длиннее, а значит, описывает больший начальный отрезок этого поведения. Таким путем можно определить любой конечный отрезок поведения про­цесса. А так как два объекта, ведущие себя одинаково вплоть до любого момента времени, ведут себя одинаково всегда, то они представляют собой один и тот же процесс. Те, кто счи­тает, что такие рассуждения непонятны или неубедительны, могут принять это утверждение как аксиому; со временем его важность и уместность станут очевидными. Более строгое до­казательство невозможно без точного математического опре­деления процесса. Это будет сделано в разд. 2.8.3. Приве­денное здесь описание рекурсии существенно опирается на понятие предваренности рекурсивного уравнёния. Смысл не­ предваренной рекурсии мы обсудим в разд. 3.8.

Вопрос №25(Оператор выбора, Начальное меню процесса)

Используя префиксы и рекурсию, можно описывать объ­екты, обладающие только одной возможной линией поведе­ния. Однако поведение многих объектов зависит от окружаю­щей их обстановки. Например, торговый автомат может иметь различные щели для 1- и 2-пенсовых монет; выбор одного из двух событий в этом случае предоставлен покупателю.

Если х и у – различные события, то (х Р | y Q) опи­сывает объект, который сначала участвует в одном из событий х, у. Последующее же поведение объекта описывается процессом P, если первым произошло событие х, или Q, если первым произошло событие у. Поскольку х и у – различные события, то выбор между P и Q определяется тем, какое из событий в действительности наступило первым. Требование неизменности алфавитов по-прежнему остается в силе, т. e.

α (х Р | y Q) = αР

если {x, y} ⊆ αP и αP = αQ. Вертикальную черту | следует читать как "или":"Р за х или Q за у".

Примеры

X1. Возможные перемещения фишки на поле описываются процессом

(вверх → СТОП | вправо → вправо → вверх → СТОП)

X2. Автомат с двумя вариантами размена монеты в 5 пенни (ср. с примерами 1.1.2 X3 и X4, где выбора нет):

РАЗМ5C = n5 →( сд1 → сд1 → сд1 → сд2 → РАЗМ5C | сд2 → сд1 → сд2 → РАЗМ5C)

Выбор осуществляется покупателем.

X3. Автомат, предлагающий на выбор шоколадку или ириску;

ТАШИ = μХ . мон → (шок → Х | ирис → Х)

X4. Более сложный автомат, предлагающий различные това­ры различной стоимости и дающий сдачу:

ТАС = (n2 → (бол → ТАС | мал → сд1 → ТАС) |

n1 → (мал → ТАС | n1 → (бол → ТАС | n1 → СТОП)))

Как и многие сложные механизмы, этот автомат имеет в своей конструкции изъян. Часто бывает проще изменить инструкцию для пользователя, чем вносить исправления в го­товую разработку, и поэтому мы снабдим наш автомат предупреждением:

«ВНИМАНИЕ: не опускайте три монеты подряд!»

X5. Автомат, доверяющий покупателю сначала попробовать шоколад, а заплатить потом. Нормальная последовательность событий тоже допускается:

ТАДОВЕР = μX.. (мон шок Z | шок мон X)

X6. Чтобы не возникало убытков, за право пользоваться ТАДОВЕР взимается предварительная плата

ТАП2 = (мон ТАДОВЕР)

Эта машина позволяет опустить последовательно до двух монет, после чего последовательно получить до двух шоколадок; она не выдает ни на шоколадку больше заранее опла­ченного количества.

X7. Процесс копирования состоит из следующих событий:

вв.0 – считывание нуля из входного канала,

вв.1 – считывание единицы из входного канала,

выв.0 – запись нуля в выходной канал,

выв.1 – запись единицы в выходной канал.

Поведение процесса состоит из повторяющихся пар событий. На каждом такте он считывает, а затем записывает один бит.

КОПИБИТ = μХ.. (вв.0 → выв.0 → Х | вв.l → выв.1 → Х)

Заметим, что этот процесс предоставляет своему окружению выбор того, какое значение следует ввести, но сам решает, какое значение вывести. В этом будет состоять основное различие между считыванием и записью в нашей трактовке вза­имодействия в гл. 4.

Определение выбора легко обобщить на случай более чем двух альтернатив, например:

(x → P | y → Q | … | z → R)

Заметим, что символ выбора | не является операцией над процессами; для процессов P и Q запись P | Q будет синтаксически неверной. Мы вводим это правило, чтобы избежать необходимости выяснять смысл записи (х → P) | (у → Q), в которой безуспешно предлагается выбор первого события. Эта проблема решается в разд. 3.3 ценой введения недетерминизма. Между тем, если х, у, z – различные события, запись

(x → P | y → Q | … | z → R)

следует рассматривать как один оператор с тремя аргумен­тами P, Q, R. При этом она не будет эквивалентна записи

((x → P) | (y → Q) | … | (z → R))

которая синтаксически неверна,

В общем случае если В – некоторое множество событий, а Р(x) – выражение, определяющее процесс для всех раз­личных x из В, то запись

(x:B → P(x))

определяет процесс, который сначала предлагает на выбор любое событие у из В, а затем ведет себя как P(y). Запись следует читать как «P от х за х из B». В этой конструкции х играет роль локальной переменной, и поэтому

(х:B →P(х)) = (y:B →P(y))

Множество В определяет начальное женю процесса, потому что в нем предлагается набор действий, из которого осуще­ствляется первоначальный выбор.

Пример

X8. Процесс, который в каждый момент времени может уча­ствовать в любом событии из своего алфавита А:

αИСП_А = А

ИСП_А = (х: А → ИСП_А)

В особом случае, когда в начальном меню содержится лишь одно событие e,

(х:{е} →P(х)) = (e → P(e))

потому что е является единственным возможным начальным событием. В еще более специальном случае, когда начальное меню пусто, вообще ничего не происходит, и поэтому

(х:{ } → Р(х)) = (y:{ } → Q(y)) = СТОП

Двуместный оператор выбора | можно определить и в более общих обозначениях:

(a → P | b → Q) = (x:B → R(x)) где B={a, b}, а R(x) = if х = а then P else Q.

Аналогичным образом можно выразить выбор из трех и более альтернатив. Итак, мы сумели сформулировать выбор, префик­сы и СТОП как частные случаи записи обобщенного оператора выбора. Это нам очень пригодится в разд. 1.3, где будут сформулированы общие законы, которым подчиняются процессы, и в разд. 1.4, посвященном реализации процессов.

Вопрос №26(Графическое представление процесса, Состояние процесса)

Иногда процесс полезно представить графически в виде древовидной структуры с помощью кружков-вершин, соединенных стрелками-дугами. Следуя традиционной терминоло­гии машин, обладающих внутренними состояниями, вершины представляют состояния процесса, а дуги – переходы между ними. Корневая вершина дерева (изображаемая обычно ввер­ху страницы) соответствует начальному состоянию; от нее процесс движется вниз по стрелкам. Каждая дуга помечена именем события, которое соответствует данному переходу. Все дуги, ведущие из одной вершины, должны иметь различ­ные метки.

Примеры (1.1.1 Х1, Х2; 1.1.3 Х3)

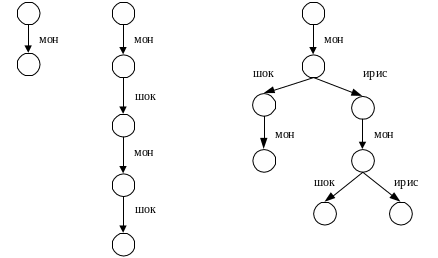
В этих трех примерах каждая ветвь каждого дерева окан­чивается состоянием СТОП, которое изображается вершиной без выходных дуг. Для представления процессов, обладаю­щих неограниченным поведением, необходимо еще одно условное обозначение, а именно: непомеченная дуга, ведущая из висячей вершины назад к некоторой вершине дерева. Условимся, что когда процесс достигает вершины у основания этой дуги, он мгновенно переходит назад к вершине, на ко­торую указывает дуга.

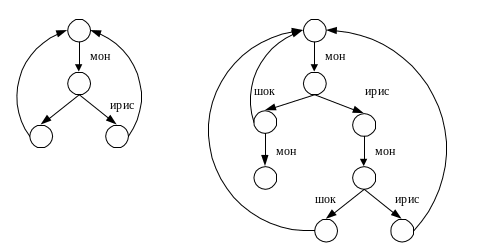
Очевидно, что два этих различных рисунка иллюстри­руют в точности один и тот же процесс (1.1.3 Х3 ¹). Одна из слабостей графического представления, однако, состоит в том, что доказать такое равенство графически очень трудно.

Другая проблема рисунков – это то, что с их помощью нельзя представить процесс с очень большим или бесконеч­ным числом состояний, например CT₀:

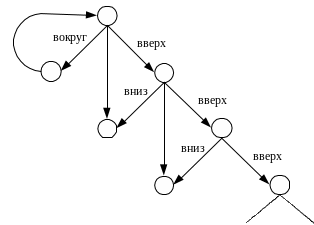
Чтобы нарисовать эту картину целиком, никогда не хватит места. Да и на рисунок для объекта, обладающего «всего» 65536 состояниями, потребуется немало времени.

Вопрос №27(Понятие протокола, Поведение процесса)

Протоколом поведения процесса называется конечная по­следовательность символов, фиксирующая события, в которых процесс участвовал до некоторого момента времени. Пред­ставьте себе наблюдателя с блокнотом, который следит за процессом и записывает имя каждого происходящего собы­тия. У нас есть все основания не учитывать возможности одно­временного наступления двух событий; даже если это случится, наблюдателю все равно придется записать их одно за другим, и порядок, в котором записаны события, не будет иметь значения.

Мы будем обозначать протокол последовательностью сим­волов, разделенной запятыми и заключенной в угловые скобки:

<x, у> состоит из двух событий – х и следующего за ним у.

<x> состоит из единственного события x.

<> пустая последовательность, не содержащая событий.

Примеры

X1. Протокол простого торгового автомата ТАП (1.1.2 Х2) в момент завершения обслуживания первых двух покупателей:

<мон, шок, мон, шок>

Х2. Протокол того же автомата перед тем, как второй поку­патель вынул свою шоколадку:

<мон, шок, мон>

Понятие завершенной сделки недоступно ни процессу, ни его наблюдателю. Голод ожидающего клиента и готовность автомата его удовлетворить не входит в алфавит процесса и не могут быть зафиксированы и занесены в протокол.

Х3. Перед началом работы процесса блокнот наблюдателя пуст. Это изображается пустым протоколом <> – самым ко­ротким из всех возможных протоколов любого процесса.

Х4. Сложный торговый автомат ТАС(1.1.3. Х4) имеет семь различных протоколов длины два и менее:

<>

<n2> <n1>

<n2, бол > <n2, мал > <n1, n1> <n1, мал >

Из четырех протоколов длины два для данного устройства фактически может произойти только один. Его выбор по сво­ему желанию осуществляет первый покупатель.

Х5. Протокол ТАС, если первый покупатель нарушил инструк­цию: <n1, n1, n1>. Сам протокол не фиксирует поломку авто­мата. На нее указывает лишь тот факт, что среди всех воз­можных протоколов этой машины не существует такого, который являлся бы продолжением данного, т. е. не сущест­вует такого х, что <n1, n1, n1,x> является возможным протоколом ТАС. Покупатель может волноваться, негодовать; наблю­датель– нетерпеливо ожидать, держа карандаш наготове, но отныне не произойдет ни одно событие, и ни один символ не будет записан в блокнот. Окончательное право распорядиться судьбой покупателя и машины не входит в выбранный нами алфавит.