МЕТОДЫ МАТЕМАТИЧЕСКОЙ ФИЗИКИ
Лектор – д.т.н., профессор
Краснопевцев Евгений Александрович
Основная тема курса
Ортонормированные базисы функций
Практическая значимость курса –
разложение функций по ортонормированному базису упрощает решение физических и технических задач,
результаты получают наглядный физический смысл.
Разделы курса
Преобразование Фурье.
Сингулярные функции:
дельта-функция,
гребенчатая функция,
функция Хевисайда,
функция знака,
прямоугольная функция,
функция sinc,
треугольная функция.
Гамма- и бета-функции Эйлера.
Дифференциальные уравнения второго порядка.
Классические ортогональные полиномы:
Эрмита,
Лагерра,
Лежандра,
Чебышева.
Сферические функции.
Функции Бесселя.
Функция Грина.
Дифференциальные уравнения с частными производными.
Контрольные мероприятия
1. Индивидуальные задания 1, 2, 3 (4-ая, 9-ая, 14-ая недели).
2. Коллоквиум (в конце семестра).
3. Экзамен для группы РН, зачет для групп РМ, РМ7, РП, РЭ.
Ортонормированные базисы
Ортогональные координаты применяются во всех разделах физики и техники, где используются вектора. В результате:
упрощается решение задачи,
результаты выражаются через проекции,
и получают наглядный смысл.
Декартовы координаты ввел Декарт в 1637 г.
Рене Декарт (1596–1650)
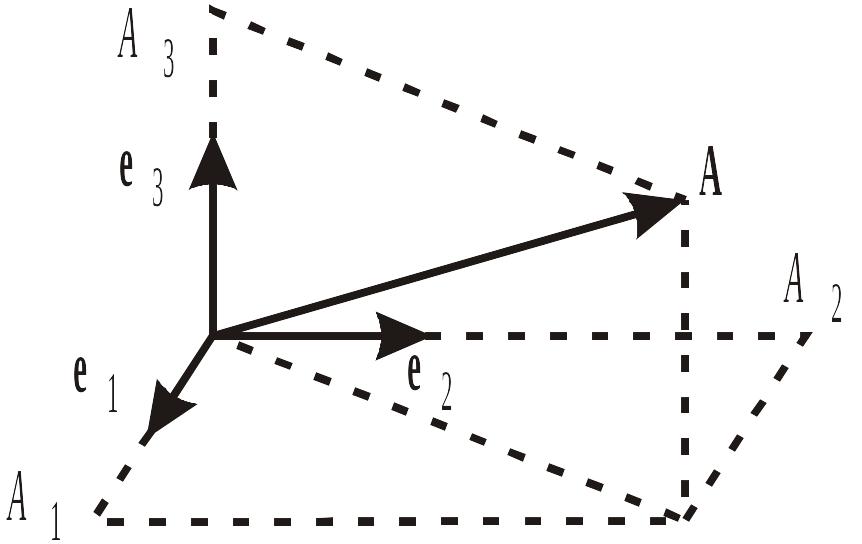
Где
– орты
– единичные, взаимно перпендикулярные
вектора;
– проекции
вектора
;
– скалярное
произведение;
– составляющие
вектора.
ВекторнЫе пространствА
Декартова система координат послужила основой для введения векторного пространства.
Векторное пространство – множество векторов, для которых определено скалярное произведение.
Размерность пространства – число независимых векторов, через сумму которых можно выразить, то есть разложить, произвольный вектор этого пространства.
3-мерное пространство
Базис ортов
Произвольный трехмерный вектор разлагается по трем ортам, образующим базис:
,
.
Скалярное произведение векторов
,
,
.
Если
угол
,
то вектора ортогональны
.
Норма
вектора
.
Вектор
нормирован, если
.
Условие ортонормированности базиса – вектора базиса взаимно ортогональны и нормированы
.
(0.1)
Символ Крόнекера
(0.2)
ввел Крóнекер в 1866 г.
Леопольд Крóнекер (1823–1891)
N-мерное пространство
Базис
,
,
ортонормирован
.
Разложение
вектора на
составляющие
.
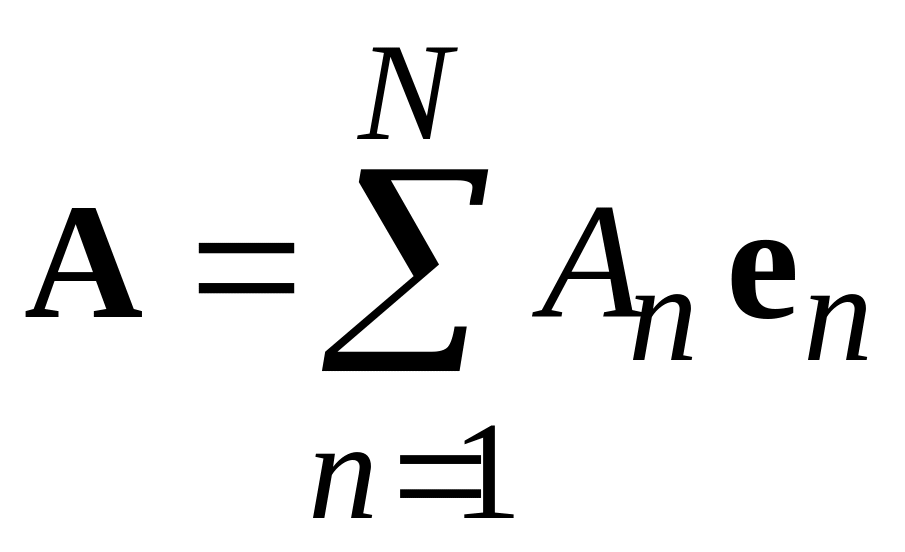(0.3)
Проекция
вектора на орт
.
(0.4)
Теорема Пифагора
– квадрат модуля вектора равен сумме квадратов его проекций на ортогональные оси. Доказывается подстановкой (0.3) и использованием ортонормированности базиса.
Гильбертово пространство с дискретным базисом
От пространства векторов переходим к пространству функций.
Гильбертово пространство – множество комплексных, квадратично интегрируемых функций, для которых определено скалярное произведение. Ввел Гильберт в 1910 г.
Давид Гильберт (1862–1943)
Базис ортов
,
,
N – размерность пространства – конечное или бесконечное число;
–комплексная,
квадратично интегрируемая функция,
определенная на интервале аргумента
.
Скалярное произведение определяется в виде
,
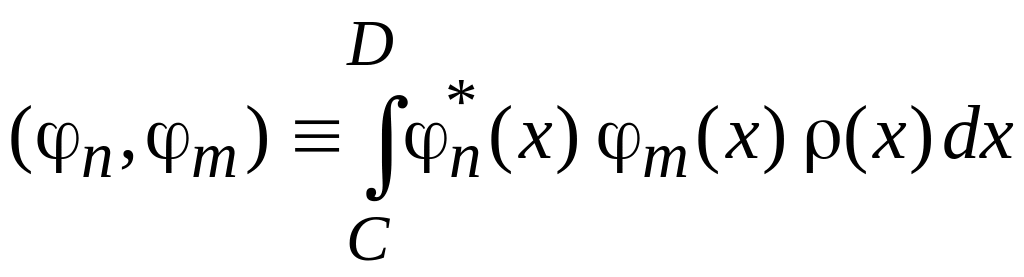(0.5)
где
– вещественная весовая
функция;
– комплексно сопряженная функция.
Комплексное сопряжение
вещественное
число
;
мнимая
единица
,
;
формула
Эйлера
,
,
,
,
.
Формулу получил Эйлер в 1740 г.
Леонард Эйлер (1707–1783)
Комплексное
число
,
;
квадрат
модуля числа
;
.
Условие ортонормированности базиса
.
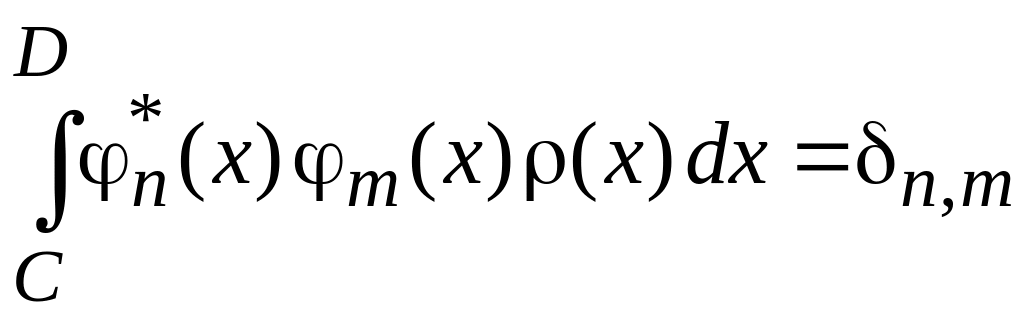(0.6)
Разложение функции по базису
,
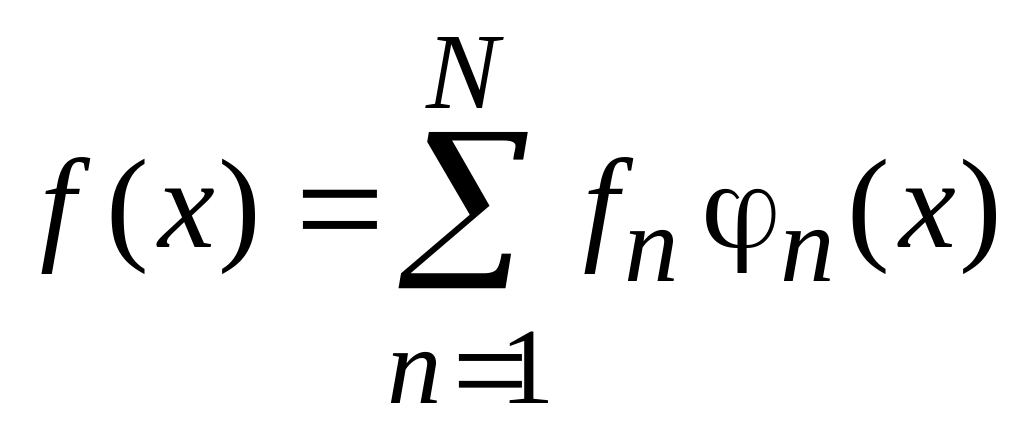(0.7)
где
– множество проекций, или спектр
функции
f(x).
Проекция
функции
на орт
.
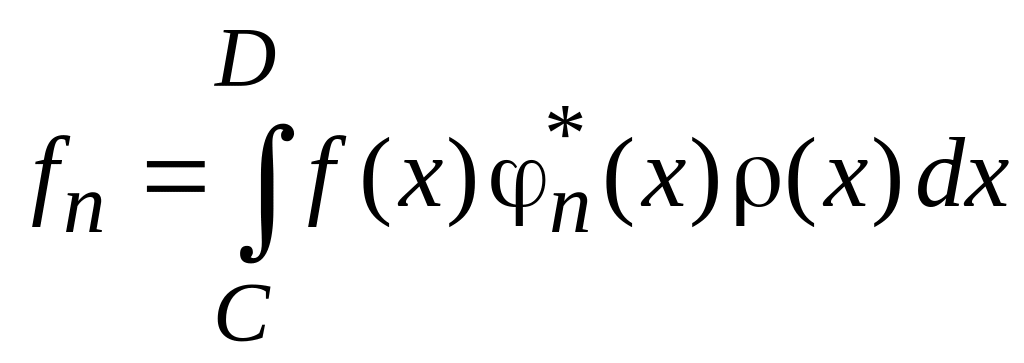(0.8)
Подстановка (0.8)→(0.7) дает тождество
,
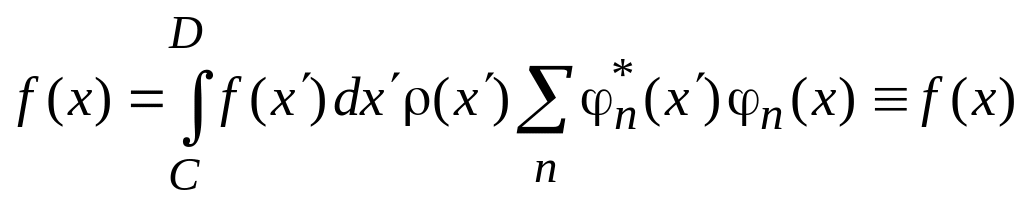если базис полон.
Условие полноты базиса
,
(0.9)
где
– дельта-функция,
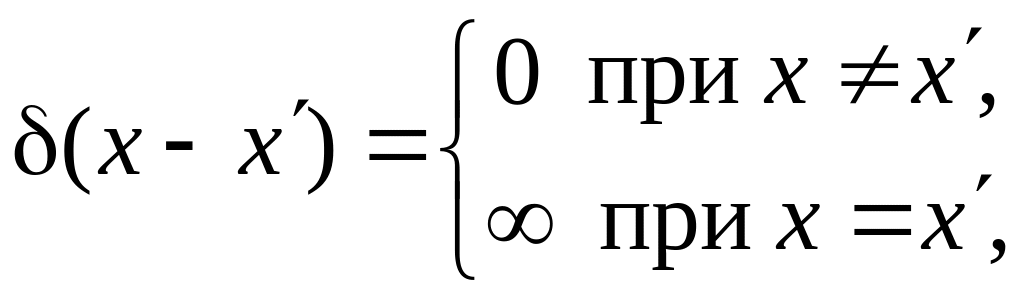
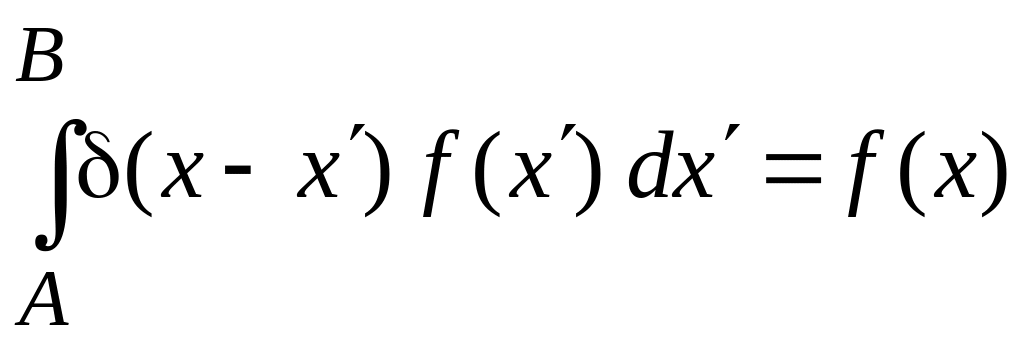– фильтрующее
свойство.
Теорема Парсеваля – аналог теоремы Пифагора в пространстве функций
,
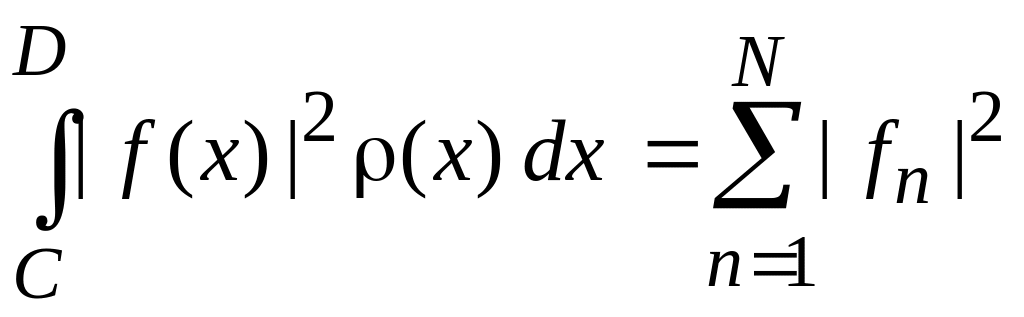(0.10)
где
,
.
Теорема доказывается подстановкой
(0.7) и использованием (0.9).
Теорему получил Мари-Антуан Парсеваль (1755–1836) в 1799 г.