Оптическое преобразование Фурье

Спектрометр – анализатор частот Анализатор длин волн

На призму с дисперсией падает Когерентная волна падает

волна с зависимостью на плоский транспарант с

от времени . коэффициентом пропускания .

Преобразование призмой: Преобразование линзой:

время → частота, координата → волновое число,

, ,

– распределение амплитуд – распределение амплитуд

по углам и частотам. в фокальной плоскости

, ,

Теоремы Фурье

Линейность преобразования

. (1.5)

Масштабное преобразование аргумента функции

. (1.6)

Доказательство: Из (1.1)

.

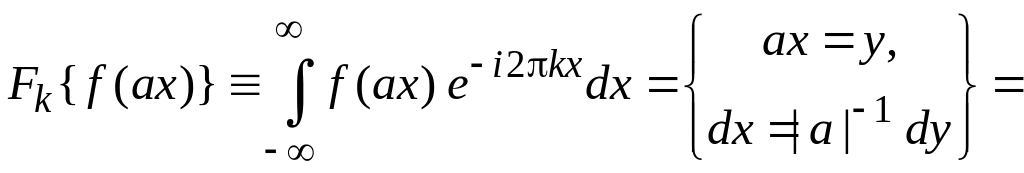
Функция Гаусса

, .

При масштабном преобразовании с – сжатие по x в 2 раза (переход от сплошной линии к пунктирной), растяжение по k и уменьшение амплитуды в 2 раза.

Инверсия аргумента

Из (1.6) при

. (1.7)

Четности функции и образа совпадают.

Теорема о частотной полосе

, (1.8)

где дисперсии

;

.

Уменьшение пространственной протяженности функции приводит к увеличению ее частотной протяженности , и наоборот.

Равенство в (1.8) выполняется для функции Гаусса

,

,

, ,

.

Смещение аргумента

. (1.9)

Доказательство: Из (1.1)

.

Фазовый сдвиг

. (1.10)

Доказательство: Из (1.1)

.

Комплексное сопряжение

, (1.11)

Доказательство: Из (1.1)

,

.

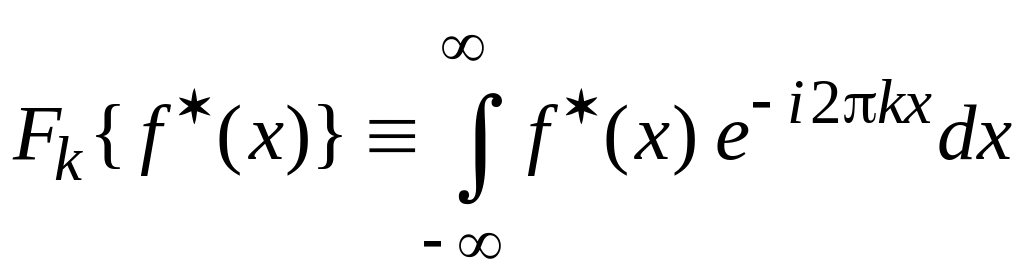Из (1.7) и (1.11)

,

получаем:

если – вещественная и четная, то вещественная;

если – вещественная и нечетная, то мнимая;

если – мнимая и четная, то мнимая;

если – мнимая и нечетная, то вещественная.

Теорема Парсеваля

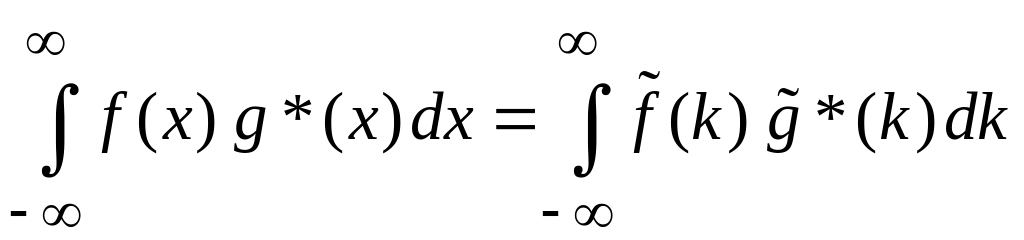. (1.14)

В физике выражает закон сохранения энергии и вероятности при преобразовании Фурье.

Доказательство: Из (1.2) и (1.1) с заменой порядка интегрирований

= .

Обобщенная теорема Парсеваля

. (1.15)

Ортонормированность базиса и его образа

Если функции ортонормированны

, (1.16)

то их фурье-образы также ортонормированны

. (1.17)

В (1.14) полагаем и .

Интегральная теорема – прямое и обратное преобразования восстанавливают непрерывную функцию

,

. (1.20)

Доказательство: Из (1.2) и (1.1) с заменой порядка интегрирований

,

где использовано

.

Следовательно, для непрерывной функции

, . (1.20а)

Теорема о парах функций и

Если

,

то

. (1.21)

Доказательство: Используем (1.1), заменяем аргумент

.

Сравниваем с (1.2) после замены: , , и получаем (1.21).