Таким образом, восстановлен только многочлен третьей степени (по заданной точности ε), который имеет вид
P3(x):= −0.933333 x3 + 3.388 x2 −8.211147 x + 9.999974 .
Это многочлен для интерполяции вперед, его можно употреблять для нахождения приближенных значений функции в верхней половине таблицы конечных разностей M 2. Например, P3(0.05) = 9.59 , P3(0.09) = 9.263. Аналогичную формулу для интерполяции на-
зад можно легко получить на основе приведенного материала. Желающие могут проделать это самостоятельно.
2.12. Интерполяционные формулы Гаусса, Стирлинга и Бесселя
Формулы Гаусса . Выпишем подробно таблицу конечных разностей для того, чтобы отмечать задействованные элементы этих таблиц в далее рассматриваемых формулах.
x y
x−4 y−4
x−3 y−3
x−2 |
y−2 |
|
|
y |
|
|
|
2 y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y−4
2 y−4
y−3
2 y−3
|
|
3 y |
|
|
4 y |
|
|
5 y |
|
|
6 y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 y−4 
4 y−4 
|
|
|
|
|
|
y−2 |
|
|
|
|
|
|
3 y−3 |
|
|
|
|
|
|
5 y−4 |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
x−1 |
|
y−1 |
|
|
|
|
|
2 y−2 |
|
|
|
|
|
|
4 y−3 |
|
|
|
|
|
6 y−4 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
y−1 |
|
|
|
|
|
|
3 y−2 |
|
|
|
|
|
|
|
5 y−3 |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
x0 |
|
y0 |
|
|
|
|
|
2 y−1 |
|
|
|
|
|
|
4 y−2 |
|
|
|
|
|
|
6 y−3 |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
y0 |
|
|
|
|
|
3 y−1 |
|
|
|
|
|
|
5 y−2 |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
x |
|
y |
|
|
|
|
|
2 y |
0 |
|
|
|
|
|
|
4 y |
−1 |
|
|
|
|
|
|
6 y |
−2 |
|
|||
|
1 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
y |
|
|
|
|
|
|
3 y |
0 |
|
|
|
|
|
|
|
5 y |
−1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
2 |
|
y |
2 |
|
|
|
|
|
2 y |
1 |
|
|
|
|
|
|
4 y |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
y |
2 |
|
|
|
|
|
|
3 y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
x3 |
|
y3 |
|
|
|
|
2 y2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
y3 |
x4 |
y4 |
- вторая интерполяционная формула Гаусса, - первая интерполяционная формула Гаусса, - формула Бесселя.
Первая интерполяционная формула Гаусса для интерполяции вперед имеет вид
Карл Фридрих Гаусс (1777-1855) - немецкий математик, астроном и геодезист.
57
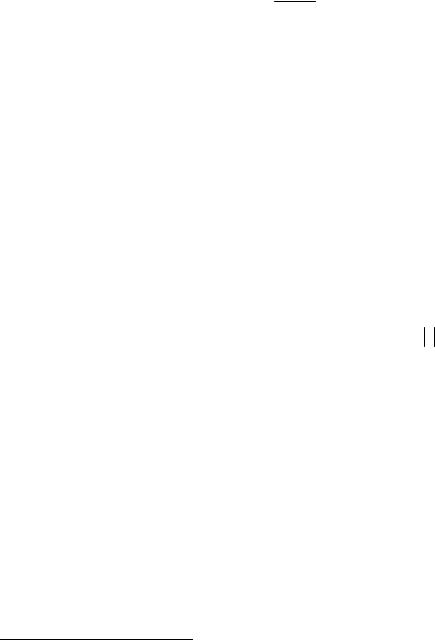
P(x)= y0 + |
|
y0 |
q + |
2 y−1 |
|
q(q −1)+ |
3 y−1 |
(q −1)q(q +1)+ |
4 y−2 |
(q − 2)(q −1)q(q +1)+ |
|
|||||
1! |
2! |
3! |
|
4! |
|
|||||||||||
|
5 y |
|
|
|
|
|
|
2n−1 y−(n−1) |
|
|
|
|||||
+ |
(q |
− 2)(q −1)q(q +1)(q + 2)+... + |
|
(q − n +1)(q − n + 2)...(q + n −1)+ |
(2.12.1) |
|||||||||||
5!−2 |
|
|
||||||||||||||
|
(2n −1)! |
|||||||||||||||
|
|
|
|
|
|
|
|
2n y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ |
|
−n |
(q − n)(q − n +1)...(q + n −1). |
|
|
|||||
|
|
|
|
|
|
|
(2n)! |
|
|
|||||||
Формулы Гаусса применяются для интерполирования в середине таблицы вблизи точки x0 . При этом формула (2.12.1) применяется при x > x0 , а формула (2.12.2) - вторая ин-
терполяционная формула Гаусса - при x < x0 .
P(x)= y0 + |
y−1 |
q + |
2 y−1 |
q(q +1)+ |
3 y−2 |
(q −1)q(q +1)+ |
4 y−2 |
(q −1)q(q +1)(q + 2)+ |
|
||||
|
2n−1 y |
1! |
|
2! |
|
3! |
|
2n y |
4! |
|
|
||
+ ... + |
−n |
(q − n +1)(q − n + 2)...(q + n −1)+ + |
−n |
(q − n +1)(q − n + 2)...(q + n), |
(2.12.2) |
||||||||
(2n −1)! |
(2n)! |
||||||||||||
q= x −h x0 .
Вобеих формулах используются разности, расположенные вблизи середины таблицы
(они помечены). Остаточный член формул (2.12.1) и (2.12.2) может быть записан в виде
R2n |
= |
h 2n+1 f (2n+1)(ζ) |
q(q 2 |
− 12 )(q 2 − 22 )...(q 2 − n 2 ), ζ (a, b), x0 , x±1 ,..., x±n (a, b). |
(2.12.3) |
|
|||||
|
|
(2n + 1)! |
|
|
|
Интерполяционная формула Стирлинга представляет собой среднее арифметическое (2.12.1) и (2.12.2), то есть среднее арифметическое первой и второй формулы Гаусса:
P(x)= y0 + |
y + y |
|
|
|
2 y |
|
q |
2 |
+ |
3 y + |
3 y |
|
(q |
2 |
−1 )q + |
4 y |
|
(q |
2 |
−1 )q |
2 |
+ |
|
|
|
||||||||||||||||
|
0 |
2 |
|
|
|
−1 |
q + 2! |
−1 |
2 3! |
|
−1 |
4! |
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−2 |
|
|
|
2 |
|
|
|
−2 |
|
|
2 |
|
|
|
|
|
|
||||||||
5 y |
−3 |
+ |
5 y |
−2 |
|
2 |
|
|
2 |
|
|
|
2 |
2 |
|
|
|
|
|
2n−1 y−n + |
2n−1 y−(n−1) |
|
2 |
|
|
|
2 |
|
2 |
|
2 |
|
|
|
2 |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
[q |
−(n −1) ](q |
|
|
|
|
|
|
||||||||||||||
+ |
2 5! |
|
|
(q |
|
− |
2 |
|
)q(q |
|
−1 )+... + |
|
|
|
|
|
|
−n |
|
)...q |
|
+ |
(2.12.4) |
||||||||||||||||||
|
|
|
|
|
|
2 (2n −1)! |
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
+ |
2n y−n |
[q2 −(n −1)2 ]...(q2 −12 )q2. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
(2n)! |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
Остаточный член этой формулы имеет тот же вид, что и для формул Гаусса, то есть вид (2.12.3). Формула (2.12.4) применяется для интерполирования в середине таблицы при зна-
чениях q , близких к нулю. Практически ее используют при q ≤ 0.25.
Интерполяционная формула Бесселя имеет вид: |
|
|
|
|||||||||||||||
|
y |
0 |
+ y |
|
|
|
1 |
|
2 y |
−1 |
+ 2 y |
0 |
|
3 y |
|
|
1 |
|
P(x)= |
|
1 |
+ |
y0 |
q − |
|
+ |
|
|
q(q −1)+ |
|
−1 |
(q −1) q − |
|
q + |
|||
|
|
2 |
|
2 2! |
|
3! |
2 |
|||||||||||
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|||||
4 y−2 + |
4 y−1 |
(q − 2)(q |
−1)q(q +1)+... + |
|
2n y−n + 2n y−n+1 |
q(q −1)(q +1)...(q + n −1)+ |
|
||||||||
+ |
2 4! |
|
|
|
|
(2.12.5) |
|||||||||
|
|
|
2 (2n)! |
||||||||||||
|
|
|
|
|
2n+1 y |
−n |
|
|
1 |
|
|
|
|
||
|
|
+ |
|
|
|
|
q − |
2 |
q(q −1)(q +1)(q −2)(q + 2)...(q −n)(q + n −1). |
|
|||||
|
|
|
|
|
|
|
|
||||||||
|
|
|
(2n +1)! |
|
|
|
|
|
|||||||
Ее остаточный член можно записать в виде |
|
|
|||||||||||||
R2n = |
h2n+2 f (2n+2) |
(ζ) |
q(q2 |
−12 )(q2 − 22 )...(q2 |
− n2 )(q − n −1), |
ζ (a, b), x0 , x±1 ,..., x±n (a, b). |
(2.12.6) |
||||||||
(2n + 2)! |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
Формула Бесселя используется для интерполирования в середине таблицы при значе- |
||||||||||||||
ниях |
q , близких к 0.5, практически при 0.25 ≤ q ≤ 0.75. Наиболее простой вид имеет фор- |
||||||||||||||
мула |
(2.12.5) при q = 0.5, так как все члены, содержащие разности нечетного порядка, про- |
||||||||||||||
Джемс Стирлинг (1692-1770) - английский математик.
Фридрих Вильгельм Бессель (1784-1846) - немецкий астроном и геодезист.
58
падают. Этот специальный случай формулы Бесселя называют формулой интерполирования на середину. Ее обычно используют для уплотнения таблиц. Общая особенность формул (2.12.1), (2.12.2), (2.12.4) и (2.12.5) заключается в том, что слагаемые в них убывают значительно быстрее, чем в формулах Ньютона, поэтому для достижения заданной точности нужно меньше вычислений.
Пример. Используя формулу Бесселя, уплотнить таблицу значений функции y = f (x) в два раза.
i |
x |
f (x) |
-2 |
2.0 |
1.5906 |
-1 |
2.1 |
1.7455 |
0 2.2 1.9141
1 |
2.3 |
2.0978 |
2 2.4 2.2981
3 2.5 2.5167
y |
2 y |
3 y |
4 y |
1549 |
|
|
|
|
137 |
|
|
1686 |
|
14 |
|
|
151 |
|
1 |
1837 |
|
15 |
|
|
166 |
|
2 |
2003 |
|
17 |
|
|
183 |
|
|
2186 |
|
|
|
59