
- •1. ЭЛЕМЕНТАРНАЯ ТЕОРИЯ ПОГРЕШНОСТЕЙ; ВЫЧИСЛИТЕЛЬНЫЕ ЗАДАЧИ, МЕТОДЫ И АЛГОРИТМЫ
- •1.1. Источники и классификация погрешностей результата численного эксперимента
- •1.2. Погрешности чисел
- •1.3. Погрешности арифметических операций
- •1.4. Погрешности функций
- •1.5. Особенности машинной арифметики
- •1.6. Лабораторная работа № 1. Определение абсолютной и относительной погрешностей приближенных чисел. Оценка погрешностей результата
- •1.7. Корректность вычислительной задачи
- •1.8. Обусловленность вычислительной задачи
- •1.9. Вычислительные методы, их классификация
- •2. ПРИБЛИЖЕНИЕ ФУНКЦИЙ
- •2.1. Задача приближения функций
- •2.2. Интерполяция обобщенными многочленами
- •2.3. Полиномиальная интерполяция. Многочлен Лагранжа
- •2.4. Погрешность интерполяции
- •2.5. Конечные разности и их свойства
- •Доказательство
- •2.6. Разделенные разности и их свойства
- •2.9. Лабораторная работа № 2. Интерполирование и экстраполирование данных. Интерполяционный многочлен Лагранжа
- •2.10. Интерполяционный многочлен Ньютона с конечными разностями
- •2.11. Лабораторная работа № 3. Интерполирование и экстраполирование данных. Интерполяционный многочлен Ньютона
- •2.12. Интерполяционные формулы Гаусса, Стирлинга и Бесселя
- •3. МЕТОД НАИМЕНЬШИХ КВАДРАТОВ И СПЕЦИАЛЬНЫЕ ИНТЕРПОЛЯЦИОННЫЕ МНОГОЧЛЕНЫ
- •3.1. Постановка задачи и вывод формул метода наименьших квадратов
- •3.3. Глобальная полиномиальная интерполяция
- •3.4. Чувствительность интерполяционного многочлена к погрешностям входных данных
- •3.5. Многочлены Чебышева
- •3.6. Решение задачи минимизации оценки погрешности
- •3.8. Лабораторная работа №5. Экономизация степенных рядов
- •3.9. Локальная интерполяция
- •3.10. Сплайны, их свойства и построение
- •3.11. Погрешность приближения кубическими сплайнами
- •3.13. Тригонометрическая интерполяция. Дискретное преобразование Фурье и его реализация на ЭВМ
- •3.14. Матричная форма записи дискретного преобразования Фурье (ДПФ)
- •3.15. Алгоритм реализации ДПФ
- •3.16. Пример реализации алгоритма ДПФ при
- •3.17. Лабораторная работа № 7. Дискретное преобразование Фурье
- •4. ЧИСЛЕННОЕ ДИФФЕРЕНЦИРОВАНИЕ И ЧИСЛЕННОЕ ИНТЕГРИРОВАНИЕ
- •4.1. Простейшие формулы численного дифференцирования для первой производной
- •4.2. Формулы численного дифференцирования для второй производной
- •4.3. Формулы численного дифференцирования, основанные на интерполяции алгебраическими многочленами
- •4.4. Обусловленность формул численного дифференцирования
- •4.5. Простейшие квадратурные методы численного интегрирования
- •4.6. Оценка погрешностей простейших квадратурных формул
- •4.7. Квадратурные формулы интерполяционного типа
- •4.8. Квадратурные формулы Гаусса
- •4.9. Лабораторная работа № 8. Численное дифференцирование и численное интегрирование функций
- •5. РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ И ПРОБЛЕМЫ СОБСТВЕННЫХ ЗНАЧЕНИЙ
- •5.1. Нормы векторов и матриц и их свойства
- •5.2. Обусловленность задачи решения системы линейных алгебраических уравнений
- •5.3. Метод Гаусса (схема единственного деления)
- •5.4. Метод прогонки
- •5.5. Метод простых итераций
- •5.6. Сходимость метода простых итераций
- •5.10. Постановка задачи нахождения собственных чисел
- •5.11. Подобные матрицы
- •5.12. Локализация собственных значений
- •5.13. Степенной метод
- •5.14. Вычисление собственных векторов методом обратных итераций
- •6. ЧИСЛЕННЫЕ МЕТОДЫ РЕШЕНИЯ НЕЛИНЕЙНЫХ УРАВНЕНИЙ И СИСТЕМ
- •6.1. Решение нелинейных уравнений
- •6.2. Метод Ньютона для уравнений
- •6.3. Сходимость метода Ньютона и трудности его применения
- •6.4. Метод Ньютона решения систем нелинейных уравнений
- •6.6. Модификации метода Ньютона
- •6.7. Лабораторная работа № 11. Решение систем нелинейных уравнений методом Ньютона
- •7. ЧИСЛЕННЫЕ МЕТОДЫ РЕШЕНИЯ ЗАДАЧИ КОШИ ДЛЯ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ И СИСТЕМ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
- •7.1. Задача Коши для дифференциального уравнения первого порядка
- •7.2. Численные методы решения задачи Коши. Основные понятия и определения
- •7.3. Решение с помощью рядов Тейлора
- •7.5. Анализ ошибок, возникающих при использовании методов Рунге - Кутты
- •7.6. Методы прогноза и коррекции
- •7.7. Сравнение методов
- •7.8. Лабораторная работа № 12. Методы интегрирования обыкновенных дифференциальных уравнений
- •7.9. Решение задачи Коши для систем обыкновенных дифференциальных уравнений
- •7.11. Лабораторная работа № 13. Численное интегрирование систем дифференциальных уравнений первого порядка
- •8. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ (УРАВНЕНИЯ МАТЕМАТИЧЕСКОЙ ФИЗИКИ)
- •8.1. Классификация уравнений математической физики
- •8.2. Простейшие задачи, приводящие к дифференциальным уравнениям в частных производных
- •8.4. Уравнения параболического типа. Явные и неявные схемы
- •Доказательство
- •8.5. Уравнения гиперболического типа
- •8.6. Уравнения эллиптического типа
- •8.7. Свойства разностных схем для дифференциальных уравнений: способность аппроксимировать исходную дифференциальную задачу, устойчивость и сходимость
- •8.8. Некоторые обобщения
- •8.9. Лабораторная работа № 14. Решение задачи Дирихле для уравнения Лапласа методом сеток
- •8.10. Лабораторная работа № 15. Решение однородного уравнения колебаний струны методом сеток по неявной схеме.
tg(xy)= x2 ,
0.7x2 + 2y2 =1.
cos y + x = 1.5,
23.2 y − sin(x − 0.5)=1.
|
|
|
|
2 |
|
|
25. |
tg(xy + 0.2)= x |
, |
||||
|
||||||
|
|
x2 + y2 |
=1. |
|
|
|
27. |
cos(x −1)+ y =1, |
|||||
|
|
= 1.6. |
||||
|
sin y + 2x |
|||||
cos x + y = 1.2,
29.2x − sin(y − 0.5)= 2.
22. |
cos(x + 0.5)+ y = 1, |
|||
|
sin y − 2x = 2. |
|||
|
|
|||
24. |
tg(x − y)− xy = 0, |
|||
|
x2 + 2 y2 =1. |
|||
|
|
|||
26. |
sin(x −1)+ y = 1.5, |
|||
|
x − sin(y +1)= 1. |
|||
|
|
|||
28. |
2x − cos(y +1)= 0, |
|||
|
y − sin x = −0.4. |
|||
|
|
|||
|
|
tg(xy)= x |
2 |
, |
30. |
|
|||
|
0.6x2 + 2y2 |
=1. |
||
|
|
|
|
|
7. ЧИСЛЕННЫЕ МЕТОДЫ РЕШЕНИЯ ЗАДАЧИ КОШИ ДЛЯ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ И СИСТЕМ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
7.1. Задача Коши для дифференциального уравнения первого порядка
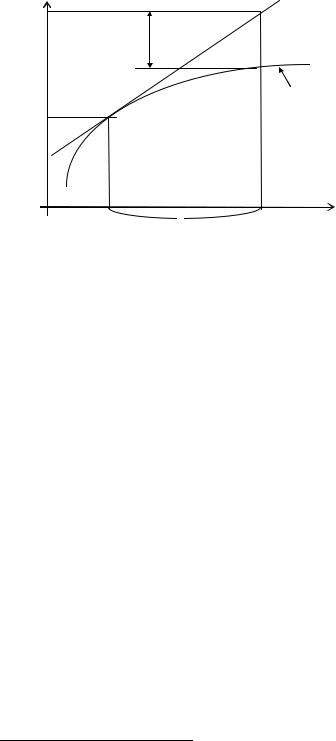
Большая часть инженерных задач приводит к законам и правилам, которые формулируются в виде дифференциальных уравнений. Основная задача, решаемая для таких уравнений, - это задача Коши или начальная задача. В подавляющем большинстве случаев она решается с использованием вычислительной техники. Рассмотрим методы решения дифференциальных уравнений первого порядка.
Решением |
обыкновенного дифференциального уравнения |
первого порядка |
|
y/ (x)= f (x, y(x)) |
называется функция y(x), обращающая это уравнение в тождество |
||
при подстановке. График решения называется интегральной кривой. |
|
||
f (x) |
|
f (x) |
|
|
|
α |
|
|
|
M (x0 , y0 ) |
|
k = tg α = f / (x, y) |
x |
x |
|
На рисунке справа изображено поле направлений, представляющее семейство инте- |
|||
гральных кривых уравнения |
y/ (x)= f (x, y(x)). |
|
|
|
|
(7.1.1) |
|
Задание начального условия - точки M (x0 , y0 ) выделяет из этого семейства конкретную кривую, дающую частное решение уравнения (7.1.1).
Задача нахождения при x > x0 решения |
y(x) дифференциального уравнения |
(7.1.1), удовлетворяющего начальному условию |
|
y(x0 )= y0 , |
(7.1.2) |
называется задачей Коши. Чаще всего решение ищут на конечном заданном отрезке [x0 , b].
162

Теорема 7.1. (Теорема существования и единственности решения). Пусть функция f (x, y) определена и непрерывна в области G и удовлетворяет в ней условию
Липшица по переменной y , то есть |
|
|
|
|
|
|
|
|
|
||
|
f (x, y1 )− f (x, y2 ) |
|
≤ c |
|
|
|
y1 − y2 |
|
, c = const. |
(7.1.3) |
|
|
|
|
|
||||||||
Тогда для любого начального значения y0 существует единственное решение |
y(x) за- |
||||||||||
дачи Коши с заданным начальным условием |
|
||||||||||
|
|
y/ = f (x, y(x)), |
|
||||||||
|
|
|
|
y(x0 )= y0 , |
|
||||||
определенное на отрезке [x0 , b] G. |
|
|
|
|
|
|
|
|
|
||
На практике для дифференцируемых по y функций f (x, y) условие (7.1.3) заменяет- |
|||||||||||
ся более грубым условием |
|
|
|
|
|
|
|
|
|
||
|
|
f y/ (x, y) |
|
≤ c, |
(7.1.4) |
||||||
|
|
|
|||||||||
то есть условием ограниченности частной производной.
7.2. Численные методы решения задачи Коши. Основные понятия и определения
Численное решение задачи Коши строится для ее дискретного аналога. В этом случае отрезок [x0 , X ] - область непрерывности изменения аргумента x заменяется множеством
ωh - конечным множеством точек x0 < x1 < ... < xN = X , которое называется сеткой. Величина hn = xn − xn−1 - шаг сетки - является, как правило, постоянным, то есть сетки в большинстве случаев равномерные.
Функции, определенные лишь в узлах сетки ωh , называются сеточными. Они поме-
чаются индексом h , например, f h , чаще же значение функции f (x) |
в узлах сетки |
|
h обо- |
|
ω |
||||
значается обычным образом с помощью индекса, например, f (xn ) или |
fn . |
|||
В основе построения конкретного численного метода лежит тот или иной способ за- |
||||
мены дифференциального уравнения y/ = f (x, y) его дискретным аналогом - уравнением |
||||
вида |
|
|
|
|
1 |
k |
|
|
|
∑a j yn+1− j = Φ(xn , yn+1−k ,..., yn , yn+1 , h), |
(7.2.1) |
|||
h |
j=0 |
|
|
|
где yh - значения сеточной функции в k +1 последовательных точках xn+1−k ,..., xn , xn+1. Сумма в левой части формулы (7.2.1) рассматривается как разностная аппроксимация производной y / по одной из формул численного дифференцирования, а правая часть - как специальным образом построенная аппроксимация функции f (x, y).
При нахождении приближения yn+1 в очередной точке сетки по формуле (7.2.1) используются найденные ранее значения сеточной функции yh в k предыдущих точках xn+1−k ,..., xn . Такие методы называются k -шаговыми. При k =1 уравнение (7.2.1) принимает вид
|
yn+1 − yn |
= Φ(xn , yn , yn+1 , h). |
(7.2.2) |
|
|
||
|
h |
|
|
Соответствующий этой формуле метод называется одношаговым. Вычисление yn+1 |
осущест- |
||
вляется здесь с использованием только одного предыдущего значения yn . |
|
||
Рудольф Липшиц (1832 - 1903) - немецкий математик.
163

В случае, когда входящая в уравнение (7.2.1) функция Φ не зависит от yn+1 , вычисление yn+1 не вызывает затруднений и осуществляется по явной формуле
yn+1 |
= a0−1 |
|
k |
|
|
− ∑a j yn+1− j + hΦ(xn , yn+1−k ,..., yn , h) . |
(7.2.3) |
||||
|
|
|
j=1 |
|
|
Соответствующие методы называются явными. Напротив, если Φ зависит от |
yn+1 , на каж- |
||||
дом шаге приходится решать относительно yn+1 нелинейное уравнение (7.2.1). Методы, реализующие такой алгоритм, называются неявными.
7.3. Решение с помощью рядов Тейлора
Начнем с метода, который теоретически пригоден для решения любых дифференциальных уравнений, но с вычислительной точки зрения не представляет почти никакого практического интереса. Его ценность заключается в том, что он дает некоторый эталон для сравнения различных практически удобных методов.
Запишем разложение функции y(x) в ряд Тейлора в окрестности точки xn+1 :
y(xn+1 )= y(xn + h)= yn + |
yn/ |
(xn+1 − xn )+ |
|
yn// |
(xn+1 |
− xn )2 + |
|
yn/// |
(xn+1 − xn )3 + ..., |
(7.3.1) |
|||
|
2! |
|
3! |
||||||||||
1! |
|
|
|
|
|
|
|
|
|
||||
где yn( j ) есть j -я производная функции y(x) |
в точке xn . Пусть имеется приближенное реше- |
||||||||||||
ние уравнения (7.3.1) для n +1 точки x0 , x1 ,..., xn , xi |
= x0 + ih, |
h = const. Найдем приближен- |
|||||||||||
ное решение для точки xn+1 , подставив xn+1 = xn |
+ h в формулу (7.3.1). Получим |
|
|||||||||||
/ |
+ |
h2 |
// |
|
h3 |
/// |
|
|
|
(7.3.2) |
|||
yn+1 = yn + hyn |
2 |
yn + |
6 |
yn +... |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
||
Чем больше членов ряда (7.3.2) взять для вычислений, тем точнее будет приближение. В лю- |
|||||||||||||
бом случае необходимо вычислять различные производные функции |
y(x). Из (7.1.1) имеем |
||||||||||||
yn/ = f (xn , yn ). Дифференцируя по x , получим |
|
|
|
|
|
|
|||||||
y// = |
∂ |
f (x, y)+ |
∂ |
f (x, y) y/ |
или yn// = fx/ |
+ f f y/ . |
(7.3.3) |
||||||
|
|
||||||||||||
|
∂x |
∂y |
|
|
|
|
|
|
|
|
|
||
При этом уравнение (7.3.2) приобретает вид |
|
|
|
|
|
|
|||||||
|
|
|
|
|
h |
/ |
/ |
|
|
3 |
|
|
|
|
yn+1 = yn + h f |
+ |
|
(fx + |
f f y |
) |
+ O(h |
|
). |
(7.3.4) |
|||
|
2 |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||
Процедура нахождения решения с помощью ряда Тейлора является одношаговым ме- |
|||||||||||||
тодом, так как для вычисления |
yn+1 |
требуется информация только об одной предыдущей |
|||||||||||
точке (xn , yn ). |
|
|
|
|
|
|
|
|
|
|
|
||
На практике очень трудно иногда найти |
fx/ и |
f y/ . Кроме того, если попытаться полу- |
|||||||||||
чить лучшее приближение, то есть меньшую ошибку, то необходимо вычислить yn/// , которая равна:
yn/// = fxx// + 2 f fxy// + f 2 f yy// + fx/ f y/ + f f y/ 2 . |
(7.3.5) |
Последующие производные становятся еще более сложными, а их вычисление чаще всего является весьма трудоемкой и даже невыполнимой операцией.
7.4. Методы Рунге - Кутты
Методы Рунге - Кутты обладают следующими отличительными свойствами:
Мартин Вильгельм Кутта (1867-1944) - немецкий физик и математик.
164
1) являются одношаговыми: чтобы найти yn+1 нужна информация только о предыдущей точке (xn , yn ) ;
2) согласуются с рядом Тейлора вплоть до членов порядка h p , где степень p различна для различных методов и называется порядком метода;
3) не требуют вычисления производных от f (x, y), а только вычисления функции.
Именно благодаря третьему свойству методы Рунге - Кутты более известны, нежели ряд Тейлора. Однако для вычисления одной последующей точки решения приходится вычислять f (x, y) несколько раз при различных значениях x и y.
|
Выведем сначала некоторые формулы на основе геометрических аналогий. |
|||||
|
yn+1 |
|
|
Пусть известна точка |
M (xn , yn ) |
|
|
|
|
|
на искомой кривой. Через |
эту точку |
|
|
ε |
L |
можно провести прямую с тангенсом уг- |
|||
|
|
|
|
ла наклона |
yn/ = f (xn , yn ). |
Тогда сле- |
|
|
|
y=f(x) |
дующей можно считать точку, где пря- |
||
yn |
M |
|
мая L пересечет ординату, проведенную |
|||
|
|
|||||
|
|
через точку |
x = xn+1 = xn + h. |
Уравнение |
||
|
|
|
|
|||
|
|
|
|
прямой L имеет вид y = yn + yn/ (x − xn ), |
||
|
L : y = yn + yn/ |
(x − xn ) |
но так как |
yn/ = f (xn , yn ) и xn+1 = xn + h , |
||
|
|
|
|
то yn+1 = yn |
+ hf (xn , yn ). |
(7.4.1) |
|
xn |
h |
xn+1 |
Формула (7.4.1) описывает метод Эйле- |
||
|
ра , один из самых старых и широко из- |
|||||
вестных методов численного интегрирования дифференциальных уравнений. Формула (7.4.1) может быть получена из (7.2.2), если принять Φ(xn , yn , yn+1 , h)≡ f (xn , yy .). Так как здесь функция Φ не зависит от yn+1 , то метод является явным.
Ошибка интегрирования при x = xn+1 показана на рисунке в виде отрезка ε. Очевидно, что найденное таким образом приближенное решение согласуется с разложением в ряд
Тейлора вплоть до членов порядка h , так что ошибка равна ε = Kh 2 . |
|
|
|
|
|
|
||||||||||||
|
|
Теорема 7.2. |
Пусть функция f (x, y) |
удовлетворяет условию |
|
f y/ |
|
≤ M . |
Тогда |
|||||||||
|
|
|
||||||||||||||||
справедливо неравенство |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
N −1 |
|
|
|
|
|
|
|
|
|
|
|
max |
|
|
|
+ h∑ |
ψk |
|
|
|
|
|
(7.4.2) |
||||
|
|
|
yn − yn |
≤ exp(M (X − x0 )) |
|
y0 − y0 |
, |
|
|
|
|
|
||||||
|
|
|
0≤n≤N |
|
|
|
|
|
k =0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
то |
есть |
метод |
Эйлера |
устойчив |
|
|
на |
конечном |
отрезке. |
Здесь |
||||||||
ψn = |
1 |
∑k a j y(xn+1− j )− Φ(xn , y(xn+1−k ),..., y(xn+1 ), h) |
- |
погрешность аппроксимации дискрет- |
||||||||||||||
|
||||||||||||||||||
|
h j=0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ного уравнения (7.2.1) на решении y(x).
Метод Эйлера, реализуемый формулой (7.4.1), можно усовершенствовать множеством различных способов. Рассмотрим две модификации: а) исправленный метод Эйлера и б) модифицированный метод Эйлера.
а). В исправленном методе Эйлера находим средний тангенс угла наклона касательной для двух точек (xn , yn ) и (xn + h, yn + hyn/ ). Геометрически процесс нахождения точки
(xn+1 , yn+1 ) можно проследить по левому рисунку на следующей странице. С помощью метода Эйлера находится точка (xn + h, yn + hyn/ ), лежащая на прямой L . В этой точке снова вы-
Леонард Эйлер (1707-1783) - швейцарский математик. Долгое время жил и работал в России.
165
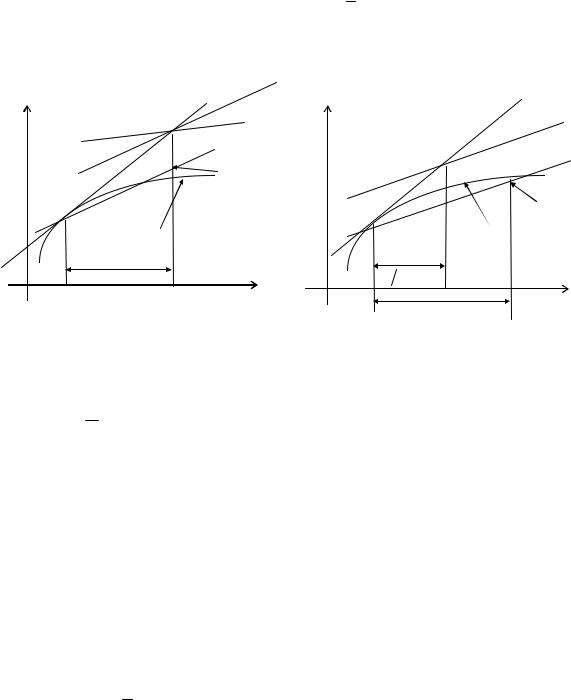
числяется тангенс угла наклона касательной, на рисунке этому значению соответствует прямая L1 . Усреднение двух тангенсов дает прямую L . Наконец, через точку (xn , yn ) проводим
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
прямую L1 , параллельную |
|
L |
. Точка, в которой прямая |
|
L1 пересечется с ординатой |
xn+1 и |
|||||||||||||||
будет искомой точкой (xn+1 , yn+1 ). |
|
|
|
|
|
|
|
|
|
|
|||||||||||
а) |
|
|
L |
|
|
|
|
L1 |
б) |
|
|
|
L |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
(x |
|
|
|
|
|
) |
|
|
|
L |
|
|
|
|
|
|
|
|
|
|
|
, y |
|
|
|
|
|
|
L |
|
|||
|
|
L |
L |
|
|
n+1 |
n+1 |
|
|
|
|
||||||||||
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
1 |
|
|||||
M (xn , yn ) |
y = f (x) |
|
|
|
|
|
|
|
|
M (xn , yn ) |
|
|
|
(xn+1 , yn+1 ) |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y = f (x) |
|
|||
|
|
|
|
|
h |
|
|
|
|
|
|
|
|
h 2 |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
xn |
|
|
xn+1 |
|
|
|
|
|
|
|
|
xn |
|
|
h |
xn+1 |
|
||||
Тангенс угла наклона прямой |
|
равен: |
|
|
|
|
|
||||||||||||||
L |
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
Φ(xn , yn , h)= |
1 |
[f (xn , yn )+ f (xn + h, yn + hyn/ |
)], yn/ |
= f (xn , yn ). |
(7.4.3) |
|||||||||||
|
|
|
|
|
2 |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Уравнение L1 при этом записывается в виде y = yn + (x − xn )Φ(xn , yn , h). Таким образом,
yn+1 |
= yn + hΦ(xn , yn , h)= yn + |
h |
[f (xn , yn )+ f (xn + h, yn + hyn/ )]. . |
(7.4.4) |
|
||||
|
2 |
|
|
|
Это и есть рабочее уравнение исправленного метода Эйлера.
Выясним, как хорошо этот метод согласуется с разложением в ряд Тейлора. Для этого
запишем разложение в ряд Тейлора для функции |
двух переменных |
в |
окрестности |
||||||
точки M (xn , yn ): |
f (x, y)= f (xn , yn )+ (x − xn ) |
∂f (xn , yn ) |
|
+ (y − yn ) |
∂f (xn , yn ) |
|
+... |
Если поло- |
|
∂x |
∂y |
||||||||
|
|
|
|
|
|||||
жить здесь x = xn |
+ h и y = yn + hyn/ , yn/ = f (xn , yn ), то получим |
|
|
||||||
f (xn + h, yn + hyn/ )= f + hfx/ + hf f y/ + O(h2 ).
Подставляя этот результат в (7.4.3) и производя необходимые преобразования, будем иметь Φ(xn , yn , h)= f + h2 (fx/ + f f y/ )+ O(h2 ), что совпадает с (7.3.2) вплоть до членов степени h2.
Такимобразом, исправленныйметодЭйлераявляетсяметодомРунгеКутты второго порядка. б). Если в рассмотренном методе усреднялись наклоны касательных, то в модифици-
рованном методе |
Эйлера усредняются точки (смотрите рисунок справа). Первоначальное |
построение сделано точно так же, как и в предыдущем случае - через точку M (xn , yn ) про- |
|
ведена прямая L |
с тангенсом угла наклона, равным f (xn , yn ). Затем взята точка на |
пересечении этой прямой и ординаты
точке
Φ(xn , yn , h) =
x = xn + |
h |
. |
Угол наклона касательной L |
в этой |
||||||
|
||||||||||
|
|
|
2 |
|
|
|
|
|
||
|
|
h |
|
|
|
|
h |
/ |
|
|
f xn |
+ |
|
, yn |
+ |
|
yn . |
(7.4.5) |
|||
2 |
2 |
|||||||||
|
|
|
|
|
|
|
|
|||
166

Проведем через точку M (xn , yn ) прямую L1 , параллельную L . Пересечение этой прямой с ординатой x = xn + h и даст искомую точку (xn+1 , yn+1 ). Так как уравнение прямой L1 можно записать в виде y = yn + (x − xn )Φ(xn , yn , h), то
|
|
h |
|
h |
/ |
|
|
yn+1 |
= yn + hΦ(xn , yn , h)= yn + hf xn + |
|
, yn + |
|
yn . |
(7.4.6) |
|
2 |
2 |
||||||
|
|
|
|
|
Формула (7.4.6) описывает модифицированный метод Эйлера.
Влитературе исправленный метод Эйлера называют иногда методом Эйлера - Коши ,
амодифицированный метод - усовершенствованным. Как и в предыдущем случае, можно легко показать, что модифицированный метод является методом Рунге - Кутты второго по-
рядка.
Оба рассмотренных метода описываются формулами вида yn+1 = yn + hΦ(xn , yn , h),
причем в обоих случаях функция Φ имеет вид
Φ(x |
n |
, y |
n |
, h)= a |
f (x |
n |
, y |
n |
)+ a |
2 |
f (x |
n |
+ b h, y |
n |
+ b hy / |
), |
y / |
= f (x |
n |
, y |
n |
). |
|
|
|
|
(7.4.7) |
||
|
|
1 |
|
|
|
|
1 |
|
2 n |
|
n |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
= a2 |
1 |
|
|
|
|
|
|
|
|
|
a |
= 0, |
a |
|
=1, |
|||
Для исправленного метода Эйлера a1 |
|
= 2 , |
а для модифицированного |
1 |
|
|
2 |
1 |
. |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
= b2 |
= 1, |
|
|
|
|
|
|
|
|
|
b1 = b2 |
= |
2 |
|||||
|
|
|
|
|
|
|
|
|
b1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Методы Рунге - Кутты третьего и четвертого порядков можно вывести совершенно
аналогично тому, как это делалось при выводе методов первого и второго порядков. Общая идея вывода формулы метода Рунге - Кутты любого заданного порядка состоит в следующем.
Пусть y(x) |
- решение дифференциального уравнения y/ (x)= f (x, y(x)), |
удовлетво- |
|
ряющее условию y(xn )= yn . Проинтегрируем уравнение y/ |
= f (x, y) по x от xn |
до xn+1 , по- |
|
xn+1 |
xn+1 |
|
|
лучим ∫ y / (x)dx = |
∫ f (x, y(x))dx. По формуле Ньютона - Лейбница |
|
|
xn |
xn |
|
|
xn+1 |
xn+1 |
|
|
∫ y/ (x)dx = y(xn+1 )− y(xn ). Тогда yn+1 = yn + ∫ f (x, y |
(x))dx. |
(7.4.8) |
|
xn |
xn |
|
|
Если бы интеграл в формуле (7.4.8) вычислялся точно, то она была бы основной рабочей формулой всех методов численного интегрирования дифференциальных уравнений. В дейст-
вительности используют приближенную формулу, заменяя интеграл квадратурной суммой. |
|||||||||||||||||||||
Введем на |
отрезке |
|
[x |
n |
, x |
n+1 |
] |
m |
|
вспомогательных |
узлов x(1) = x |
n |
+ a h , |
||||||||
x(2) = x |
|
|
|
x(m ) = x |
|
|
|
|
|
|
|
|
|
|
|
|
n |
1 |
|||
n |
+ a |
h ,..., |
n |
+ a |
m |
h , где 0 = a |
≤ a |
2 |
≤ ... ≤ a |
m |
≤1. Тогда интеграл в уравнении |
||||||||||
n |
2 |
|
n |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|||||
(7.4.8) можно заменить квадратурной суммой с узлами xn(1), xn(2),..., xn(m), |
то есть |
|
|
||||||||||||||||||
|
|
|
|
y(xn+1 )≈ y(xn )+ h∑m |
ci f (xn(i ), y(xn(i ))). |
|
(7.4.9) |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
i=1 |
|
|
|
|
|
|
|
|
Здесь неизвестны значения y(xn(i ) ). Применяя формулу (7.4.8), получим
xn(i )
y(xn(i ))= y(xn )+ ∫ f (x, y(x))dx, i = 2,3,..., m.
xn
Огюст Луи Коши (1789-1857.) - французский математик.
Готфрид Вильгельм Лейбниц (1646 - 1716.) - немецкий математик, создатель дифференциального исчисления.
167
Заменим для каждого i |
входящий в эту формулу интеграл соответствующей ему квадратур- |
|||||||||||||||
ной суммой с узлами xn(1), xn(2),..., xn(m ) : |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
y(xn(2))≈ y(xn )+ hb21 f (xn(1), y(xn(1))), |
y(x(2)))), |
||||||||||||
y(x(3)) |
≈ y(x |
n |
)+ h(b f (x(1), y(x(1)))+ b f (x |
(2), |
||||||||||||
|
n |
|
|
|
31 |
n |
|
|
n |
|
32 |
n |
n |
|||
................................................................................... |
||||||||||||||||
|
|
|
|
|
|
|
|
|
i−1 |
|
|
|
|
|
|
|
|
|
|
y(xn(i ))≈ y(xn )+ h∑bij f (xn(j ), y(xn( j ))), |
(7.4.10) |
||||||||||||
|
|
|
|
|
|
|
|
|
j=1 |
|
|
|
|
|
|
|
|
|
|
........................................................... |
|
||||||||||||
|
|
|
|
|
|
|
|
|
m−1 |
|
|
|
|
|
|
|
|
|
y(xn(m))≈ y(xn )+ h∑bmj f (xn(j ), y(xn(j ))). |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
j=1 |
|
|
|
|
|
|
|
Формулы (7.4.10) позволяют последовательно вычислять приближения к значениям |
||||||||||||||||
y(xn(2)), y(xn(3)),..., y(xn(m )). Пусть |
yn(i ) = y(xn(i )), kn(i ) |
= f (xn(i ), yn(i )). |
Тогда формулу (7.4.8) можно |
|||||||||||||
переписать в виде |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m |
|
|
|
|
|
|
|
yn+1 = yn + hkn , kn = ∑ci kn(i ), |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
i=1 |
|
|
|
|
|
|
|
|
|
kn(1) = f (xn(1), yn(1) ), yn(1) |
= yn , |
|
|
||||||||
|
|
kn(2) |
= f (xn(2), yn(2) ), |
yn(2) = yn |
+ hb21kn(1), |
(7.4.11) |
||||||||||
|
|
|||||||||||||||
|
.......................................................... |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
kn(m) = f (xn(m), yn(m)), yn(m) = yn + hm∑−1bmj kn(j ). |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
j=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Если исключить отсюда величины yn(i ) , получим |
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
m |
|
|
|
|
|
|
|
|
yn+1 = yn + hkn , kn = ∑ci kn(i ), |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
i=1 |
|
|
|
|
|
|
|
|
|
|
kn(1) = f (xn , yn ), |
|
(1)), |
|
|
||||||
|
|
|
k |
(2) |
= f (x |
n |
+ a |
h, y |
n |
+ hb k |
|
(7.4.12) |
||||
|
|
|
|
n |
|
|
2 |
|
|
|
21 |
n |
|
|
||
|
|
................................................... |
|
|
||||||||||||
|
|
|
(m) |
|
|
|
|
|
|
|
|
m−1 |
( j ) |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
kn |
= |
|
|
|
|
|
|
|
|
|||||
|
|
f xn + amh, yn + h∑bmj kn . |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
j=1 |
|
|
||
Выбор конкретных значений параметров |
ci , ai |
и bi осуществляется по-разному и да- |
||||||||||||||
ет ту или иную модификацию методов Рунге - Кутты. Приведем рабочие формулы метода четвертого порядка. Он применяется настолько широко, что в литературе называется просто «методом Рунге - Кутты» без всяких указаний на тип или порядок. Этот классический метод Рунге - Кутты описывается системой следующих шести уравнений:
y |
n+1 |
= y |
n |
+ hk |
n |
, |
k |
n |
= |
1 (k |
(1) + |
2k (2) + 2k (3) + k (4)), |
||||||||||
|
|
|
|
|
|
|
6 |
|
n |
|
|
|
|
|
n |
|
n |
n |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
), |
|
|
|
||
|
|
|
|
|
|
k |
(1) = f (x |
n |
, |
y |
n |
|
|
|
||||||||
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
k (2) |
= |
f |
x |
n |
+ h , y |
n |
+ h k (1) , |
(7.4.13) |
||||||||||
|
|
|
|
n |
|
|
|
|
|
|
2 |
|
|
|
|
|
2 |
n |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
h |
|
|
|
|
|
|
h |
(2) |
|
||
|
|
|
|
(3) |
= |
f |
|
|
+ |
, yn |
+ |
|
||||||||||
|
|
|
|
kn |
xn |
2 |
2 |
kn |
, |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
(4) |
|
|
|
|
|
|
|
|
|
|
|
(3) |
|
|||||
|
|
|
|
kn |
|
= f |
(xn + h, yn + hkn |
). |
|
|||||||||||||
Ошибка метода ε = Kh5 , |
при его использовании функцию необходимо вычислять дважды. |
|||||||||||||||||||||
168
