Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Балтийский государственный технический университет "ВОЕНМЕХ" им. Д.Ф. Устинова

Предмет:

Вычислительная математика

Файл:

шапорев выч мат.pdf

Скачиваний:

766

Добавлен:

26.03.2015

Размер:

8.33 Mб

Скачать

☆

<<< < Предыдущая 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 3031 / 3631 32 33 34 35 36 > Следующая >>>

	y /		= ln(x					+ y								2 + y										2 ),									y			(1)= 0,
		1													1											3					x [1, 4],						1
23.	y2/			= sh(xy1 y2 )+ y3 ,																											x [1, 4],				y2				(1)=1,
	y /			= y + 3y											2			− xy2											,				y			3		(1)= −1.
		3			1										2											3										3
	y /			= xy			+ x2										y			2		y			3	,						y				(0)					= −0.3,
		1			1															2					3						x [0, 3],			1				(0)= 0.5,
24.	y2/		= −y1 − y2															+ y32 ,													x [0, 3],		y2					(0)= 0.5,
				/	= xe				−(y +y										2		)		,												y3 (0)=1.
			y3		= xe								1						2				,												y3 (0)=1.
		y		/	= arctg(xy y																			3		),												y		(1)= 0,
			1																1					3							x [1, 4],								1
25.	y2/		= sin(arctg(y1 y3 )),																												x [1, 4],			y2 (1)= −0.3,
				/	= e	−(y							+y				2		+y				3		)	,												y3 (1)=1.
			y3		= e						1						2						3			,												y3 (1)=1.
	y /		= x(y						+ y							2		sin y										3		),								y			(1)= 0,
		1			1											2												3			x [1, 3],									1
26.		y2/		= x cos(y2															+ y3 ),												x [1, 3],				y2				(1)= −0.5,
			y /		= ln(x2											+ y2 ),																					y		3	(1)= 0.5.
				3																			1																3
	y /				= y y						2		y			3		,														y		(0)= 0,
				1	1						2					3												x [0, 4],				1
27.		y2/			= x2 + y12 ,																),							x [0, 4],				y2 (0)= −0.5,
	y3		= ln(x				2				+ y2										),											y3 (0)= 0.5.
		/					2											2
		y	/	= 2 y						+ y							2		y			3		,								y			(0)= 0.2,
		1				1											2					3								x [0, 4],			1				(0)= 0,
28.	y2/			= y1 y2 y3												+ y12 ,														x [0, 4],		y2					(0)= 0,
	y /		= xy + y											2			− y							2		,							y		3		(0)= 0.
		3			1									2										3											3
	y /				= ln(x2 + y																		2 ),																y			(−1)= 0,
				1																		1									x [−1, 3],									1
29.		y2/			= arctg(xy1 y3 ),																										x [−1, 3],							y2			(−1)= −1,
	y /		= sin(arctg(y y																							3		)),											y		3	(−1)=1.
		3																			1					3															3
	y /			= sin y								cos3													y		2		,									y		(−1)= 0,
		1							1																		2				x [−1, 3],								1		(−1)= 0,
30.	y2/			= x cos y1 cos y3 ,																											x [−1, 3],							y2			(−1)= 0,
		/	= sin(x − y2																	− y3 ),																		y3 (−1)= 0.
	y3		= sin(x − y2																	− y3 ),																		y3 (−1)= 0.

8. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ (УРАВНЕНИЯ МАТЕМАТИЧЕСКОЙ ФИЗИКИ)

8.1. Классификация уравнений математической физики

Дифференциальным уравнением с частными производными называется уравнение относительно неизвестной функции u(x, y) двух или более независимых переменных, кото-

рое содержит частные производные этой функции.

Порядком дифференциального уравнения называется наибольший порядок производных, входящих в это уравнение.

Важнейшее значение с точки зрения приложений в физике и технике имеют уравнения с частными производными второго порядка, поэтому основное внимание будет уделено изучению именно таких уравнений. В общем виде дифференциальное уравнение второго порядка относительно функции двух независимых переменных u(x, y) записывается следую-

щим образом:

∂u

, ∂

∂

F x, y,u,

= 0 ,

(8.1.1)

∂x

∂y ∂x

∂y

∂x∂y

где F - заданная функция восьми аргументов.

188

Далее будут рассматриваться, в основном, уравнения более простого вида, чем (8.1.1), а именно, линейные уравнения второго порядка

a(x, y)	∂2u	+ 2b(x, y)	∂2u	+ c(x, y)	∂2u	+ d(x, y)∂u	+ e(x, y)∂u	+ g(x, y)u = f (x, y),	(8.1.2)
	∂x2		∂x∂y		∂y2
						∂x	∂y

где коэффициенты a(x, y), b(x, y),..., g(x, y) и правая часть f (x, y) - функции, не зависящие

от u , которые заданы и непрерывны в некоторой области D , называемой областью определения дифференциального уравнения.

Если все коэффициенты уравнения (8.1.2) не зависят от x и y , то оно называется уравнением с постоянными коэффициентами, если же f (x, y)= 0 , уравнение называется од-

нородным.

Естественно возникает вопрос о существовании наиболее компактной формы записи уравнения (8.1.2). Оказывается, этого можно добиться надлежащей заменой переменных.

Перепишем уравнение (8.1.2) в следующем виде:

a u //

+ 2a u

+ a

u // + F (x, y, u(x, y),u / ,u / )= 0 ,

(8.1.3)

где a11 = a11 (x, y),

a12 = a12 (x, y),

a22 = a22 (x, y),

f (x, y)= 0 . Это уравнение называется линей-

ным относительно старших производных.

Сделаем в нем замену переменных ϕ = ϕ(x, y)

ψ = ψ(x, y), обеспечивающую взаимно однозначное соответствие между x, y и ϕ, ψ . Тогда

ϕ = ϕ(x, y),

x = x(ϕ, ψ),

ϕ/x

ψ/x

≠ 0 .

Так

как

u = u(x, y),

то

= y(ϕ, ψ)

ϕ/y

ψ/y

ψ = ψ(x, y),

/ = [u(ϕ(x, y), ψ(x, y))]/

∂u

∂ϕ

∂u

∂ψ

u /

∂u

∂ϕ

∂u

∂ψ

Найдем

вторую произ-

∂ϕ ∂x

∂ψ ∂x

∂ϕ ∂y

∂ψ ∂y

водную по x , расписав подробно получающееся выражение:

∂u

∂ϕ

∂u

∂ψ /

∂u

∂ϕ /

∂u

∂ψ

∂u

u //

∂ϕ ∂x

∂ψ

∂x

∂ϕ

∂ψ

∂x

∂ϕ

∂x x

∂u

∂u(ϕ(x, y), ψ(x, y)) /

∂u

∂ψ

∂u

∂2

∂ϕ x

∂ϕ

∂x

∂ψ ∂x2

∂2u

∂ϕ

∂2u

∂ψ

∂ψ x

∂ϕ2

∂x +

∂ϕ∂ψ

∂x

∂∂ϕx + ∂ϕ∂u ∂∂x2 ϕ2 +

=∂2u ∂ϕ +∂ϕ2 ∂x

∂2u

∂ψ

∂ϕ

∂u

∂2 ϕ

∂2u

∂ϕ

∂2u

∂ψ

∂u

∂2

∂ϕ∂ψ

∂x

∂ϕ

∂x2

∂ϕ∂ψ ∂x

∂ψ2

∂x

∂ψ

∂x2

∂x

∂2u

∂ϕ 2

∂2u

∂ϕ

∂ψ

∂u

∂2

∂2u

∂ϕ

∂ψ

∂2u

∂ψ

∂x

∂x2

∂x

∂ϕ2

∂ϕ∂ψ

∂ϕ

∂ϕ∂ψ

∂ψ2

∂x

∂u

∂2 ψ

∂2u

∂ϕ

∂2u

∂ψ 2

∂2u

∂ϕ

∂ψ

∂u

∂2

∂u

∂2 ψ

∂x2

∂x

+ 2

∂x

∂x2

∂x

∂ψ

∂ϕ2

∂ψ2

∂ϕ∂ψ

∂ϕ

∂ψ

∂x

= uϕϕ// (ϕ/x )2 + uψψ// (ψ/x )2 + 2uϕψ// ϕ/x ψ/x + uϕ/ ϕ//xx + uψ/ ψ//xx .

Аналогично можно записать и uyy// = uϕϕ// (ϕ/y )2 + uψψ// (ψ/y )2 + 2uϕψ// ϕ/y ψ/y + uϕ/ ϕ//yy + uψ/ ψ//yy ,

uxy// = uϕϕ// ϕ/x ϕ/y + uψψ// ψ/x ψ/y + uϕψ// (ϕ/x ψ/y + ϕ/y ψ/x )+ uϕ/ ϕ//xy + uψ/ ψ//xy . Подставляя эти значения в

уравнение (8.1.3), получим

a11 (uϕϕ// (ϕ/x )2 + uψψ// (ψ/x )2 + 2uϕψ// ϕ/x ψ/x + uϕ/ ϕ//xx + uψ/ ψ//xx )+ 2a12 (uϕϕ// ϕ/x ϕ/y +uψψ// ψ/x ψ/y + uϕψ// (ϕ/x ψ/y +
+ ϕ/y ψ/x )+ uϕ/ ϕ//xy + uψ/ ψ//xy )+ a22 (uϕϕ// (ϕ/y )2 + uψψ//					(ψ/y )2 + 2uϕψ// ϕ/y ψ/y + uϕ/ ϕ//yy + uψ/ ψ//yy				)+
+ F	(ϕ, ψ,u(ϕ, ψ),u /	ϕ/	+ u /	ψ/ ,u /		ϕ/	+ u /	ψ/ )= 0
1	ϕ	x	ψ	x	ϕ	y	ψ	y

189

или

~ //

где

a11uϕϕ + 2a12uϕψ + a22uψψ + F = 0,

= F1 (ϕ, ψ,u,uϕ

,uψ ),

a11

= a11 (ϕx )

+ 2a12 ϕx

ϕy

+ a22 (ϕy

) ,

ψy ,

a12

= a11ϕx ψx + a12 (ϕx ψx + ϕy ψy )+ a22

ϕy

/ /

+ 2a12

a22

= a11 (ψx )

ψx ψy + a22 (ψy

) .

Естественно, для упрощения уравнения

= 0 в новых пе-

a11uϕϕ + 2a12uϕψ + a22uψψ + F

ременных ϕ и ψ надо так подобрать эти переменные, чтобы хотя бы некоторые члены рассматриваемого уравнения упрощались или вообще обнулялись. Например, можно выбрать ϕ

так,

чтобы

Для

этого

рассмотрим

вспомогательное

уравнение

a11 = 0 .

z / 2

+ 2a

z /

+ a

/ 2 = 0 , где

z = z(x, y). Пусть ϕ(x, y) - какое-нибудь частное решение

если ψ(x, y)

этого уравнения. Если теперь выбрать

= 0 . Аналогично,

- другое

z = ϕ , то a11

частное решение этого же уравнения и

= 0 .

z = ψ , то a22

Теорема

8.1.

Если

z = ϕ(x, y)

является

частным

решением

уравнения

z / 2

+ 2a

z /

+ a

/ 2 = 0 , то ϕ(x, y)= C есть общий интеграл обыкновенного диффе-

ренциального уравнения

dy2 − 2a

dxdy + a

dx2 = 0 .

(8.1.4)

Наоборот, если ϕ(x, y)= C

общий интеграл обыкновенного дифференциаль-

ного

уравнения

(8.1.4),

то

функция

z = ϕ(x, y)

удовлетворяет

уравнению

a z/ 2

+ 2a z/

z/ + a

z/ 2 = 0 .

Решим

уравнение

(8.1.4),

преобразовав

его:

− 2a

+ a

= 0 ,

11 dx

2a12

± 4a122 − 4a11a22

a12 ± a122 − a11a22

Таким образом, получим два обыкно-

2a11

a11

dx 1,2

венных дифференциальных уравнения:

a12 +

a122

− a22

a11

(8.1.5)

a12 −

a122

− a22

Знак подкоренного выражения определяет тип исходного уравнения (8.1.3) в частных

производных.

M (x, y)

− a

1. Если в точке

> 0 , то уравнение a

u //

+ 2a

u //

+ a

u //

+ F = 0 в

этой точке называется уравнением гиперболического типа.

2. Если в точке M (x, y) a122 − a11a22 < 0 , то уравнение a11uxx// + 2a12 uxy// + a22 u yy// + F = 0 в этой точке называется уравнением эллиптического типа.

3. Если в точке M (x, y) a122 − a11a22 = 0 , то уравнение a11uxx// + 2a12 uxy// + a22 u yy// + F = 0 в этой точке называется уравнением параболического типа.

	Так	как	~ 2	~ ~		2	− a11a22 )D , то сказанное справедливо и для уравнения
~ //			a12	− a11a22		= (a12
	~	//	~	//	~	= 0 .
a11uϕϕ + 2a12uϕψ			+ a22uψψ		+ F

Уравнение (8.1.4) называется характеристическим для уравнения (8.1.3), а интегралы уравнения (8.1.4) - характеристиками уравнения (8.1.3). Пусть в заданной области G уравнение (8.1.3) однотипно. Рассмотрим все три возможные случая подробнее.

190

1. Гиперболический тип.

Два

общих

интеграла

уравнения

(8.1.3)

ϕ(x, y)= C

ψ(x, y)= C

определяют

действительные семейства

характеристик.

Пусть

ϕ = ϕ(x, y)

ψ = ψ(x, y)

новые

переменные

уравнении

(8.1.3).

Тогда

= 0

или

2a12uϕψ

+ F

uϕψ

= −(F

2a12 ) - первая каноническая форма уравнения гиперболического типа. Если по-

ϕ = α +β,

ϕ+ ψ

ложить

α =

то uϕ/

= u(α +β, α −β)ϕ/

= uα/ αϕ/ + uβ/ βϕ/

= uα/

+ uβ/

ψ = α −β,

ϕ−ψ

β =

(uα/

+ uβ/ ).

Аналогично, uψ/

(uα/

− uβ/ )

uϕψ//

(uαα// − uββ// ).

результате

исходное

= F1 . Это вторая каноническая форма уравнения

уравнение примет вид uαα −uββ = −(2F a12 )

гиперболического типа.

− a a

2. Параболический тип. Для уравнения этого типа

= 0 , имеется, следова-

тельно,

лишь

один

общий

интеграл

характеристического

уравнения

a dy2

− 2a

dxdy + a

dx2

= 0 .

Пусть

этот

интеграл

ϕ(x, y)

= C ,

положим

ϕ = ϕ(x, y),

ψ = ψ(x, y)

где

любая

функция,

не

зависящая

от

ϕ .

Тогда

(

= 0

a11

= a11 (ϕx )

+ 2a12 ϕx

ϕy

+ a22 (ϕy

) =

a11 ϕx

a22 ϕy ) = 0 , потому что при a12 − a11a22

a12

a11a22

/ /

= (

)×

a12 = a11ϕx ψx + a12 (ϕx ψy

+ ϕy

ψx )+ a22 ϕy

ψy

a11 ϕx

a22 ϕy

× (

a11 ψ/x +

a22 ψ/y )= 0 .

Тогда

исходное

для

этого

случая

уравнение

a11uϕϕ

+ 2a12uϕψ + a22uψψ + F = 0

обратится в следующее:

uψψ

= −(F a22 ) = Φ(ϕ, ψ,u,uϕ ,uψ ).

~ ~

Это канонический вид уравнения параболического типа.

a12

a122 − a22

a11

3. Эллиптический тип. Для этого типа уравнения

имеют ком-

a12

−

a122 − a22

плексные общие интегралы. По свойству комплексной переменной, если ϕ(x, y)= C - реше-

ние уравнения

a dy2

− 2a dxdy + a

dx2

= 0 , то ϕ (x, y)

- комплексно-сопряженная функция

ψ = ϕ (x, y), тогда уравнение эл-

также будет решением этого уравнения. Пусть ϕ = ϕ(x, y),

липтического типа сведется к тому же виду, что и гиперболическое. Чтобы не иметь дело с

комплексными

переменными,

введем новые

переменные

α =

ϕ+ ψ

, β =

ϕ− ψ

, тогда

ϕ = α + iβ, ψ = α −iβ . При этом предполагается, что a11, a12 , a22

- аналитические функции.

Вычислим a

(ϕ/

)2 + 2a

ϕ/

ϕ/ + a

(ϕ/ )2

= 0 = a (ϕ/

α/

+ ϕ/

β/

)2 + 2a

(ϕ/

α/ +

+ ϕβ/ β/x )(ϕα/

α/y + ϕβ/ β/y )+ a22 (ϕα/ α/y

+ ϕβ/ β/y )2 = a11 (1 α/x + i β

/x )2 + 2a12 (α/x + i β/x )

(α/y + i β/y )

+ a22 (α/y + i β/y )2 = a11

(α/x 2 + 2iα/xβ/x − β/x 2

)+ 2a12

(α/x α/y + iα/yβ/x + iα/xβ/y −

− β/xβ/y )+ a22

(α/y 2 + 2iα/yβ/y

− β

/y 2

)= (a 1α/x 2 + 2a12 α/x α/y + a22 α/y 2 )−

1444442444443

− (a 1β/x 2 + 2a12β

/y 2 )+ 2i(a

1α/xβ/x + a12 (α

a11

/y )

+ α/yβ/y )

/xβ/y + a22β

/yβ

/x + α/xβ

= 0

1444442444443

14444444244444443

a22

a12

191

Отсюда

по

свойству комплексных

чисел

следует,

что

= 0,

a12

a11

= a22 , так как

= 0

превратится

в следующее

a11

− a22 = 0 . Тогда уравнение

a11uϕϕ + 2a12uϕψ + a22uψψ

+ F

уравнение: a11uαα + a22uββ

= −F

или

uαα + uββ

= −

= Φ(α,β,u,uα ,uβ ) -

канонический вид

уравнения эллиптического типа.

a11

Итак: 1)

− a

> 0 - гиперболический тип и u //

− u //

= Φ

или u //

= Φ - канони-

ческий вид уравнения;

2)a122 − a11a22 < 0 - эллиптический тип, а uxx// + uyy// = Φ - канонический вид уравнения;

3)a122 − a11a22 = 0 - параболический тип и uxx// = Φ - канонический вид уравнения.

Пример. Найти области гиперболичности, эллиптичности и параболичности уравне-

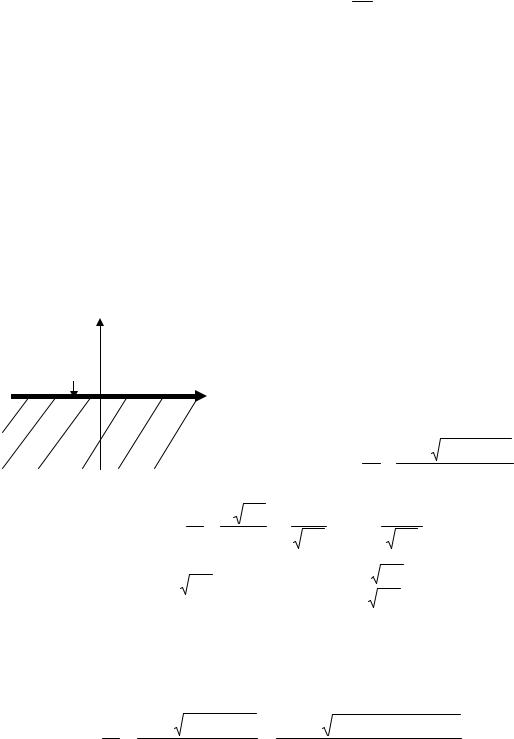
ния uxx//

+ yu yy// = 0 и привести его к каноническому виду в области гиперболичности.

Дифференциальное уравнение в частных производных, содержащее явно все необхо-

димые

коэффициенты,

имеет

вид

+ 2a

+ a

+ F = 0 . В

нашем

случае

=1,

= 0,

= y

то есть

− a

= 0 −1 y = −y . Тип уравнения зависит от знака

выражения

− a

. Если оно отрицательно, то это эллиптический тип,

положительно -

гиперболический, равно нулю – параболический:

− y > 0,

y < 0 -

область гиперболического типа;

− y < 0,

y > 0 -

область эллиптического типа;

эллиптический

у = 0 - область параболического типа.

параболический

Все области изображены на рисунке слева. Приведем

теперь исходное уравнение к каноническому виду. Для

этого решим уравнения (8.1.5):

a12 ±

a122

−a11a22

гиперболический

a11

= ± − y

, ±

= dx,

m d(− y)

= dx,

− y

m 2 − y = x + C . Итак,

− y − x,

uϕψ//

ϕ = −2

= 0.

ψ = 2

− y − x.

Пример. Привести к каноническому виду следующее дифференциальное уравнение

∂2u

+ 2 sin x

∂2u

− cos

∂2u

+ cos x

∂u

sin 2x

∂u

= 0 .

∂x2

∂x∂y

∂y2

∂x

∂y

Здесь a

=1,

= sin x, a

= −cos2

x . Составим и решим характеристическое урав-

x) = sin x ±1.

нение:

dy =

a ± a2

− a a

22 = sin x

sin

−

cos

Отсюда

(

y = −cos x ± x + C ,

то есть два первых интеграла характеристического уравнения имеют вид

ϕ = C1

= x − y − cos x,

Обратное

преобразование,

нужное

для нахождения производных

ψ = C2 = x + y + cos x.

ϕ/x ,

ϕ/y ,

ψ/x , ψ/y , вычисления

sin x

и cos x ,

также легко находится: 2x = ϕ + ψ x =

ϕ + ψ

192

<<< < Предыдущая 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 3031 / 3631 32 33 34 35 36 > Следующая >>>

Соседние файлы в предмете Вычислительная математика

#
26.03.20151.18 Mб99Matlab.doc
#
26.03.20158.33 Mб766шапорев выч мат.pdf