
- •1. ЭЛЕМЕНТАРНАЯ ТЕОРИЯ ПОГРЕШНОСТЕЙ; ВЫЧИСЛИТЕЛЬНЫЕ ЗАДАЧИ, МЕТОДЫ И АЛГОРИТМЫ
- •1.1. Источники и классификация погрешностей результата численного эксперимента
- •1.2. Погрешности чисел
- •1.3. Погрешности арифметических операций
- •1.4. Погрешности функций
- •1.5. Особенности машинной арифметики
- •1.6. Лабораторная работа № 1. Определение абсолютной и относительной погрешностей приближенных чисел. Оценка погрешностей результата
- •1.7. Корректность вычислительной задачи
- •1.8. Обусловленность вычислительной задачи
- •1.9. Вычислительные методы, их классификация
- •2. ПРИБЛИЖЕНИЕ ФУНКЦИЙ
- •2.1. Задача приближения функций
- •2.2. Интерполяция обобщенными многочленами
- •2.3. Полиномиальная интерполяция. Многочлен Лагранжа
- •2.4. Погрешность интерполяции
- •2.5. Конечные разности и их свойства
- •Доказательство
- •2.6. Разделенные разности и их свойства
- •2.9. Лабораторная работа № 2. Интерполирование и экстраполирование данных. Интерполяционный многочлен Лагранжа
- •2.10. Интерполяционный многочлен Ньютона с конечными разностями
- •2.11. Лабораторная работа № 3. Интерполирование и экстраполирование данных. Интерполяционный многочлен Ньютона
- •2.12. Интерполяционные формулы Гаусса, Стирлинга и Бесселя
- •3. МЕТОД НАИМЕНЬШИХ КВАДРАТОВ И СПЕЦИАЛЬНЫЕ ИНТЕРПОЛЯЦИОННЫЕ МНОГОЧЛЕНЫ
- •3.1. Постановка задачи и вывод формул метода наименьших квадратов
- •3.3. Глобальная полиномиальная интерполяция
- •3.4. Чувствительность интерполяционного многочлена к погрешностям входных данных
- •3.5. Многочлены Чебышева
- •3.6. Решение задачи минимизации оценки погрешности
- •3.8. Лабораторная работа №5. Экономизация степенных рядов
- •3.9. Локальная интерполяция
- •3.10. Сплайны, их свойства и построение
- •3.11. Погрешность приближения кубическими сплайнами
- •3.13. Тригонометрическая интерполяция. Дискретное преобразование Фурье и его реализация на ЭВМ
- •3.14. Матричная форма записи дискретного преобразования Фурье (ДПФ)
- •3.15. Алгоритм реализации ДПФ
- •3.16. Пример реализации алгоритма ДПФ при
- •3.17. Лабораторная работа № 7. Дискретное преобразование Фурье
- •4. ЧИСЛЕННОЕ ДИФФЕРЕНЦИРОВАНИЕ И ЧИСЛЕННОЕ ИНТЕГРИРОВАНИЕ
- •4.1. Простейшие формулы численного дифференцирования для первой производной
- •4.2. Формулы численного дифференцирования для второй производной
- •4.3. Формулы численного дифференцирования, основанные на интерполяции алгебраическими многочленами
- •4.4. Обусловленность формул численного дифференцирования
- •4.5. Простейшие квадратурные методы численного интегрирования
- •4.6. Оценка погрешностей простейших квадратурных формул
- •4.7. Квадратурные формулы интерполяционного типа
- •4.8. Квадратурные формулы Гаусса
- •4.9. Лабораторная работа № 8. Численное дифференцирование и численное интегрирование функций
- •5. РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ И ПРОБЛЕМЫ СОБСТВЕННЫХ ЗНАЧЕНИЙ
- •5.1. Нормы векторов и матриц и их свойства
- •5.2. Обусловленность задачи решения системы линейных алгебраических уравнений
- •5.3. Метод Гаусса (схема единственного деления)
- •5.4. Метод прогонки
- •5.5. Метод простых итераций
- •5.6. Сходимость метода простых итераций
- •5.10. Постановка задачи нахождения собственных чисел
- •5.11. Подобные матрицы
- •5.12. Локализация собственных значений
- •5.13. Степенной метод
- •5.14. Вычисление собственных векторов методом обратных итераций
- •6. ЧИСЛЕННЫЕ МЕТОДЫ РЕШЕНИЯ НЕЛИНЕЙНЫХ УРАВНЕНИЙ И СИСТЕМ
- •6.1. Решение нелинейных уравнений
- •6.2. Метод Ньютона для уравнений
- •6.3. Сходимость метода Ньютона и трудности его применения
- •6.4. Метод Ньютона решения систем нелинейных уравнений
- •6.6. Модификации метода Ньютона
- •6.7. Лабораторная работа № 11. Решение систем нелинейных уравнений методом Ньютона
- •7. ЧИСЛЕННЫЕ МЕТОДЫ РЕШЕНИЯ ЗАДАЧИ КОШИ ДЛЯ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ И СИСТЕМ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
- •7.1. Задача Коши для дифференциального уравнения первого порядка
- •7.2. Численные методы решения задачи Коши. Основные понятия и определения
- •7.3. Решение с помощью рядов Тейлора
- •7.5. Анализ ошибок, возникающих при использовании методов Рунге - Кутты
- •7.6. Методы прогноза и коррекции
- •7.7. Сравнение методов
- •7.8. Лабораторная работа № 12. Методы интегрирования обыкновенных дифференциальных уравнений
- •7.9. Решение задачи Коши для систем обыкновенных дифференциальных уравнений
- •7.11. Лабораторная работа № 13. Численное интегрирование систем дифференциальных уравнений первого порядка
- •8. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ (УРАВНЕНИЯ МАТЕМАТИЧЕСКОЙ ФИЗИКИ)
- •8.1. Классификация уравнений математической физики
- •8.2. Простейшие задачи, приводящие к дифференциальным уравнениям в частных производных
- •8.4. Уравнения параболического типа. Явные и неявные схемы
- •Доказательство
- •8.5. Уравнения гиперболического типа
- •8.6. Уравнения эллиптического типа
- •8.7. Свойства разностных схем для дифференциальных уравнений: способность аппроксимировать исходную дифференциальную задачу, устойчивость и сходимость
- •8.8. Некоторые обобщения
- •8.9. Лабораторная работа № 14. Решение задачи Дирихле для уравнения Лапласа методом сеток
- •8.10. Лабораторная работа № 15. Решение однородного уравнения колебаний струны методом сеток по неявной схеме.
3.8. Лабораторная работа №5. Экономизация степенных рядов
Пусть функция f (x) непрерывна на отрезке [a, b]. Говорят, что многочлен Pn (x) при- |
|||||||
ближает функцию f (x) равномерно на отрезке [a, b] с точностью ε, если |
|||||||
(P |
)= max |
|
f (x)− P (x) |
|
≤ ε . |
(3.8.1) |
|
|
|
||||||
n |
[a, b] |
|
|
n |
|
|
|
|
|
|
|||||
Можно поставить и решить задачу нахождения многочлена Qn (x), для которого величина |
|||||||
погрешности равномерного приближения ε |
минимальна. |
Эта задача называется задачей о |
|||||
наилучшем равномерном приближении. Теоретически доказано, что для любой непрерывной на [a, b] функции многочлен наилучшего равномерного приближения степени n существует
и он единственный.
В большинстве практических случаев задача о наилучшем равномерном приближении функции f (x) очень трудна и требует применения специально разработанных численных методов. Если же ограничиться заданной точностью ε , то можно построить многочлен, близкий к наилучшему в следующих двух случаях.
1. Если для функции f (x) ее n +1-я производная f (n+1)(x) медленно меняется на от-
резке [a, b], то интерполяционный многочлен Pn (x) с узлами, расположенными в нулях многочлена Чебышева Tn (x), близок к многочлену наилучшего равномерного приближения (см. пример в подразд. 3.7).
2. Если функция f (x) представлена на отрезке [a, b] равномерно сходящимся степен-
ным рядом |
|
f (x) = ∑∞ ak xk , |
(3.8.2) |
k =0 |
|
то на основе этого ряда можно построить многочлен минимальной степени, равномерно приближающий функцию f (x) на отрезке [a, b] с заданной точностью ε .
Рассмотрим вторую задачу более подробно. Метод ее решения называется экономизацией степенных рядов.
Пусть Pn (x)= an xn + an−1 xn−1 +... + a0 - многочлен степени n ≥1, представляющий собой отрезок ряда (3.8.2) на стандартном отрезке [−1,1]. Аппроксимируем этот многочлен много-
членом на единицу меньшей степени Qn−1 (x) наилучшего равномерного приближения. Их |
||||||||||||||||||||||
разность многочлен Rn (x)= Pn (x)−Qn−1 (x) должен удовлетворять условию |
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
max |
|
R |
(x) |
|
min . |
|
|
|
(3.8.3) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
[−1,1] |
|
|
n |
|
|
|
(x)= |
an |
T (x), для |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Как показано в подразд. 3.6, решением этой задачи является многочлен R |
n |
|||||||||||||||||||||
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2n−1 |
n |
||
|
|
|
|
|
|
|
|
|
an |
|
|
|
|
|
|
|
|
|
|
|||
которого max |
|
R |
(x) |
|
= |
|
|
. Тогда многочлен наилучшего равномерного приближения имеет |
||||||||||||||
|
|
|
||||||||||||||||||||
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||
|
[−1,1] |
|
|
n |
|
|
|
2n−1 |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
вид Q |
(x)= P (x)− |
|
an |
T |
(x). |
|
|
|
|
|
|
(3.8.4) |
||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||
n−1 |
|
|
n |
|
|
|
2n−1 |
n |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
n
Практически сначала берут отрезок ряда (3.8.2) Pn (x)= ∑ak xk , аппроксимирующий
k =0
функцию f (x) с точностью ε0 < ε . Далее степень многочлена понижают на единицу по опи-
санной процедуре. Если погрешность понижения степени P (x), равная |
ε |
1 |
= |
|
|
an |
|
|
, такова, что |
|
|
||||||||
|
|
|
|
|
|||||
n |
|
|
|
|
|
|
|
|
2n−1
ε0 +ε1 < ε, то многочлен Pn (x) заменяется многочленом (3.8.4). Затем степень Qn−1 (x) снова
78

понижают и так до тех пор, пока ε0 + ε1 + ε2 +... + εi < ε . Процесс останавливают, когда оче-
редное i +1- е понижение степени дает ε0 + ε1 + ε2 +... + εi+1 > ε. В этом случае f (x)≈Qn−i (x). Пример. Найти многочлен минимальной степени, аппроксимирующий интеграл ве-
роятности erf |
(x)= |
2 |
x |
|
−t2 dt |
на отрезке [−1,1] с точностью ε =1.5 10−3. |
|
|||||||||||
∫e |
|
|||||||||||||||||
|
|
π |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Интегралом вероятностей называют функцию y = erf (x) = |
|
|
x |
|
||||||||||||||
2 ∫e−t 2 dt = |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
π 0 |
|
|
|
|
|
|
2 |
|
4 |
|
6 |
|
|
∞ |
x |
2k −2 |
|
|
|
|
|
= |
2x 1 − x |
|
+ x |
|
− x |
|
+ ... |
= |
2x ∑ |
|
|
, |
x |
< ∞. |
|
|||
|
|
|
|
|
|
|
||||||||||||
|
|
|
1! 3 2! 5 3! 7 |
|
|
= |
(k −1)!(2k −1) |
|
|
|
(3.8.5) |
|||||||
|
|
|
|
|
|
|||||||||||||
|
π |
|
|
|
π k 1 |
|
|
|
|
|||||||||
Это знакопеременный ряд, поэтому погрешность приближения по признаку Лейбница оце-
нивается величиной ε0 , равной модулю первого отброшенного члена ряда. |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
Выберем k = 5, |
то есть оставим в ряду (3.8.5) пять членов. Тогда если |
|
x |
|
≤1, то |
|||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||||
|
2 |
|
|
|
−4 |
|
|
|
|
|
P9 (x) |
|
2x |
|
|
x |
2 |
|
x |
4 |
|
x |
6 |
|
|
|
x |
8 |
|
ε0 = |
≈ 8.5 10 |
. Таким образом, многочлен |
= |
|
|
|
+ |
|
− |
|
|
|
+ |
|
|
||||||||||||||
5! 11 |
|
|
1 − |
1! 3 |
2! 3 |
3!7 |
4! 9 |
|
|||||||||||||||||||||
|
π |
|
|
|
|
|
|
|
|
π |
|
|
|
|
|
||||||||||||||
аппроксимирует функцию y = erf (x) с точностью ε0 |
≈ 8.5 10−4 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
Понизим степень этого многочлена на единицу по формуле (3.8.4): |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
Q8 (x) = P9 |
(x)− |
a9 |
T9 (x) = 2x |
− 2x3 + |
2x5 |
− 2x7 |
+ |
2x9 |
− |
|
|
2 |
|
|
(256x9 − 576x7 + |
|
|||||||||||||
|
10 π |
216 π |
216 |
π 28 |
|
||||||||||||||||||||||||
|
|
28 |
|
|
π |
3 π |
42 π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
+ 432x5 −120x3 +9x). Здесь a9 - коэффициент при x9 |
в формуле (3.8.5), а многочлен Чебы- |
||||||||||||||||||||||||||||
шева T9 (x) посчитан по рекуррентной формуле (3.5.6). Поскольку и исходный многочлен P9 (x), и многочлен Чебышева T9 (x) содержат лишь нечетные степени аргумента, то в ре-
зультате проведенной процедуры степень исходного многочлена понизится на две единицы. В результате получим
|
|
|
|
Q7 (x)= |
|
1 |
6143 |
x |
− |
|
763 |
x |
3 |
+ |
|
59 |
x |
5 |
|
− |
|
3 |
|
x |
7 |
|
|
|
|
(3.8.6) |
|||||||||||||||
|
|
|
|
|
|
3072 |
1152 |
|
|
|
320 |
|
|
112 |
. |
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
Понижение степени многочлена |
|
P9 (x) |
|
|
сопровождается дополнительной погрешно- |
||||||||||||||||||||||||||||||||||||||
стью |
(3.8.3) ε1 = |
|
a9 |
= |
|
|
2 |
|
|
≈ |
|
1 |
|
|
|
= 0.2 10−4 . Тогда |
ε0 |
+ ε1 = 8.7 10−4 < ε , то есть |
|||||||||||||||||||||||||||
|
28 |
|
|
π |
28 |
49005 |
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
216 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
многочлен наилучшего равномерного приближения Q7 (x) |
обеспечивает заданную точность |
||||||||||||||||||||||||||||||||||||||||||||
аппроксимации. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
Возможно ли дальнейшее понижение степени? При этом величина дополнительной |
|||||||||||||||||||||||||||||||||||||||||||
погрешности будет ε2 = |
a7/ |
= |
|
|
3 |
|
|
|
≈ 2.3 10 |
−4 |
|
. Суммарная погрешность возрастет до |
|||||||||||||||||||||||||||||||||
26 |
|
|
π 26 |
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
112 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
ε0 |
+ ε1 + ε2 =1.1 10−3 |
< ε, поэтому возможно дальнейшее понижение |
степени многочлена |
||||||||||||||||||||||||||||||||||||||||||
Q7 |
(x). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Итак, по формуле (3.8.4) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Q5 |
(x)= Q7 (x)− |
a7/ |
T7 (x)= |
1 |
6143 |
x |
− |
|
763 |
|
|
x |
3 |
+ |
|
59 |
x |
5 |
− |
|
|
3 |
|
x |
7 |
|
+ |
3 |
|
× |
|||||||||||||||
|
|
|
|
|
|
3072 |
1152 |
|
|
320 |
|
|
112 |
|
|
|
|
||||||||||||||||||||||||||||
2 |
6 |
|
|
|
|
|
|
|
112 π |
26 |
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
× (64x |
7 |
−112x |
5 |
+ 56x |
3 |
− 7x) |
= |
|
1 |
|
|
3067 |
x |
− |
|
23 |
x |
3 |
+ |
11 |
x |
5 |
= |
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
1536 |
|
36 |
|
80 |
|
|
(3.8.7) |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
π |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
= 1.126543x − 0.360454x3 + 0.077576x5 .
79

Дальнейшее понижение степени многочлена наилучшего равномерного приближения
в пределах заданной точности |
ε =1.5 10−3 |
невозможно, ибо ошибка при таком понижении |
||||
составит: |
ε3 |
= |
11 |
≈ 4.8 |
10−3 . Тогда |
ε0 + ε1 + ε2 + ε3 ≈ 6.0 10−3 > ε . Поэтому реше- |
|
|
80 |
π 24 |
|
|
|
нием задачи является многочлен (3.8.7).
Выполним теперь эти же действия средствами пакета Mathcad, при этом, как и в лабораторной работе №2, воспользуемся меню Symbolics (Символьные вычисления). Это меню содержит операции символьной математики. Пункт Evaluate (Вычислить) содержит три опе-
рации: Symbolically (Символьно), Floating Point (С плавающий запятой) и Complex (Ком-
плексное).
Строкой Simplify (Упростить) мы уже пользовались во второй лабораторной работе. Совершенно аналогично после щелчка по Expand (Развернуть) в выделенном выражении раскрываются скобки, после щелчка по кнопке Factor (Разложить на множители) выделенное выражение раскладывается на множители, наконец, результатом щелчка по кнопке Collect (Собрать) является приведение подобных членов в выделенном выражении.
Итак, наберем в рабочем документе
ORIGIN :=1 |
|
|
|
|
|
|
|
|
|
|
|
P9(x):= 2 |
x |
|
− |
x2 |
+ |
x4 |
− |
x6 |
+ |
x8 |
|
π |
1 |
3 1 |
5 2 |
7 6 |
9 24 |
|
|||||
|
|
|
|
|
|
|
|||||
После щелчка по кнопкам Symbolics→Expand ниже определенной функции появится выражение
2 |
x |
− |
2 |
|
x3 |
+ |
1 |
|
x5 |
− |
1 |
|
x7 |
+ |
1 |
|
x9 |
. |
|
π |
3 |
π |
5 |
π |
21 |
π |
108 |
π |
|||||||||||
|
|
|
|
|
|
|
|
|
|
Числовые коэффициенты этого выражения можно представить в десятичной форме. Для этого выберем операции с плавающий запятой: Symbolics → Evaluate→Floating Point. Появится дополнительное меню:
Зададим в маленьком окошечке этого меню, например, девять значащих чисел после запятой. После щелчка по кнопке OK в рабочем документе появится выражение исходного многочлена в виде
1.12837917 x −0.37612639 x3 + 0.112837917 x5 −0.0268661707 x7 + 0.00522397763 .
Для вычисления многочленов Чебышева в пакете Mathcad имеются две функции: Tcheb(n,x) и Ucheb(n,x). К сожалению, они становятся встроенными в Mathcad лишь после подгрузки соответствующего электронного учебника. В меню Insert (Вставить) имеется кнопка подменю Function (Функция), которая открывает окно диалога списка встроенных функций пакета. В этом списке Tcheb и Ucheb отсутствуют.
Однако многочлены Чебышева определяются разными способами (см. формулы (3.5.3) – (3.5.8)). Среди них есть очень простые и легко программируемые определения. Воспользуемся, например, формулами (3.5.3) и (3.5.8).
Введем с клавиатуры
T 9(x):= |
1 |
(x + |
x2 −1)9 + (x − |
x2 −1)9 |
|
2 |
|
|
|
80

Выделим введенное выражение правым нижним синим углом, тогда после нажатия клавиш
Symbolics→Expand получим
256 x9 −576 x7 |
+ 432 x5 |
−120 x3 + 9 x |
|
|||||
Далее |
9 |
|
|
|
Γ(9 − m) |
|
|
|
T 99(x):= |
∑4 (−1)m |
|
(2 x)9−2 m |
|||||
2 |
Γ(m |
+1) Γ(9 − 2 m +1) |
||||||
|
m=0 |
|
|
|||||
Здесь Γ(n +1)= n!-гамма–функция, имеющаяся в окне диалога списка встроенных функций
под именем Gamma. Аналогично, после нажатия клавиш Symbolics→Evaluate →Symbolically будет получено то же выражение:
256 x9 −576 x7 + 432 x5 −120 x3 +9 x
Выполним следующие действия лабораторной работы:
ε0 := |
2 |
Γ(6) |
ε0 = 8.548 10 |
−4 ε1 := |
2 |
|
ε1 = 2.041 10−5 |
|
π 11 |
π 216 |
2 |
||||||
|
|
|
8 |
Q7(x):= P9(x)− ε1 T 9(x)
Symbolics→Expand
30726143 xπ −1152763 xπ3 + 32059 xπ5 −1123 xπ7 Symbolics→Evaluate→Floating Point
1.12819551 x −0.37367765 x2 + 0.104022455 x5 −0.015112221 x7
α1 := ε0 + ε1 |
α1 = 8.752 10−4 |
|
α2 := α1 + ε2 |
α2 =1.111 10−3 |
|
T 7(x):= 1 |
(x + x2 −1)7 + (x − |
|
2 |
|
|
Symbolics→Expand
64 x7 −112 x5 + 56 x3 − 7 x
Q5(x):= Q7(x)+ ε2 T 7(x)
ε2 := |
3 |
ε2 = 2.361 10−4 |
|
π 112 26 |
|
x2 −1)7
Symbolics→Expand
3067 |
|
x |
− |
23 |
|
x3 |
+ |
11 |
|
x5 |
|
1536 |
π |
36 |
π |
80 |
π |
||||||
|
|
|
|
|
|||||||
Symbolics→Evaluate→Floating Point |
|||||||||||
1.12654261 x − 0.360454457 x3 + 0.0775760678 x5 |
|||||||||||
ε3 := |
|
11 |
|
|
ε3 = 4.849 10−3 |
||||||
80 |
|
π 24 |
|||||||||
|
|
|
|
|
|
||||||
α3 := α2 + ε3 |
α3 = 5.96 10−3 |
||||||||||
Задание №1. Для приведенных функций f (x) построить многочлен наилучшего равномерного приближения на отрезке [−1,1], выбрав число членов исходного аппроксимирующего полинома по заданной точности ε:
1. |
f (x)= sin x = ∑∞ (−1)k |
|
|
|
x2k +1 |
|
|
, |
|
|
x |
|
< ∞, ε =10−3. |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
k =0 |
|
|
|
(2k +1)! |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
2. |
f (x)= cos x = ∑∞ (−1)k |
|
|
x2k |
, |
|
|
x |
|
< ∞, ε =10−3. |
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
k =0 |
|
|
|
|
(2k )! |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
f (x)= tg x = x + |
x3 |
|
|
2 |
|
|
|
17 |
62 |
|
|
125762 |
|
|
|
π |
|
||||||||||||
3. |
|
+ |
|
x5 + |
|
|
x7 + |
|
x9 |
+ |
|
|
x11 +..., |
x |
< |
|
, |
|||||||||||||
3 |
15 |
|
315 |
2835 |
14189175 |
2 |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ε = 5 10−4. |
|
|
|
|
|
|
|
|
|||||||
81
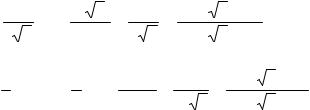
4. f (x)= ctg x = |
1 |
− |
x |
− |
x3 |
− |
2 |
x5 |
− |
1 |
x7 |
− |
2 |
x9 |
+..., |
|
x |
|
< π, |
|
|
|
|||||||||||||||||||
x |
3 |
45 |
945 |
|
4725 |
93555 |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
ε =10 |
−4. |
|
|
|
|
|
|
|
|
||||
5.f (x)=
6.f (x)=
7.f (x)=
8.f (x)=
9.f (x)=
sec x = 1 + |
x 2 |
+ |
5 |
x4 + |
61 |
x6 + |
277 |
x8 + |
50521 |
x10 + ..., |
|
x |
|
< |
π |
, |
|
|
|
||||||||||||||||
|
|
|
|
|
|
||||||||||||
2 |
|
24 |
|
720 |
|
8064 |
|
3628800 |
|
|
|
|
|
2 |
|
||
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
ε = 1.5 10−3. |
|
|
|
|
|
|
|
|
|
|||
cosecx = |
1 |
+ |
x |
|
+ |
|
|
7 x3 |
|
+ |
|
|
31 |
|
x |
5 + |
|
|
|
|
127 |
x7 |
+ |
|
511 |
x9 + ..., |
|
x |
|
< π, |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
x |
6 |
|
|
|
360 |
|
|
15120 |
|
|
|
|
|
604800 |
|
|
23950080 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ε = 10−4. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
x3 |
|
|
|
|
|
x5 |
|
|
|
∞ |
|
x2k +1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
shx = x + |
|
|
|
+ |
|
|
|
|
|
+... + ∑ |
|
|
|
|
|
+..., |
|
x |
|
< ∞, |
ε =10−3. |
|
|
|
|
|
|
|
|
|
|
||||||||||||||
3! |
|
5! |
|
(2k + |
1)! |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
k =0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
x2 |
|
|
|
|
|
|
x4 |
|
|
|
∞ |
|
x2k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
ch x =1 + |
|
|
|
|
+ |
|
|
|
|
|
+... + ∑ |
|
|
|
+..., |
|
|
x |
< ∞, |
ε =10−3. |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
2! |
|
|
4! |
|
|
|
(2k )! |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
k =0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
th x = x − |
|
x3 |
|
|
+ |
|
2 |
|
|
x5 − |
17 |
|
|
x7 + |
62 |
|
|
|
x |
9 − |
|
125762 |
|
x11 +..., |
|
x |
|
< |
π |
, |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
3 |
|
|
15 |
|
|
315 |
|
2835 |
|
|
|
14189175 |
|
|
2 |
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ε = 5 10−4. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
f (x)= cth x = |
1 |
|
|
x |
|
|
x3 |
2 |
|
x5 − |
|
|
1 |
|
|
|
x7 + |
|
2 |
|
x9 |
|
|
|
x |
|
|
|
|
|
|
||||||||||||||||||||||||||||
10. |
|
|
+ |
|
|
|
− |
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+..., |
< π, |
|
|
|
||||||||||||||||||||||||||
x |
3 |
45 |
945 |
4725 |
93555 |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ε =10−4. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
f (x)= sec hx = |
|
|
1 |
|
|
|
= |
1 − |
x2 |
+ |
5 |
x4 |
− |
|
|
61 |
|
|
x6 |
+ |
1385 |
x8 − |
50521 |
x10 |
+..., |
|
|
|
|||||||||||||||||||||||||||||||
|
|
ch x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
11. |
|
|
|
|
|
|
|
|
2! |
|
|
|
4! |
|
|
|
|
6! |
|
|
|
|
|
|
8! |
|
|
|
|
|
10! |
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
< |
|
π , ε =1.5 10−3. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
12. |
f (x)= cschx = |
|
|
|
1 |
|
|
|
= |
1 |
− |
x |
+ |
|
7 x3 |
− |
|
|
|
|
31 |
x5 |
+ |
127 |
|
x7 |
− |
|
|
511 |
|
x9 |
+..., |
|||||||||||||||||||||||||||
|
sh x |
x |
|
360 |
15120 |
604800 |
23950080 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
< π, |
ε =10−4. |
|
|
(−1)k |
|
|
|
|
|
|
|
|
|
|||||||||||||||||
13. |
f (x) = |
1 |
arctg |
|
x |
2 |
+ |
1 |
|
|
|
ln 1 + x |
|
|
2 + x 2 |
= ∑∞ |
|
x 4k +1 , |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
2 |
1 − x 2 |
4 |
|
2 |
|
|
|
2 + x 2 |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
1 − x |
|
|
|
k =0 4k +1 |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
≤ 1, |
|
ε = 10−3. |
|
|
3 + x2 = |
|
|
(−1)k |
|
|
|
|
|
||||||||||||||||||||||||||||||
14. |
f (x)= |
1 arctg x + |
1 arctg |
|
|
|
x |
|
|
+ |
|
1 |
|
|
|
|
|
ln 1 + x |
∑∞ |
|
x6k +1 |
, |
|
|
||||||||||||||||||||||||||||||||||||
− x2 |
|
|
|
|
3 |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
3 |
|
|
|
|
|
6 |
|
|
|
|
|
1 |
12 |
|
|
|
|
|
|
1 − x |
3 + x2 |
k =0 6k +1 |
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
≤ 1, ε = 1.5 10−3. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
15. |
f (x)= x + (1 − x)ln(1 − x)= ∑∞ |
|
|
|
xk +1 |
|
, |
|
|
x |
|
≤1, ε =10−3. |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k =1 k(k + |
1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
16.f (x)=
17.f (x)=
18.f (x)=
19.f (x) =
|
x |
+ |
|
x2 |
|
+ |
1 |
(1 − x2 )ln(1 − x)= ∑∞ |
|
|
xk +2 |
|
, |
|
|
x |
|
≤1, ε =10−3. |
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
2 4 2 |
|
|
|
|
|
|
k =1 k(k + |
2) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
3x2 |
− |
x |
− |
1 |
(1 − x2 )ln(1 − x)= ∑∞ |
|
|
|
xk +2 |
|
|
|
|
|
, |
|
|
|
x |
|
≤1, ε = 5 10−4. |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
4 |
|
|
|
2 2 |
|
|
|
|
|
k =1 k(k +1)(k + 2) |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
1 |
[11x3 −15x2 + 6x + 6(1 − x)3 ln(1 − x)]= ∑∞ |
|
|
|
|
|
|
|
|
xk +3 |
|
|
, |
|||||||||||||||||||||||||||||
36 |
|
|
|
|
|
|
|
|
|
2)(k + 3) |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
x |
|
≤1, ε =10−4. |
|
|
|
|
|
k =1 k(k +1)(k + |
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
4 |
3 |
|
|
|
x |
|
|
|
|
(k!) |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
+ 4x(4 − x2 )− |
|
arcsin |
= |
∑∞ |
|
|
|
x2k , |
|
x |
|
< 2, ε = 10−3. |
|
||||||||||||||||||||||||||||
|
2 |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
4 − x2 |
|
|
|
|
|
|
|
|
2 |
|
|
|
k =0 (2k )! |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
1 |
|
|
∞ |
2 |
|
|
|
|
|
|
|
20. f (x)= 4(4 − x2 )− |
|
arcsin |
x |
= ∑ |
(k!) |
|
x2k +1 , |
|
x |
|
< 2, ε =10−3. |
|
2 |
|
|
||||||||||
2 |
(2k +1)! |
|||||||||||
|
|
|
k =0 |
|
|
|
|
|
||||
82
