7.5. Анализ ошибок, возникающих при использовании методов Рунге - Кутты

Рассмотрим общую идею группы методов, известных в литературе под названием «методов прогноза и коррекции». Как ясно из названия, вначале «предсказывается» значение yn+1 , а затем используется тот или иной метод для «корректировки» этого значения. Эту же

формулу можно использовать сколько угодно раз для повторной корректировки уже скорректированного значения yn+1 .

Для демонстрации основных идей метода можно использовать для прогноза формулу

где индекс (0) означает исходное приближение к yn+1 . Непосредственно из написанной формулы следует, что с ее помощью нельзя вычислить, например, y1 , ибо для этого потребовалась бы точка, расположенная перед начальной точкой y0 . Чтобы начать решение по методу

прогноза и коррекции, часто используется метод Рунге - Кутты.

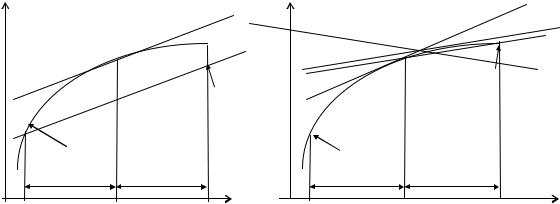
Геометрически предсказание сводится к тому, что находится угол наклона касательной в точке (xn , yn ) (см. левый рисунок). После этого через точку (xn−1 , yn−1 ) проводится

Вычислим наклон касательной в точке (xn+1 , yn(0+)1 ). Эта касательная изображена на правом ри-

В общем случае i -е приближение, очевидно, будет находиться таким образом:

К настоящему времени разработано много методов прогноза и коррекции разных порядков, обеспечивающих очень большую точность решения. В некоторых из них по заданной точностипредусмотренавтоматическийвыбор шага и автоматический выбор порядка метода.

170

7.7. Сравнение методов

а). Методы Рунге - Кутты.

1.В этих методах используется информация только об очередной точке решения, поэтому с их помощью можно начинать решение.

2.По той же самой причине приходится многократно вычислять функцию f (x, y).

3.Методы этой группы позволяют очень легко менять величину шага h.

4.При использовании этих методов трудно получить оценку ошибки интегрирования. б). Методы прогноза и коррекции.

1. Так как в этих методах используется информация о ранее вычисленных точках решения, то с их помощью нельзя начать решение.

2. Из-за использования информации о ранее вычисленных точках методы этой группы более экономичны по затратам машинного времени.

3. При любом изменении величины шага h приходится временно возвращаться к методам Рунге - Кутты.

4. В качестве побочного продукта вычислений получается хорошая оценка ошибки интегрирования.

Как всегда, наиболее целесообразным является использование при решении практи-

y(0)= 0, a =1.4, b = 2.6.

Она заполняется следующим образом.

1. Записываем в первой строке x0 , y0 , вычисляем f (x0 , y0 ) и заносим в таблицу в качестве k0(1).

171

- трех сотых. В противном случае шаг h следует уменьшить.

7.8. Лабораторная работа № 12. Методы интегрирования обыкновенных дифференциальных уравнений

Существует большое число методов приближенного решения дифференциальных уравнений, основанных на самых различных идеях. Численные методы дают приближенное решение y(x) в виде таблицы значений y1 , y2 ,..., yn в точках x1 , x2 ,..., xn .

Простейшим методом численного интегрирования дифференциального уравнения первого порядка y/ = f (x, y), удовлетворяющего начальному условию y(x0 )= y0 , является метод Эйлера. В нем величины yi вычисляются по формуле

xi = x0 + ih, i = 0,1,2,...

yi+1 = yi + hf (xi , yi ).

172

Метод Эйлера относится к группе одношаговых, в которых для расчета точки (xi+1 , yi+1 ) требуется информация только о последней вычисленной точке (xi , yi ). Геометри-

ческая интерпретация метода изложена в подразд. 7.4.

В среде Mathcad имеется тринадцать встроенных функций решения дифференциальных уравнений и систем ( задача Коши, краевая задача, уравнения в частных производных). Самая употребительная из них - rkfixed, в которую заложен метод Рунге – Кутты четвертого порядка с постоянным шагом. Подпрограммы для метода Эйлера нет из-за его низкой точности. Формулы метода Эйлера настолько просты, что вычисления по ним можно организовать

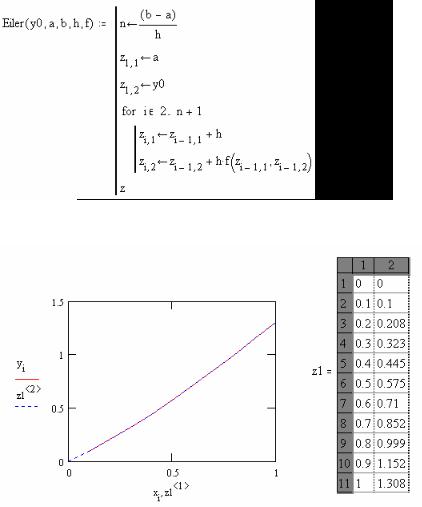
Аналогичного результата можно достигнуть, введя подпрограмму, реализующую формулы (7.4.1) метода Эйлера:

z1:= Eiler(y0,0,1,0.1, f )

173

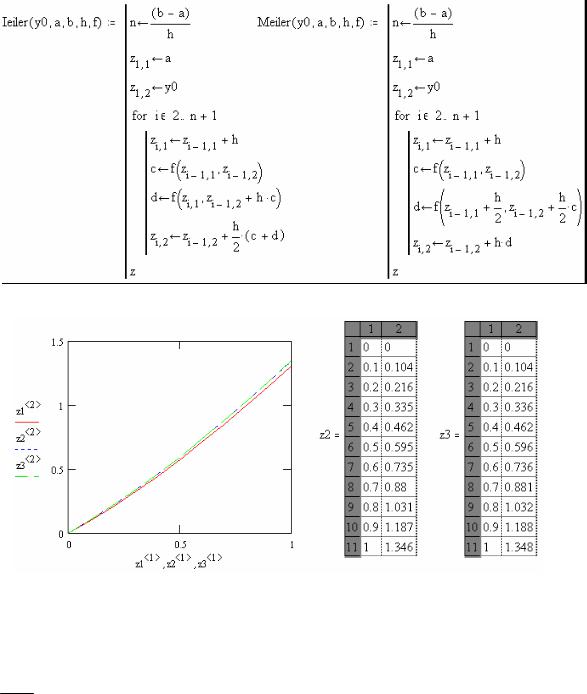
Минимальная переделка подпрограммы позволяет запрограммировать исправленный и модифицированный метод Эйлера по формулам (7.4.4) и (7.4.6).

z2 := Ieiler(y0,0,1,0.1, f ) z3 := Meiler(y0,0,1,0.1, f )

Обратимся теперь к средствам пакета Mathcad. Для решения обыкновенных «неособенных» дифференциальных уравнений здесь используются две функции rkfixed и Rkadapt,

h = b −n a , f (x, y)- правая часть дифференциального уравнения. Несмотря на то что при ре-

шении дифференциального уравнения функция Rkadapt использует переменный шаг, она

Обращение к rkfixed с h1 = 0.1 и h2 = 0.05 сделано для оценки погрешности интег-

рирования по правилу Рунге (7.5.2). errRKF - оценка погрешности.

На данном учебном примере, конечно, невозможно оценить выгоды использования функции Rkadapt вместо rkfixed. В более сложных случаях Rkadapt решает уравнение более точно и быстро. Даже в этом примере точность решения по Rkadapt выше, чем по rkfixed. Это видно из следующей таблицы:

В заключение приведем подпрограмму RGK, реализующую формулы (7.4.13) метода Рунге – Кутты четвертого порядка. Далее, как и в предыдущем случае, произведена оценка погрешности по правилу Рунге и даны графики полученных решений. Программа метода Рунге – Кутты четвертого порядка (RGK) приведена после графиков проинтегрированных функций.

z6 := RGK (y0,0,1,0.1, f ) z7 := RGK (y0,0,1,0.05, f ) i := 1...10 Er2i := (z6 2 )i − (z7 2 )2 i

errRGK := max(Er2)

15

Задание № 1. Решить заданное дифференциальное уравнение первого порядка методом Эйлера и Рунге – Кутты четвертого порядка на отрезке x [0,1] с шагом h = 0.1 и оце-