2. ПРИБЛИЖЕНИЕ ФУНКЦИЙ
2.1. Задача приближения функций
Вычисление значений функции y = f (x) - задача, с которой постоянно приходиться сталкиваться на практике. Часто бывает, что вычисление f (x) затруднительно, например:
1)функция y = f (x) задана таблично yi = f (xi ), i =1,n , а вычисление необходимо проводить в точках x , не совпадающих с табличными;
2)вычисление функции y = f (x) дорого;
3)для вычисления y = f (x) необходим эксперимент.
В таких условиях целесообразно заменить f (x) некоторой близкой к ней функцией g(x), которая вычисляется быстро и надежно, а погрешность приближения f (x)− g(x) достаточно мала. При этом полезно при выборе функции g(x) использовать любую дополнительную информацию о функции f (x), о ее гладкости, четности, периодичности, монотонности и так далее. Это дает возможность осознанно выбрать класс G аппроксимирующих функций.
Широко используются функции вида Φm (x)= a0ϕ0 (x)+ a1ϕ1 (x)+... + amϕm (x), представляющие собой линейные комбинации некоторых базисных функций
ϕ0 (x), ϕ1 (x),...,ϕm (x). Функция Φm (x) называется обобщенным многочленом степени m .
2.2.Интерполяция обобщенными многочленами
Если ставится требование совпадения функции |
g(x) с функцией f (x) |
в некоторых |
||||||||||||||||||||||||||
фиксированных точках, то это приводит к задаче интерполяции. |
|
|
g(x), удов- |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
f (x) |
|
|
|
|
|
|
|
|
|
|
Построить функцию |
|||||||||
|
|
|
|
|
|
- |
|
|
|
|
|
|
|
летворяющую условиям |
g(xi )= yi , |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i = 0,1,..., n. |
xi - узлы интерполяции. |
|||||||
|
|
|
|
|
|
|
|
y = g(x) |
|
|
|
|
|
|
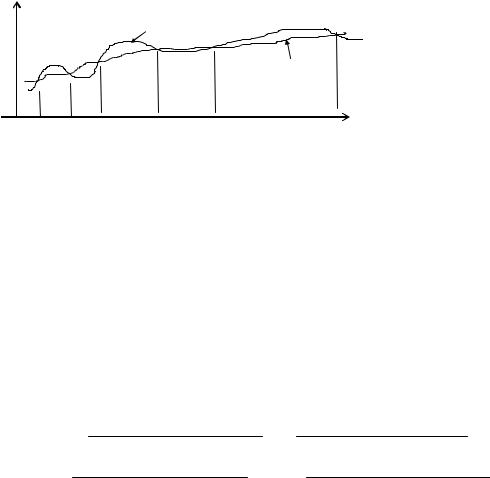
Очевидно, |
что выбор |
g(x) неодноз- |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
чен, |
|
так как по заданной табли- |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
це |
можно |
построить |
бесконечно |
||||||
x0 x1 |
|
x2 |
x3 |
|
|
|
|
x4 ... |
|
xn |
|
|
|
много интерполирующих функций. |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Рассмотрим обобщенный |
многочлен |
|
Φm (x), |
|
|
удовлетворяющий |
условию |
|||||||||||||||||||||
Φm (xi )= yi , |
i = |
|
. |
|
|
|
|
Эта |
|
|
|
формула, |
|
|
|
|
представленная |
в |
виде |
|||||||||
0, n |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
Φm (x)= a0ϕ0 (x)+ a1ϕ1 (x)+... + amϕm (x), очевидно, |
эквивалентна следующей системе линей- |
|||||||||||||||||||||||||||
ных алгебраических уравнений: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
ϕ0 (x0 )a0 |
+ ϕ1 |
(x0 )a1 +... + ϕm |
(x0 )am = y0 , |
|
|
|
|||||||||||||||||||
|
|
|
|
ϕ |
0 |
(x |
)a |
0 |
+ ϕ |
(x |
)a +... + ϕ |
m |
(x |
|
)a |
m |
= y |
, |
|
|
|
|||||||
|
|
|
|
|
|
|
1 |
|
1 |
|
1 |
1 |
1 |
|
|
1 |
|
|
|
(2.2.1) |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
................................................................. |
|
|
|
|
|||||||||||||||||||||
|
|
|
ϕ |
0 |
(x |
n |
)a |
0 |
+ ϕ |
(x |
n |
)a +... + ϕ |
m |
(x |
n |
)a |
m |
= y |
n |
. |
|
|
|
|||||
|
|
|
|
|
|
|
|
1 |
|
1 |
|
|
|
|
|
|
|
|
|
|||||||||
Для определения Φm (x) необходимо решить систем (2.2.1) относительно a0 , a1,..., am . На практике это делается чрезвычайно редко. Как правило, система (2.2.1) плохо обусловле-
25
на. В большинстве приложений используются специальные явные формулы для записи |
||||||||||
Φm |
(x) |
и вычисление {am } |
не нужно. |
|
|
|
|
|||
|
|
|
|
|
2.3. Полиномиальная интерполяция. Многочлен Лагранжа |
|
||||
{ϕ |
|
|
Если |
в качестве |
базисной |
взять систему степенных функций, |
то есть |
|||
0 |
,ϕ ,...,ϕ |
n |
}→ {1, x, x2 ,..., xn }, то получаем задачу полиномиальной интерполяции: |
|
||||||
|
1 |
|
|
|
|
|
|
|
||
|
|
|
|
|
Pn (x)= ∑n ak xk , |
Pn (xi )= yi , i = |
|
. |
(2.3.1) |
|
|
|
|
|
|
0, n |
|||||
|
|
|
|
|
|
k =0 |
|
|
|
|
Теорема 2.1. Существует единственный интерполяционный многочлен степени n , удовлетворяющий условиям (2.3.1).
В качестве искомого многочлена возьмем многочлен степени n вида |
|
|
Pn (x)= a0 (x − x1 )(x − x2 )...(x − xn )+ a1 (x − x0 )(x − x2 )...(x − xn )+ |
(2.3.2) |
|
+ a2 (x − x0 )(x − x1 )(x − x3 )...(x − xn )+... + an (x − x0 )(x − x1 )...(x − xn−1 ). |
||
|
Таким образом, система функций, по которой строится интерполяционный многочлен, есть
ϕ0 (x)= (x − x1 )(x − x2 )...(x − xn ),
ϕ1 (x)= (x − x0 )(x − x2 )...(x − xn ),
|
|
|
................................................... |
|
|
|||||||||||||
|
|
|
ϕn (x)= (x − x0 )(x − x1 )...(x − xn−1 ). |
|
||||||||||||||
|
|
f (x) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Для нахождения Pn (x) надо |
|
|
|
|
|
|
|
Pn (x) |
|
|
|
|
|
|
|
найти набор коэффициентов |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a0 , a1,..., an . Не будем |
сос- |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
тавлять и решать систему |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
линейных уравнений |
вида |
x0 x1 |
x2 |
x3 |
x4 ... |
|
|
|
|
xn |
|
|
|
|
|
(2.2.1), найдем коэффициен- |
||||
|
|
|
|
|
|
|
|
|
ты иным способом. |
|
||||||||
Пусть |
x = x0 , с учетом |
Pn (x0 )= y0 |
= a0 (x0 − x1 )(x0 − x2 )...(x0 − xn ), получим |
|
||||||||||||||
|
|
|
a0 = |
|
|
|
|
|
y0 |
|
|
|
|
|
|
|
. |
|
|
|
|
(x |
0 |
− x |
)(x |
0 |
− x |
2 |
)...(x |
0 |
− x |
n |
) |
|
|||
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|||||
Аналогично, |
полагая x = x1 и учитывая, что |
y1 |
= a1 (x1 − x0 )(x1 − x2 )...(x1 − xn ), |
будем |
||||||||||||||
иметь
Если x = xn , то иметь вид
|
a1 |
= |
|
|
|
|
|
|
|
|
|
y1 |
|
|
|
|
|
|
|
|
. |
|
|
(x |
− x |
0 |
)(x |
− x |
2 |
)...(x |
− x |
n |
) |
||||||||||||
|
|
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
1 |
|
|
|
|
|||
an = |
|
|
|
|
|
|
|
|
|
yn |
|
|
|
|
|
|
|
. Тогда сам многочлен Pn (x) будет |
||||
(x |
n |
− x |
0 |
)(x |
n |
− x |
)...(x |
n |
− x |
n−1 |
) |
|||||||||||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
||||||
(2.3.3)
Эта формула называется интерполяционной формулой Лагранжа. Приведем ее в сокращенной записи:
26
|
|
Pn (x)= Ln (x)= ∑n y j ln j (x), |
|
|
|
||
|
|
|
|
j=0 |
|
|
|
ϕn j = ln j (x)= ∏n |
x − xk |
= |
(x − x0 )(x − x1 )...(x − x j−1 )(x − x j+1 )...(x − xn ) |
|
. |
(2.3.4) |
|
|
|
|
|
|
|||
k =0, x j − xk |
|
(x j − x0 )(x j − x1 )...(x j − x j−1 )(x j − x j+1 )...(x j − xn ) |
|
||||
k ≠ j |
|
|
|
|
|
|
|
Очевидно, ln j (x) представляет собой многочлен степени n , удовлетворяющий усло- |
|||||||
вию |
|
|
)= 1, i = j, |
|
|
|
|
|
|
|
ln j (xi |
|
|
|
|
|
|
|
|
0, i ≠ j. |
|
|
|
Таким образом, степень многочлена |
Ln (x) равна n , при x = xi в формуле (2.3.4) об- |
||||||
ращаются в нуль все слагаемые, кроме слагаемого с номером j = i , равного |
y j . |
|
|||||
Выпишем отдельно многочлены Лагранжа первой и второй степени, ибо именно они чаще всего используются на практике.
|
|
|
|
|
|
|
L (x) |
= y |
|
|
x − x1 |
|
|
+ y |
x − x0 |
− прямая, |
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
1 |
|
|
|
0 |
|
x |
0 |
− x |
|
|
1 |
x − x |
0 |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
(x − x1 )(x − x2 ) |
|
|
|
|
|
1 |
|
|
|
1 |
|
|
|
|
|
|
(x − x0 )(x |
− x1 ) |
|
|
|||||||||||||
L (x)= y |
|
|
+ y |
|
(x − x0 )(x − x2 ) |
|
+ y |
|
|
− парабола. |
|||||||||||||||||||||||||
|
|
) |
|
|
|
|
|||||||||||||||||||||||||||||
2 |
0 (x |
0 |
− x |
)(x |
0 |
− x |
2 |
|
1 |
|
(x − x |
0 |
)(x − x |
2 |
) |
|
|
|
2 |
(x |
2 |
− x |
0 |
)(x |
2 |
− x ) |
|
||||||||
|
|
|
1 |
|
|
|
|
|
|
|
|
1 |
1 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|||||||||
Пример. Написать интерполяционный многочлен Лагранжа для функции чения которой заданы таблицей
|
i |
|
|
|
0 |
|
|
|
|
1 |
|
|
|
|
2 |
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
xi |
|
|
|
0 |
|
|
|
0.1 |
|
|
|
0.3 |
|
|
|
0.5 |
|
|||
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
yi |
|
|
-0.5 |
|
|
|
0 |
|
|
|
0.2 |
|
|
|
1.0 |
|
||||
|
|
|
|
|
|
|
|
|
|
||||||||||||
(2.3.5)
f (x), зна-
В данном случае n = 3, получаем при интерполяции кубическую параболу. Вычислим |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
вначале |
ln j (x): |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
l3,0 |
= |
(x − x |
|
)(x − x |
2 |
)(x − x |
3 |
) |
|
= |
(x − 0.1)(x − 0.3)(x − 0.5) |
= |
|
x3 |
− 0.9x2 |
+ 0.23x − 0.015 |
. |
||||||||||||||||||||||||||||||||||||||||||
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
(x |
0 |
− x |
)(x |
0 |
− x |
2 |
)(x |
0 |
− x |
3 |
) |
(0 − 0.1)(0 − 0.3)(0 − 0.5) |
|
|
|
|
|
|
|
|
|
0.015 |
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
l3,1 |
≠ 0 , но его значение не понадобится, так как |
|
y1 = 0 . Не будем его вычислять. |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
l3,2 |
|
|
|
|
|
|
(x − 0)(x − 0.1)(x − 0.5) |
|
|
x3 − 0.6x2 |
+ 0.05x |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
= − |
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
(0.3 |
− 0)(0.3 − 0.1)(0.3 − 0.5) |
|
|
|
0.012 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
l3,3 |
|
|
|
|
|
|
|
(x − 0)(x − 0.1)(x − 0.3) |
x3 − 0.4x2 + 0.03x |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
= |
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
(0.5 − 0)(0.5 − 0.1)(0.5 − 0.3) |
|
|
|
|
0.04 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
Тогда искомый интерполяционный многочлен Лагранжа третьей степени будет вы- |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
глядеть так |
L |
(x)= l |
3,0 |
y |
0 |
|
+ l |
3,1 |
y |
|
+ l |
3,2 |
y |
2 |
+ l |
3,3 |
y |
3 |
= 41.67x3 − 30.00x2 |
+ 7.58x − 0.50. |
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2.4. Погрешность интерполяции |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
Теорема 2.2. Пусть функция |
|
f (x) |
дифференцируема n +1 раз на отрезке [a, b], |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
содержащем узлы интерполяции |
xi , i = |
|
. |
Тогда для погрешности интерполяции в |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
0, n |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
точке |
x [a, b] |
|
справедливо |
|
|
равенство |
|
|
f (x)− P (x) |
= |
|
f (n+1)(ζ) |
ω |
|
|
(x), |
в |
котором |
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
(n +1)! |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
ωn+1 (x)= (x − x0 )(x − x1 )(x − x2 )...(x − xn ), а ζ (a, b). |
|
|
n |
|
|
|
|
|
n+1 |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
Последнюю |
|
|
формулу |
|
|
|
|
несколько |
|
|
|
модернизируют. |
|
Так |
|
|
|
как |
положение |
||||||||||||||||||||||||||||||||||||||||
точки |
ζ |
|
|
неизвестно, |
|
|
|
|
то |
|
|
|
|
|
f (n+1)(ζ) |
|
заменяют |
|
|
на |
|
|
M |
n+1 |
= max |
|
f (n+1)(x) |
|
. |
Тогда |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
27 |
|
|
|
|
|
|
|
|
|
|
|
|
[a, b] |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||