4.7. Квадратурные формулы интерполяционного типа

4.8. Квадратурные формулы Гаусса

4.9. Лабораторная работа № 8. Численное дифференцирование и численное интегрирование функций

Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Балтийский государственный технический университет "ВОЕНМЕХ" им. Д.Ф. Устинова

Предмет:

Вычислительная математика

Файл:

шапорев выч мат.pdf

Скачиваний:

1141

Добавлен:

26.03.2015

Размер:

8 Мб

Скачать

☆

<<< < Предыдущая 8 9 10 11 12 13 14 15 16 17 18 1920 / 3620 21 22 23 24 25 26 27 28 29 30 31 32 > Следующая >>>

n−1

∑ fi

= 0.407831.

i=1

1 = 0.511443.

∑ f

i−

0.5

0.6

0.7

0.8

0.9

1.0

i=1

Iпрямh

= h∑ f

i−

= 0.025572,

i=1

+ f

n−1

= 0.05(0.097562 + 0.407831)= 0.025270,

I трапh

= h

+ ∑ fi

i=1

n−1

0.05

(0.195124 + 2.045772 + 0.815662)= 0.025471.

+ fn + 4∑ f

+ 2∑ fi

Iпараб =

i=1

i−

i=1

Оценим теперь погрешность вычислений только по теореме 4.1:


f (x)=	cos(0.4x2 +1)		, f / (x)=	− 0.8x sin(0.4x2 +1)(2.3 + sin(1.5x + 0.3))			+
f (x)=	2.3 + sin(1.5x + 0.3)		, f / (x)=	(2.3 + sin(1.5x + 0.3))2			+
	2.3 + sin(1.5x + 0.3)			(2.3 + sin(1.5x + 0.3))2
	+	−1.5cos(0.4x2 +1)cos(1.5x			+ 0.3)	.
	+		(2.3 + sin(1.5x + 0.3))2			.
			(2.3 + sin(1.5x + 0.3))2

Вторая производная уже получается настолько громоздкой, что оценка погрешности становится затруднительной. Тем не менее можно провести грубую оценку сверху

f // (x)≤ 0.118 + 2.618x − 0.640x2 ≤ 2.000. Итак, I − Iпрямh , трап ≤	2	0.5 0.052	= 0.000104.
	24

Так оно и есть, поскольку значения интеграла, полученные по формулам прямоугольников и трапеций, отличаются в четвертом знаке после запятой.

Для приближенного вычисления определенных интегралов часто используют следующий прием. Подынтегральную функцию f (x) аппроксимируют на [a, b] функцией g(x),

интеграл от которой легко вычисляется и полагают ∫b f (x)dx ≈ ∫b g(x)dx. Еще чаще использует-

ся другой подход. Интеграл I

представляют в виде суммы интегралов по отрезкам [xi−1 , xi ].

На каждом таком отрезке

f (x) аппроксимируют некоторой легко интегрируемой функцией

и ∫ f (x)dx ≈ ∑

∫gi (x)dx.

i=1 x

i−1

сетка на отрезке [−1,1]. Аппроксимируем

f (x) на i -м элементар-

Пусть t0

, t1 ,..., tm -

ном

отрезке

[xi−1 , xi ]

интерполяционным

многочленом

Pm,i (x)

узлами

z(ji )

= x

t j hi

, j = 0,1,2,..., m.

Например,

можно воспользоваться многочленом Лагранжа

i−

x − zk(i )

(x)

= ∑m

f (z(i ))l (i )

(x), l

(i )

(x)

= ∏m

. Вычислим

(x)dx =

z(k ) − z(i )

x ∫

m,i

j=0

m, j

k =0

m,i

k ≠ j

i−1

116

x = x

+ thi ,

i−

(i )

(x)dx =

dx =

dt,

= hi

∑a j f

+ t j yhi

∫ ∑ f (z j

)lm, j

, где

xi−1

j=0

i−

x = xi−1

= xi , t =1.

, t = −1, x

1 m

n xi

∫

∏

t −tk

dt. Тогда I h ≈

∑

∫

(x)dx = ∑h

∑a

f x

(4.7.1)

m,i

−1k =0 t j −tk

i=1 xi−1

i=1

j=0

i−

k ≠ j

Формулы такого вида называются квадратурными формулами Ньютона - Котеса .

b	N
Итак, все квадратурные формулы имеют вид ∫ f (x)dx ≈ ∑Ai f (xi ), Ai - веса. Форму-
a	i=0

лы Гаусса строятся также по общему виду с дополнительным условием: формула должна быть точной для многочленов наиболее высокой степени. Как правило, формулы Гаусса сна-

(ti ), а затем с помощью замены

чала строятся для отрезка [−1,1], то есть ∫ f (x)dx ≈ ∑ai f

−1

i=0

x =

a + b

b − a

осуществляется переход к формулам интегрирования на произвольном

b − a

+ b

b − a

отрезке: ∫ f (x)dx ≈

∑ ai

ti .

i=0

Требование точности формулы для многочленов степени m эквивалентно требова-

нию ее точности для функции

f (t):1, t, t2 ,..., tm (базис для

(x)). Следовательно,

1 − (−

k +1

∑ai tik

= ∫tk dt =

, k = 0,1,..., m.

(4.8.1)

k +1

i=0

−1

Уравнение (4.8.1) дает систему нелинейных уравнений для определения ai

и ti . Этих

переменных a0 , a1 ,..., aN , t0 , t1 ,..., tN

штук. Следовательно, необходимый многочлен будет

иметь степень

m = 2N +1 , так как нужно учесть, что t0

= 1. Построим, например, квадра-

турную формулу Гаусса с двумя и тремя узлами.

i =1 - два

а). N =1,

m = 2N +1 = 3. Индекс i пробегает значения 0, N, то есть i = 0,

узла. По формуле (4.8.1) получим

k = 0, a0 + a1 = ∫1 1dt = 2,

−1

k =1,

a0t0 + a1t1 = ∫1 tdt = 0,

−1

k = 2, a0t02 + a1t12 = ∫1 t 2 dt = 2

−1

k = 3, a0t03 + a1t13 = ∫t3dt = 0.

−1

Итак, соответствующая нелинейная система уравнений имеет вид

Роджер Котес (1682-1716) - английский математик.

117

		a0				+ a1	= 2,
a				t	0	+ a t		= 0,					a0 = a1 = 1,
		0				1 1			2					1 , t		= 1 .
	a	t		2		+ a t	2	=		,	t	0	= −
				0											1
	0					a 1			3					3		3
a			t3			+ a t3
								= 0.
	0			0		a	1

Таким образом, получаем квадратурную формулу Гаусса:

																1									1		+				1														(4.8.2)
																∫ f	(t)dt ≈ f −										+	f					,												(4.8.2)
																−1									3						3
точную для многочленов третьей степени.
				б). N = 2,						m = 2N +1 = 5, i = 0,1, 2. Формула (4.8.1) дает
																													1
																	k = 0, a0 + a1 + a2 = ∫1dt = 2,
																													−1		1
																															1
																k = 1,			a0t0			+ a1t1 + a2t2 = ∫tdt = 0,
																																−1
																															1						2
																k = 2, a0t02 + a1t12 + a2t22 = ∫t																	2 dt =				2	,
																k = 2, a0t02 + a1t12 + a2t22 = ∫t																	2 dt =				3	,
																															−1						3
																															1
																k = 3, a0t03 + a1t13 + a2t23 = ∫t3dt = 0,
																																−1
																															1						2
																k = 4, a0t04 + a1t14 + a2t24 = ∫t																	4 dt =				2	,
																k = 4, a0t04 + a1t14 + a2t24 = ∫t																	4 dt =				5	,
																															−1						5
																															1
																k = 5, a0t05 + a1t15 + a2t25 = ∫t5dt = 0.
																															−1
Аналогично для нахождения переменных																								a j		и t j		будем иметь систему уравнений
		a0 + a1 + a2 = 2,
		a		0	t	0	+ a t	+ a				t		2	= 0,																										8
				0		0	1 1				2			2	= 2 ,													a0 = 0,					a1 = a2 = a3 =								8	,
		a		t	2		+ a t2	+ a				t		2	= 2 ,													a0 = 0,					a1 = a2 = a3 =								9	,
			0		0		1 1				2		2		3											1																	1
					3		3							3	3		t		= 0,			t		= −		1		= −0.774576,										t		= 0, t		=	1	= 0.774576.
		a0t0					+ a1t1	+ a2t2							= 0,			0				1				5													2		3		5
					4		4							4	2
					4		4							4	2
		a0t0					+ a1t1	+ a2t2							= 5 ,											3																	3
		a			t5		+ a t5	+ a					t5		= 0.
			0		0		1 1				2			2							являются корнями многочленов Лежандра P																									(t), а
Можно показать,											что значения							t	j		являются корнями многочленов Лежандра P																									(t), а
																			j																									N +1
							2								, где P (t)=1,						(t)= t, P (t)=								3					1
a		=																	P											t 2			−		и так далее.
a	j	=	(1	− t 2 )[P /					(t		)]2								P										2	t 2			−	3	и так далее.
	j		(1	− t 2 )[P /					(t	j	)]2					0			1							2			2					3
							j N +1			j
				Итак, квадратурная формула Гаусса в случае б) имеет вид

															1		8					1				8					8				1
															1	(t)dt ≈	8					1				8	f (0)+				8				1										(4.8.3)
															∫ f			f		−					+								f				.
															∫ f		9	f		−					+	9					9		f				.
															−		9					5				9					9				5
															1							5													5

																							3													3

Она точна до многочленов пятой степени. На таких же принципах могут быть построены квадратурные формулы Чебышева, Лагерра , Эрмита.

Для квадратурной формулы Гаусса справедлива следующая оценка погрешности:

Андриен Мари Лежандр (1752-1833) - французский математик.Эдмунд Николя Лагерр (1834-1886) - французский математик.

118


	R	≤ αN M 2 N +2 (b − a)2 N +3 ,
	R	≤ αN M 2 N +2 (b − a)2 N +3 ,
αN =			[(N +1)!]4		(4.8.4)
				.
			(2N + 3)[(2N + 2)!]3	.
Ее коэффициенты убывают очень быстро, например, α4					<10−13.

cos(ln(x))

sin(ln(x))

simplify → cos(ln(x)).

Численное дифференцирование применяется в тех случаях, когда либо невозможно, либо очень сложно или дорого продифференцировать функцию аналитически. Из-за быстрого накопления ошибок при численном вычислении старших производных обычно ограничиваются нахождением первой и второй производной по формулам (4.1.1), (4.1.2) и (4.1.5).

Одним из способов повышения точности вычислений является уменьшение шага до предела, определяемого выражением (4.4.1). Однако если функция задана на сетке, то при численном дифференцировании невозможно выбрать шаг h , меньший шага сетки, и тогда формулы (4.1.1)-(4.1.5) могут давать слишком большую погрешность. В этом случае исходную функцию часто аппроксимируют какой-либо гладкой функцией, значение производной от которой принимают за приближенное значение искомой производной.

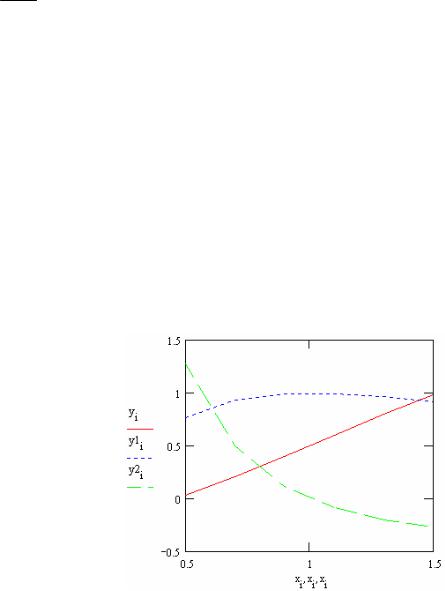
Пример. Пусть дана функция y = 2x (sin ln x + cos ln x). Найдем ее первую и вторую

производные, вычислим правую, левую и центральную первые разностные производные, вторую разностную производную по формуле (4.2.1) на отрезке x [0.5,1.5] и исследуем влияние шага h на точность вычислений.

Легко проверить, что y / = cos ln x, y // = − 1x sin ln x. Выберем первоначально h = 0.2.

Введем с клавиатуры исходные данные и построим графики y(x), y / (x) и y// (x):

ORIGIN := 1 f (x):= 2x (sin(ln(x))+ cos(ln(x))).

Первая и вторая производные этой функции уже найдены. Однако это можно было сделать в среде пакета Mathcad, причем двумя способами: с помощью панели инструментов Calculus (Панель операций математического анализа) и через меню символьных операций

Symbolics.

С помощью меню производная находится следующим образом. В рабочий документ надо ввести выражение дифференцируемой функции, выделить синим уголком аргумент (переменную дифференцирования) и щелкнуть по строке Differentiate в пункте Variable меню

Symbolics:

119

Ниже появится выражение для производной:

1	sin(ln(x))+	1	cos(ln(x))+	1	cos(ln(x))		−	sin(ln(x))
2		2		2	x	x		x	.

Выделяем все выражение и выбираем пункт Simplify в меню Symbolics. Ниже получим cos ln(x).

Вторая возможность связана с оператором символьных преобразований

и оператором символьных преобразований с ключевым словом панели ключевых слов символьных выражений. Набираем оператор . В квадратик вставляем опера-

тор dfdx(x) из панели Calculus. После щелчка вне этого оператора слева от него появляется

выражение для производной, которое можно упростить, выбрав оператор simplify в той же панели ключевых слов символьных выражений. В итоге получим следующее выражение:

df (x)	→	1	sin(ln(x))+	1	cos(ln(x))+	1	x
dx		2		2		2

Аналогичные действия нужно выполнить для нахождения второй производной, которая сразу получается в окончательном виде и более не упрощается оператором simplify.

Вводим с клавиатуры следующую информацию:

f 1(x):= cos(ln(x)) f 2(x):= −1		sin(ln(x))	a := 0.5 b :=1.5 h := 0.2 n :=	(b − a)
f 1(x):= cos(ln(x)) f 2(x):= −1		sin(ln(x))	a := 0.5 b :=1.5 h := 0.2 n :=	h
	x			h
i :=1...n +1 xi := a + h (i −1)	yi := f (xi )		y1i := f 1(xi ) y2i := f 2(xi ).

В точке x = a возможно вычисление только правой разностной производной по формуле (4.1.1), в точке x = b - только левой. Центральная разностная производная по формуле (4.1.5) не может быть посчитана при x = a и x = b . Вводим следующую часть программы:

i := 1...n

(yi+1

− yi )

n+1

:= 0

− yi−1 )

i := 2...n

(yi

:= 0

)

i+1

− y

i−1

i := 2...n yC

:= 0

n+1

:= 0

120

Наконец, находим вторую разностную производную по формуле (4.2.1). Она также не может быть посчитана в первой и последней точках заданной сетки узлов:

y2C := 0	y2C	n+1	:= 0 i := 2...n y2C	i	:=	(yi−1 − 2 yi + yi+1 )
						h2
1

Уменьшим теперь шаг, например, в четыре раза. Для построения графиков необходимо пересчитать все значения функции и производных во всех новых точках сетки. Скопируем всю программу вместе с графиками после оператора h := 0.005. Для этого надо, нажав левую мышку и не отпуская ее, обвести копируемую часть пунктирной линией. Затем щелкнуть по любому месту обведенной части правой мышкой. Появится дополнительное меню

Необходимо выбрать пункт копирования (Copy). Обведенная пунктирной линией часть программы скопируется в буфер обмена. Затем необходимо подвести курсор к нужному месту окна рабочего документа. Щелкнув в этом месте еще раз правой мышкой, раскроем то же дополнительное меню и выберем на этот раз пункт вставки (Paste). Копируемый кусок программы поместится ниже курсора. Приведем здесь лишь графики первых и вторых производных.

Видно, что точность представления производных заметно возросла. На первом графике первая центральная разностная производная, а на втором графике вторая разностная производная практически совпали с точными значениями, вычисленными по аналитическим выражениям:

121

Задание № 1. Для данных функций построить правую, левую и центральную первые разностные производные, вторую разностную производную на указанном интервале с данными шагами сетки h1 и h2 и сравнить полученные значения с точными значениями производных:

y = ln(x2

x 4

+1),

x [1, 2.5],

= 0.3,

= 0.05.

y = 2sinx 2 , x [0, 2], h = 0.4,

= 0.05.

y = sin cos2

x cos sin 2

x 0,

π ,

y = cos

x [1, 5],

= 0.5,

h2 = 0.05.

log 2

y =

arctg x2

−1,

x [1, 2],

= 0.2,

= 0.05.

1−x

y = e

, x [0,1],

= 0.2,

= 0.05.

1+x

y = ln ln ln x

2 ,

x [1,10],

= 2,

= 0.5.

y =

2x2

+1,

x [−1,1],

= 0.4,

h = 0.1.

y = e−

x [− 2, 2],

= 0.4,

= 0.1.

10.

y = arccos(sin x4

− cos x4 ),

π ,

= π ,

y = sin(arcsin x),

x [0,1],

11.

= 0.2,

= 0.05.

12.

y = 3arcctg(2 x+π),

− π

π ,

x [1,10],

13.

y = ln ln

=1,

= 0.25.

14.

y = 2cos2 x ,

x [0, 2],

= 0.4,

= 0.05.

15.

y = log3

(2x + 3)2 ,

x [1, 8],

= 0.5,

= 0.1.

x [−1,1],

16.

y = cos(3arccos x),

= 0.4,

h2 = 0.1.

17.

y =10

, x [1, 9],

=1,

= 0.2.

log3 x

122

18.

y = arcctg2x ,

x [1, 3],

h = 0.5,

= 0.1.

19.

y = cos

x [1, 4],

= 0.5, h

= 0.05.

20.

y = ln(x +

1 + x2 ),

x [0,1],

= 0.2,

= 0.05.

21.

y =

1 − x2

arcsin x,

x [−1,1],

h = 0.25, h

= 0.05.

22.

y = xe x2 , x [0,1],

= 0.1,

= 0.02.

x [1,10],

23.

y = x ln x,

=1,

= 0.25.

24.

y =

4 − x2 ,

x [0, 2],

h = 0.25,

= 0.05.

25.

y = arcsin x ,

x [− 0.9, 0.9],

= 0.2,

= 0.05.

1 − x2

26.

y = sin x ecos x , x

π , h =

27.

y = ln

1 − ex

x [−3,1],

= 0.25,

= 0.05.

1 −3x, x [− 2, 0],

28.

y = arccos

= 0.25,

= 0.05.

29.

y = ex (sin 3x −3cos 3x),

π ,

200

30.

y = arctg

x +1

, x [0, π], h

= π,

h =

x −1

В среде Mathcad возможно численное интегрирование заданных функций и символьное интегрирование. Символьное интегрирование можно выполнить двумя способами, так же как и дифференцирование: с помощью панели операций математического анализа и через меню символьных операций.

С помощью меню нужно выполнить аналогичные действия, что и при дифференцировании: ввести выражение интегрируемой функции, выделить аргумент и щелкнуть по строке

Integrate в пункте Variable меню Symbolics. В случае f (x) и f 1(x) получим 2x (sin(ln(x))+ cos(ln(x)))

201 x(2+i ) − 203 i x(2+i ) + 201 x(2−i ) − 203 i x(2−i ) cos(ln(x))

2x (sin(ln(x))+ cos(ln(x))).

Таким образом, только интеграл от f 1(x) имеет действительное аналитическое выражение, ∫ f (x)dx выражается в комплексном виде. Аналогичный результат получается при

использовании оператора символьных преобразований
∫ f (x)dx →	1	x(2+i )	−		3	i x(2+i ) +	1	x(2−i ) −	3	i x(2−i )
					20		20
20				1				20
∫ f 1(x)dx →					x (sin(ln(x))+ cos(ln(x))).
			2

Численное интегрирование также можно осуществить двумя путями: с помощью па-
нели операций математического анализа								и панели равенств и отношений			.
								123

В среде Mathcad знак = означает числовой, а знак → символьный вывод значения переменной, функции или выражения, записанного до этого знака. При численном интегрировании удобнее пользоваться оператором = . В нашем случае

1∫.5 f (x)dx → .50169909119550428276 −1. 10−21 i

0.5

1∫.5 f (x)dx = 0.5016991

0.5

1∫.5 f 1(x)dx → .95245452085281105139

0.5

1∫.5 f 1(x)dx = 0.9524545.

0.5

Формулы численного интегрирования (4.5.3), (4.5.4) и (4.5.6) настолько просты, что значение интеграла можно подсчитать, используя несколько арифметических операторов или с помощью небольшой подпрограммы. Например, формула центральных прямоугольников реализуется таким образом:

i :=1...n finti :=		h	n
i :=1...n finti :=	f xi +	2	I := h ∑fint j I = 0.5016835.
		2	j=1

Подпрограмма вычислений по формуле парабол (4.5.6) может быть такой:

I1:= parab(f , a,b, n) I1 = 0.5016991 I 2 := parab(f 1, a,b, n) I 2 = 0.9524545

Ее параметры: f - интегрируемая функция, которая должна быть ранее определена в программе, a, b - пределы интегрирования, n - число точек сетки (четное число для формулы парабол).

Задание № 2. Найти численное значение интеграла от функций, указанных в задании № 1, на заданном промежутке. При вычислении по подпрограмме parab выбрать n , соответствующее меньшему значению шага.

124

<<< < Предыдущая 8 9 10 11 12 13 14 15 16 17 18 1920 / 3620 21 22 23 24 25 26 27 28 29 30 31 32 > Следующая >>>

Соседние файлы в предмете Вычислительная математика

#
26.03.20151 Мб120Matlab.doc
#
26.03.20158 Мб1141шапорев выч мат.pdf