Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Балтийский государственный технический университет "ВОЕНМЕХ" им. Д.Ф. Устинова

Предмет:

Вычислительная математика

Файл:

шапорев выч мат.pdf

Скачиваний:

766

Добавлен:

26.03.2015

Размер:

8.33 Mб

Скачать

☆

<<< < Предыдущая 11 12 13 14 15 16 17 18 19 20 21 2223 / 3623 24 25 26 27 28 29 30 31 32 33 34 35 > Следующая >>>

	-0.15	-0.12	0.68	0.18	0.3400
	-0.25	-0.21	0.16	0.97	0.6300
	10.80	0.05	0.06	0.07	12.1430
24	0.03	9.90	0.05	0.06	13.0897
24	0.04	0.04	9.00	0.08	13.6744
	0.04	0.04	9.00	0.08	13.6744
	0.02	0.03	0.04	8.10	13.8972
	12.10	5.28	0.64	0.75	14.8310
25	0.37	11.20	5.86	0.69	15.9430
25	0.31	0.42	10.30	6.44	16.6926
	0.31	0.42	10.30	6.44	16.6926
	2.60	0.37	4.81	19.40	17.0800
	13.40	5.81	0.70	0.82	17.7828
26	0.41	12.50	6.50	0.77	19.0599
26	0.36	0.48	11.60	7.18	19.9744
	0.36	0.48	11.60	7.18	19.9744
	0.31	0.43	0.54	10.70	20.5261

№ вари-										Вектор
№ вари-				Матрица A						правой
анта				Матрица A						правой

										части b
										части b
		0.94		-0.18		-0.33		-0.16		2.4300

27		-0.32		1.00		-0.23		0.05		-1.1200

		-0.16		0.08		1.00		0.12		0.4300
		-0.16		0.08		1.00		0.12		0.4300

		-0.09		-0.22		0.13		1.00		0.8300
	1.00		-0.34		-0.23		0.06		1.4200

28		-0.11		1.23		0.18		-0.36		-0.6600

		-0.23		0.12		0.84		0.35		1.0800
		-0.23		0.12		0.84		0.35		1.0800

		-0.12		-0.12		0.47		0.82		1.7200
		0.68		0.23		-0.11		0.06		0.6700

29	-0.18		0.88		0.33		0.00		-0.8800

		-0.12		-0.32		1.05		-0.07		0.1800
		-0.12		-0.32		1.05		-0.07		0.1800

		-0.05		0.11		-0.09		1.12		1.4400
		0.77		0.14		-0.06		0.12		1.2100

30		-0.12		1.00		-0.32		0.18		-0.7200

		-0.08		0.12		0.77		-0.32		-0.5800
		-0.08		0.12		0.77		-0.32		-0.5800

		-0.25		-0.22		-0.14		1.00		1.5600

5.10. Постановка задачи нахождения собственных чисел

Вычисление собственных чисел и векторов матриц - одна из весьма сложных вычислительных задач. Рассмотрим несколько методов их нахождения.

Число λ называется собственным значением (собственным числом) матрицы A , если существует ненулевой вектор x , удовлетворяющий уравнению

				(5.10.1)
		Ax	= λ x.
		называется собственным вектором матрицы		A , соответствующим собственному
	x
числу λ.

Перепишем (5.10.1) в виде (A − λ E)x = 0. Это однородная система уравнений. Чтобы

существовало решение этой системы x ≠ 0 , необходимо чтобы определитель матрицы этой системы был равен нулю, то есть

	det(A − λ E) = 0.					(5.10.2)
Раскрытие этого уравнения приводит к характеристическому уравнению
λ n+ p λ n−1+ p		λ n−2+ ... + p	λ + p	n	= 0,	(5.10.3)
1	2		n−1	n
		141

представляющему собой алгебраическое уравнение степени n . Решение уравнения (5.10.3) дает все n собственных значений λ 1, λ 2,..., λ n квадратной матрицы An×n . Если матрица A

симметрическая, то все ее собственные значения - вещественные числа.

Классические численные методы решения проблемы собственных значений сводились, в конечном счете, к решению характеристического уравнения. Методы такого класса получили название прямых методов. Однако если размерность матрицы A будет составлять несколько десятков, а то и сотен единиц, такой подход становится неудовлетворительным. Для матриц высокого порядка возникает трудно разрешимая проблема вычисления коэффициентов характеристического уравнения с достаточной точностью.

Современные методы решения проблемы собственных значений основаны на совершенно иных идеях. Как правило, это итерационные алгоритмы, в которых собственные значения вычисляются как пределы некоторых числовых последовательностей без предварительного определения коэффициентов характеристического уравнения. Одновременно с нахождением собственных значений определяются и собственные векторы.

5.11. Подобные матрицы

Матрицы A и B называются подобными, если B = P−1 AP . При этом должна существовать невырожденная матрица подобия P .

Преобразование подобия есть результат перехода к новому базису в пространстве n -мерных векторов. Пусть y = Ax. Произведем замену переменных x = Px′, y = P y′. Тогда равенство y = Ax примет вид y′ = P−1 AP x′, то есть то же преобразование в новых переменных осуществляется не матрицей A , а подобной ей матрицей P−1 AP . Рассмотрим характеристическое уравнение матрицы P−1 AP :

det(P−1 AP − λ E)= det[P−1 (A − λ E)P]= det P−1 det(A − λ E)det P = det(A − λ E).

Таким образом, характеристические уравнения, а следовательно, и собственные числа мат-

риц	A и P−1 AP совпадают. Соответствующие собственные вектора																	не	совпадают, они
связаны равенством			= P
связаны равенством		x	= P	x′.
	Оказывается, существуют преобразования подобия, приводящие исходную матрицу
A к треугольному виду. Именно, справедлива
	Теорема 5.8. Любую квадратную матрицу A с помощью преобразования подобия
можно привести к следующему виду:
						λ	1	σ	1	0		0 ...			0	0
							1		1	σ2
						0		λ 2		σ2		0 ...			0	0
						0		0		λ		σ		...	0	0			(5.11.1)
	P−1 AP = Λ =										3		3			...	.		(5.11.1)
					... ... ... ... ... ...											...
						0		0		0		0 ...			λ n−1	σn−1
						0		0		0		0 ...			λ n−1	σn−1
						0		0		0		0 ...			0	λ n
						0		0		0		0 ...			0	λ n
Здесь	λ 1, λ 2,..., λ n - собственные числа матрицы A .														Если	λ i = λ i+1 ,		то	σi = 1, если же

λ i ≠ λ i+1 , то σi = 0 . Матрица (5.11.1) называется жордановой формой матрицы A .

5.12. Локализация собственных значений

Иногда удается получить грубые оценки расположения собственных чисел. Имеется

несколько локализационных теорем, одна из них - теорема Гершгорина. Пусть ri = ∑ aij -

j=1 j≠i

Мари Энмон Камиль Жордан (1838-1922) - французский математик.

142

сумма вне диагональных элементов i -й строки матрицы A . Обозначим через Si круг радиуса ri на комплексной плоскости с центром в точке aii ; круги Si называются кругами Герш-

горина.

Теорема 5.9. Все собственные значения матрицы A лежат в объединении кругов S1 , S2 ,..., Sn . Если какой-либо круг Гершгорина изолирован, то он содержит ровно одно

собственное значение матрицы A .

(A − λ E)

Действительно,

запишем

уравнение

= 0

скалярной

форме:

− λ xi

где xi

aii xi + ∑aij x j

= 0,

- максимальная по модулю координата вектора x .

i≠ j

(aii − λ )xi = −∑aij x j .

Так как

x j

≤1, то

aii

− λ

≤ ∑ aij

x j

≤ ri , то есть λ Si .

i≠ j

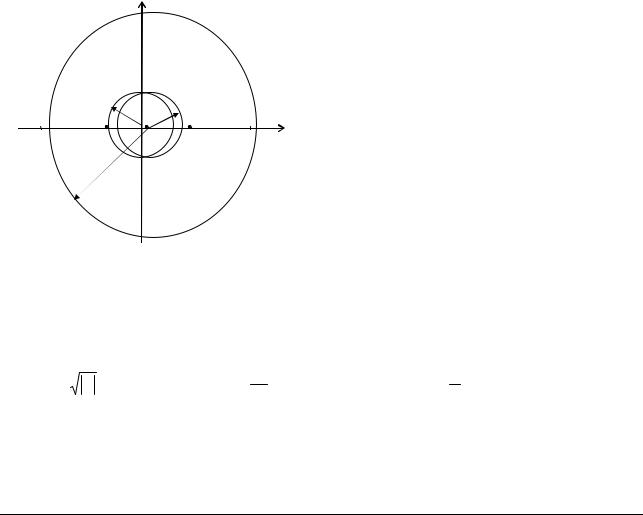
Пример. Найти все собственные числа матрицы

A и изобразить на плоскости круги

Гершгорина:

= 3,

=11,

r3 = 3.

A =

. Вычислим сначала радиусы кругов.

−1 0

= {z C :

≤ 11},

Итак,

= {z C :

z − 1

≤ 3},

S 2

z − 1

= {z C :

≤ 3}.

Очевидно,

S1 и S3 S2

и объединением всех кругов является S2 . Все собственные числа лежат внутри

круга S2 . Найдем λ 1, λ 2, λ 3 , решив характери-

стическое уравнение для данной матрицы A :

1 − λ

= 0 = λ 3− 2λ 2 −17λ +1. Для

1 − λ

−1

− λ

-10

решения

кубического

уравнения

применим

λ2

λ3

λ1

формулы

Кардано.

Уравнение

вида

ax3 + bx2

+ cx + d = 0

заменой

перемен-

ной

y = x +

приводится

виду

y3 + 3 py + 2q = 0 , где 2q =

2b3

−

27a3

3a2

-10

3p =

−

нашем

случае

3a2

Число

действительных

2q = −10.925925, q = −5.462963, 3 p = −18.333333,

p = −6.111111.

решений

уравнения y3 + 3py + 2q = 0

зависит

от

знака

дискриминанта

D = q2 + p3 .

D = −198.38 < 0. Если D < 0, то уравнение имеет три действительных различных корня, ко-

торые

находятся

следующим

образом.

Вычисляются

r = sgn q

= −2.4720661, cos ϕ =

= 0.361616, ϕ = 68o.8005,

ϕ = 22o.9335.

нахо-

r 3

дятся

сами

корни:

y1 = −2r cos

= 4.5533381,

y2 =

−

= −3.945106,

2r cos

Семен Аронович Гершгорин (1901 - 1933) - российский математик.Джироламо Кардано (1501-1576) - итальянский математик.

143

x2 = −3.278439,

= 2r cos

= −0.608232,

= y1 −

= y1 +

= 5.241808,

= 0.058435. Итак, λ 1= 5.242, λ 2 = −3.278, λ 3 = 0.058 с точностью ε = 10−3.

При вычислении собственных чисел и собственных векторов симметрических матриц

важную роль играет функция

)

ρ(x) =

(5.12.1)

(

)

которая называется отношением Релея.

Теорема 5.10. Пусть A - симметрическая матрица. Тогда

1) минимальное и максимальное собственное число матрицы A равны

λ min = min ρ(x),

λ max = max ρ(x);

(5.12.2)

x≠0

2) вектор

является стационарной точкой ρ(x), то есть gradρ(x)= 0

тогда и только тогда, когда

- собственный вектор матрицы A .

5.13. Степенной метод

Пусть необходимо вычислить максимальное по модулю собственное число λ, матри-

цы A , причем

λ 1

λ 2

> ... >

λ n

. В степенном методе используется следующая последо-

вательность формул. Выбирается произвольный начальный вектор

(0)

и строится последо-

вательность векторов {x

(k )}∞k =0 и приближений к собственному числу λ 1

{λ 1

(k )}∞k =0 таким об-

разом:

(k ) =

(k −1),

(k )

(k ), x(k −1) )

(5.13.1)

(k −1),

(k −1)

Правая часть формулы для λ 1(k ) в (5.13.1)

это отношение Релея при

(k −1).

(Ax

(k −1),

(k −1) )

(k )

(k −1)

(k )

(k −1)

= ρ (x

= Ax

, то λ 1

(k −1),

(k −1))

Теорема 5.11. Пусть в разложении

(0) = c

+ c

+ ... + c

n по базису

Так как

{ei }in=1 из

собственных векторов произвольной матрицы

A , собственные числа которой удовле-

творяют условию

> ... >

и c

≠ 0.

Тогда λ (k )→ λ

при k → ∞

и справед-

лива следующая оценка погрешности:

δ (λ 1(k ) )=

λ 1(

k )− λ 1

λ 2

≤ c

, c = const .

(5.13.2)

При практических вычислениях вектор x(k ) нормируют, чтобы не было переполнения или исчезновений порядка. Формулы (5.13.1) тогда приобретают вид

Джон Уильям Рэлей (1842 -1919) - английский физик и математик.

144

(k ) = Ax

(k −1),

(k )

(k −1)

λ (k )= (y

, x

(5.13.3)

(k )

(0)

(k )

=1.

В общем случае при решении проблемы собственных значений не существует эффективных апостериорных оценок погрешностей. Для симметрических матриц можно использовать следующий результат.

Теорема 5.12. Пусть λ

произвольное число,

- произвольный ненулевой

вектор. Тогда для любой симметрической матрицы A существует собственное число λ

такое, что справедлива оценка

− λ

λ − λ

≤

(5.13.4)

(k −1) -

В частности для степенного метода,

если

приближенно вычисленный собст-

венный вектор, а λ 1(k )- приближенное значение собственного числа, то

(k )

(k −1)

− λ

(k )

λ 1 − λ 1

≤

x(k −1)

(5.13.5)

(k )

(k −1)

= Ax .

Пример. Для матрицы из предыдущего примера вычислить λ 1

1 ,

взяв в качестве

начального приближения

(0) = (1,0,0)T .

(0)

(1)

(0)

Вычисления

будем

производить

по формулам

(5.13.3):

= Ax

1 2 1

(1)

(0)

(1)

9 1 2

λ 1

= (y

, x

(1 1 + 0 9 + 0 2) = 1, y

= 12 + 92 + 22 =

2 −1 0

(1)

0.107833

= 9.273618,

(1)

0.970495

Результаты вычислений шестнадцати итераций

(1)

0.215666

приведены в следующей таблице:

Номер итерации k

	λ (k )		x(k )		x2(k )	x3(k )
	1		1


	-		1.0000000		0.000000	0.000000

1		0.107833		0.970945		0.215666

	2.401193		0.670351		0.707602	-0.223450

	5.560346		0.282393		0.954482	0.096011

	4.128699		0.524958		0.846417	-0.089436

145

<<< < Предыдущая 11 12 13 14 15 16 17 18 19 20 21 2223 / 3623 24 25 26 27 28 29 30 31 32 33 34 35 > Следующая >>>

Соседние файлы в предмете Вычислительная математика

#
26.03.20151.18 Mб99Matlab.doc
#
26.03.20158.33 Mб766шапорев выч мат.pdf