
- •1. ЭЛЕМЕНТАРНАЯ ТЕОРИЯ ПОГРЕШНОСТЕЙ; ВЫЧИСЛИТЕЛЬНЫЕ ЗАДАЧИ, МЕТОДЫ И АЛГОРИТМЫ
- •1.1. Источники и классификация погрешностей результата численного эксперимента
- •1.2. Погрешности чисел
- •1.3. Погрешности арифметических операций
- •1.4. Погрешности функций
- •1.5. Особенности машинной арифметики
- •1.6. Лабораторная работа № 1. Определение абсолютной и относительной погрешностей приближенных чисел. Оценка погрешностей результата
- •1.7. Корректность вычислительной задачи
- •1.8. Обусловленность вычислительной задачи
- •1.9. Вычислительные методы, их классификация
- •2. ПРИБЛИЖЕНИЕ ФУНКЦИЙ
- •2.1. Задача приближения функций
- •2.2. Интерполяция обобщенными многочленами
- •2.3. Полиномиальная интерполяция. Многочлен Лагранжа
- •2.4. Погрешность интерполяции
- •2.5. Конечные разности и их свойства
- •Доказательство
- •2.6. Разделенные разности и их свойства
- •2.9. Лабораторная работа № 2. Интерполирование и экстраполирование данных. Интерполяционный многочлен Лагранжа
- •2.10. Интерполяционный многочлен Ньютона с конечными разностями
- •2.11. Лабораторная работа № 3. Интерполирование и экстраполирование данных. Интерполяционный многочлен Ньютона
- •2.12. Интерполяционные формулы Гаусса, Стирлинга и Бесселя
- •3. МЕТОД НАИМЕНЬШИХ КВАДРАТОВ И СПЕЦИАЛЬНЫЕ ИНТЕРПОЛЯЦИОННЫЕ МНОГОЧЛЕНЫ
- •3.1. Постановка задачи и вывод формул метода наименьших квадратов
- •3.3. Глобальная полиномиальная интерполяция
- •3.4. Чувствительность интерполяционного многочлена к погрешностям входных данных
- •3.5. Многочлены Чебышева
- •3.6. Решение задачи минимизации оценки погрешности
- •3.8. Лабораторная работа №5. Экономизация степенных рядов
- •3.9. Локальная интерполяция
- •3.10. Сплайны, их свойства и построение
- •3.11. Погрешность приближения кубическими сплайнами
- •3.13. Тригонометрическая интерполяция. Дискретное преобразование Фурье и его реализация на ЭВМ
- •3.14. Матричная форма записи дискретного преобразования Фурье (ДПФ)
- •3.15. Алгоритм реализации ДПФ
- •3.16. Пример реализации алгоритма ДПФ при
- •3.17. Лабораторная работа № 7. Дискретное преобразование Фурье
- •4. ЧИСЛЕННОЕ ДИФФЕРЕНЦИРОВАНИЕ И ЧИСЛЕННОЕ ИНТЕГРИРОВАНИЕ
- •4.1. Простейшие формулы численного дифференцирования для первой производной
- •4.2. Формулы численного дифференцирования для второй производной
- •4.3. Формулы численного дифференцирования, основанные на интерполяции алгебраическими многочленами
- •4.4. Обусловленность формул численного дифференцирования
- •4.5. Простейшие квадратурные методы численного интегрирования
- •4.6. Оценка погрешностей простейших квадратурных формул
- •4.7. Квадратурные формулы интерполяционного типа
- •4.8. Квадратурные формулы Гаусса
- •4.9. Лабораторная работа № 8. Численное дифференцирование и численное интегрирование функций
- •5. РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ И ПРОБЛЕМЫ СОБСТВЕННЫХ ЗНАЧЕНИЙ
- •5.1. Нормы векторов и матриц и их свойства
- •5.2. Обусловленность задачи решения системы линейных алгебраических уравнений
- •5.3. Метод Гаусса (схема единственного деления)
- •5.4. Метод прогонки
- •5.5. Метод простых итераций
- •5.6. Сходимость метода простых итераций
- •5.10. Постановка задачи нахождения собственных чисел
- •5.11. Подобные матрицы
- •5.12. Локализация собственных значений
- •5.13. Степенной метод
- •5.14. Вычисление собственных векторов методом обратных итераций
- •6. ЧИСЛЕННЫЕ МЕТОДЫ РЕШЕНИЯ НЕЛИНЕЙНЫХ УРАВНЕНИЙ И СИСТЕМ
- •6.1. Решение нелинейных уравнений
- •6.2. Метод Ньютона для уравнений
- •6.3. Сходимость метода Ньютона и трудности его применения
- •6.4. Метод Ньютона решения систем нелинейных уравнений
- •6.6. Модификации метода Ньютона
- •6.7. Лабораторная работа № 11. Решение систем нелинейных уравнений методом Ньютона
- •7. ЧИСЛЕННЫЕ МЕТОДЫ РЕШЕНИЯ ЗАДАЧИ КОШИ ДЛЯ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ И СИСТЕМ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
- •7.1. Задача Коши для дифференциального уравнения первого порядка
- •7.2. Численные методы решения задачи Коши. Основные понятия и определения
- •7.3. Решение с помощью рядов Тейлора
- •7.5. Анализ ошибок, возникающих при использовании методов Рунге - Кутты
- •7.6. Методы прогноза и коррекции
- •7.7. Сравнение методов
- •7.8. Лабораторная работа № 12. Методы интегрирования обыкновенных дифференциальных уравнений
- •7.9. Решение задачи Коши для систем обыкновенных дифференциальных уравнений
- •7.11. Лабораторная работа № 13. Численное интегрирование систем дифференциальных уравнений первого порядка
- •8. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ (УРАВНЕНИЯ МАТЕМАТИЧЕСКОЙ ФИЗИКИ)
- •8.1. Классификация уравнений математической физики
- •8.2. Простейшие задачи, приводящие к дифференциальным уравнениям в частных производных
- •8.4. Уравнения параболического типа. Явные и неявные схемы
- •Доказательство
- •8.5. Уравнения гиперболического типа
- •8.6. Уравнения эллиптического типа
- •8.7. Свойства разностных схем для дифференциальных уравнений: способность аппроксимировать исходную дифференциальную задачу, устойчивость и сходимость
- •8.8. Некоторые обобщения
- •8.9. Лабораторная работа № 14. Решение задачи Дирихле для уравнения Лапласа методом сеток
- •8.10. Лабораторная работа № 15. Решение однородного уравнения колебаний струны методом сеток по неявной схеме.
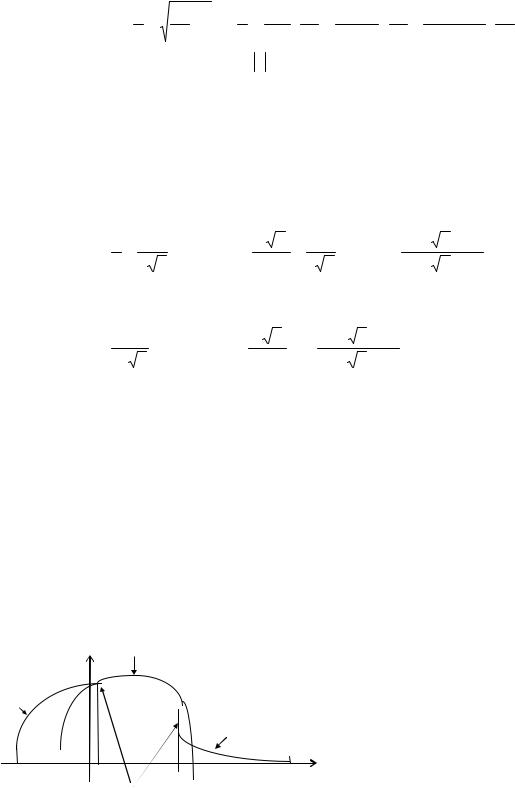
|
|
(x)= |
|
|
|
|
|
|
x 2 |
|
|
|
|
∞ |
|
|
|
|
(k!)2 |
|
|
|
|
|
2k |
+2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
21. |
f |
|
|
|
|
= |
∑ |
|
|
|
x |
|
|
|
x |
≤ 2, ε =10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
2 arcsin |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
k =0 (2k |
+ 2)! |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
22. |
f |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+1)! x2k +3 , |
|
x ≤ 2, ε = 2 10−3. |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
(x)= 2x − 2(4 − x2 )2 |
arcsin |
|
|
x = ∑ k!(k |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− x2 |
|
|
|
|
|
|
|
2 |
|
|
k =0 |
(2k + 3)! |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
23. |
|
( |
|
)= |
( |
+ |
|
) |
= |
|
|
|
|
+ x3 − x4 |
+ |
|
|
|
|
+ |
∞ |
|
(− |
|
)k +1 |
|
x k |
+ |
|
|
|
|
|
− |
|
|
|
< |
|
|
≤ |
|
ε = |
|
|
|
−3 |
|
||||||||||||||||||||||||||||||||||||||||||
|
f |
|
x |
|
ln 1 |
|
x |
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
... |
|
|
∑ |
|
|
|
1 |
|
|
|
|
|
|
|
|
..., |
|
|
|
1 |
|
x |
|
1, |
|
|
3 |
|
10 |
|
. |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
3 |
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k =1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
f |
|
|
|
|
|
|
|
|
|
|
|
x |
2 |
|
|
|
|
|
|
= |
|
x |
|
− |
|
|
|
1 |
|
|
|
|
|
x |
3 |
+ |
|
|
|
1 3 |
|
|
|
x |
5 |
− |
|
1 3 5 |
|
|
x |
7 |
+ ..., |
|
|
|
|
||||||||||||||||||||||||||||||||
|
(x)= ln x + |
|
|
|
|
|
+1 |
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
5 |
|
|
7 |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
24. |
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
2 3 |
|
|
|
2 |
|
|
|
|
2 4 5 |
2 |
|
2 |
4 6 7 |
|
2 |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x < 2, ε = 10−3. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
25. |
f |
(x)= ln cos x = − |
x2 |
|
− |
x4 |
|
− |
x6 |
− |
17 x8 |
|
− |
|
511x10 |
+ ..., |
|
x |
|
< |
|
π |
, ε = 10−3. |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
12 |
|
|
|
45 |
|
|
2520 |
|
|
|
467775 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
26. |
f |
(x)= |
|
1 |
[6x + 3x 2 |
+ 2x3 + 6(1 − x3 )ln(1 − x)]= ∑∞ |
|
|
|
x k +3 |
|
|
|
|
|
, |
|
x |
|
≤ 1, ε = 10 −3. |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
18 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(−1)k x2k +2 |
k =1 k(k + |
3) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
27. |
f (x)= −2x arctg x + ln(1 + x2 )= ∑∞ |
|
|
|
|
|
, |
|
|
x |
|
≤1, ε = 2 10−3. |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k =0 (k +1)(2k +1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
(x)= x + |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
1 + x |
2 + x2 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
f |
|
1 |
|
|
|
(x2 |
−1)arctg |
|
|
|
|
2 |
|
|
|
− |
|
|
1 |
|
|
(x2 |
|
+1)ln |
|
= |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
28. |
|
|
|
|
2 |
|
|
4 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 − x2 |
|
|
|
8 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 − x 2 + x2 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∞ |
|
|
|
|
(−1)k x4k +5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
= ∑ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
x |
≤1, ε =10−3. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
(4k + 3)(4k + 5) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k =0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(−1)k x4k +7 |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
(x)= |
1 |
|
(x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x 2 |
|
|
|
|
|
|
|
|
|
|
1 + x 2 + x2 |
|
|
∞ |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
f |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
− ln |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
= |
|
∑ |
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
4 |
−1) 2 arctg |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
29. |
|
|
|
|
16 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 − x |
|
|
|
|
|
|
|
|
|
|
|
1 − x |
2 + x |
|
|
|
|
|
k =0 (4k + 3)(4k + 7) |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
≤1, |
ε =10−3. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
30. |
f |
(x)= |
|
1 |
(sh x − sin x) |
= ∑∞ |
|
|
|
x 4k +3 |
|
|
|
|
|
, |
|
|
x |
|
< ∞, ε = 10 −4. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k =0 (4k + 3)! |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
3.9. Локальная интерполяция
Как было показано ранее, глобальная полиномиальная интерполяция не всегда приводит к желательному заявленному результату по ряду причин. Альтернативный подход состоит в локальной интерполяции, когда функция y = f (x) аппроксимируется интерполяцион-
ным многочленом Pm (x) малой степени m на [α, β] [a, b]. При этом, конечно, используется лишь часть табличных данных.
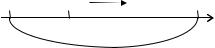
Самый простой подход при локальной интерполяции состоит в построении набора |
|||
полиномов |
P(0,1,..., m), P(1,2,...,m +1),..., P(n − m, n − m +1,...,n) фиксированной степени m , |
||
|
P2 |
|
каждый из которых совпадает с табличны- |
|
|
|
ми значениями в m +1 последовательной |
P1 |
|
|
точке. Каждый такой полином использует- |
|
|
P3 |
ся для интерполяции тех x [a, b], для ко- |
|
|
торых выбранные узлы таблицы являются |
|
|
|
|
|
|
|
|
ближайшими. Ясно, что в этом случае |
а |
разрывы I рода |
b |
имеются разрывы I рода интерполирован- |
|
|
ной функции в местах стыка многочленов |
|
|
|
|
|
83

Pi . Этот метод называется интерполяцией с помощью «движущегося» полинома.
|
|
|
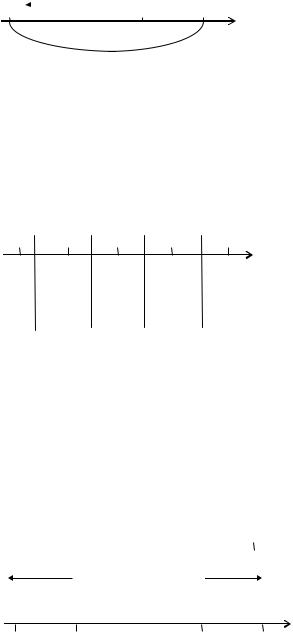
Другой подход состоит в кусочно-поли- |
|
|
|
номиальной интерполяции. В этом случае ис- |
P1 |
P2 |
P3 |
ходный отрезок [a, b] разбивается на несколько |
отрезков меньшей длины, на каждом из которых |
|||
|
|
|
y = f (x) интерполируется своим многочленом. |
|
|
|
При этом аппроксимируемая функция будет не- |
a |
|
b |
прерывной, но будет иметь точки излома, то есть |
|
|
|
не будет непрерывно дифференцируемой. |
3.10.Сплайны, их свойства и построение
В1946 году были созданы сплайн-функции, являющиеся по сути дальнейшим развитием метода кусочно-полиномиальной интерполяции. Пусть отрезок [a, b] разбит точками
x0 = a < x1 < ... < xn−1 < xn = b на n частичных отрезков [xi−1, xi ]. |
|
|
Сплайном степени m называется функция Sm (x), |
удовлетворяющая следую- |
|
щим свойствам: |
непрерывна на [a, b] вместе со |
|
1) Sm (x) |
всеми производными |
|
Sm(1)(x), Sm(2)(x),..., Sm(p)(x) до некоторого порядка p ; |
|
|
2) на каждом отрезке [xi−1 , xi ] [a, b] Sm (x) совпадает с некоторым алгебраиче- |
||
ским многочленом |
Pm,i (x) степени m . |
|
Разность m − p между степенью сплайна и порядком старшей производной, непрерывной на [a, b], называется дефектом сплайна.
Интерполяция ломаными-простейший случай сплайна-сплайна первой степени дефекта единица, где сама функция непрерывна, а уже первая производная разрывна. Наиболее широкое применение на практике получили сплайны S3 (x) - кубические сплайны с дефек-
том, равным единице или двойке. Такие сплайны на каждом из частичных отрезков [xi−1 , xi ]
совпадают |
с |
кубическим многочленом S |
3 |
(x) = P |
(x) = a |
i |
+ b |
(x − x |
)+ c |
(x − x |
i−1 |
)2 + |
||||||||||||||||||
+ di (x − xi−1 )3 и имеют на отрезке [a, b] |
|
|
|
|
3,i |
|
|
|
|
|
i |
|
i−1 |
i |
|
|
||||||||||||||
по крайней мере одну непрерывную производную |
||||||||||||||||||||||||||||||
S3/ (x). |
а). Интерполяционный сплайн. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
Пусть на концах отрезка [x |
0 |
, x ] |
заданы значения |
y |
0 |
, y , y |
/ и y/ |
. Тогда интерполяци- |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
P3 (x) , |
1 |
|
|
|
|
|
|
|
|
|
1 |
|
0 |
|
1 |
P3 (x0 ) = y0 , P3 (x1 ) = |
||||||
онный |
|
|
многочлен |
|
|
|
удовлетворяющий |
условиям |
|
|||||||||||||||||||||
= y , P / (x |
0 |
) = y / |
, P / (x ) = y / , может быть представлен в следующем виде: |
|
|
|
|
|||||||||||||||||||||||
1 |
3 |
0 |
|
3 |
1 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P |
(x)= y |
0 |
(x1 − x)2 (2(x − x0 )+ h) |
+ y/ |
(x1 − x)2 (x − x0 ) |
+ |
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
3 |
|
|
|
h3 |
|
|
|
|
0 |
|
h2 |
|
|
|
|
|
|
|
(3.10.1) |
|||||||
|
|
|
|
|
(x − x0 )2 (2(x1 − x)+ h) |
|
|
(x − x0 )2 (x − x1 ) |
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
+ y |
|
+ y/ |
, h = x − x |
. |
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
1 |
|
|
|
h3 |
|
|
|
1 |
|
|
|
h2 |
|
|
|
|
1 |
|
0 |
|
|
|
|
|
||
Эта формула проверяется непосредственно подстановкой граничных условий. Многочлен (3.10.1) называется кубическим интерполяционным многочленом Эрмита .
Сплайн Sm (x) называется интерполяционным, если Sm (xi )= yi для всех i = 0, n. Если определять этот сплайн на [xi−1, xi ], то необходимо задать yi−1 , yi , si−1, si , где si = Sm/ (xi ). Тогда по формуле (3.10.1) S3 (x)= P3,i (x).
Шарль Эрмит (1822-1901) - французский математик.
84
б). Глобальный сплайн.
Для того, чтобы на всем отрезке [a, b] сплайн имел непрерывную p -ю производную, в узлах сопряжения необходимо обеспечить условия касания p -го порядка, то есть
f (xi )= Pm (xi ), f / (xi )= Pm/ (xi ),
..........................
f (p )(xi )= Pm(p )(xi ).
Для кубического сплайна необходимо позаботиться о первой и второй производной в узлах сопряжения.
Сплайн-функции математически моделируют очень старое механическое устройство: гибкие рейки представляют собой механический сплайн. Если их жестко закрепить в узлах интерполяции, то рейки принимают форму, минимизирующую их потенциальную энергию, пропорциональную интегралу по длине дуги от квадрата кривизны рейки. Итак, если
S(x)-сплайн-функция, то |
x∫n [S // (x)]2 dx min. С математической точки зрения доказано, что |
|
x1 |
сплайн - это единственная функция, обладающая свойством минимальной кривизны среди всех функций, интерполирующих данные точки, то есть это самая гладкая из функций, применяемых для данной интерполяции. Из определения сплайна и определения касания p -го
порядка ясно, что если xi −i -й узел, то |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
Sm |
(xi − 0)= Sm |
(xi + 0), |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
Sm/ |
(xi − 0)= Sm/ |
(xi + 0), |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
..................................... |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
Sm(p )(xi − 0)= Sm(p )(xi + 0). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
Рассмотрим весь отрезок [a, b]. Построим на нем систему сплайнов |
S3 (x) с узлами |
|||||||||||||||||||||||||||||||||||||||||||||
сопряжения a = x0 |
< x1 < x2 < ... < xn−1 < xn |
= b с непрерывной второй производной. Для это- |
|||||||||||||||||||||||||||||||||||||||||||||
го необходимо выбирать наклоны s |
i |
= S / |
(x) |
|
так, чтобы в точках x |
i |
«стыка» многочленов P |
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3,i |
||||
и P3,i+1 |
совпали значения их вторых производных: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
P// |
(x |
|
)= P |
// |
|
(x |
), i =1,2,..., n −1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
3,i |
|
i |
|
|
|
3,i+1 |
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
Продифференцируем формулу (3.10.1) и найдем вторую производную, переписав эту |
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
формулу для |
|
|
узлов |
xi−1 |
и xi |
|
и |
вводя обозначения |
||||||||||||||||||||||||||||
xi-1 |
|
|
x |
|
cлева |
xi |
|
|
|
si = S3/,i (xi ): |
|
|
|
|
|
(x − xi )2 (2(x − xi−1 )+ hi ) |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S |
3 |
(x)= P |
|
(x)= |
y |
i−1 |
+ |
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
hi |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3,i |
|
|
|
|
|
|
|
|
h3 |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(x − xi−1 )2 (2(xi − x)+ hi ) |
|
i |
|
(x − xi )2 (x − xi−1 ) |
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ |
|
y |
i |
+ |
s |
i−1 |
+ |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
h3 |
|
|
|
|
|
|
|
|
|
|
h2 |
|
|
|
|
|
|
|
|||
|
|
(x − xi−1 )2 (x − xi ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
||||
|
+ |
s |
, h = x |
i |
− x |
i−1 |
. |
|
Отсюда |
|
S |
/ |
(x)= P/ |
|
(x) |
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
h2 |
|
i |
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
3,i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2(x − x |
)(2(x − x |
i−1 |
)+ h ) |
+ 2(x − x |
)2 |
|
yi−1 + |
|
2(x − x |
i−1 |
)(2(x |
i |
− x) |
+ h )− |
2(x − x |
i |
−1 |
)2 |
|
yi + |
||||||||||||||||||||||||
|
= |
|
i |
|
|
i |
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|||||||||||
|
|
|
|
|
h3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
h3 |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
+ |
2(x − xi )(x − xi−1 )+ (x − xi )2 |
|
si−1 + |
|
2(x |
|
− xi−1 )(x − xi )+ (x − xi−1 )2 |
si . |
Аналогично |
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
h2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
h2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
85
|
|
|
|
S // (x) |
= P// (x)= |
2(2(x − xi−1 )+ hi )+ 8(x − xi ) |
y |
i−1 |
+ |
2(2(xi − x)+ hi )− 8(x − xi−1 ) |
y |
i |
|
+ |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
3 |
|
|
|
|
|
3,i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
h |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
h3 |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
+ |
|
2(x − xi−1 )+ 4(x − xi ) |
s |
i |
−1 |
+ |
2(x − xi )+ 4(x − xi−1 ) |
s |
. |
|
Положим |
x = x |
, |
|
|
|
|
получим |
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
h2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
h2 |
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
4(xi − xi−1 )+ 2hi |
i |
|
|
|
|
|
|
2hi − 8(xi − xi−1 ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
S // (x |
i |
− 0)= |
P// |
(x |
)= |
y |
i−1 |
+ |
y |
i |
+ |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
3 |
|
|
|
|
|
|
|
3,i |
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
h3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
h3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ |
2(xi − xi−1 ) |
s |
i |
−1 |
+ |
4(xi − xi−1 ) |
s |
i |
= |
2si−1 |
+ |
|
4si |
|
− 6 |
|
yi − yi−1 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
h |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
h2 |
|
|
|
|
|
|
|
|
|
|
|
h2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
h |
|
|
|
|
|
|
h2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
xi |
|
|
|
|
|
|
|
справа |
|
|
|
x |
|
|
|
|
xi+1 |
|
|
|
|
|
|
|
|
|
Аналогично получается вторая производная справа. |
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Перепишем |
|
|
|
P |
// (x) |
|
для |
|
узлов |
x |
, x |
i+1 |
, |
заме- |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3,i |
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
hi+1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
няя |
|
xi на |
xi+1 и xi−1 |
|
на xi . |
Полагая |
затем |
x = xi , |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
в |
|
|
|
|
полученной |
|
|
формуле |
будем |
|
|
|
|
иметь |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
S // (x |
i |
+ 0) |
= |
P// |
|
(x |
) |
= − |
|
4si |
|
− |
|
2si+1 |
+ |
6 |
yi+1 |
− yi |
. Таким образом, |
|
записывая условия сопря- |
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
h |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
3 |
|
|
|
|
|
|
|
|
3,i+1 |
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
h |
|
|
|
|
|
|
|
|
h2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i+1 |
|
|
|
|
|
i+1 |
|
|
|
|
|
i+1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
жения второй производной во всех узлах промежутка [a, b], получим следующую систему |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
уравнений: |
|
+ 2(h |
−1 + h−1 )s |
|
|
|
|
|
|
|
|
|
|
|
|
= 3[h |
|
(y |
|
|
|
|
|
|
|
)+ h−2 (y |
|
|
|
|
|
)], i = 1,2,..., n −1. |
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
h−1s |
i−1 |
i |
+ h−1 s |
i+1 |
−2 |
i |
− y |
i−1 |
i+1 |
− y |
|
|
(3.10.2) |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
i |
|
|
|
i |
|
|
|
|
i+1 |
|
|
|
|
i+1 |
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
i+1 |
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
Неизвестными |
в |
этой |
|
системе |
служат |
|
si−1 , si , si+1. |
|
|
Число |
неизвестных |
n +1, |
|
|
а |
число |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
уравнений |
n −1. |
Таким образом, не хватает еще |
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
двух условий. Их выбор обычно связывают с неко- |
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
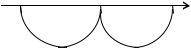
|
x1 |
|
|
|
|
x2 |
|
|
x3 |
|
|
|
|
|
|
x4 |
|
|
|
|
|
x5 |
|
|
|
|
торыми дополнительными |
условиями, |
|
|
наклады- |
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ваемыми на сплайн в граничных |
точках |
a и b |
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
s1, s 2, s3 |
s2, s3, s4 |
s3, s4, s5 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(граничные условия). Эти условия могут быть, на- |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
пример, таковы. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1. Если |
в |
|
граничных |
точках |
|
|
известны |
||||||||||||||||||
значения |
|
|
первой |
|
|
производной |
|
|
f / (a) |
|
|
и |
|
|
f / (b), |
|
то |
|
естественно |
|
положить |
|||||||||||||||||||||||||||||||||||||||||||||||||||
s0 |
= f / (a), |
|
sn = f / (b). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(3.10.3) |
|||||||||||||
Дополняя систему (3.10.2) уравнениями (3.10.3), приходим к системе уравнений с трехдиагональной матрицей, которая легко решается методом прогонки. Полученный таким образом сплайн называется фундаментальным кубическим сплайном.
2. Если в граничных точках известны f // (a) и f // (b), то S3// (a)= P3,1// (x0 )= f // (a) и S3// (b)= P3,//n (xn )= f // (b). Это дает следующие уравнения:
а) слева P// |
(x |
)= |
2si−1 |
+ |
4si |
− 6 |
yi − yi−1 |
, |
i = n , тогда P// |
(x |
n |
)= |
|
f // (b)= |
|
2sn−1 |
+ |
|
|
|
|||||||||||||||
h |
h |
h2 |
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
3,i |
i |
|
|
|
|
|
|
|
|
|
|
|
3,n |
|
|
|
|
|
|
|
|
h |
|
|
|
|||||||||
|
|
|
|
i |
|
i |
|
i |
|
|
4sn |
|
|
|
|
|
yn − yn−1 |
|
|
|
|
|
|
|
n |
|
|
|
|||||||
|
справа |
|
слева |
|
|
|
+ |
|
|
− 6 |
|
|
, б) справа P// |
(x |
)= |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
hn |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
3,i+1 |
i |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
hn |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
P3//,i+1 (xi |
), i = 0 |
|
|
P3//,i (xi ), i = n |
|
= − |
4si |
− |
|
2si+1 |
|
+ 6 |
|
yi+1 − yi |
, i = 0, |
тогда |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
h |
|
|
|
h |
|
|
|
|
|
h2 |
|
|
|
|
|
|
|
|
|
||||
a = x0 |
x1 |
… |
|
xn−1 |
xn = b |
|
|
|
|
i+1 |
|
|
|
i+1 |
|
|
|
|
|
i+1 |
|
|
|
|
|
|
|
|
|
||||||
|
|
P// (x |
0 |
) |
= |
|
f // (a)= − |
4s0 |
− |
2s1 |
+ 6 |
y1 − y0 |
. |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
3,1 |
|
|
|
|
|
|
|
|
|
|
|
h |
h |
h2 |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
1 |
|
|
|
1 |
|
|
||||
3. Можно положить |
f // (a)= 0, f // (b)= 0, тогда соответствующая система уравнений |
||||||||||||||||||||||||||||||||||
определяет так называемый естественный кубический сплайн. Благодаря большой простоте записи они получили широкое распространение, однако условие f // (a)= 0, f // (b)= 0 приводит к потере точности и, таким образом, естественный сплайн обладает лишь вторым поряд-
86
ком точности, в то время как все кубические сплайны имеют четвертый порядок точности относительно шага сетки узлов сопряжения, то есть O(h4 ).
4. Если нет никакой информации о значениях производных на концах отрезка, то прибегают к условию «отсутствие узла». Используются равенства P3,1 (x)≡ P3,2 (x) и
P |
(x)≡ P |
(x), для чего необходимо, чтобы |
P(3)(x )= P(3)(x ) |
P(3) |
(x |
n−1 |
)= P(3)(x |
n−1 |
). |
|
3,n−1 |
3,n |
|
3,1 1 |
3,2 1 |
3,n−1 |
|
3,n |
|
||
Выведем необходимые формулы: P/// |
(x)= |
|
4 + 8 |
y |
i−1 |
+ |
− 4 − 8 y |
i |
+ |
6 |
s |
i−1 |
+ |
6 |
s |
i |
||||||||||||||||||||||||||
|
|
|
|
h2 |
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3,i |
|
|
h3 |
|
|
|
|
h3 |
|
|
h2 |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
i |
|
|
|
i |
|
|
|
i |
|
|
= |
12 |
y |
i−1 |
− |
12 |
y |
i |
+ |
6 |
|
s |
i−1 |
+ |
6 |
s |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
h3 |
h3 |
h2 |
|
h2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
i |
|
|
|
i |
|
|
|
i |
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а). Cлева (x = x |
) |
P/// |
(x |
) |
= |
12 |
|
y |
0 |
− |
12 |
y + |
6 |
s |
0 |
+ |
6 |
|
s . |
|
x |
|
|
h |
|
x |
|
|
||||||||||||||
3 |
|
|
3 |
2 |
|
2 |
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
1 |
|
3,1 |
|
1 |
|
|
|
|
1 |
|
|
|
1 |
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
h1 |
|
|
|
|
h1 |
|
h1 |
|
|
|
|
h1 |
|
|
|
|
|
0 |
|
1 |
|
1 |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
=
h2 x2
б). Cправа |
(x = x ) |
P/// (x |
) |
= |
12 |
|
y |
|
− |
12 |
|
|
y |
|
+ |
|
|
6 |
|
s |
|
+ |
6 |
|
|
s |
|
. |
Так |
|
как |
|
|
P(3) |
(x )= P(3) |
(x ), |
то |
||||||||||||||||||||||||||||||||||||||||
|
h23 |
|
|
h23 |
|
|
|
|
h22 |
|
|
|
h22 |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
2 y0 |
|
|
|
|
s0 |
|
1 |
|
|
3,2 |
|
1 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
2 |
|
|
|
1 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
3,1 |
1 |
3,2 |
|
|
1 |
|
|
|
|||||||||||||||||||||||
|
− |
2 y1 |
|
+ |
+ |
s1 |
|
|
= |
2 y1 |
|
− |
2 y2 |
|
+ |
|
s1 |
|
+ |
s2 |
|
. |
Отсюда |
|
получим |
|
2h−3 (y |
|
− y ) |
+ h−2 (s |
|
|
+ s ) = |
||||||||||||||||||||||||||||||||||||||||||||
|
|
h3 |
|
h2 |
|
|
h2 |
h2 |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
h3 |
|
h |
2 |
|
|
h |
3 |
|
|
|
|
h3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
0 |
|
|
1 |
|
1 |
|
0 |
|
|
1 |
|
|
||||||||||||||||||
1 |
|
1 |
|
|
|
1 |
|
1 |
|
|
|
|
2 |
|
|
). |
2 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
= 2h−3 |
(y − y |
2 |
)+ h−2 |
(s + s |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
2 |
1 |
|
|
|
|
|
2 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Такие же преобразования для узлов xn−2 , xn−1 , xn |
дают аналогичное уравнение |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
2hn−−31 (yn−2 − yn−1 )+ hn−−21 (sn−2 + sn−1 )= 2hn−3 (yn−1 − yn )+ hn−2 (sn−1 + sn ). |
]+ [x1 |
, x2 ] |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Можно доказать, что условие |
4 |
|
|
эквивалентно |
|
объединению |
отрезков [x0 , x1 |
|
и |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[xn−2 , xn−1 ]+ [xn−1 , xn ] |
и построению сплайнов по системе n − 2 отрезков внутри |
[a, b]. Этот |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
факт объясняет название «отсутствие узла». |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
5. Если |
|
y = f (x) |
|
- |
|
периодическая функция с периодом |
b − a , то можно воспользо- |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
ваться условием |
s |
0 |
= s |
n |
. |
|
Тогда |
|
|
h |
−1 (s |
n−1 |
+ 2s |
n |
|
) |
+ h−1 |
(2s |
0 |
+ s )= 3[h−2 |
(y |
n |
− y |
n−1 |
)+ h−2 |
(y |
1 |
− y |
0 |
)] |
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
1 |
|
|
n |
|
|
|
|
1 |
|
|
|
|
|||||||||||||||||||||
(выводится аналогично из условия |
P |
/// |
(x |
0 |
)= P |
/// |
(x |
n |
) ). Существуют и другие подходы к зада- |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3,0 |
|
|
|
|
|
|
|
|
3,n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
нию граничных условий. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
Запишем теперь, например, с условием 4 всю систему, симметризировав предвари- |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
тельно первое и последнее уравнение. Получим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
h1−2 s0 + (h1−2 |
− h2−2 )s1 − h2−2 s2 = 2h2−3 (y1 − y2 )− 2h1−3 (y0 − y1 ), i = 0, |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ hi−+11si+1 |
= 3[hi−2 (yi |
− yi−1 )+ hi−+21 (yi+1 |
− yi )], i = 1,2,..., n −1, |
(3.10.4) |
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
hi−1si−1 + 2(hi−1 + hi−+11 )si |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
h−2 |
s |
n−2 |
+ |
(h−2 |
− h |
−2 )s |
n−1 |
− h |
−2 s |
n |
= 2h−3 |
(y |
n−1 |
− y |
n |
) |
− |
2h−3 |
(y |
n−2 |
− y |
n−1 |
), i |
= n. |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
n−1 |
|
|
|
|
n−1 |
|
|
|
|
n |
|
|
|
|
n |
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
n−1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
Эта система, записанная в матричном виде, приводит к трехдиагональной матрице. Действительно,
|
−2 |
−2 |
−2 |
|
−2 |
0 |
|
0 |
|
0 |
|
||
h1 |
h1 |
+ h2 |
−1 ) |
− h2 |
|
|
|
||||||
h−1 |
2(h−1 |
+ h |
h−1 |
0 |
|
0 |
|
0 |
|
||||
|
1 |
1 |
2 |
2(h−1 |
2 |
|
|
|
|
|
|
|
|
|
0 |
h−1 |
|
+ h−1 ) |
h−1 |
|
0 |
|
0 |
|
|||
|
|
|
2 |
|
2 |
3 |
3 |
... |
|
... |
|
||
... |
... |
|
... |
... |
|
|
|||||||
|
0 |
|
0 |
|
|
0 |
−1 |
−1 |
−1 |
|
|
−1 |
|
|
|
|
|
hn−2 |
2(hn−2 |
+ hn−1 ) |
hn−1 |
|
|||||
0 |
|
0 |
|
|
0 |
0 |
h−1 |
2(h−1 |
|
+ h−1 ) |
|||
|
|
|
|
|
|
|
|
|
n−1 |
n−1 |
|
n |
|
0 |
|
0 |
|
|
0 |
0 |
h−2 |
h−2 |
+ h−2 |
||||
|
|
|
|
|
|
|
|
|
n−1 |
n−1 |
|
|
n |
0 |
|
|
|
s0 |
|
|
b0 |
|
||
0 |
|
|
|
s1 |
|
|
b1 |
|
||
|
|
|
|
|
|
|||||
0 |
|
|
|
s2 |
|
|
b2 |
|
||
|
|
|
|
|
|
|||||
... |
|
... |
|
= ... |
, |
|||||
0 |
|
|
|
|
|
|
|
|
|
|
|
|
sn−2 |
|
bn−2 |
|
|||||
h−1 |
|
s |
n−1 |
|
b |
|
||||
n |
|
|
|
|
|
|
n−1 |
|
||
− h |
−2 |
s |
n |
b |
||||||
n |
|
|
|
|
|
|
n |
|
||
где b |
= 2h−3 |
(y |
1 |
− y |
2 |
)− 2h−3 |
(y |
0 |
− y |
1 |
), |
b |
= 3[h−2 |
(y |
1 |
− y |
0 |
)+ h−2 |
(y |
2 |
− y |
1 |
)], ..., |
0 |
2 |
|
|
1 |
|
|
|
1 |
1 |
|
|
2 |
|
|
|
87
