
Спиглазов_Механика материалов для з.о
..pdf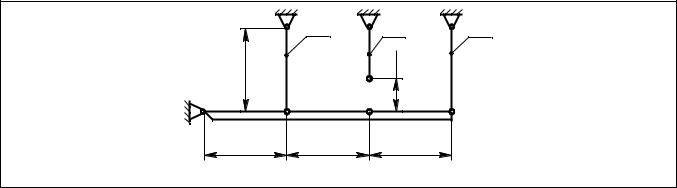
cos(α) |
B '' K |
|
l3 |
|
BB '' |
l3 |
1,16 |
l3 ; |
|
BB '' |
BB '' |
cos(α) |
|||||||
|
|
|
|
|
|
В силу симметричности системы справедливо, что:
l2 l3 ;
Удлинение первого стержня равно смещению точки B ': B ' B'' l1 .
Из анализа геометрических связей между смещениями точек при деформировании системы, получим:
BB' BB'' B' B''; 1,16 l2 l1 – уравнение совместности деформа-
ций.
Используя закон Гука, полум:
|
1,16 |
N2 l2 |
|
|
N1 l1 |
; |
|
2 N |
EA 2,3 N |
; |
|
|
|||
|
|
|
|
|
|
||||||||||
|
|
|
E A |
E A |
|
|
|
1 |
2 |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|||||
N |
1 |
2 103 200 109 |
1 104 2,3 N |
|
|
20 103 1,15 N |
; |
(*) |
|||||||
|
2 |
||||||||||||||
1 |
2 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2. Запишем уравнение равновесия для рассматриваемой системы.
Вравновесии находится сходящаяся система сил (равновесие узла B).
Fx 0; N2 sin(α) N3 sin(α) 0;
N2 N3;
Fy 0; |
N1 N2 cos(α) N3 cos(α) 0; (**) |
Решив совместно уравнения (*) и (**), получим:
N2 N3 6,9 кН;
N1 12,1 кН.
Пример 3:
Абсолютно жесткий брус закреплен шарнирно и удерживается в равновесии тремя стержнями одинаковой площади поперечного сечения. Материал стержней Ст. 3. Второй стержень был изготовлен короче на величину 1 мм .
Дано:
E 200 ГПа ; σ 100 МПа ; A1 A2 A3 2 см2 .
Определить: записать уравнение совместности деформаций.
|
|
1 |
2 |
3 |
1 м |
|
|
|
|
K |
B |
C |
|
D |
1 м |
|
1 м |
1 м |
|
|
исходная система |
|
||

|
|
|
2 |
|
|
|
|
|
|
l |
|
|
|
|
|
|
|
C'' |
|
3 |
|
|
|
|
|
l |
|
|
|
|
|
C' |
|
D' |
|
B' |
|
|
|
|
|
|
|
|
|
|
|
|
K |
B |
1 |
|
C |
δC |
D |
|
|
l |
|
|
|
|
|
деформированная система |
|
||||
Решение:
Из подобия треугольников KBB' KCC ' RDD' получим соотношения для сторон:
|
|
|
BB ' |
|
CC ' |
|
|
DD ' |
; |
|
|
|
|
KB |
KC |
|
KD |
|
|||
|
|
|
|
|
|
|
|
|||
Согласно |
схеме |
деформирования: |
|
BB ' l1 ; |
DD' l3 ; |
|||||
CC ' CC '' C 'C '' l2 . Отсюда получим:
l1 |
|
l2 |
|
l3 |
– уравнение совместности деформаций. |
|
1 |
2 |
3 |
||||
|
|
|
6.5. Учет пластических деформаций при растяжении (сжатии) статически неопределимых стержневых систем.
В ряде случаев для элементов конструкции, выполненных из пластичных материалов или материалов ограниченной пластичности, наблюдается не линейная связь между внутренними усилиями и деформациями. Это характерно при возникновении в материале элемента напряжений превышающих пропорциональности.
Для пластичных материалов при достижении напряжений равных пределу текучести наблюдается рост деформаций при неизменной величине внутреннего усилия. При ограничений этих пластических деформаций другими элементами конструкции в них возникают добавочные усилия равные величине пластической деформации.
Пример: |
|
|
|
|
|
Определить реакцию в опоре при растяжении стержня лощадью |
A 1 см2 |
||||
поставленного с зазором 2 мм . Материал стержня сталь Ст. 3 с пределом те- |
|||||
кучести σт 120 МПа и модулем упругости E 200 ГПа . |
|
|
|||
|
|
|
F/2=10 кН |
|
|
K |
N |
B |
B' B'' |
R |
|
|
|
||||
|
A=1 см2 |
|
|
|
|
|
|
|
F/2=10 кН |
|
|
|
l=2 м |
|
=2 мм |
|
|
Определим усилие в стержне N при котором в материале будут действовать напряжения, соответствующие пределу текучести:
N σт A 120 106 1 10 4 12 103 Н 12 кН ;
Так как величина внешней нагрузки F, вызывающей возникновение продольной силы N, превышает величину соответствующую пределу текучести, то в материале стержня будут возникать как упругие, так и пластические деформации.
Определим величину упругих деформаций с помощью закона Гука:
l |
|
|
N l |
|
|
12 103 2 |
1,2 10 3 м 1,2 мм ; |
|
у |
E A |
200 109 1 10 4 |
||||||
|
|
|
|
|||||
|
|
|
|
|
|
|
||
Определим величину пластической деформации. Полная деформация стержня ограничена опорой в точке B '' и не может превышать зазор . Так как полная деформация состоит из упругой и пластической составляющей, то справедливо выражение:
ly lo BB ' B ' B '' ; Отсюда получим: lo lу 2 1,2 0,8 мм .
Отсеченная часть стержня совместно с опорой в точке B '' под действием внешних сил (F, R)и внутренних усилий (N) находится в равновесии:
Fx 0; N F R 0; R F N 20 12 8 кН.
Ответ: lo 0,8 мм ; R 8 кН .
6.6. Вопросы для самоконтроля.
1.Степень статической неопределимости системы.
1.1.Понятие степени свободы.
1.2.Понятие внутренних связей, определение их количества.
1.3.Понятие внешних связей, определение их количества.
1.4.Понятие степени статической неопределимости системы.
2.Решения статически неопределимых систем на растяжение или сжатие.
2.1.Алгоритм решения.
2.2.Понятие уравнений совместности деформаций, их назначение.
2.3.Деформированная система и правила ее отображения.
2.4.Примеры решения статически неопределимых систем.
2.5.Условная диаграмма деформирования (УДД) при растяжении пластичного материала.
2.6.Характеристики прочности пластичного материала.
2.7.Характеристики деформативности пластичного материала.
2.8.Характеристики пластичности пластичного материала.
2.9.Явление наклепа для пластичного материала.
2.10.Истинная диаграмма деформирования при растяжении пластичного материала.
2.11.Основные физико-механические характеристики (по ИДД).
2.12.Диаграмма сжатия пластичного материала, отличия от диаграммы растяжения.
2.13.Поведение пластичного материала при сжатии.
2.14.Опасные напряжения для пластических материалов.
3.Температурные напряжения.
3.1.Причины возникновения температурных напряжений.
3.2.Температурные деформации.
3.3.Понятие коэффициента линейного температурного расширения.
3.4.Совместное действие температурных и силовых деформаций (от нагрузок).
3.5.Примеры расчета с учетом температурных напряжений.
4.Монтажные напряжения.
4.1.Понятие монтажных напряжений.
4.2.Причины возникновения монтажных напряжений.
4.3.Примеры расчета с учетом монтажных напряжений.
5.Учет пластических деформаций при растяжении (сжатии) статически неопределимых стержневых систем.
К содержанию
7. Теория напряженного и деформированного состояния
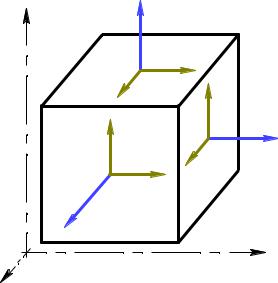
7.1. Напряженное состояние в точке. Главные площадки и главные напряжения.
Через каждую точку нагруженного тела можно провести бесчисленное множество различно ориентированных (плоскостей) площадок. Совокупность напряжений, возникающих на них, характеризует напряженное состояние в данной точке.
y |
|
σy |
|
|
|
τyx |
|
|
τyz |
|
|
τ |
|
τxy |
σx |
zy |
|
||
|
|
|
|
|
|
τxz |
|
σz |
|
τzx |
|
|
|
|
|
|
|
|
x |
z
Напряжение на любой площадке в произвольной точке определяют через проекции напряжений на взаимно перпендикулярные плоскости. Проекции на координатные оси называют компонентами напряжения в точке и обозначают:
σx
σy – нормальные напряжения;
σz
τxy τ yx
τxz τzx – касательные напряжения;
τyz τzy
Первый индекс показывает, какой оси перпендикулярна площадка действия напряжения, второй – какой оси параллельно напряжение.
Нормальное напряжение положительно, если направлено от площадки по нормали, т.е. растягивает. Касательные напряжения отрицательны, если они образуют пару стремящуюся повернуть рассматриваемый элемент вокруг оси по правилу буравчика. Касательные напряжения, действующие на 2-х взаимно перпендикулярных площадках, равны по величине и противоположны по знаку.
Через каждую точку тела можно провести три взаимно перпендикулярные площадки, на которых касательные напряжения равны нулю. Данные площадки называются главными площадками в рассматриваемой точке, а направления нормалей к ним – главными направлениями.
Действующие на главных площадках нормальные напряжения называются главными напряжениями и достигают экстремальных в данной точке значений
(обозначают 1, 2, 3; причем 1 > 2 > 3).
В зависимости от количества главных напряжений в точке различают три вида напряженного состояния:
1.Линейное – когда два главных напряжения равны нулю (растяжение или сжатие в одном направлении);
2.Плоское – когда одно из главных напряжений равно нулю (например растяжение или сжатие в двух направлениях);
3.Объемное – все три главных напряжения не равны нулю.

7.2. Линейное (одноосное) напряженное состояние
ЛНС возникает в теле, когда вектора напряжений ориентированы вдоль одной линии (случай растяжения или сжатия).
σ1 0; σ1 σ1 0.
Определим напряжение, действующее в произвольном сечении растянутого стержня.
В поперечном сечении 1–1:
F |
1 |
N |
F |
N F , |
|
|
|
||||
|
|
|
N . |
||
|
|
|
|
σ |
|
|
1 |
|
|
|
A |
В произвольном сечении 2–2 повернутом на угол относительно поперечного сечения 1–1:
Положительный угол наклона α будем откладывать против часовой стрелки
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
F |
|
|
|
|
|
|
|
|
α |
Nα |
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
2 |
α |
N=F |
σx |
pα |
N |
|
w |
|
pα |
|
|
|
α |
σα |
τα |
α |
||||||||
|
|
|
|
|
|
|
2 |
|
0 |
Aα |
|
|
2 |
|
|
|
|
|
2 |
|
|
9 |
|
|
|
|
1 |
1 |
|
1 |
|
|
|
|
|
|
|
|
1 |
|
A |
Aα |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
n' |
|
A |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
R=F |
|
R=F |
|
|
R=F |
|
|
|
R=F |
|
|
Напряжения в поперечном сечении 1–1:
σ1 1 σx NA FA ;
Площадь наклонного сечения 2–2 под углом α к поперечному:
A2 2 Aα |
A |
; |
|
|
|||
cos(α) |
|||
|
|
На наклонной площадке в направлении нагружения действует напряжение:
p |
N |
|
N cos(α) |
σ |
|
cos(α) ; |
|
|
x |
||||
α |
Aα |
|
A |
|
||
|
|
|
|
|||
Напряжения по нормали к наклонной площадке 2–2 (нормальные напряже-
ния):
σα pα cos(α) σx cos2 (α) ;
Напряжения вдоль наклонной площадки 2–2 (касательные напряжения):
τα pα sin(α) 12 σx sin(2 α) ;

Таким образом компоненты напряжений в любом сечении бруса на произвольной площадке определяются по формулам:
σα σx cos2 (α);
|
|
|
1 |
|
|
(*) |
τ |
|
|
σ |
|
sin(2 α). |
|
α |
|
x |
||||
|
2 |
|
|
|||
|
|
|
|
|
||
Из анализа выражений (*) видно, что при продольном нагружении бруса максимальные нормальные напряжения будут в поперечном сечении бруса, т.е. при угле наклона сечения 2–2 равном нулю ( α 0 ):
σmax σ 0 σx NA ;
При этом касательные напряжения равны нулю.
Максимальные касательные напряжения возникают вдоль площадок (сечение 2–2) под углом α 45 :
τ |
|
τ |
|
|
1 |
σ |
|
|
N |
|
; |
max |
α=45 |
|
x |
2 A |
|||||||
|
|
2 |
|
|
|
||||||
|
|
|
|
|
|
|
|
||||
В продольных сечениях |
(при |
α 90 ) |
|
напряжения отсутствуют, т.е. |
|||||||
σα τα 0.
7.2.1. Закон парности касательных напряжений
Рассмотрим растянутый стержень, выделим две произвольные, взаимно перпендикулярные площадки. Определим нормальные и касательные напряжения на этих площадках.
σα τα
|
|
w |
|
|
0 |
|
|
9 |
|
|
|
+ |
|
|
|
σ |
|
|
|
α |
|
|
τα+90w |
|
|
|
|
τ τ
τ
 τ
τ
|
σ |
|
σ cos2 (α) , τ |
|
|
1 |
σ sin(2α) , |
||
α |
α |
α |
|
||||||
|
|
|
|
2 |
|
||||
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
||
|
σ |
α+90 |
σ cos2 |
α 90 σ sin2 (α) , |
|||||
|
|
|
|
|
|
|
|
||
σα σα+90 σx cos2 (α) σx sin2 (α) σx ;
Сумма нормальных напряжений на двух взаимно 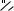
 перпендикулярных площадках равна нормальному напряжению в поперечном сечении.
перпендикулярных площадках равна нормальному напряжению в поперечном сечении.
τα+90 12 σ sin 2 α+90 12 σ sin(2α); ,
τα τα+90 ;
Закон парности касательных напряжений – касательные напряжения на двух взаимно перпендикулярных площадках равны по величине и обратны по знаку.

7.3. Плоское напряженное состояние
Плоское напряженное состояние возникает в том случае, когда вектора всех напряжений лежат в одной плоскости.
σ1 0; σ3 0; σ2 0.
|
σy τ |
τ σ |
|
|
|
σx |
|
x |
α |
|
|
τ |
|
|
σy |
|
|
τ |
Mk |
|
|
|
Mk
Выделим из тела в окрестности произвольной точки бесконечно малую треугольную призму, боковые грани которой перпендикулярны к плоскости чертежа, а высота их равна dz. Приложим к призме те же напряжения, которые действовали на нее до выделения ее из тела.
|
|
|
|
dx |
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
σy |
τyx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
α |
τxy |
|
|
|
τα |
|
O |
σx |
x |
|
α |
|
|
|
|
|
|
|
|
|
|
|
|
|
dy |
|
|
|
|
σ |
|
|
|
|
d |
|
|
α |
|
|
|
|
s |
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Для определения напряжений σα и τα , действующих по наклонной площад-
ке, составим три уравнения равновесия. Вначале составим условие равенства нулю моментов относительно точки О:
τyx dz dx dy2 τ dz dy dx2 0;
Отсюда получаем закон парности касательных напряжений:
τxy τyx ;
Запишем условия равенства нулю суммы проекций сил на направления напряжений σα и τα :

Fσα σα ds dz σ y dz dx sin(α) τ yx dz dx cos(α) ]σx dz dy cos(α) τxy dz dy sin(α) 0;
Fτα τα ds dz σ y dz dx cos(α) τ yx dz dx sin(α)σx dz dy sin(α) τxy dz dy cos(α) 0;
Из схемы очевидно, что: cos(α) |
dy |
, |
sin(α) |
dx |
; |
|
|
|
ds |
ds |
|
|
|
||||
|
|
|
|
|
|
|
||
Подставим значения cos(α) и sin(α) в выражения Fσ |
0; |
и Fτ |
0; а |
|||||
|
|
|
|
|
|
α |
|
α |
затем сократим полученные уравнения на ds dz . В результате получим:
σα σ y sin2 (α) σx cos2 (α) (τ yx τxy ) sin(α) cos(α); τα (σx σ y ) sin(α) cos(α) τ yx sin2 (α) τxy cos2 (α);
С учетом равенства касательных напряжений на перпендикулярных площадках последние две формулы для определения напряжений на наклонных площадках примут вид:
σ |
σ |
|
sin2 (α) σ |
|
cos2 (α) τ |
|
sin(2 α); |
(1) |
|||
α |
|
y |
|
|
|
x |
|
|
xy |
|
|
|
|
|
|
|
|
|
|
||||
|
τ |
|
|
(σx σy ) |
sin(2 α) τ |
|
|
cos(2 α). |
|
||
|
α |
|
xy |
(2) |
|||||||
|
|
|
2 |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|||
Для нормальных напряжение для двух взаимно перпендикулярных площадок под углами α и α 90 справедливо равенство:
σα σα+90o σx σy const ,
т.е. сумма величин нормальных напряжений в двух взаимно перпендикулярных площадках есть величина постоянная.
7.3.1. Главные напряжения и главные площадки
Для определения величин главных напряжений используем формулу расчета нормальных напряжений:
dσα σy 2 sin(α) cos(α) σx 2 cos(α) sin(α) τxy cos(2 α) 2 0; dα
(σy σx ) sin(2 α) 2 τxy cos(2 α) 0 2 τα ,
отсюда находим:
tg(2 α |
|
) |
2 τxy |
, |
(3) |
0 |
|
||||
|
|
σx σ y |
|
||
|
|
|
|
||
или
τ
tg(α0 ) xy
σx σmin
где α0 – углы |
наклона главных площадок к площадке, |
в которой действует |
|||||||||||||||||||||||
напряжение σx . По главным площадкам касательные напряжения равны нулю. |
|||||||||||||||||||||||||
Если угол наклона α0 положителен, |
то его откладывают от направления |
||||||||||||||||||||||||
вектора σx по ходу часовой стрелки, иначе – против часовой стрелки. |
|
||||||||||||||||||||||||
Подставим выражение (3) в формулу (1) найдем |
|
|
|
|
|
|
|||||||||||||||||||
|
σ |
max |
σ |
|
σx |
σ y 1 |
|
|
(σ |
x |
σ |
y |
)2 |
4 τ2 . |
|
(4) |
|||||||||
|
|
|
|
|
1,3 |
|
|
|
2 |
|
2 |
|
|
|
|
|
|
|
|
xy |
|
|
|||
|
|
min |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где σ1,3 – главные напряжения ( σ2 0, так как это плоское напряженное состояние). |
|||||||||||||||||||||||||
Если σx σy , то σmax |
|
откладывается от вектора σx . |
|
|
|
|
|||||||||||||||||||
Площадки, по которым действуют τmax и τmin , называются площадками |
|||||||||||||||||||||||||
сдвига. Их находим, используя формулу (2): |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
dτxy (σ |
x |
σ |
y |
) cos(2 α) 2 τ |
xy |
sin(2 α) 0; |
|
|||||||||||||||||
|
|
dα |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
tg(2 α ) σx σy ; |
|
|
|
|
|
|
(5) |
||||||||||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
2 τxy |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
где α1 – угол наклона площадки сдвига к площадке, по которой действует напря- |
|||||||||||||||||||||||||
жение σx . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Сравним формулы (3) и (5), очевидно, что |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
tg(2 α ) |
|
1 |
|
, |
то есть |
α α |
0 |
45o. |
|
||||||||||||||
|
|
|
|
|
|
1 |
|
tg(2 α0 ) |
|
|
|
|
|
|
|
1 |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Таким образом, площадки сдвига наклонены к главным площадкам под |
|||||||||||||||||||||||||
углами, равными 45о. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Для определения величин τmax и τmin |
|
примем, что в формуле (2) τxy 0 , |
|||||||||||||||||||||||
σx σmax , σy σmin . Кроме того возьмем α 45o. В этом случае: |
|
|
|||||||||||||||||||||||
|
|
|
|
τ |
max |
|
1 (σ |
x |
σ |
y |
)2 |
4 τ2 |
; |
|
|
|
(6) |
||||||||
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
xy |
|
|
|
|
|
|||||
|
|
|
|
|
|
min |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
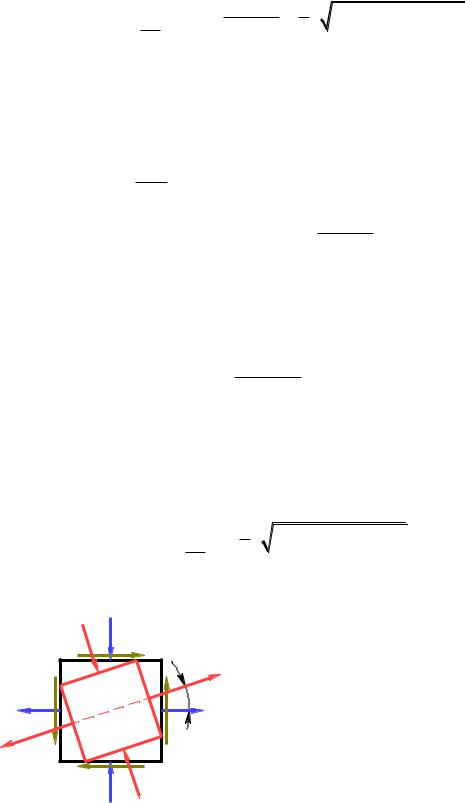
Пример: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
σ3 |
σy |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
τ |
|
α σmax=σ1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
Определить величины главных напряже- |
|||||||||||||||||
τ |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
ний |
|
и |
|
положение |
главной |
площадки: |
||||||||
σx |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
σx |
70 МПа , |
|
|
|
σy |
10 МПа , |
||||||||
|
|
|
|
|
|
σx |
|
|
|
|
|
|
|||||||||||||
|
|
|
τ |
|
|
|
|
τ 30 МПа . |
|
|
|
|
|
|
|||||||||||
σ1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
τ σy |
σmin=σ3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Определяем главное напряжение: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
