
Спиглазов_Механика материалов для з.о
..pdfгде l – расстояние между опорами.
|
|
|
|
|
|
|
E I |
z |
y |
32,1 кН м3 |
; |
|
|
|
|
|
|
|
|
|
max |
|
|
|
|
I |
|
|
|
32,1 103 |
|
|
32,1 103 |
=1240 10 8 м4 1240 cм4 ; |
||||
|
|
|
||||||||||
z |
|
|
|
|
|
|
|
|||||
|
|
|
200 109 10 10 3 |
|||||||||
|
|
|
E y |
|
|
|||||||
|
|
|
|
|
|
|||||||
|
|
|
|
max |
|
|
|
|
|
|
||
Из таблицы сортамента выбираем двутавр с ближайшим большим к рассчитанному значением осевого момента инерции: двутавр № 18.
Из условия прочности для данной балки принят двутавр № 22а, и условия жесткости – № 18. Окончательно принимаем больший двутавр № 22а.
10.5. Вопросы для самоконтроля.
1.Условие жесткости.
1.1.Допускаемый прогиб, определение, диапазон значений.
1.2.Упругая линия балки.
1.3.Угол поворота сечения.
1.4.Прогиб балки, стрела прогиба.
1.5.Правило знаков для угла поворота и прогиба.
1.6.Кривизна упругой линии балки, основные допущения.
1.7.Уравнение углов поворота.
1.8.Уравнение прогибов.
2.Метод начальных параметров при изгибе.
2.1.Уравнение моментов, правила записи.
2.2.Константы интегрирования (начальные параметры) их физический смысл.
2.3.Граничные условия их назначение – определение констант интегрирования.
3.Расчеты на жесткость.
3.1.Условие жесткости.
3.2.Определение максимального прогиба (способы).
3.3.Типы решаемых задач на жесткость.
3.4.Примеры решения задач на жесткость.
К содержанию


11.6. Определение напряжений при кручении стержней круглого поперечного сечения
Воспользуемся законом Гука при кручении (сдвиге):
τ G γ;
Су четом того, что угол сдвига для произвольной точки по радиусу зависит от угла поворота сечений, получим:
τ G ρ |
dφ |
; |
|
dx |
|||
|
(*) |
Рассмотрим равновесие отсеченной части бруса.
|
τ |
|
Mk T – внутренний |
силовой |
|
|
фактор (крутящий момент). |
|
|
|
|
dA |
|
|
|
|
Сила, действующая на площадке |
||
Mk |
|
|
||
|
|
dA от касательных напряжений |
τ опре- |
|
|
|
|
||
|
|
x |
деляется по формуле: |
|
|
|
dF τ dA; |
|
|
|
|
|
|
|
|
|
Момент от силы dF |
относитель- |
Mk |
ρ |
но оси стержня определяется интегра- |
|
|
лом: |
|
|
|
|
|
|
|
dx |
Mk τ ρ dA; |
|
|
|
|
|
|
|
A |
|
С учетом закона Гука при сдвиге получим:
M |
|
|
|
G 2 |
|
d |
dA G |
|
d |
|
|
|
2 dA G |
d |
I |
|
; |
|||||||||||||
k |
|
|
|
|
|
p |
||||||||||||||||||||||||
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
dx |
|
dx |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
A |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
const |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
I p |
|
|
||
|
|
|
|
|
|
|
|
|
|
d |
, |
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|||||||||||||
где – относительный угол закручивания. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
M k |
. |
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
G I p |
|
|
|
|
|
|
||||||||||
Используя уравнение (*), получим: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
τ |
|
G |
d |
, |
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
ρ |
dx |
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
M |
|
|
|
|
τ |
I |
|
|
|
., |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
k |
|
|
|
p |
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ρ |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Отсюда получим: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
τ |
|
M k |
ρ. |
|
|
|
|
|
|
|
|
(**) |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
I p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
где M k – внутренний крутящий момент (берется из эпюр), Ip – полярный момент
инерции.
Формула (**) позволяет рассчитать значение напряжений в любой точке при кручении круглого вала.
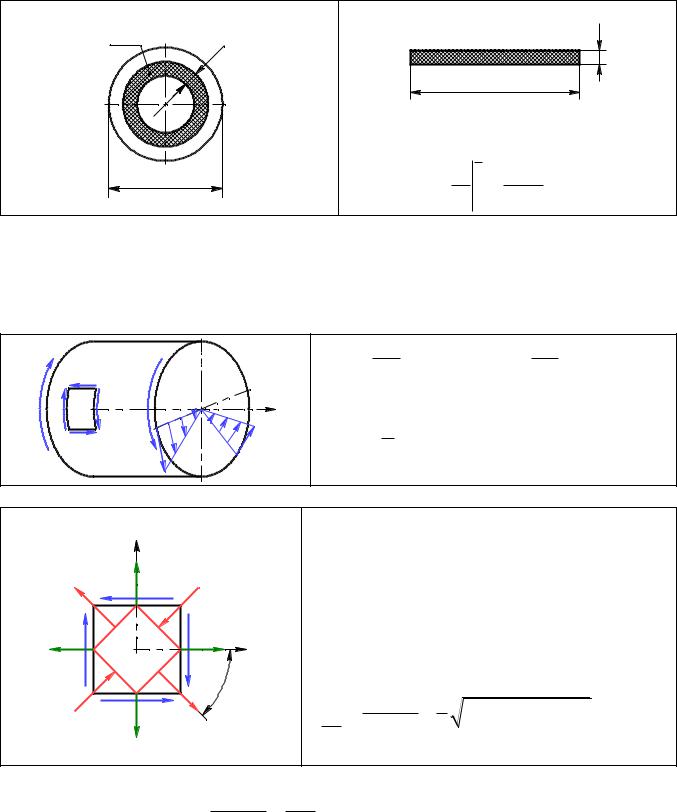
Рассчитаем полярный момент для круглого сечения.
|
|
A |
|
dρ |
|
|
|
|
|
|
|
|
|
|
dρ |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
ρ |
|
|
|
|
|
|
|
|
|
2πρ |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
I p ρ2dA 2 π ρ ρ2dρ |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
A |
|
|
A |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d |
|
|
|
|
|
|
|
|
|
d |
|
|
|
|
|
|
|
|
ρ4 2 |
|
π d 4 |
4 |
||
|
|
|
|
|
|
|
|
|
|
2 π 4 0 |
|
|
|
0,1 d ; |
||||
|
|
|
|
|
|
|
|
|
|
|
32 |
|||||||
11.6.1. Распределение касательных напряжений при кручении |
|
|||||||||||||||||
Из формулы (*) следует, что касательные напряжения изменяются по высо- |
||||||||||||||||||
те сечения линейно, равны нулю на оси вращения и максимальны на поверхности |
||||||||||||||||||
вала. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
τ |
|
Mk |
|
|
|
|
|
|
M k |
const C; |
τ M k C ρ; |
|||||||
|
|
|
|
|
|
|
|
|
I p |
|
|
|
|
|
|
I p |
|
|
|
|
|
|
|
|
|
|
x |
при ρ 0: |
τ 0; |
|
|
|
|
|
|||
|
τ |
τmax |
|
|
|
|
τ |
при ρ d : |
τ τmax ; |
|
|
|
|
|
||||
Mk |
|
|
|
|
|
max |
|
2 |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рассмотрим напряженное состояние в точке на поверхности стержня. |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
В виду отсутствия поперечных и про- |
||||||||
|
|
y |
|
|
|
|
|
|
дольных сил: |
|
|
|
|
|
|
|
||
|
|
σy |
|
|
|
|
|
|
|
|
σx |
σy |
σz |
0; |
|
|||
|
σ1 τ |
|
σ3 |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
При кручении на главных площадках |
|||||||||||
σ |
τ |
|
|
|
σ |
|
|
|
действуют два главных напряжения, таким |
|||||||||
|
|
|
x |
|
|
образом, |
материал |
испытывает |
плоское |
|||||||||
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
τ |
w |
x |
|
напряженное состояние. |
Главные напряже- |
|||||||||
|
|
|
|
|
|
ния определим из выражения: |
|
|||||||||||
σ3 |
|
|
5 |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
4 |
|
|
|
|
σx σ y |
1 |
|
|
|
|
|
|
|||
|
|
σ |
τ |
σ1 |
|
|
|
|
σmax |
(σx |
σ y )2 |
4 τ2 |
τ; |
|||||
|
|
y |
|
|
|
|
|
|
min |
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
σmax =σ1 τ; σ2 0; |
σmin =σ3 τ; |
|||||||
Угол наклона главных площадок: |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
tg(2 α) |
|
2 τ |
|
2 τ ; |
|
2 α 90 |
|
α 45 ; |
|
||||||
|
|
|
|
|
σy σx |
0 |
|
|
|
|
|
|
|
|
|
|||
При кручении главные площадки будут повернуты к оси x стержня под уг- |
||||||||||||||||||
лом 45 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
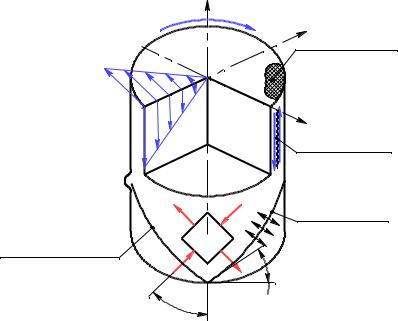
11.6.2. Поведение различных материалов при кручении.
|
|
|
x |
|
Mk |
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
плоскость среза |
|
|
|
|
|
|
пласт. мат. |
τ |
|
|
|
|
|
|
|
|
|
|
|
|
τ z |
|
τ |
|
|
|
|
прод. трещина |
|
|
|
|
|
τ |
древесина |
|
|
|
|
|
|
|
|
σ1 |
σ |
3 |
σ1 |
линия разрыва |
|
|
|
|
||||
|
|
|
|
|||
|
|
|
|
|
|
хрупкий мат. |
складка |
σ3 |
|
|
|
|
|
тонкост. оболочка |
|
|
|
|
|
|
(труба) |
|
|
|
|
σ1 |
|
|
4 |
5 |
w |
|
|
|
|
|
|
45w |
|
||
|
|
|
|
|
||
|
|
|
|
|
|
|
Пластичный материал гораздо хуже сопротивляется деформации сдвига, чем деформации растяжения-сжатия. Следовательно, разрушение волокон из пластичного материала происходит в плоскости поперечного сечения от действия касательных напряжений τ yz .
Хрупкие материалы плохо работают на растяжение, следовательно, разрушение волокон из хрупких материалов будет происходить от действия главного растягивающего напряжения 1 по винтовой линии, наклоненной к продольной оси под углом примерно 45 .
Волокнистые материалы (дерево). Так как эти материалы плохо сопротивляются сдвигу вдоль волокон, то их разрушение при кручении происходит от действия касательных напряжений вдоль волокон τxz , τxy .
Цилиндрические пустотелые оболочки при кручении теряют свою перво-
начальную форму с образованием складок, наклоненных под углом примерно 45 (называется – местные потери устойчивости формы).
11.7.Расчет на прочность при кручении
Вобщем случае условие прочности по касательным напряжениям имеет
вид:
τmax τ ,
Трансформирую формулу (**), получим условие прочности при кручении стержня круглого сечения:
|
τmax |
M max |
r [τ], |
|
k |
||
|
I p |
||
|
|
|
|
где r |
– наружный радиус стержня; M max |
– максимальный крутящий момент, при- |
|
|
k |
|
|
нимают из эпюры моментов.

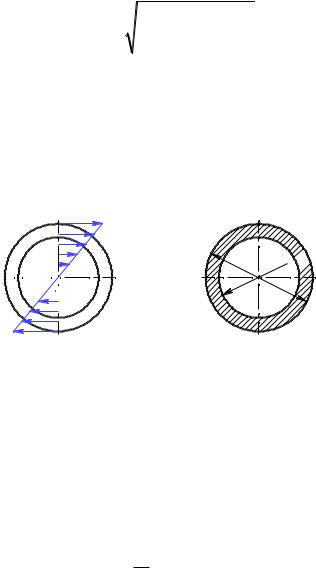

 τ
τ τ
τ

 C'
C' 





 0
0
