Спиглазов_Механика материалов для з.о

Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Белорусский государственный технологический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

sin(2 37,1) 907,5 см4 ;

..pdf

Скачиваний:

Добавлен:

26.03.2015

Размер:

3.48 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 1112 / 1812 13 14 15 16 17 18 > Следующая >>>

dIu Iz 2 cos(α) ( sin(α)) Izy 2 cos(2 α) I y 2 sin(α) dα

	(I y Iz ) sin(2 α) 2 Izy cos(2 α)
	Iz	I y	1
2				sin(2 α) Izy	cos(2 α)	2	Iuv	0;
2			2	sin(2 α) Izy	cos(2 α)	2	Iuv	0;
			2

Таким образом, производная от осевого момента равна центробежному моменту. Следовательно, если осевой момент экстремальный, то центробежный относительно той же оси равен нулю.

Центробежный момент относительно главных осей равен нулю.

Главные оси всегда одни.

Главные оси всегда проходят через центр тяжести сечения.

Если сечение имеет ось симметрии, то эта ось является главной. Вторая главная ось будет проходить через центр тяжести перпендикулярно первой оси.

Если сечение не имеет ни одной оси симметрии, то определить положение главных центральных осей можно исходя из того, что центробежный момент относительно них равен нулю.

Iz I y

sin(2 α) I

cos(2 α) 0;

I y

tg(2 ) I

;

tg(2 α)

2 Izy

(4)

Iz I y

Для определения угла поворота главных осей относительно произвольных

центральных предлагается формула:

tg(α)

Izy

(5)

Imin

Угол α откладывается от оси z. Положительное значение – против часовой

стрелки, отрицательное – по часовой.

Для уравнения (4) если Iz

I y , то угол дает положение оси с максималь-

ным моментом инерции (u), и наоборот, при Iz

I y

– положение оси с минималь-

ным моментом инерции (v).

Выражение (5) всегда определяет положение оси с максимальным моментом инерции.

Если известны моменты инерции относительно случайных центральных осей сечения Iz , I y и известен центробежный момент Izy , то экстремальные мо-

менты инерции для главных осей будут определяться формулами:

		Iz I y	1
I max				Iz I y 2 4 Izy2 .
		2	2
	min

Иногда в подобных расчетах пользуются понятием радиуса инерции iz, м.

iz 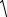IAz ; iy IAy .

8.8. Примеры решения задач на определение геометрических характеристик

Пример 1:

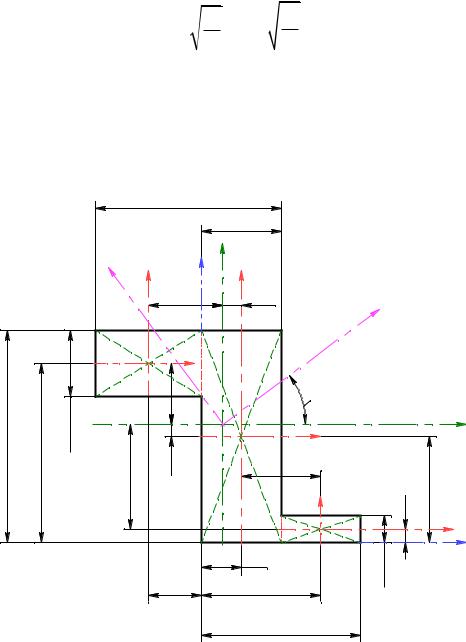
Для заданного сечения определить положение главных центральных осей и величины главных моментов инерции.

		7 см
				3 см
	y	y0		yс y
	1			2
	v	b1		b2		u
						u
	c1	z1
		z1
	м	1			α = 36,2w
		1					zс
		а	c				zс
8см y	2,5 c		c
8см y	2,5 c	2		c2	z2
1				c2	z2
	3	а			b3	2
	а				y3	y
					y3	y
						3
							z3
		0		z2	c3	1 см	z0
		z1		z3		1 см
		z1		z3
				6 см
1. Разобьем сложное сечение на ряд простейших фигур.
а) определим границы фигур;
б) определим положения центров тяжести фигур;
в) проведем центральные оси для каждой из фигур ( zi , yi );
г) определим геометрические характеристики каждой из фигур:
– первая фигура (прямоугольник):

				A b h 4 2,5 10 см2				;
				1
Iz		b h3	4 2,53	5, 21 см4 ;	I y		h b3		2,5 43	13,33 см4 ;
Iz			12	5, 21 см4 ;	I y			12		13,33 см4 ;
1	12		12		1	12		12
1					1

– вторая фигура (прямоугольник):

				A b h 3 8 24 см2					;
					2
Iz			b h3	3 83	128 см4 ; I y			h b3		8 33	18 см4 ;
Iz				12	128 см4 ; I y					12	18 см4 ;
	2	12		12		2	12			12
	2					2

– третья фигура (прямоугольник):

					A b h 3 1 3 см2				;
					3
Iz			b h3	3 13	0, 25 см4 ; I y			h b3		1 33	2, 25 см4 ;
Iz				12	0, 25 см4 ; I y					12	2, 25 см4 ;
	2	12		12		2	12			12
	2					2

2.Зададим положение начальной системы координат (нулевых осей).

3.Определим положения центров тяжести простых фигур относительно нулевых осей

( zi , yi ).

– первая фигура (прямоугольник):

c1 2;6,75

– вторая фигура (прямоугольник):

c2 1,5;4

– третья фигура (прямоугольник):

c3 4,5;0,5

z1 2 см; y1 6,75 см;

z2 1,5 см; y2 4 см;

z3 4,5 см; y3 0,5 см;

4. Определяем положение центра тяжести всего сечения. а) координаты центра тяжести относительно нулевых осей:

yi Ai

y1 A1 y2 A2 y3 A3

6,75 10 4 24 0,5 3

i 1

4, 46 см;

A1 A2 A3

10 24 3

z1 A1 z2 A2 z3 A3

2 10 1,5 24 4 3

i 1

0,76 см;

A1 A2 A3

10 24 3

б) указываем положение центра тяжести всего сечения и проводим центральные оси

( zc , yc ).

5. Определяем осевые моменты инерции всего сечения относительно осей zc и yc (теорема о параллельном переносе осей).

а) определяем смещения центров тяжести простых фигур относительно центра тяжести всего сечения

– вдоль оси yc :

a1 y1 yc 6,75 4, 46 2, 29 см; a2 y2 yc 4 4, 46 0, 46 см; a3 y3 yc 0,5 4, 46 3,96 см;

– вдоль оси zc :

b1 z1 zc 2 0,76 2,76 см; b2 z2 zc 1,5 0,76 0,74 см;

b3 z3 zc 4,5 0,76 3,74 см;

б) рассчитаем осевые моменты инерции:

cIzi ai 2 Ai Iz1 a12 A1 Iz2 2 A2 Iz3 a32 A3

5, 21 (2, 29)2 10 128 ( 0, 46)2 24 0, 25 ( 3,96)2 3 238 см4 ;Iz a2n

cI yi bi 2 Ai I y1 b12 A1 I y2 2 A2 I y3 b32 A3

i 1

13,33 ( 2,76)2 10 18 (0,74)2 24 2, 25 (3,74)2 3 164,9 см4 ;

6.Определим центробежный момент инерции сеченияI y b2n

Ai Iz y

Iz y

a1 b1 A1

a2 b2 A2

Iz y

a3 b3 A3;

c c

i 1

i i

1 1

3 3

Iz y 0;

Iz y 0 – так как простые фигуры симметричны.

Отсюда:

Izc yc 0 2,29 ( 2,76) 10 0 0,46 0,74 24 0 3,96 3,74 3 115,8 см4 ;

7. Определяем величины главных моментов инерции

Izc

I yc

I max

I y

4 Iz2 y ,

c c

min

238 164,9

max

238 164,9 2

4 115,8 2 201, 45 121, 43 см4 ;

min

max

322,88 см4 ;

min

80,02 см4

;

Моменты инерции всегда имеют положительное значение. Проверка: Iu Iv Izc I yc const;

322,88 80,02 238 164,9; 402,9=402,9.

5. Определим положение главных осей (u, v)относительно центральных осей zcyc,:

tg(2 α)	2 Izy				2 ( 115,8)	3,17;	α 36, 2 ;
	I	z	I	y	238 164,9

tg(α)			Izy		115,8	0,73;	α 36, 2 ;
	I	z	I		238 80,02
				min

Угол положителен, поэтому откладываем его относительно оси zc против часовой

стрелки. Полученное направление и даст положение оси с максимальным значением момента инерции (ось u).

Пример 2:

Для заданного сечения, состоящего из равнополочного уголка 75 7 мм, полосы 1,2 20 см и двутавра №16 найти положение главных осей и значения главных моментов инерции.

1. Выписываем и рассчитываем геометрические характеристики составляющих фигур:

1) равнополочный уголок 75 75 7 :

A 10,1 cм2

;

53,3 см4 ; I

max

84,6 см4

; I

min

22,1 см4

;

z0 2,1 см;

B1 7,5 см.

2) пластина (1,2 20 см):

		A b h 1,2 20 24 cм2 ; I														b h3			1, 2 203	800 см4 ;
		A b h 1,2 20 24 cм2 ; I										z2								800 см4 ;
	2											z2			12		12
															12		12
		I				h b3	20 1, 23				2,88 см4 ; B 1,2 см; H										20 см.
		I	y								2,88 см4 ; B 1,2 см; H									2	20 см.
			y	2	12				12						2					2
				2	12				12
	3) двутавр №16 (необходимо учитывать поворот фигуры на 90 ):
		A 21,5 cм2 ;					I	z		77,6 см4 ;			I	y	945 см4 ; B 9 см; H							3	16 см.
	2							z						y			3					3
								3						3
	Полученные геометрические характеристики занесем в таблицу:
№		Фигура			A			z	i		y					a			b		I z		I y	Iz y
						i			i		i					i			i		i		i	i i
1		уголок			10,1		11,3				10,1				5,89			5,54			53,3		53,3	-31,2
2		пласт.			24		8,6				5,5				1,29			2,84			800		2,88	0
3		двут.			21,5			0			0			–4,21				–5,76			77,6		945	0

		y0	yc
	u	y			y2	y1
	u	3
		3
			z2	b1					v		м
			z2								м
			z1								c
			z1						0		7,5
			zc			c1			z	z1	7,5
			zc
			b3	b2		1		1	2	z2
см						a		y a		z2
см						a		y a
20					c2						zc
20			с
			с			3	2		c
						3	2		c
см		c3				a y			y	z3	z0
8,1		0
		16 см			1,2 см
2. Зададим положение начальной системы координат (нулевых осей).
За начало отсчета выберем точку с3 – центр тяжести третьей фигуры.
3. Определим положения центров тяжести простых фигур относительно нулевых осей
( zi , yi ).
– первая фигура (прямоугольник):

z1 H23 B2 z0 162 1, 2 2,1 11,3 см;

y1 H2 B23 B1 z0 20 92 7,5 2,1 10,1 см; c2 11,3;10,1 ;

– вторая фигура (прямоугольник):

1, 2

8,6 см; y

5,5 см;

c2 8,6;5,5 ;

– третья фигура (прямоугольник):

c3 0;0

0 см; y3

0 см;

4. Определяем положение центра тяжести всего сечения.

а) координаты центра тяжести относительно нулевых осей:

yi Ai

y1 A1

10,1 10,1 5,5 24 0 21,5

i 1

4, 21 см;

A1 A2 A3

10,1 24 21,5

zi Ai

z1 A1

z2 A2

z3 A3

11,3 10,1 8,6 24 0 21,5

i 1

5,76 см;

A1 A2 A3

10,1 24 21,5

б) указываем положение центра тяжести всего сечения и проводим центральные оси

( zc , yc ).

а) определяем смещения центров тяжести простых фигур относительно центра тяжести всего сечения

– вдоль оси yc :

a1 y1 yc 10,1 4, 21 5,89 см; a2 y2 yc 5,5 4, 21 1, 29 см; a3 y3 yc 0 4, 21 4, 21 см;

– вдоль оси zc :

b1 z1 zc 11,3 5,76 5,54 см; b2 z2 zc 8,6 5,76 2,84 см; b3 z3 zc 0 5,76 5,76 см;

б) рассчитаем осевые моменты инерции:

cIzi ai 2 Ai Iz1 a12 A1 Iz2 2 A2 I z3 a32 A3

53,3 (5,89)2 10,1 800 (1, 29)2 24 77,6 ( 4, 21)2 21,5 1702,3 см4 ;Iz a2n

cI yi bi 2 Ai I y1 b12 A1 I y2 2 A2 I y3 b32 A3

53,3 (5,54)2 10,1 2,88 (2,84)2 24 945 ( 5,76)2 21,5 2218,1 см4 ;I y b2n

6. Определим центробежный момент инерции сечения

Ai Iz y

Iz y

a1 b1 A1

a2 b2 A2

Iz y

a3 b3 A3;

c c

i 1

i i

1 1

3 3

Iz y

0 – так как фигуры симметричны.

Равнополочный уголок не симметричен относительно центральных осей. Расчет центробежного момента инерции для уголков (равнополочных и неравнополочных) осуществляют по формуле:

Izy Iz Imin I y Imin ;

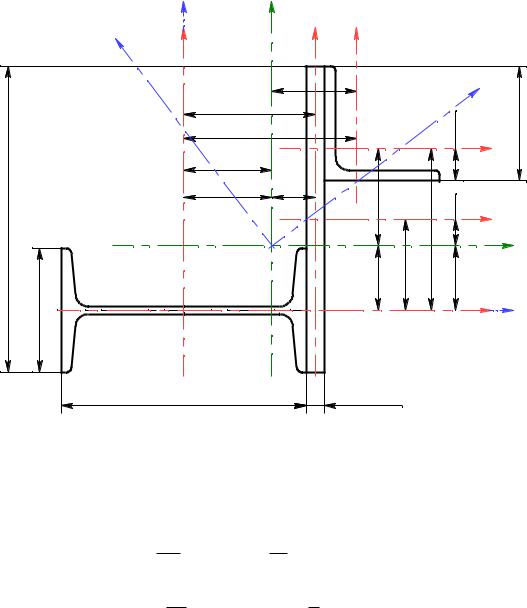
Выбор знака «+» или «–» зависит от ориентации уголка в плоскости. Правило знаков для уголков:

Таким образом:

Iz1y1 Iz1 Imin I y1 Imin 53,3 22,1 53,3 22,1 31,2 см4 ;

Отсюда центробежный момент инерции всего сечения:

Izc yc 31,2 5,89 5,54 10,1 0 1,29 2,84 24 0 4,21 ( 5,76) 21,5 907,7 см4 ;

7. Определяем величины главных моментов инерции.

Izc I yc

I max

I y

2 4 Iz2 y

c c

min

1702,3 2218,1

max

1702,3 2218,1 2

4 907,1 2 1960, 2 943,1 см4 ;

min

max

2903,3 см4 ;

min

1017,1см4 ;

Моменты инерции всегда имеют положительное значение.

Проверка: Iu Iv Iz

I y

const;

2903,3 1017,1 1702,3 2218,1; 3920,4=3920,4.

5. Определим положение главных осей (u, v)относительно центральных осей zcyc,:

tg(2 α)	2 Izy				2 907,7	3,51;	α 37,1 ;

	I	z	I	y	1702,3 2218,1

Угол положителен, поэтому откладываем его относительно оси zc против часовой стрелки. Полученное направление и даст положение оси с минимальным значением момента инерции (ось v), так как Iz I y .

Проверка:

Рассчитаем центробежный момент инерции при повороте главных осей к центральным (на угол ):

Погрешность:

%П	907,5	907,7	100% 0,022% 3%.

	907,5	907,7

		2

8.8. Вопросы для самоконтроля.

1.Основные геометрические характеристики плоских сечений и их назначение в механике материалов и конструкций.

2.Статический момент сечений.

2.1.Физический смысл статического момента инерции.

2.2.Способ расчета для сечений произвольной формы.

2.3.Единицы измерения.

3.Центр тяжести поперечного плоского сечения.

3.1.Использование статического момента при расчете положения центра тяжести сечения.

3.2.Понятие и назначение начальных осей.

3.3.Понятие центральных осей.

3.4.Основные выводы.

3.5.Центры тяжести сечений простых геометрических фигур.

3.6.Порядок определения центра тяжести сложных сечений, приме-

ры.

4.Моменты инерции и сопротивления.

4.1.Физический смысл моментов инерции, их назначение.

4.2.Осевые моменты инерции.

4.3.Полярный момент инерции.

4.4.Центробежный момент инерции.

4.5.Способ расчета для сечений произвольной формы.

4.6.Единицы измерения.

4.7.Физический смысл моментов сопротивления, их назначение.

4.8.Правила расчета моментов сопротивления.

4.9.Моменты инерции и моменты сопротивления простых фигур.

4.10.Моменты инерции и моменты сопротивления профильных сече-

ний.

5.Центробежный момент инерции.

5.1.Понятие центробежного момента инерции, его назначение.

5.2.Понятие главных центральных осей, их назначение.

6.Зависимости между моментами инерции при параллельном переносе осей.

6.1.Основные принципы изменения величины моментов инерции при параллельном переносе осей.

6.2.Основные расчетные формулы.

7.Зависимость между моментами инерции при повороте осей.

7.1.Основные принципы изменения величины моментов инерции при повороте осей.

7.2.Основные расчетные формулы.

8.Главные оси сечения.

8.1.Главные центральные оси сечения и их назначение.

8.2.Основные правила расположения главных осей сечения.

8.3.Центробежный момент инерции относительно главных осей.

8.4.Главные моменты инерции сечения и их назначение.

8.5.Определение положения главных осей сечения, основные пра-

вила.

8.6.Радиус инерции сечений.

8.7.Основные расчетные формулы.

9.Примеры задач на определение геометрических характеристик.

К содержанию

9. Изгиб

9.1. Общие положения

Изгиб – это такой вид нагружения, при котором в поперечных сечениях балки возникает внутренний поперечный силовой фактор и изгибающий момент.

Виды изгиба:

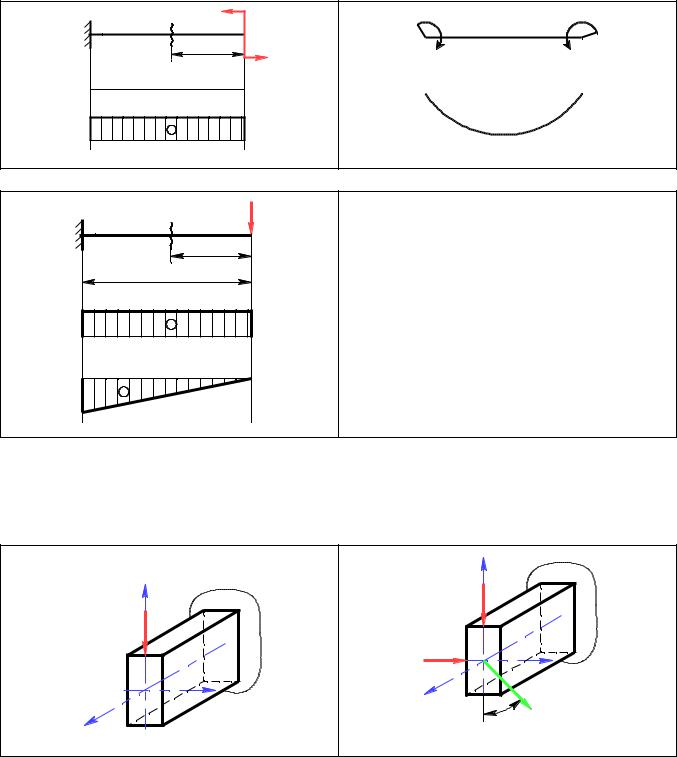
1. Чистый изгиб – в поперечных сечениях действует только изгибающий момент.

M M

			M
	x
	эп. Q (Н)		"+"
			"+"
			0	сжатые волокна
М	эп. М (Н*м)	М	"-"	сжатые волокна
М	эп. М (Н*м)	М
	+		"+"
			0	растянутые волокна
			"-"	растянутые волокна
2. Поперечный изгиб.
			F
	x
	l
F	эп. Q (Н)		F	– в поперечных сечениях действуют изгибаю-
				– в поперечных сечениях действуют изгибаю-
	+		"+"	щий момент и поперечная сила
			0
			"-"
	эп. М (Н*м)		"+"
	-		0
	-		"-"
	Fl

Изгиб бывает плоским (или прямым) и неплоским (или косым).

Прямой изгиб наблюдается в том случае, если плоскость действия пары сил (т.е. изгибающего момента) совпадают с одной из главных осей сечения.

3. Косой изгиб наблюдается тогда, когда плоскость действия изгибающего момента не совпадает с главной осью.

	v
		F
	c	u
x		u
x
	плоский изгиб

	v
		F1
F2	c	u
x		u
x
		R
		α
	косой изгиб

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 1112 / 1812 13 14 15 16 17 18 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
21.08.2019388.41 Кб3Социализация.rtf
#
27.11.201942.87 Кб8Социология. Культ личности.docx
#
24.04.2019165.89 Кб2Социология_материалы_ТДС.doc
#
26.03.201534.83 Кб21Специфика проектирования....docx
#
26.03.2015185.86 Кб27Спецификация(ТОЛЬКО 2 ЛИСТА).doc
#
26.03.20153.48 Mб25Спиглазов_Механика материалов для з.о..pdf
#
26.03.201530.33 Кб51Список частотных отрезков.docx
#
26.03.201546.59 Кб73справка о доходах.doc
#
27.11.201969.04 Кб18Сравнительный анализ стратегии урегулирования с...docx
#
26.03.2015384.51 Кб17СТАНДАРТ БГТУ 12.05.2007-только прилож.doc
#
26.03.2015573.44 Кб44СТАНДАРТ БГТУ 12.05.2007.doc