Файловый архив студентов. Файловый архив студентов.
1262 вуза, 4625 предмета.
/ Регистрация
FAQ Обратная связь Вопросы и предложения
Добавил:
Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.
Вуз:
Белорусский государственный технологический университет
Предмет:
[НЕСОРТИРОВАННОЕ]
Файл:

Спиглазов_Механика материалов для з.о

..pdf
Скачиваний:
25
Добавлен:
26.03.2015
Размер:
3.48 Mб
Скачать
☆

 

Sz

y A

y

2

A ... y

n

A

y

i

1 1

 

2

n

;

 

 

 

 

 

 

c

Ai

 

A1 A2 ... An

 

 

 

 

 

 

 

 

где zi , yi – координаты центров тяжести каждой из простейших фигур относи-

тельно осей некоторой начальной системы координат.

Если фигура имеет ось симметрии, то статический момент относительно нее равен нулю.

Основные вывод:

1. центр тяжести всегда лежит на оси симметрии;

2. при наличии двух и более осей симметрии, центр тяжести фигуры лежит в точке пересечения этих осей.

8.2.1. Центры тяжести сечений простых геометрических фигур.

 

 

 

yc

 

 

 

 

 

 

yc

 

 

 

 

 

 

 

yc

 

 

 

 

 

 

 

h

h/2

с

zc

 

d

zc

 

h h/3

c

zc

 

 

 

c

 

 

 

 

 

 

 

 

 

 

b/2

 

 

 

 

 

 

 

 

b/3

 

 

 

 

b

 

 

 

 

 

 

 

b

 

 

 

 

yc

 

yc

 

 

 

 

yc

 

 

 

 

 

 

 

 

 

π )

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

h

h/3

 

c

zc

c

 

zc

4R/(3

R

c

 

zc

 

 

 

 

 

 

 

 

 

 

 

 

 

 

b/2

 

 

 

 

 

 

 

 

 

 

 

 

b

 

 

 

 

 

 

 

 

 

 

 

8.2.2. Порядок определения центра тяжести сложных сечений.

 

1.Разбиваем сложное сечение на ряд простых фигур (чем проще фигура, тем лучше);

2.Определяем геометрические характеристики простых фигур (положение центров тяжести и площади поперечных сечений), указываем центральные оси для каждой из фигур;

3.Обозначаем (или выбираем из ранее обозначенных) начальную координатную систему;

4.Определяем положение центров тяжести каждой из простейших фигур от-

носительно начальных осей: ci (zi , yi ) ;

 

5. Рассчитываем координаты центра тяжести относительно начальных осей.

 

Пример 1:

 

 

 

 

 

 

 

 

 

Определить положение центра тяжести сечения.

 

 

 

 

 

 

 

 

 

 

 

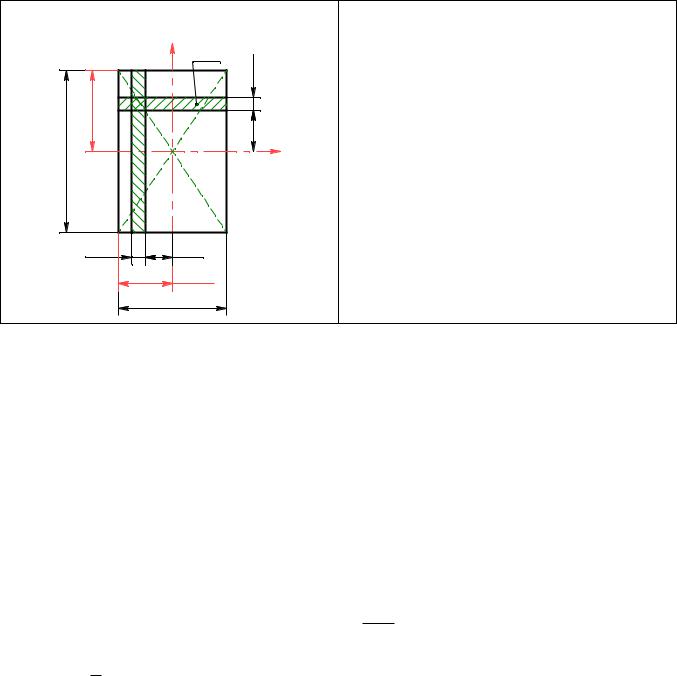
1. разбиваем сложное сечение на

 

 

yс

 

 

 

 

 

простейшие фигуры и определяем

 

 

 

 

 

 

 

их геометрические характеристики.

 

y0

y2

y1

 

cм

 

 

 

1

 

 

 

A1 8 3 24 см2 ;

 

 

 

 

 

 

 

 

 

 

 

 

3

 

 

 

 

 

 

 

 

с1

 

z1

 

 

 

2

;

 

 

 

 

 

 

 

 

 

A2 9 3 27 см

 

2

 

z1

 

 

 

 

A3 8 3 24 см2 ;

см

 

 

 

 

 

 

1

2.

выбираем начальную

систему

 

 

с

 

zс

 

y

с2

 

 

 

координат z0 y0 .

 

15

 

 

z2

z3

 

 

 

 

 

 

 

2

 

3.

определяем положение центров

 

z2

 

y3

 

 

=y

 

тяжести каждой из простейших фи-

 

 

 

 

 

3

с

 

гур относительно начальных осей.

 

 

 

 

 

y y

 

 

 

 

 

 

 

 

 

 

 

3

 

с3

 

z3

 

 

 

c (4;13,5);

 

 

 

 

 

 

 

z0

 

1

 

 

 

 

 

 

 

 

 

z1 4 см; y1 13,5 см.

 

zс

 

 

 

 

 

 

 

 

 

 

 

см

 

 

 

c2 (1,5;7,5);

 

 

 

 

 

 

 

 

 

 

 

 

3 см

 

 

 

z2 1,5 см; y2 7,5 см.

 

 

 

 

 

3

 

 

 

 

 

 

8 см

 

 

 

c3 (4;1,5);

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

z3 4 см; y3 1,5 см.

 

4. рассчитываем положение центра тяжести.

 

 

 

 

z Syi

z1 A1 z2 A2 z3 A3

 

 

4 24 1,5 27 4 24

3,1 см;

 

 

 

 

c

Ai

A1 A2 A3

 

 

 

24 27 24

 

 

 

 

 

y Szi

y1 A1

y2 A2 y3 A3

 

13,5 24 7,5 27 1,5 24

7,5 см;

 

 

 

c

 

Ai

A1 A2 A3

 

 

 

24 27 24

 

 

 

 

 

Так как сечение имеет горизонтальную ось симметрии, то вертикальное смещение центра тяжести относительно начальной оси z0 можно было не рассчитывать.

Пример 2:

Определить положение центра тяжести сечения.

 

 

y0

yс

 

 

 

 

 

y , y , y

 

 

 

 

 

с

 

 

 

 

1

2

 

 

=1,3 см

 

с

 

 

zс

 

y

 

 

 

 

с

 

 

 

 

 

см

см

 

с1

 

z1

z0

15

 

 

 

z2

 

 

6

 

с2

 

 

см

 

 

 

 

 

 

=-3

 

 

 

 

 

 

2

 

 

 

 

 

 

y

 

 

6 см

 

 

 

 

 

8 см

 

 

 

1. разбиваем сложное сечение на простейшие фигуры и определяем их геометрические характеристики.

A1 15 8 120 см2 ;

A2 6 6 36 см2 ;

2.выбираем начальную систему координат z0 y0 .

3.определяем положение центров тяжести

каждой из простейших фигур относительно начальных осей.

c1(0;0);

z1 0 см; y1 0 см.

c2 (0; 3);

z2 0 см; y2 3 см.

4. рассчитываем положение центра тяжести.

z

 

Syi

 

z1 A1 z2

A2

 

0 120

0 36

0 см; – фигура симметрична относи-

c

 

 

 

 

 

 

 

Ai

 

A1 A2

 

 

120

36

 

 

 

 

 

 

 

 

 

 

тельно вертикальной оси;

 

 

 

y Szi

y1 A1

y2 A2

 

0 120 ( 3) ( 36)

1,3 см;

 

 

 

 

 

 

 

 

 

c

Ai

 

A1

A2

 

 

 

120 ( 36)

 

 

 

 

 

 

 

 

Если простейшая фигура не содержит материала (является пустотой) то в формулах значение площади этой фигуры подставляют со знаком «–».

8.3. Моменты инерции и сопротивления.

y

 

z

dA

 

ρ

y

0

 

z

Центробежный момент инерции:

Моменты инерции:

– осевые:

 

 

Iz

y2dA;

 

 

 

A

 

 

I y

z2dA;

 

 

 

A

 

 

– полярный:

 

Iρ ρ2dA y2dA z2dA; – так как:

 

A

A

A

ρ2 z2 y2 .

 

 

Отсюда: I

Iz

I y .

Izy ( y z)dA.

A

Единицы измерения моментов инерции – м4.

Осевые и полярный момент инерции всегда положительны, центробежный момент может быть как положительным, так и отрицательным.

Для упрощения некоторых видов расчетов для симметричных фигур вводят понятие осевых и полярных моментов сопротивления:

W

I

z

, W

 

I y

, W

 

 

I p

.

 

 

 

p

 

z

 

 

y

 

ymax

 

 

max

 

 

ymax

 

 

 

 

 

Примечание: Моменты инерции для сложных фигур определяют как сумму моментов инерции более простых составляющих элементов с учетом смещений их центров тяжести.

Моменты сопротивления для сложных сечений нельзя определять как сумму моментов сопротивления простых фигур – их рассчитывают через моменты инерции!!!

8.3.1Моменты инерции и моменты сопротивления простых фигур.

1.Прямоугольник:

 

yc

dA

 

 

 

 

 

 

dy

 

Iz

2

 

 

h/2

 

 

y

dA;

 

 

 

 

A

 

 

 

 

 

 

 

 

 

y

 

dA b dy;

h

 

 

 

 

 

 

 

c

 

zc

I y

2

dA;

 

 

 

 

z

 

 

 

 

 

A

 

 

 

 

 

dA h dz;

 

dz

z

 

 

 

 

 

 

b/2

 

 

 

 

 

 

b

 

 

 

 

Момент инерции относительно оси z:

h

h

 

 

 

 

 

 

 

 

 

 

 

 

b h3

 

 

 

 

2

 

 

b y3

2

 

 

 

b h3

 

 

b h3

Iz y2 b dy b y2 dy

 

 

 

 

 

 

 

 

 

 

 

 

 

;

3

 

 

 

 

24

24

12

A

 

 

h

 

 

 

h

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

2

 

Аналогично получают момент инерции относительно оси y:

 

 

b

 

 

 

 

 

b

 

2

 

 

h z

3

 

2

 

I y z2 h dz h z2 dz

 

 

 

 

 

 

 

 

A

 

 

b

3

 

 

 

b

 

 

 

 

 

 

 

 

 

 

2

2

 

 

h b3

 

 

h b3

 

h b3

 

 

 

 

 

 

 

 

;

24

24

12

 

 

 

 

 

 

В куб вводится сторона прямоугольника, перпендикулярная оси относительно которой определяется момент инерции.

Момент сопротивления относительно оси z:

Wz yIz ,

max

где ymax h2 – координата точки, максимально удаленной от оси z.

Wz

 

I

z

 

b h3

2

 

b h2

 

 

 

;

 

 

 

 

 

 

 

 

 

 

 

ymax

 

12 h

 

6

 

Момент сопротивления относительно оси y:

Wy zI y ,

max

где zmax b2 – координата точки, максимально удаленной от оси y.

 

 

 

I y

 

h b3 2

 

h b2

W

y

 

 

 

;

zmax

12 b

6

 

 

 

 

 

 

 

 

 

 

 

2. Круг:

R

D

yc

dA

 

 

dρ

I p ρ2dA;

 

ρ

A

 

 

c

 

dA 2 π ρ dρ;

 

zc

Полярный момент инерции:

R

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

ρ

4

 

R

 

 

π R

4

 

 

 

π d

4

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

I p 2 π ρ3 dρ 2 π

 

 

 

 

 

 

 

 

 

 

 

;

 

 

4

 

 

 

2

 

 

 

 

 

 

32

 

 

0

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

0

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Осевые моменты инерции:

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

I p I y Iz ;

 

 

 

 

 

I y Iz ;

 

 

 

 

 

 

 

 

 

 

 

 

 

I

 

 

 

D4

; I

 

 

I

 

 

 

D4

;

 

 

 

 

 

 

 

 

 

y

64

 

z

y

 

 

64

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Моменты сопротивления:

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

– осевые:

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

W

 

 

I

z

 

 

 

π D3

;

 

W

 

 

 

W

 

π D3

;

 

 

 

 

z

 

D

 

 

 

 

 

32

 

 

 

 

 

 

y

 

 

 

z

 

 

 

32

 

 

 

 

 

 

 

 

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

– полярный:

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

W

 

 

 

 

I p

 

 

 

D3

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

p

D

 

 

 

 

 

 

 

16

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

3. Половина круга:

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

I

 

 

D

4

;

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

y

 

 

 

128

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

I

z

0,11 R4 ;

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

4R/(3 π )

R

yc

c

zc

4. Прямоугольный треугольник:

 

 

yc

 

h

h/3

c

zc

 

 

 

b/3

 

 

 

b

I

 

 

b h3

z

 

 

;

36

 

 

 

 

 

 

 

 

 

I

 

 

 

h b3

y

 

 

;

 

 

 

36

 

 

 

 

 

 

 

5. Равнобедренный треугольник:

yc

h

h/3

 

 

 

 

 

c zc

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

b/2

b

Iz b h3 ; 36

I y h b3 ; 48

Все выше приведенные выражения справедливы для главных центральных

осей.

Моменты инерции более сложных фигур приведены в специальной литературе (Справочники машиностроителя, Справочники по сопротивлению материалов).

Помимо выше перечисленных простых форм поперечного сечения (круг, прямоугольник и др.) в строительстве и машиностроении широко используют при конструировании балок стандартные гостированные профили.

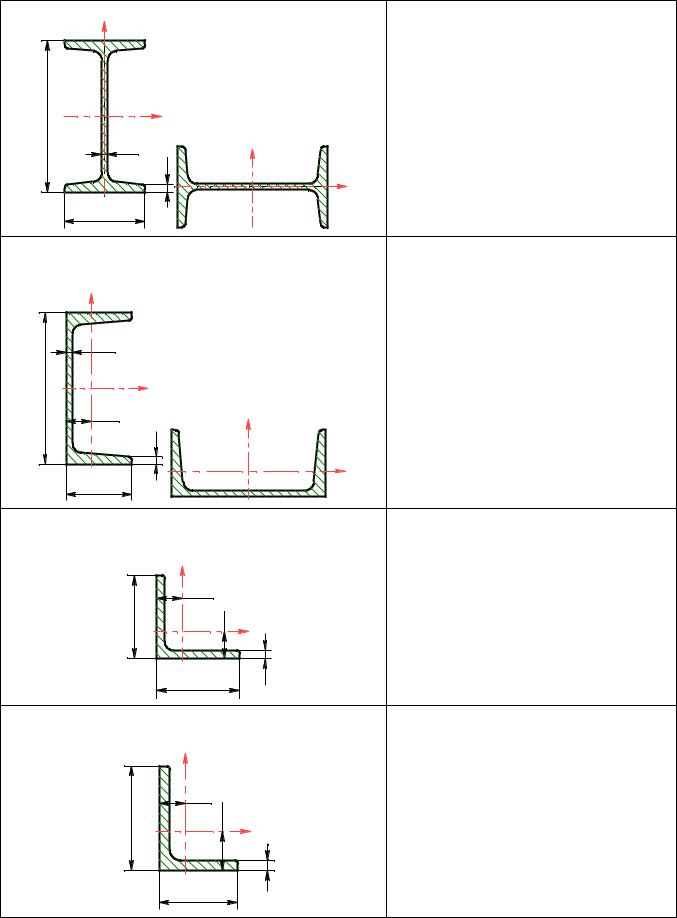
1. Двутавр:

Пример обозначения:

ГОСТ 8239–97.

№ (см)

yc

 

c

zc

h

t

b

yc

 

c

zc

2. Швеллер:

 

yc

 

(см)

h

 

c

zc

№

z0

 

 

 

 

 

t

 

b

 

yc

 

c

zc

3. Уголок равнополочный (равнобокий):

 

yc

 

 

y0

 

b

0

zc

c y

 

b

t

4. Уголок неравнополочный:

 

yc

 

B

z0

zc

c y

 

0

 

 

b

t

№ 18 (18 см – высота);

Выпускаются промышленностью:

№№10÷60.

№18а – усиленный.

Пример обозначения: ГОСТ 8240–97.

№ 18 (18 см – высота);

Выпускаются промышленностью: №№ 5÷50.

Пример обозначения: ГОСТ 8509–86.

№ b t (b – высота полки; t – толщина полки);

b B;

Пример обозначения: ГОСТ 8510–86.

№ B b t (B, b – длины полок; t – толщина полок);

Все геометрические характеристики стандартных сечений (площадь, моменты инерции и др.) приведены в справочной литературе.

Если сечение повернуто на угол 90 , то индекс оси в данных из справочной литературы нужно изменить с учетом обозначения осей на расчетной схеме.

8.4. Центробежный момент инерции

Izy z y dA .

A

Если фигура имеет хотя бы одну ось симметрии, то ее собственный центробежный момент равен нулю. Если фигура не имеет осей симметрии, то понятие центробежный момент используется для определения положения главных цен-

тральных осей.

8.5. Зависимости между моментами инерции при параллельном переносе осей

Осевые моменты инерции относительно осей y1 z1:

Iz1 y12 dA y a 2 dA y2 dA 2 y a dA a2 dA;

A A A A A

y2 dA Iz ;

A

2 y a dA 2 a Sz 0 y dA;

A A

Для I y1 преобразования выполняются аналогично.

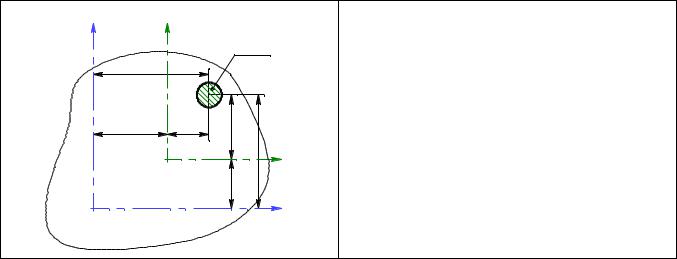
y1

y

 

 

 

Моменты инерции Iz, Iy известны;

 

dA

 

Смещения b и a осей y1 z1 относи-

 

z1

 

 

 

 

 

 

тельно осей y и z известны.

 

 

 

 

 

 

 

 

 

 

Тогда справедливо, что:

b

z

y

1

z

y1 y a;

 

 

 

y

 

 

0

a

 

 

z1 z b;

 

 

 

 

 

01

 

 

 

z1

 

 

 

 

 

 

Центробежный момент инерции в осях y1 z1:

Iz1 y1 z1 y1dA (z b) ( y a)dA (z y z a b y a b)dA;

A

A

 

A

 

Iz Iz 2 a Sz a2 A;

 

1

 

2

 

 

 

 

 

 

I y

I y 2 b Sy b

 

A;

(*) ,

1

Izy a Sy b Sz a b A;

Iz y

1 1

 

 

 

 

 

 

 

 

Уравнения (*) называется формулами параллельного переноса осей.

Чем дальше ось расположена от центра тяжести, тем больше величина осевых и центробежного моментов инерции.

В случае перехода от центральных осей (z, y) к произвольным (y1, z1), формулы переноса существенно упрощаются, так как статические моменты относительно центральных осей равны нулю:

Iz Iz a2 A;

 

1

 

 

 

 

 

 

I y

 

I y b2 A;

(**)

1

 

Izy a b A;

Iz y

1

1

 

 

 

 

 

Для сложных фигур моменты инерции относительно центральных осей всего сечения рассчитывают как сумму осевых моментов каждой из простейших фигур с учетом их смещения относительно центра тяжести всего сечения:

Iz

c

(Iz

ai

2 A );

 

i

 

i

 

 

 

(I y

bi

 

 

I y

2 Ai );

 

c

i

 

 

 

где I zi , I yi – осевые моменты инерции простых фигур сложного сечения, м4; Ai – площади поперечных сечений простых фигур, м2;

ai yi yc – смещение центров тяжести простейших фигур относительно

центра тяжести всего сечения вдоль оси y;

bi zi zc – смещение центров тяжести простейших фигур относительно

центра тяжести всего сечения вдоль оси z;

yi , zi – координаты центров тяжести простейших фигур относительно

начальных осей;

yc , zc – координаты центра тяжести всего сечения относительно начальных

осей;

8.6. Зависимость между моментами инерции при повороте осей.

Пусть известны моменты инерции фигуры относительно осей z и y. Рассмотрим ее моменты инерции в системе осей u и v, повернутых относительно осей z и y на угол .

y

 

z

 

 

 

 

 

 

dA

 

 

v

u

 

 

 

 

 

 

 

K

v

u

 

 

 

α

 

 

 

y

 

 

 

 

α

B

C

 

 

 

 

 

 

 

 

 

 

D

 

 

O

 

E

 

z

 

 

 

 

 

Iz, Iy, Izy, α – известны.

Пересчет положения в различных системах координат:

u OC OB BC

KE sin(α) OE cos(α)

y sin(α) z cos(α);

vKC KD CD

KE cos(α) OE sin(α)

y cos(α) z sin(α);

Моменты инерции в координатной системе uv:

Iu v2 dA;

Iv u2 dA;

A

A

Iuv u v dA;

A

Моменты инерции относительно осей u и v, через координаты z и y:

 

 

 

Iu

y cos(α) z sin(α) 2

dA

 

 

 

 

 

 

 

A

 

 

 

 

 

 

y2

cos2 (α) dA 2 y z sin(α) cos(α) dA z2

sin2 (α) dA;

 

A

 

 

 

 

A

 

 

 

A

 

 

Или:

 

 

 

 

 

 

 

 

 

 

 

 

I

u

I

z

cos2 (α) I

y

sin2 (α) I

zy

sin(2 α);

(1)

 

 

 

 

 

 

 

 

 

 

 

Iv

z cos(α) y sin(α) 2

dA

 

 

 

 

 

 

 

A

 

 

 

 

 

 

z2

cos2 (α) dA 2 y z cos(α) sin(α) dA y2

sin2 (α) dA;

 

A

 

 

 

 

A

 

 

 

A

 

 

Или:

 

 

 

 

 

 

 

 

 

 

 

 

I

v

I

y

cos2 (α) I

z

sin2 (α) I

zy

sin(2 α);

(2)

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Центробежный момент инерции:

Iuv y sin(α) z cos(α) y cos(α) z sin(α) dA;

A

I

 

 

I

z

sin(2α)

 

I y

sin(2α)

I

 

cos(2α);

uv

 

 

2

 

2

zy

 

 

 

 

 

 

 

(3)

 

 

 

 

 

 

 

 

 

Сложив уравнения (1) и (2), получим:

Iu Iv Iz (sin2 (α) cos2 (α)) I y (cos2 (α) sin2 (α))Izy (sin(2 α) sin(2 α)) Iz I y ;

Iu Iv Iz I y const; – сумма осевых моментов относительно двух взаимно перпендикулярных осей не зависит от угла поворота.

8.7. Главные оси сечения.

Полученные выражения для моментов инерции свидетельствуют, что при повороте случайных центральных осей моменты инерции для них будут изменяться. При этом относительно одной оси моменты инерции будет, например, возрастать, относительно другой, соответственно, снижаться.

Таким образом, можно найти положение осей u, v или угол α, при котором момент инерции относительно одной оси примет максимальное значение, относительно второй – минимальное. Полученные оси будут являться главными центральными осями сечения, а моменты инерции относительно главных осей называются главными моментами инерции.

Для определения значений экстремальных моментов инерции продифференцируем выражение (1) по углу :

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
Помощь Обратная связь Вопросы и предложения Пользовательское соглашение Политика конфиденциальности