
Спиглазов_Механика материалов для з.о
..pdf
3. Понятие о напряжениях
3.1. Общие сведения о напряжениях.
Внутренние силы непрерывно распределены по сечению тела, причем в общем случае их величина и направление в отдельных точках сечения различны. Для того чтобы оценить интенсивность внутренних сил в определенной точке, вводится понятие напряжения.
Напряжение – это мера интенсивности внутренних сил, либо количества сил на единицу площади.
Рассмотрим произвольное тело, нагруженное внешними силами.
F1 |
y |
R |
F2 |
B |
|
dA |
x |
Рис. 2.5. Равнодействующая ВСФ в точке
В окрестности произвольной точки В выделим площадку dA. Действующая по dA внутренняя сила имеет равнодействующую R. За среднее напряжение в точке B примем отношение:
pср dAR .
За полное напряжение в точке В примем lim:
pВ lim R .
dA 0 dA
Напряжение – внутренняя сила, приходящаяся на единицу площади в данной точке конкретного сечения.
Размерность напряжений: p 1 мH2 1 Па .
В технических расчетах для упрощения записи перед единицей измерения используют приставки, обозначающие десять в степени:
1кПа = 1∙103 Па; 1МПа = 1∙106 Па; 1ГПа = 1∙109 Па.
3.2. Составляющие полного напряжения.
Полное напряжение обычно раскладывают на составляющие:
–нормальное напряжение – проекция полного напряжения на нормаль к сечению, обозначается греческой буквой (сигма);
–касательное напряжение – проекция полного напряжения, лежащая в
плоскости сечения, обозначается греческой буквой (тау). Для упрощения пони-
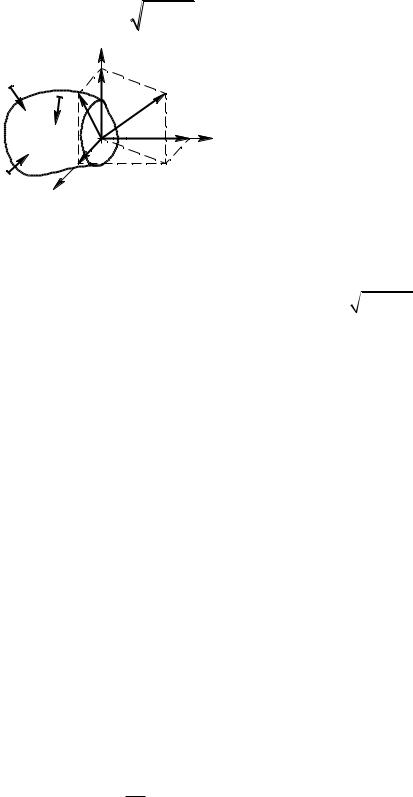
мания касательное напряжение раскладывают на две составляющие в виде про- |
||||
екций на главные оси сечения – x и y: τ |
τ2x τ2y . |
|||
|
|
y |
|
|
F1 |
py=τy |
|
|
|
|
|
|
|
|
F2 |
|
τ |
p |
p =σ |
|
|
|
x |
|
|
|
|
|
x(n) |
F3 |
z |
pz=τz |
|
|
|
|
|
||
Рис. 2.6. Компоненты полного напряжения |
||||
Напряженное состояние – совокупность напряжений для множества площадок, проходящих через одну и ту же точку.
Полное напряжение в точке можно определить по формуле: p 
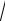 σ2 τ2 .
σ2 τ2 .
3.3. Связь напряжений с ВСФ
N σx dA; |
M y σx z dA; |
A |
A |
Qy τ y dA; |
M z σx y dA; |
A |
A |
Qz τz dA; |
M x τ ρ dA; |
A |
A |
3.4. Перемещения и деформации.
Под действием любых типов нагрузок все тела изменяют свои размеры и форму, т.е. деформируются. Деформации по типу изменения геометрии бывают:
–линейные – изменение линейных размеров тела;
–угловые – изменение угловых размеров тела.
Экспериментально установлено, что для каждого материала ε//  ε =const .
ε =const .
Отношение между относительными продольной и поперечной деформациями взятое с противоположным знаком называется коэффициентом Пуассона (безразмерная величина):
με .
ε/ /
Значение µ характеризует упругие свойства материала и называется упругой постоянной материала. Значение µ определяется экспериментально, для изотропных материалов 0 μ 0,5 .
|
Таблица |
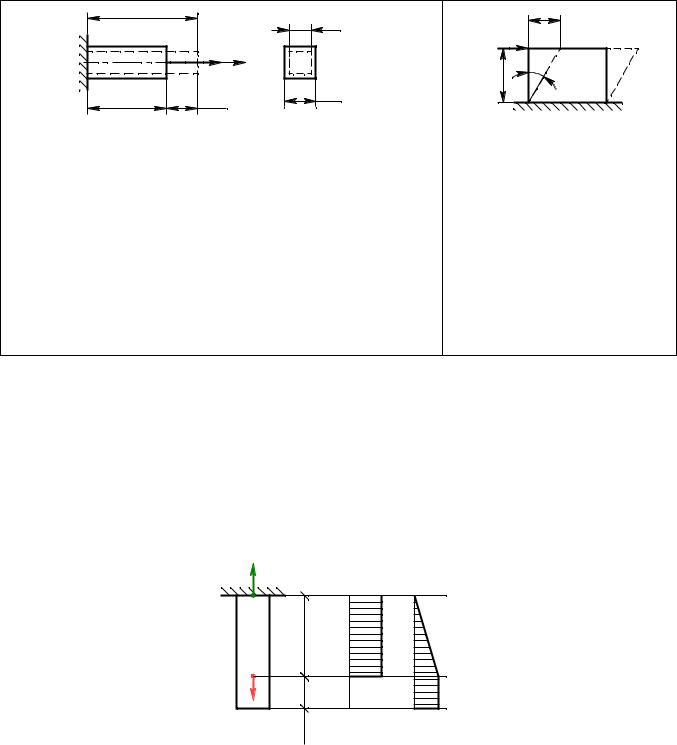
Виды деформаций и их определение |
|
линейная деформация |
угловая деформация |
|
l |
|
pa0 |
|
|
c |
|
|
|
F |
B |
B/ |
|
|
F |
x |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
a |
|
γ |
l0 |
l |
|
pa |
|
|
|
l l l0 |
– абсолютная продольная деформация, м; |
с – абсолютная деформа- |
||||||||
a a0 a – абсолютная поперечная деформация, м; |
ция сдвига |
|||||||||
ε |
|
|
l l0 |
(100%) l (100%) |
– относительная про- |
γ tg(γ) |
c |
– угол сдвига |
||
// |
|
|
|
|||||||
|
|
|
l0 |
|
l0 |
|
|
a |
||
|
|
|
|
|
|
|
||||
дольная деформация (в долях или %), значение не |
(относительный сдвиг) |
|||||||||
ограничено; |
|
|
|
|
||||||
ε |
|
|
a0 a |
(100%) a (100%) |
– относительная по- |
|
|
|
||
|
|
|
|
|
||||||
|
|
|
a0 |
|
a0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
перечная деформация (в долях или %), не может быть более 100%.
Любое сложное деформирование может быть разложено на три линейных и три угловых (по направлением осей пространственной системы координат).
Различают деформации упругие, исчезающие после снятия нагрузки, и остаточные – не исчезающие после снятия нагрузки.
Свойство материалов приобретать остаточные деформации называется пла-
стичностью.
Перемещения точек являются следствием деформаций.
Перемещение точек – кратчайшее расстояние между крайними положениями точек до и после деформирования в направлении приложения нагрузки.
R |
|
"-" 0 "+" |
|
|
|
C |
деформация |
эп. δ |
|
||
|
|
|
B |
|
|
F |
|
эп. N |
A |
. |
|
перем |
|
|
|
|
|
Рис. 2.7. Деформации и перемещение |
||
Участок ВС деформируется, его точки перемещаются на разные расстояния (величина перемещения возрастает по мере удаления от защемления). Участок АВ не деформируется – все точки перемещаются на одинаковую величину.
3.5.Вопросы для самоконтроля
1.Общие сведения о напряжениях.
1.1.Понятие напряжения.
1.2.Единицы измерения.
2.Составляющие полного напряжения.
2.1.Понятие нормальных напряжений.
2.2.Понятие касательных напряжений, составляющие касательных напряжений.
2.3.Напряженное состояние.
2.4.Полное напряжение.
3.Связь напряжений с ВСФ.
4.Перемещения и деформации.
4.1.Деформации по типу изменения геометрии.
4.2.Понятие абсолютной и относительной деформации.
4.3.Определение деформаций.
4.4.Коэффициент Пуассона, диапазон значений.
4.5.Деформации по способу воздействия на материал.
4.6.Понятие упругих и остаточных деформаций.
4.7.Понятие перемещения точек.
К содержанию
4. Осевое растяжение и сжатие.
Растяжение или сжатие это такой вид напряженного состояния, при котором в поперечных сечениях бруса действует только один вид ВСФ – продольная сила N (нормальная к сечению).
4.1. Напряжения при растяжении (сжатии).
Рассмотрим прямолинейный брус с постоянным по длине поперечным сечением площадью А, нагруженный растягивающими силами.
Нанесем на боковую поверхность бруса прямоугольную сетку линий. На торцах бруса равномерно приложим нагрузку с равнодействующей силой F. Очевидно, что после деформирования линии сетки сместятся относительно серединного сечения А–А в обе стороны вдоль оси бруса. При этом данные линии останутся прямыми и вертикальными. На основании этого сделано предположение, что поперечные сечения бруса плоские и нормальные к его продольной оси останутся такими и после деформирования (гипотеза Бернулли).
Исходя из гипотезы Бернулли предполагается, что нормальные напряжения распределены по площади сечения равномерно, т.е. σx σ const .
F |
F |
|
N F , |
|
|
||
А |
N σdA, |
|
|||
|
A |
|
|
|
|
F |
F |
|
|
N |
|
|
σ σ |
x |
, |
||
|
|
|
A |
|
|
|
|
|
|
|
|
А
F |
N x |
|

 σx
σx
Рис. 3.1. Осевое растяжение
где N – продольный силовой фактор;
А – площадь поперечного сечения.
Для вычисления напряжений при растяжении (сжатии) необходимо внутреннюю продольную силу, взятую с соответствующей эпюры, разделить на площадь поперечного сечения.
4.2. Расчет на прочность при растяжении (сжатии).
4.2.1. Условие прочности.
Безопасность работы любой конструкции может быть обеспечена только в том случае, когда максимальные напряжения в любом ее элементе не превышают некоторого допускаемого значения [ ] – условие прочности:
σmax [σ]
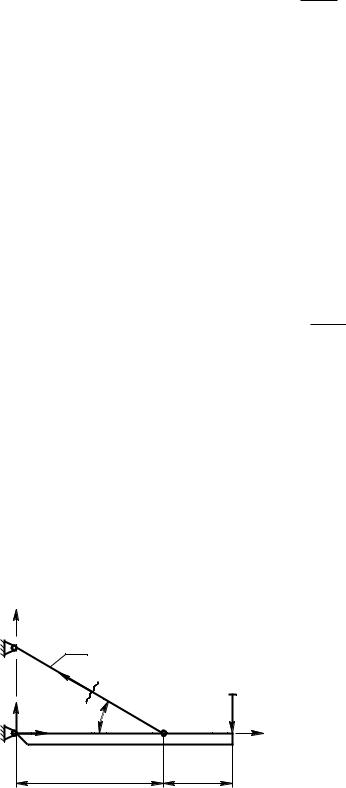
Данное условие прочности справедливо при многих видах нагружения, в том числе и при растяжении (сжатии).
Допускаемые напряжения [ ] для любых материалов определяются по результатам экспериментальных исследований и назначения конструкции.
При растяжении (сжатии) условие прочности имеет вид:
σmax Nmax [σ],
A
где Nmax – наибольшее значение продольного силового фактора, на участке стержня с площадью А (берут только из эпюры);
4.2.2. Варианты использования условия прочности.
Условие прочности для любых видов нагружения позволяет решать ряд задач механики материалов и конструкций. Для растяжения (сжатия):
1. Проверочные расчеты – позволяет определить выполнение условия безопасной работы конструкции с известными размерами (площадь А) при известных
нагрузках (Nmax = f(Fe));
2. Конструкционные расчеты – определение размеров элементов (площади А) по заданным нагрузкам (Nmax = f(Fe)) при известном значении свойства материала ([ ]):
A Nmax .
[σ]
3. Монтажные расчеты (несущая способность конструкции) – это определение допускаемой нагрузки ([F] F f (N) ) при известных размерах конструк-
ции (площадь А) и свойствах материла ([ ]):
N [N] [σ] A [F] F f (N) ,
где значение F определяется из уравнений равновесия статики при рассчитанном из условия прочности N .
4.2.3. Пример расчета конструкции на прочность.
Для конструкции, показанной на рисунке определить величину допускаемой силы из условия прочности стержня CD. Брус ВК жесткий, недеформируемый.
y |
|
|
|
|
|
|
|
D |
ACD |
|
|
|
Дано: |
|
|
NCD |
|
|
|
= 30 ; |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
ACD = 3 см ; |
YB |
|
|
|
|
F |
[ ] = 160 МПа; |
XB |
α |
C |
K |
|
||
|
|
|
Определить: |
|||
|
|
|
|
|
x |
|
B |
|
|
|
|
[F] – ? |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
2 м |
|
1 м |
|
|
|
|
|
|
|
|
Решение. |
1.Обозначим систему координат xy с началом в точке В;
2.Рассечем стержень. Отбросим ту его часть, которая не связана с элементами, воспринимающими внешнюю нагрузку (F);

3.Укажем вектора внутренних усилий в стержнях (NCD) и реакции в опорах (YB, XB);
4.Составим для плоской произвольной системы сил уравнения равновесия статики:
Fx 0; X B NCD cos(α) 0;
2. Fy 0; |
YB NCD sin(α) F 0; |
3. M B (Fi ) 0; |
NCD sin(α) 2 F 3 0; |
Для расчетов на прочность имеет значение только внутреннее усилие в стержне – которое можно найти из третьего уравнения равновесия в виде функции от внешней силы F:
N |
|
|
|
3 |
F |
3 |
F 3 F |
F |
NCD |
. |
CD |
|
sin(α) |
2 sin(30 ) |
|
||||||
|
2 |
|
|
3 |
|
|||||
|
|
|
|
|
||||||
5. Из условия прочности определим максимально возможное значение N для стержня.
σ |
|
|
|
Nmax |
[σ] |
|
|
|
|
max |
|
|
|
||||||
|
|
|
A |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
N |
CD |
N |
max |
[ ] A 160 106 |
3 10 4 |
48 103 H 48 кН. |
|||
|
|
|
|
|
|
|
|
||
6. Определим допускаемую нагрузку F. |
|
|
|||||||
[F ] F |
|
Nmax |
|
48 |
16 кН . |
|
|
||||
max |
3 |
3 |
|
||
|
|
||||
4.3. Деформация при растяжении (сжатии).
При осевом растяжении (сжатии) в брусе возникает только линейная деформация (продольная и поперечная).
4.3.1. Закон Гука
На основании обобщения экспериментальных данных в 1776 г. Ф. Гук сделал обобщение, названное законом Гука:
– в определенных пределах между нагрузкой и деформацией существует прямо-пропорциональная зависимость.
В относительных единицах данную зависимость можно представить в виде: σ E ε ,
где E – коэффициент пропорциональности между нагрузкой и деформацией,
называемый модулем упругости первого рода или модулем Юнга.
Модуль Юнга этот упругая характеристика материала, определяемая экспериментально – характеризует способность материала упруго сопротивляется деформированию.
В абсолютных единицах закон Гука представлен выражением:
N |
E |
l |
|
l |
N l |
, |
|
A |
l |
E A |
|||||
|
|
|
|
где произведение EA – жесткость стержня при растяжении.
Чем выше жесткость конструкции, тем меньше величина его деформации при одной и той же нагрузке. Жесткость можно увеличить за счет выбора материала с большим значением Е или увеличив размеры сечения (площадь А).
Жесткость стержня – способность элемента сопротивляться деформированию с учетом свойств материала и его геометрии. Часто жесткость обозначают отдельной величиной:
D E A ,
Данное соотношение справедливо в случае если стержень изготовлен из однородного изотропного материала с Е = const, имеет постоянное поперечное сечение А = const в пределах длины l. Если стержень имеет ступенчатое строение, тоl рассчитывают для каждой i-ой ступени отдельно:
li Ni li ,
E Ai
где li – длина участка, для которого Ni и Ai постоянны.
Полное удлинение стержня рассчитывается по формуле: l li . Для
i
консольных стержней перемещение точки равно сумме удлинений участков между этой точкой и защемлением. При расчете учитывают знак Ni и, следовательно,li – знак «+» означает, что участок удлиняется, знак «–» – укорачивается.
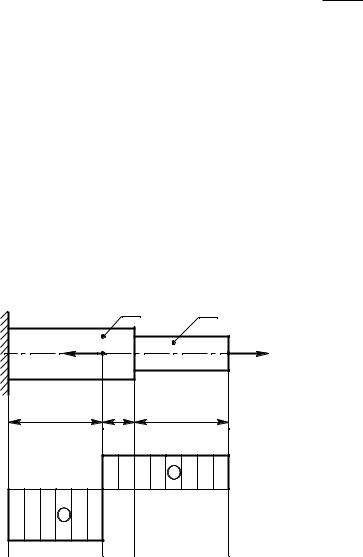
4.3.2. Пример определения деформаций.
Стержень разбивают на три участка:
Уч. 1 (ВС):
|
|
A2 |
A1 |
|
F2 |
|
F1 |
E |
D |
C |
B |
c |
b |
|
a |
|
|
|
N=F1 |
"+" |
|
|
+ |
|
|
|
|
0 |
|
|
|
"-" |
- |
|
|
N=F1-F2 |
|
|
|
l |
|
a , N |
|
N F |
, A A ; l |
|
|
|
NBC lBC |
; |
|||||
BC |
BC |
BC |
|
||||||||||||
|
|
|
1 |
BC |
1 |
|
|
E ABC |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Уч. 2 (СD): |
|
|
|
|
|
|
|
|
|
|
|
||||
l b , N |
|
N F |
, A A |
; l |
|
|
NCD lCD |
; |
|
||||||
CD |
|
|
|
||||||||||||
CD |
|
|
1 |
CD 2 |
CD |
|
|
E ACD |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Уч. 2 (DE): |
|
|
|
|
|
|
|
|
|
|
|
||||
lDE c , |
|
|
NDE N F1 F2 , |
|
|
|
|
ADE A2 ; |
|||||||
lDE |
NDE lDE |
; |
|
|
|
|
|
|
|
|
|
||||
E ADE
Полное удлинение стержня:
l lBC lCD lDE ;
Перемещение точки С:
δC lCD lDE ;
Модуль Юнга определяется экспериментально. Некоторые данные приведены в таблице 3.
Таблица 3
Значения модуля Юнга
Материал |
Модуль Юнга |
|
(E, ГПа) |
Сталь |
(1,98–2,2)∙105 МПа 2∙105 МПа = 200 ГПа |
Алюминий |
70 ГПа |
Медь |
120 ГПа |
Древесина |
10 ГПа |
Полимеры |
0,8–3 ГПа |
Композиты |
2–50 ГПа |
4.4. Расчет на жесткость при растяжении (сжатии).
По аналогии с расчетами на прочность, безопасность работы любой конструкции может быть связана с допускаемой величиной деформации [ε] и допускаемым перемещением (смещением) точек [δ]. Условие жесткости можно записать в виде:
εmax [ε] или δmax [δ]
Данное условие жесткости справедливо при многих видах нагружения, в том числе и при растяжении (сжатии).
Допускаемые деформации [ε] для любых материалов определяются по результатам экспериментальных исследований и назначения конструкции, допускаемые перемещения [δ] задают по конструктивным соображениям.
При продольном растяжении (сжатии) условие жесткости имеет вид:
εmax |
|
σmax |
|
Nmax |
[ε] или δmax li |
|
Ni |
li |
[δ] , |
|
E A |
E A |
|||||||
|
|
E |
i |
i |
|
||||
|
|
|
|
|
|
i |
|
||
где Nmax – наибольшее значение нармальных напряжений по длине стержня, на
участке стержня с площадью А (берут только из эпюры).
Если точка непосредственно не связана с деформируемым элементом, то ее перемещение определяется геометрической связью между жесткими и деформируемыми элементами согласно определенных правил и допущений.
4.4.1. Правила построения деформированной системы.
Правила справедливы только для случая малых деформаций.
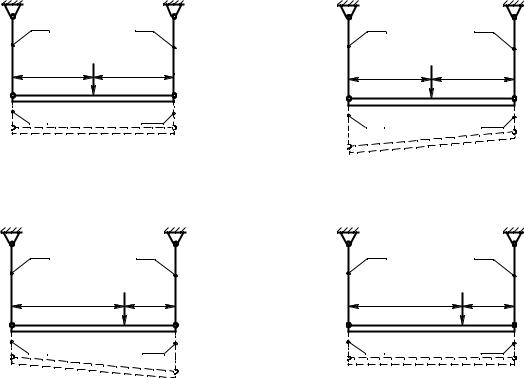
1.Закон перемещения определяется подвижным или неподвижным жестким элементом (шарнир, жесткий брус) относительно точки его крепления (рис. 3.2. – д, е, и, к) или из баланса жесткости стержней (рис. 3.2. – а, б, в, г, ж, з) в направлении главного вектора внешних сил.
2.Вследствие малости деформаций (перемещений) по отношению к размерам конструкции все точки, принадлежащие жесткому брусу, смещаются по перпендикулярам к их исходному положению. При этом жесткий брус может совершать вращательное (рис. 3.2. – д, е, к), линейное (рис. 3.2. – а, г, ж, и) или плоскопараллельное движение (рис. 3.2. – б, в). Характер движения зависит от способа крепления бруса.
3.Смещение подвижного шарнира возможно только в направлении степени свободы (рис. 3.2. – и);
4.Смещение внутреннего шарнира обусловлено балансом жесткости стержней или траекторией перемещения жестких элементов (согласно п.2.) (рис. 3.2. – и);
5.Связь перемещений точек, принадлежащих жесткому брусу, определяется из подобия треугольников, две стороны которых являются отрезками бруса в крайних положениях (деформированном и недеформированном), а третья искомыми перемещениями точек.
6.Деформации стержней отображают как разность между большей длиной
именьшей длиной стержня в исходном и деформированном состоянии. В случае если стержни расположены под углом – предварительно выполняют проецирование стержня меньшей длины на стержень большей длины – удлинение определяется как разность большей длины и проекции меньшей длины.
7.Удлинения стержней геометрически связаны с перемещениями точек их крепления к шарнирам или жестким брусьям. Как правило, точки крепления в крайних положениях обуславливают начальную и конечную длину стержня. Связь между удлинением стержня и перемещением точек обусловлена геометрической зависимостью. Если ось стержня не изменяет своей ориентации, то его удлинение (укорочение) равно смещению точек. При отклонении оси стержня его удлинение (укорочение) и перемещение точек соотносятся между собой как катет
игипотенуза прямоугольного треугольника.
1 |
|
2 |
|
l |
F |
l |
|
|
|
||
K |
|
|
B |
l1 |
|
l2 |
B' |
K' |
|
|
D1 D2 ; N1 N2 ; KB / /K ' B' ;
KK ' BB' ;
l1 KK ' ; l2 BB '; l1 l2
а)
|
1 |
2 |
|
|
2l |
F l |
|
K |
|
|
B |
K' |
l1 |
l2 |
B' |
|
|
||
|
|
|
D1 D2 ; N1 N2 ; KK ' BB ';
l1 KK ' ; l2 BB ' ; l1 l2
в)
1 |
|
2 |
|
l |
F |
l |
|
|
|
||
K |
|
|
B |
l1 |
|
l2 |
B' |
K' |
|
|
|
|
|
|
D1 D2 ; N1 N2 ; KK ' BB' ;
l1 KK ' ; l2 BB '; l1 l2
|
б) |
|
|
1 |
|
2 |
|
2l |
F |
l |
|
|
|
||
K |
|
|
B |
l1 |
|
l2 |
B' |
K' |
|
|
2 D1 D2 ; 2 N1 N2 ; KB / /K ' B ' ; KK ' BB ' ;
l1 KK ' ; l2 BB ' ; l1 l2
г)
