
Диплом / suslov_ibragimov_ekonometrika
.pdf
152 |
Глава4.Введение в анализ связей |
данный коэффициент выражает скорееÇалгебраическоеÈкачество построенного уравнения регрессии.
Показатель статистической значимости оцененного уравнения дает статистика ФишераÑкак и для регрессии,построенной по данным совместного распределения признаков.В данном случае остаточная дисперсия имеет N − 2 степени свободы,а объясненнаяÑодну степень свободы(доказательство этого факта дается воIIчасти книги):
F c = |
sq21 (N − 2) |
= |
R2 (N − 2) |
. |
|
||||
|
se21 |
(1 − R2) |
||
Если переменные не зависят друг от друга,т.е. α12 = 0 (нулевая гипотеза), то эта статистика имеет распределение Фишера с одной степенью свободы в числителеи N −2 степенями свободы взнаменателе.Логикаиспользования этойстатистики описана выше.Статистическая зна чимость(качество)полученного уравнениятемвыше,чемнижезначениепоказателя pv длярасчетногозначенияданной статистики F c .
Оценкипараметров α12, β1 иостатков εi1 можнополучитьиначе,изрегрессии x2 по x1:
xöi2 = a21xöi1 + ei2, i = 1, . . . , N .
В соответствии с(4.26)оценка углового коэффициента получается делением ковариациипеременных,стоящихвлевойиправойчастяхуравнения,надисперсию факторной переменной,стоящей в правой части уравнения:
a21 = m21 . m11
1 |
|
1 |
|
|
|
|
|
|
|
|||
Поскольку xöi1 = |
|
xöi2 − |
|
ei2 |
, |
|
|
|
|
|||
a21 |
a21 |
|
|
|
||||||||
|
a12 (2) = |
1 |
|
= |
m11 |
, |
(4.32) |
|||||
|
a21 |
|
||||||||||
|
|
|
|
|
|
m21 |
|
|||||
|
b1 (2) = xø1 − a12 (2) xø2, |
|
||||||||||
|
ei1 (2) = a12 (2) ei2, |
|
i = 1, . . . , N. |
|
||||||||
ЭтоÑновые оценкипараметров.Легкоубедиться втом,что |
a12 (2) совпадает |
|||||||||||
с a12 (а вслед за ним b1 (2) |
совпадает с |
|
b1 и ei1 (2) Ñ с |
ei1)тогда и только |
||||||||
тогда,когда коэффициент корреляции r12 |
равен единице,т.е.зависимость имеет |
|||||||||||
функциональный характер и все остатки равны нулю. |
|
|||||||||||
При оценке параметров α12, β1 и остатков ei1 регрессия x1 по x2 иногда называется прямой,регрессия x1 по x2 Ñ обратной.
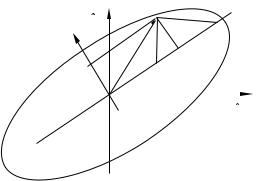
4.2.Регрессионный анализ |
|
|
153 |
A |
|
r |
Нарисунке4.2вплоскости(впро- |
x1 |
|
странстве)переменных x1, x2 при- |
|
C |
|
||
|
|
||
E |
|
менение прямой регрессии означает |
|
|
|
Dминимизацию суммы квадратов рас-
|
F |
|
B |
|
стояний от точек облака наблюдений |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
до линии регрессии,измеренных па- |
|
|
|
0 |
|
x2 |
||
|
|
|
раллельно оси x1.При применении |
|||
|
|
|
|
|||
|
|
|
|
|
||
|
|
|
|
|
обратной регрессии эти |
расстояния |
1 |
|
|
|
|
измеряются параллельно оси x2. |
|
|
|
|
|
|
lr Ñлиния регрессии, |
|
|
|
Рис. 4.2 |
|
|
OA Ñвектор-строка |
i-го на- |
|
|
|
|
блюдения xöi = (öxi1, xöi2), |
|
|
|
|
|
|
|
|
|
AB Ñрасстояние до линии регрессии,измеренное параллельно оси xö1,равное величине ei1,
AC Ñрасстояние,измеренное параллельно оси xö2,равное величине ei2, AD Ñрасстояние,измеренное перпендикулярно линии регрессии,равное ei , OE Ñвектор-строка a! параметров ортогональной регрессии.
Очевидно,чтооценить параметрырегрессииможно,измеряярасстояния до линии регрессии перпендикулярно самой этой линии(на рисункеÑотрезок AD). Такая регрессия называется ортогональной.В уравнении такой регрессии обе переменные остаются в левой части с коэффициентами,сумма квадратов которых должна равняться единице(длина вектор а параметров регрессии должна равняться единице):
a1xöi1 + a2xöi2 = ei , i = 1, . . . , N |
(4.33) |
|
a2 |
+ a2 = 1. |
|
1 |
2 |
|
В матричной форме: |
|
|
|
ö |
(4.34) |
|
X a = e, |
|
|
a!a = 1, |
|
ö |
|
N 2, a Ñвектор- |
где X Ñматрица наблюдений за переменными,размерности |
||
столбец параметров регрессии. |
|
|
Само уравнение регрессии можно записать еще и так: |
|
|
|
xöia = ei , i = 1, . . . , N . |
(4.35) |
Чтобы убедиться в том,что такая регрессия является ортогональной,достаточно вспомнить из линейной алгебры,что скалярное произведение вектора на вектор
154 |
Глава4.Введение в анализ связей |
единичной длины равно длине проекции этого вектора на единичный вектор.В левой части(4.35)как раз и фигурирует такое скалярное произведение.На рисунке вектором параметров a является OE ,проекцией вектора наблюдений OA(öxi) на этот векторÑотрезок OF ,длина которого( xöi a)в точности равна расстоянию от точки облака наблюдений до линии регрессии,измеренному перпендикулярно этой линии( ei ).
Следует иметь в виду,что и вÇобычнойÈрегрессии,в левой части которой остается одна переменная,коэффициент при этой переменной принимается равным единице,т.е.фактически используе тся аналогичное ортогональной регрессии требование:вектор параметров при переменных в левой части уравнения должен иметь единичную длину.
Впротивоположность ортогональнойÇобычныеÈрегрессииназывают простыми.В отечественной литературе простой часто называютÇобычнуюÈрегрессию с одной факторной переменной.А регрессию с несколькими факторными перемен-
ными называют множественной.
Теперь остаточную дисперсию в матричной форме можно записать следующим образом:
|
|
s2 |
= |
1 |
e!e = |
1 |
a!Xö !Xö a = a!M a, |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
e |
|
N |
|
N |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
N |
|
|
|
|
|
m21 |
m22 |
|||
где M = |
1 |
Xö !Xö Ñматрица ковариации переменных,равная |
|
m11 |
m12 |
. |
|||||
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
Для минимизации остаточной дисперсии при ограничении на длину вектора параметров регрессии строится функция Лагранжа:
L (a,λ ) = a!M a − λa!a,
где λ Ñмножитель Лагранжа(оценка ограничения).
Далее находятся производные этой функции по параметрам регрессии,и эти производные приравниваются к нулю.Результат таких операций в матричной форме представляется следующим образом(поскольку M Ñсимметричная матрица:
M ! = M ):
(M − λI ) a = 0. |
(4.36) |
Таким образом,множитель Лагранжа есть собственное число матрицы ковариации M ,а вектор оценок параметров ре грессииÑсоответствующий правый собственный вектор этой матрицы(см.ПриложениеA.1.2).
Матрица M является вещественной,симме тричной и положительно полуопределенной(см.ПриложениеA.1.2).

4.2.Регрессионный анализ |
155 |
Последнеесправедливо,т.к.квадратичнаяформа µ"M µ прилюбомвекторе µ неотрицательна.Действительно,эту квадратичную форму всегда можно представить как
|
|
1 |
ö |
|
|||
сумму квадратов компонент вектора η = |
|
|
|
||||
√ |
|
X µ: |
|
||||
N |
|
||||||
|
|
|
|
|
|
|
|
" |
M µ = |
1 |
" ö " ö |
" |
η " 0. |
||
µ |
N |
µ X X µ = η |
|||||
Из линейной алгебры известно,что все собственные числа такой матрицы вещественны и неотрицательны,следовательно λ неотрицательно.
После умножения обеих частей уравнения(4.36)слева на a! из него следует,
что
s2e = a!M a = λa!a a!=a=1 λ,
т.е.минимизации остаточной дисперсии соответствует поиск минимального собственного числа матрицы ковариации переменных M .Соответствующий этому собственному числу правый собственный вектор этой матрицы есть вектор оценок параметров ортогональной регрессии a (см.ПриложениеA.1.2).Кроме того, в соответствии со свойствами матрицы M ,сумма ее собственных чисел равна сумме ее диагональных элементов(следу матрицы),и,т.к. λ Ñменьшее из двух собственных чисел,то λ < 12 (m11 + m12) (случай двух одинаковых собственных чисел не рассматривается,т.к.он имеет ме сто,когда связь между переменными отсутствует,и m12 = 0).
Оценка свободного члена b,как и прежде,получается из условия прохождения линии регрессии через точку средних: b = xaø ,где xø Ñвектор-строка средних значений переменных.
Расчетное значение xöi дает вектор OD (см.рис. 4.2),который равен разности векторов OA и OF ,т.е. (в матричной форме):
ö c = ö − !
X X ea .
Теперь можно дать еще одну оценку параметров уравнения(4.18):
a12 ( ) = −a2 , a1
b1 ( ) = xø1 − a12 ( ) xø2,
1 ei1 ( ) = a1 ei .
Полученнаяоценкаугловогокоэффициента a12 ( ) лежитмеждуегооценками по прямой и обратной регрессиям.Дейст вительно,из(4.36)следует,что
a |
( |
|
) = |
|
a2 |
= |
m12 |
|
= |
m11 − λ |
. |
|
|
−a1 |
m22 − λ |
||||||||||
12 |
|
|
|
|
m12 |
|||||||

156 |
Глава4.Введение в анализ связей |
90¡
x1  x1
x1
>90¡
x2
kx2
Рис. 4.3
Отсюда,в частности1 |
,следует,что величины |
m11 − λ и m22 − λ имеют один |
||||||||||
знак,и,т.к. |
λ < 2 (m11 |
+ m12),то обе эти величины положительны. |
|
|
|
|||||||
Поэтому,если m12 " 0,то |
|
|
|
|
|
|
||||||
|
|
m11 (4.32) |
|
(4.26) |
m12 |
|
|
|
|
|||
|
|
|
|
= |
a12 (2) > a12 ( ) |
> a12 = |
|
, |
|
|
|
|
|
|
m12 |
m22 |
|
|
|
||||||
а если m12 ! 0,то a12 (2) < a12 ( ) < a12. |
|
|
|
|
|
|
||||||
Понятно,что эти3оценки совпадают тогда и только тогда,когда |
|
2 |
|
|||||||||
λ |
0= se |
1 = 0, |
||||||||||
т.е.зависимость функциональна. |
|
|
|
|||||||||
В действительности любое число,лежащее на отрезке с концами |
a12, a12 (2) |
|||||||||||
(т.е.либо |
[a12, a12 (2)],если |
m12 " 0,либо [a12 (2) , a12],если |
m12 ! 0),может |
|||||||||
являться МНК-оценкой параметра α12,т.е.оценкой этого параметра является
γ1a12 + γ2a12 (2) при любых γ1 и γ2,таких что γ1 " 0, γ2 " 0, γ1 + γ2 = 1. Каждая из этих оценок может быть получена,если расстояния от точек облака
наблюдениядолиниирегрессииизмерятьподопределеннымуглом,чтодостигается с помощью предварительного преобразования в пространстве переменных.
Убедиться в этом можно,рассуждая следующим образом.
Пусть получена оценка углового коэффициента по ортогональной регрессии (рис.4.3,слева).Теперьпроводитсяпреобразованиевпространствепеременных: xö2 умножается на некоторое число k > 1,и снова дается оценка этого коэффициента по ортогональной регрессии(рис. 4.3,справа).После возвращения в исходное пространствополучается новаяоценка угловогокоэффициента,сопоставимая состарой (возвращение в исходное пространство осуществляется умножением оценки коэффициента,полученной в преобразованном пространстве,на число k).
Этот рисунок не вполне корректен,т.к.переход в новое пространство переменных и возвращение в исходное пространствоведет к смещению линии регрессии.Однако
4.2.Регрессионный анализ |
157 |
смысл происходящего он поясняет достаточно наглядно:новая оценка получена так, как будто расстояния от точек облака наблюдений до линии регрессии измеряются под углом,не равным 90◦.Должно быть понятно,что в пределе,при k → ∞, расстояния до линии регрессии будут измеряться параллельно оси xö1 и полученная оценка углового коэффициента совпадет с a12.Наоборот,в пределе при k → 0 эта оценка совпадет с a12 (2).
Выбор оценок параметров регрессии на имеющемся множестве зависит от характера распределения ошибок измерения переменных.ЭтоÑпредмет изучения воIIчасти книги.Пока можно предложить некоторые эмпирические критерии.
Например,следующий.
Общая совокупность(множество наблюдений)делится на две части:обучающую и контрольную.Оценка параметров производится по обучающей совокупности.На контрольной совокупности определяется сумма квадратов отклонений фактических значений переменных от расчетных.Выбирается та оценка,которая дает минимум этой суммы.В заключение выбранную оценку можно дать по всей совокупности.
Рассмотренныйслучайдвух переменныхлегкообобщитьна n переменных(без доказательств:они даются воIIчасти кни ги).Основное уравнение регрессии запи-
сываетсяследующимобразом: x1 = x−1α−1 + β1 + ε1, где x−1 = [x2, . . . , xn] Ñ вектор-строка всех переменных кроме первой,вектор факторных переменных,
α−1 |
= |
|
α12 |
|
... |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
α |
|
|
|
|
1n |
|
|
|
|
|
|
Ñвектор-столбец параметров регрессии при факторных переменных,а в матрич-
ной форме: |
ö |
|
ö |
|
ö |
N × (n − 1) |
||||
|
X1 |
= X−1a−1 |
+ e1,где X−1 Ñматрица размерности |
|||||||
наблюдений за факторными переменными. |
|
|||||||||
По аналогии с(4.21, 4.26): |
|
|||||||||
|
|
|
|
|
|
|
|
|
a−1 = M−−11m−1, |
(4.37) |
|
|
|
|
|
|
|
|
|
b1 = xø1 − xø−1a−1, |
|
где M |
= |
|
1 |
|
Xö |
! |
Xö |
Ñматрица ковариации факторных переменных между со- |
||
|
|
|
||||||||
−1 |
|
|
N |
−1 |
−1 |
|
|
|
||
бой, |
|
|
|
Xö−! 1Xö1 Ñвектор-столбец ковариациифакторных переменных смо- |
||||||
m−1 = |
1 |
|||||||||
N |
||||||||||
делируемой переменной, |
|
|
||||||||

158 Глава4.Введение в анализ связей
ø−1 = 1 1! ö−1 Ñвектор-строка средних значений факторных переменных. x N N X
Расчетные значения моделируемой переменной,т.е.ее математические ожидания,есть
öc = ö
X1 X−1a−1.
Как и в случае двух переменных объясненной дисперсией является дисперсия расчетных значений моделируемой переменной:
|
1 |
a−! 1Xö−! 1Xö−1a−1 |
|
(4.37) |
|
(4.37) |
sq21 = |
|
= a−! 1M−1a−1 |
= |
a−! |
1m−1 = m−! 1M−−11m−1. |
|
N |
(4.38)
Коэффициентмножественнойкорреляции r1,−1 естькоэффициенткорреляции между моделируемой переменной и ее расчетным значением( cov Ñобозначение ковариации):
|
1 |
|
1Xö−! |
1Xö1 = a−! |
(4.38) |
|
|
|
|||
cov (x1c , x1) = |
|
a−! |
1m−1 = |
|
sq21, |
|
|||||
N |
|
|
|||||||||
r1,−1 = |
|
cov (x1c , x1) |
= |
sq21 |
= |
sq1 |
, |
||||
G |
|
sq1s1 |
|
s1 |
|||||||
var (x1c ) var (x1) |
|||||||||||
Коэффициент детерминации,равный квадрату коэффициента множественной корреляции:
s2 R2 = q1 ,
s21
показывает долю объясненной дисперсии в общей.
Если связь отсутствует и α−1 = 0 (нулевая гипотеза),то расчетная статистика Фишера
F c = |
R2 (N − n) |
|
(1 − R2) (n − 1) |
имеет F -распределение с n − 1 степенями свободы в числителе и N − n степенями свободы в знаменателеÑ Fn−1,N −n .Логика использования этой статистики сохраняется прежней.
Прииспользованиивобщемслучаезаписиуравнениярегрессиивформесоскрытым свободным членом
= ÷ ÷ +
X1 X−1a−1 e,

4.2.Регрессионный анализ |
|
|
|
|
|
|
|
|
|
159 |
|||||||||||||
− |
|
Ñматрица [X |
− |
|
1N ] размерности N |
× |
(n +1), a÷ |
− |
|
|
|
b1 |
|
||||||||||
где X÷ |
|
1 |
|
1, |
|
|
1 |
Ñвектор |
a−1 |
, |
|||||||||||||
оператор МНК-оценивания записывается как |
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
a÷−1 = M÷−−11m÷ −1, |
|
|
|
|
|
(4.39) |
|||||
где m÷ |
−1 |
= |
1 |
X÷ |
! |
X , M÷ |
|
= |
1 |
X÷ |
! |
X÷ |
. |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
N |
−1 |
1 |
−1 |
|
N |
−1 |
−1 |
|
|
|
|
|
|
|
|
|
|||||
Достаточнопростыеалгебраическиепреобразованияпоказывают,чтоэтотоператор эквивалентен(4.37).
Полезной является еще одна геометрическая
AиллюстрациярегрессииÑвпространственаблюдений(см.рис. 4.4и4.5).
|
|
|
|
|
|
|
При n = 2 (n Ñколичество переменных), |
|||
|
|
|
|
|
|
|
OA Ñвектор |
xö1, OB Ñвектор |
xö2, OC Ñ |
|
|
|
|
|
|
|
|
вектор проекции |
xö1 на xö2,равный расчетному |
||
O |
|
C |
B |
|||||||
|
значению xöc , C A |
Ñвектор остатков |
e1,так что: |
|||||||
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
1 |
|
|
|
|
Рис. 4.4 |
|
|
xö1 = a12xö2 + e1.Косинус угла между |
OA и OB |
|||||
|
|
|
|
|
|
|
равен коэффициенту корреляции. |
|
||
При n = 3, OA Ñвектор xö1, OB Ñвектор |
|
|
||||||||
xö2, OC Ñвектор |
xö3, OD Ñвектор проекции |
|
A |
|||||||
xö1 на плоскость,определяемую |
xö2 и xö3,равный |
|
|
|||||||
расчетному значению xöc , DA Ñвектор остатков |
F |
|
||||||||
|
|
|
|
|
1 |
|
|
|
|
|
e1, OE Ñвектор проекции xö1c на xö2,равный |
|
C |
||||||||
a12xö2, OF Ñвектор проекции |
xö1c на xö3,равный |
O |
|
|||||||
a13xö3,так что |
xö1 = a12xö2 + a13xö3 + e1.Косинус |
|
||||||||
|
|
|||||||||
угла между OA и плоскостью,определенной |
xö2 |
|
D |
|||||||
и xö3, (т.е.между OA и OD)равен коэффициенту |
E |
|
||||||||
|
|
|||||||||
множественной корреляции. |
|
|
|
|
||||||
Кроме оценки |
a−1 можно получить оценки |
B |
|
|||||||
|
|
|||||||||
a−1 (j) , j = 2, . . . , n,последовательно переводя |
Рис. 4.5 |
|||||||||
в левую часть уравнения переменные xöj ,приме- |
|
|
||||||||
няя МНК и алгебраически возвращаясь к оценкам исходной формы уравнения.
Дляпредставленияортогональнойрегрессиивобщемслучаеподходятформулы (4.34, 4.36)и другие матричные выраж ения,приведенные выше при описании ортогональной регрессии.Необходимотолько приопределениивекторов иматриц, входящих в эти выражения,заменитьÇ 2ÈнаÇ nÈ.
Спомощьюпреобразованийвпространствепеременныхпередиспользованием ортогональной регрессии и последующего возвращения в исходное пространство
160 |
|
Глава4.Введение в анализ связей |
|
в качестве оценок a−1 |
можно получить любой вектор из множества(симплекса) |
||
|
n |
|
n |
γ1a−1 + |
! |
γj a−1 (j) , γj " 0, j = 1, . . . , n, |
j! |
|
λj = 1. |
||
|
j =2 |
|
=1 |
ЭтоÑподмножествовсехвозможныхМНК-оценокистинныхпараметров α−1.
4.3.Дисперсионный анализ
Дисперсионный анализ заключается в представлении(разложении)дисперсии изучаемых признаков по факторам и использовании F -критерия для сопоставления факторныхÇчастейÈобщей дисперсии с целью определения степени влияния факторов на изучаемые признаки.Примеры использования дисперсионного анализаданы в предыдущемпункте прирассмотрении общейдисперсии моделируемой переменной как суммы объясненной и остаточной дисперсии.
Дисперсионный анализ может бытьодномерным или многомерным.В первом случае имеется только один изучаемый(моделируемый)призна к,во втором случае их несколько.В данном курсе рассматривается только первый случай.Применение методов этого анализа основывается на определенной группировке исходной совокупности(см.п. 1.9).В качестве факторных выступают группирующие признаки.Тоесть изучается влияние группирующих признаков на моделируемый.Если
группирующий(факторный)признак один,то речь идет об |
однофакторном дис- |
персионном анализе,если этих признаков несколькоÑо |
многофакторном ана- |
лизе.Если в группировке для каждого сочетания уровней факторов имеется строго одно наблюдение(численность всех конечных групп в точности равна единице), говорят о дисперсионном анализе без повторений;если конечные группы могут иметь любые численностиÑ с повторениями.Многофакторный дисперсионный анализ может быть полным или частичным.В первом случае исследуется влияние всех возможных сочетаний факторов(смысл этой фразы станет понятным ниже).Во втором случае принимаются во внимание лишь некоторые сочетания факторов.
В этом пункте рассматриваются две модели:однофакторный дисперсионный анализ с повторениями и полный многофакторный анализ без повторений.
Пусть исходная совокупность xi, i = 1, . . . , N сгруппирована по одному фактору,т.е.она разделена на k групп:
xi l Ñзначение изучаемого признака в il -м наблюдении( il = 1, . . . , Nl )
l %
в l-й группе( l = 1, . . . , k); Nl = N .
4.3.Дисперсионный анализ |
161 |
Рассчитываются общая средняя и средние по группам:
|
1 |
|
|
k |
Nl |
1 |
k |
|
xø = |
|
|
|
! !l |
|
!l |
||
|
|
|
|
|
xill = |
|
Nl xøl , |
|
|
N l=1 i =1 |
N |
=1 |
|||||
|
1 |
|
Nl |
|
|
|||
xøl = |
|
|
|
|
i!l |
|
|
|
|
Nl |
|
xill , |
|
|
|||
|
|
|
=1 |
|
|
|||
|
|
|
|
|
|
|
|
|
общая дисперсия,дисперсии по гру ппам и межгрупповая дисперсия( s2q ):
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
k |
Nl |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
!l |
!l |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
s2 = |
N |
|
|
|
(xill − xø)2, |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
=1 i =1 |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
Nl |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i!l |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
sl2 = Nl |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
(xill − xøl )2, |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
k |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
!l |
Nl (øxl − xø)2. |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
sq2 = N |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
=1 |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Общуюдисперсиюможноразложитьнагрупповыеимежгрупповуюдисперсии: |
||||||||||||||||||||||||
|
|
|
1 |
k |
Nl |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
s2 = |
|
|
|
|
((xill − xøl ) + (øxl − xø))2 = |
|
|
|
|
|
|
|
|||||||||||||
|
N |
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
=1 i =1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
!l |
!l |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
k Nl |
|
2 |
|
k Nl |
|
|
|
|
|
1 k Nl |
||||||||||||
= |
|
|
|
|
|
(xill − xøl )2 + |
|
|
|
|
|
|
|
|
|
(xill − xøl) (øxl − xø) + |
|
|
|
(øxl − xø)2 = |
|||||
N |
|
|
|
N |
l=1 i =1 |
N |
|
|
|||||||||||||||||
|
|
|
=1 i =1 |
|
|
|
|
|
|
|
|
|
l=1 i =1 |
||||||||||||
|
|
!l |
!l |
Nl |
|
! !l |
|
|
Nl |
|
|
|
|
! !l |
|||||||||||
|
1 |
|
k |
1 |
|
|
2 |
|
|
k |
|
|
|
|
|
1 |
k |
||||||||
= |
|
|
|
Nl |
|
(xill − xøl )2 + |
|
|
|
|
|
|
(øxl − xø) (xill − xøl ) + |
|
Nl (øxl − xø)2 = |
||||||||||
N |
|
|
Nl |
|
N |
|
l=1 |
N |
|||||||||||||||||
|
|
=1 |
|
|
i =1 |
|
|
|
|
|
|
|
|
i =1 |
|
|
|
|
|
l=1 |
|||||
|
|
!l |
|
|
!l |
|
|
|
|
|
! |
|
|
!l |
|
|
|
|
|
! |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
=0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
←−−−−−−−−→ |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
=0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
←−−−−−−−−−−−−−−−−−−→ |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
Nl sl2 + sq2 = se2 + sq2. |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
N |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
=1 |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
!l |
|
|
|
|
Данноепредставлениеобщейдисперсииизучаемогопризнакааналогичнополученному в начале предыдущего пункта при рассмотрении регрессии,построенной по данным совместного эмпирического распределения признаков.В том случае ÇгруппамиÈвыступали значения первого признака при тех или иных значениях второго признака.В данном случае(в терминах дисперсионного анализа)
s2e Ñвнутригрупповая дисперсия; s2q Ñмежгрупповая дисперсия.
