Линейная регрессия

Предполагается, что между переменными 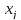, j = 1, . . . , n существует линейная зависимость:

(1.1)

j=1

где α_j , j = 1, . . . , n, β (угловые коэффициенты и свободный член) — параметры (коэффициенты) регрессии (их истинные значения), ε — случайная ошибка; или в векторной форме:

xα = β + ε, (1.2)

где x и α — соответственно вектор-строка переменных и вектор-столбец пара- метров регрессии.

Регрессия называется линейной, если ее уравнение линейно относительно параметров регрессии, а не переменных. Поэтому предполагается, что , j = 1, . . . , n, могут являться результатом каких-либо функциональных преобразований исходных значений переменных.

Для получения оценок 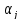, j = 1, . . . , n, b , e, соответственно, параметров регрессии 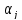, j = 1, . . . , n, β и случайных ошибок ε используется N наблюдений за переменными x, i = 1, . . . , N , которые образуют матрицу наблюдений X размерности N × n (столбцы — переменные, строки — наблюдения). Уравнение регрессии по наблюдениям записывается следующим образом:

Xα = 1_N β + ε, (1.3)

где, как и прежде, 1_N — вектор-столбец размерности N , состоящий из единиц, ε — вектор-столбец размерности N случайных ошибок по наблюдениям; или в оценках:

Xa = 1_N b + e. (6.4)

Собственно уравнение регрессии (без случайных ошибок) xα = β или xa = b определяет, соответственно, истинную или расчетную гиперплоскость (линию, плоскость,...) регрессии.

.

.

Далее применяется метод наименьших квадратов: оценки параметров регрессии находятся так, чтобы минимального значения достигла остаточная дисперсия:

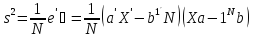
Из равенства нулю производной остаточной дисперсии по свободному члену b

следует, что

x¯a = b (1.5)

и

t

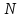e = 0. (1.6)

Действительно,

∂s² 2

−

1

e ₌ r

∂b N ^N





(Xa − 1_N b) =

− 2 (x¯a − b) ,

2

N

^ − _N 1^r e.

Вторая производная по b равна 2, т.е. в найденной точке достигается минимум.

Здесь и ниже используются следующие правила матричной записи результатов диф- ференцирования линейных и квадратичных форм.

Пусть x, a — вектор-столбцы, α — скаляр, а M — симметричная матрица. То- гда:

^dxα = x, ^∂xra = a, ^∂xrM = M, ^∂xrMx = 2M x.

dα ∂x ∂x ∂x

2.2. Простая регрессия

Этот результат означает, что точка средних значений переменных лежит на расчетной гиперплоскости регрессии.

В результате подстановки выражения b из (1.5) через a в (1.4) получается другая форма записи уравнения регрессии:

X^ˆ a = e, (1.7)

где X^ˆ = X − 1_N x¯ — матрица центрированных значений наблюдений.

(1.3, 1.4) — исходная, (1.7) — сокращенная запись уравнения регрессии. Минимизация остаточной дисперсии по a без дополнительных условий приве-

дет к тривиальному результату: a = 0. Чтобы получать нетривиальные решения,

на вектор параметров α и их оценок a необходимо наложить некоторые огра- ничения. В зависимости от формы этих ограничений возникает регрессия разного вида — простая или ортогональная.

1.2. Простая регрессия

В случае, когда ограничения на вектор a (α) имеют вид a_j = 1 ( α_j = 1), возникают простые регрессии. В таких регрессиях в левой части уравнения оста- ется одна переменная (в данном случае j-я), а остальные переменные переносятся в правую часть, и уравнение в исходной форме приобретает вид (регрессия j-й переменной по остальным, j-я регрессия):

X_j = X_−j a_−j + 1_N b_j + e_j , (1.8) где X_j — вектор-столбец наблюдений за j-й переменной — объясняемой,

X_−j — матрица наблюдений размерности N × (n − 1) за остальными перемен- ными — объясняющими (композиция X_j и X_−j образует матрицу X ), a_−j — вектор a без j-го элемента (равного 1), взятый с обратным знаком (компози- ция 1 и −a_−j образует вектор a), b_j и e_j — соответственно свободный член и вектор-столбец остатков в j-й регрессии. В сокращенной форме:

X^ˆ_j = X^ˆ_−j a_−j + e_j . (1.9)

В таких регрессиях ошибки e_ij — расстояния от гиперплоскости регрессии до точек облака наблюдения — измеряются параллельно оси x_j .

Остаточная дисперсия приобретает следующую форму:

_s2 1 1 ^ _ˆ

_ˆ  _{ˆ ˆ} 

_ej = _N e^t e_j = _N

X^t − a^t X^t

^Xj ^{− X}−j ^a−j

. (6.10)

j j −j −j

Из равенства нулю ее производных по параметрам a_−j определяется, что

−j _j −j

a = M ⁻¹m , (1.11)

−

где M_−j =

_ˆ t

1

_N X

−j

_−j — матрица ковариации объясняющих переменных x_−j

_Xˆ

−j _N

между собой, m = ¹ X^{ˆ t}

_Xˆ_j

— вектор-столбец ковариации объясняющих пе-

−j

ременных с объясняемой переменной x_j ; и

cov (X_−j , e_j ) = _N X^ˆ

1

t

−j

e_j = 0. (1.12)

Действительно,

∂s² ₂

^ ˆ ˆ



2

^{ }−2(m_−j − M_−j a_−j ),

ej

∂a_−j

= X^{ˆ r}

−

_N −j

X_j − X_−j

^a−j

=

^ _Xˆ r

_{− N}

_−j e_j .

Кроме того, очевидно, что матрица вторых производных равна 2M_−j , и она, как всякая ковариационная матрица, положительно полуопределена. Следовательно, в найденной точке достигается минимум остаточной дисперсии.

Справедливость утверждения о том, что любая матрица ковариации (теоретическая или ее оценка) положительно полуопределена, а если переменные линейно незави- симы, то — положительно определена, можно доказать в общем случае.

Пусть x — случайный вектор-столбец с нулевым математическим ожиданием. Его

теоретическая матрица ковариации по определению равна E (xx^r). Пусть ξ ƒ= 0 — детерминированный вектор-столбец. Квадратичная форма

(

ξ^rE(xx^r)ξ = E(ξ^rxx^rξ) = E ^ ξ^rx)^2 “ 0,

т.е. матрица положительно полуопределена. Если не существует такого ξ ƒ= 0, что

ξ^rx = 0, т.е. переменные вектора x линейно не зависят друг от друга, то неравенство

выполняется строго, и соответствующая матрица положительно определена.

Пусть X — матрица N наблюдений за переменными x. Оценкой матрицы ко-

вариации этих переменных является

1

¹ X^{ˆ r}X^ˆ . Квадратичная форма

N

¹ ξ^rX^{ˆ r}X^ˆ ξ =

N

= u^ru “ 0, где u = X^ˆ ξ, т.е. матрица положительно полуопределена. Если не

N

существует такого ξ ƒ= 0, что X^ˆ ξ = 0, т.е. переменные x линейно не зависят друг от друга, то неравенство выполняется строго, и соответствующая матрица положи- тельно определена.

Оператор МНК-оценивания образуется соотношениями (6.11) и (6.5), которые в данном случае записываются следующим образом:

b_j = x¯_j − x¯_−j a_−j (6.13)

(соотношения МНК-оценивания (4.37), данные в пункте 4.2 без доказательства, являются частным случаем этого оператора).

Уравнения

m_−j = M_−j a_−j , (6.14)

решение которых дает первую часть оператора МНК-оценивания (6.11), называ- ется системой нормальных уравнений.

МНК-оценки остатков имеют нулевую среднюю (6.6) и не коррелированы (ор- тогональны) с объясняющими переменными уравнения (6.12).

Систему нормальных уравнений можно вывести, используя иную логику. Если

X

j

обе части уравнения регрессии (6.9) умножить слева на ^{ˆ t}

−

1

и разделить на N ,

−j

то получится условие m_−j = M_−j a_−j + _N X^{ˆ t}

e_j , из которого получается искомая

система при требованиях

e¯_j = 0 и cov(X_−j , e_j ) = 0, следующих из полученных

свойств МНК-оценок остатков.

_Zˆ^t_Xˆ

1

1

Такая же логика используется в методе инструментальных переменных. Пусть имеется матрица Z размерности N × (n − 1) наблюдений за некоторыми величи- нами z, называемыми инструментальными переменными, относительно которых известно, что они линейно не зависят от ε_j и коррелированы с переменными X_−j . Умножение обеих частей уравнения регрессии слева на Z^ˆt и деление их на N да-

ет условие

Z^ˆtX^ˆ_j =

N

1

_N −j ^a−j ⁺

Z^ˆte_j , из которого — после отбрасывания

N

второго члена правой части в силу сделанных предположений — следует система

нормальных уравнений метода инструментальных переменных:

_mz

z

z

_−j = M a

, (6.15)

j

где m^z

−

−j

= cov (z, x_j ), M ^z

−j −j

= cov (z, x_−j ).

Значения j-й (объясняемой) переменной, лежащие на гиперплоскости регрес- сии, называются расчетными (по модели регрессии):

_Xc

_j = X_−j a_−j + 1_N b_j , (6.16)

_Xˆ ^c ˆ

_j = X_−j a_−j . (6.17)

Их дисперсия называется объясненной (дисперсия, объясненная регрессией) и может быть представлена в различных вариантах:

_s2 ¹ _{c ˆ c} (6.17)

(6.11) ₁

_qj = _N X^{ˆ t} X

= a^t

^M−j ^a−j

= a^t

m_−j = m^t

a_−j = m^t (6.18)

Если раскрыть скобки в выражении остаточной дисперсии (6.10) и прове-

_s2

сти преобразования в соответствии с (6.11, 6.18), то получается s²

= s² − s² ,

где

_j — дисперсия j-й (объясняемой) переменной, или

ej j qj

_s2 2 2

_j = s_qj + s_ej . (6.19)

Это — дисперсионное тождество, показывающее разложение общей диспер- сии объясняемой переменной на две части — объясненную (регрессией) и оста- точную.

Доля объясненной дисперсии в общей называется коэффициентом детерми- нации:

s

2

_R2

s

=

j ₂

^qj = 1 −

j

_s2

ej

s

₂ , (6.20)

j

который является показателем точности аппроксимации исходных значений объ- ясняемой переменной гиперплоскостью регрессии (объясняющими переменными). Он является квадратом коэффициента множественной корреляции между объ- ясняемой и объясняющими переменными r_j,−j , который, по определению, равен

коэффициенту парной корреляции между исходными и расчетными значениями

объясняемой переменной:

cov ^x_j , x^{c }

_Xˆ t _Xˆ c

X^{ˆ t} X^ˆ a

j

¹ _{j j} (6.17) ¹ _j − j − j

^rj,−j ⁼

^sj ^sqj

= =

N s_j s_qj N

=

^sj ^sqj

s

_m^{t 2}

=

.

_{= −j} ^a−j (6.18)

^sj ^sqj

qj

^sj ^sqj

(6.20)

j

=

R².

Из (6.19) следует, что коэффициент корреляции по абсолютной величине не пре- вышает единицы.

Эти утверждения, начиная с (6.16), обобщают положения, представленные в конце пункта 4.2.

Композиция 1 и −a_j обозначается a(j) и является одной из оценок вектора α. Всего таких оценок имеется n — по числу простых регрессий, в левой части уравнения которых по очереди остаются переменные x_j , j = 1, . . . , n. Эти вектор- столбцы образуют матрицу A. По построению ее диагональные элементы равны единице ( a_jj = 1 вслед за a_j (j) = 1).

Все эти оценки в общем случае различны, т.е. одну из другой нельзя получить алгебраическим преобразованием соответствующих уравнений регрессии:

Это утверждение доказывалось в пункте 4.2 при n = 2. В данном случае спра- ведливо утверждение, что соотношение (6.21) может (при некоторых j, j^t ) вы- полняться как равенство в том и только том случае, если среди переменных x_j , j = 1, . . . , n существуют линейно зависимые.

Достаточность этого утверждения очевидна. Действительно, пусть переменные неко- торого подмножества J линейно зависимы, т.е. существует такой вектор ξ, в кото-

ром ξ_j ƒ= 0 при j ∈ J и ξ_j = 0 при j ∈/ J , и

X^ˆ ξ = 0. Тогда для любого j ∈ J

^ξj

справедливо: a(j) = ¹ ξ, причем a_j^r (j) = 0 при j^r ∈/ J , и e_j = 0, т.е. некоторые

соотношения (6.21) выполняются как равенства.

Для доказательства необходимости утверждения предполагается, что существует такой ξ ƒ= 0, что

Aξ = 0 (6.22)

(т.е., в частности, некоторые соотношения из (6.21) выполняются как равенства).

N

Сначала следует обратить внимание на то, что вслед за (6.14) все компоненты век- тора M a(j) ( M — матрица ковариации всех переменных x: M = ¹ X^{ˆ r}X^ˆ ), кроме

ej

j -й, равны нулю, а j -я компонента этого вектора в силу (6.18, 6.19) равна s² , т.е.

e

MA = S², (6.23)

где S² — диагональная матрица ^.s^{2 .}.

e ej

e

Теперь, после умножения обеих частей полученного матричного соотношения справа на вектор ξ, определенный в (6.22), получается соотношение: 0 = S²ξ, которое

ej

означает, что для всех j , таких, что ξ_j ƒ= 0, s²

= 0, т.е. переменные x_j линейно

зависят друг от друга.

Что и требовалось доказать.

Все возможные геометрические иллюстрации простых регрессий в простран- стве наблюдений и переменных даны в пункте 4.2.