
- •Передмова
- •Розділ І. Лінійна та векторна алгебра
- •§1.1. Матриці, дії над матрицями
- •§1.2. Визначники
- •§1.3. Ранг матриці та способи його обчислення
- •§ 1.4. Обернена матриця
- •§1.5. Системи лінійних рівнянь
- •§1.6. Вектори
- •§1.7. Власні числа та власні вектора
- •§1.8. Квадратичні форми
- •Розділ ІІ. Аналітична геометрія
- •§2.1. Прямокутні координати в просторі. Основні задачі
- •§2.2. Пряма лінія на площині
- •§2.3. Криві лінії другого порядку
- •§ 2.4. Задачі економічного змісту
- •§ 2.5. Площина та пряма в просторі
- •§ 2.6. Нерівності та їх геометричний зміст
- •§ 2.7. Поверхні другого порядку
- •Розділ ІІІ. Вступ до математичного аналізу
- •§4.6. Деякі основні теореми диференційного числення
- •§4.7. Економічний зміст похідної. Еластичність
- •§4.8. Дослідження функцій та побудова їх графіків
- •§5.1. Основні поняття
- •§5.2. Екстремум функції двох змінних
- •§5.3. Метод найменших квадратів
- •Розділ VI. Інтегральне числення
- •§ 6.2. Методи інтегрування
- •§ 6.4. Інтегрування тригонометричних виразів
- •§ 6.5. Інтегрування виразів, що містять ірраціональність
- •§6.8. Геометричні застосування визначенних інтегралів
- •§ 6.10. Наближені обчислення визначеного інтеграла
- •§ 6.11. Невласні інтеграли. Інтеграл ЕйлераAПуассона
- •§ 6.12. Поняття про подвійний інтеграл
- •Розділ VIІ. Диференційні рівняння
- •§ 7.1. Рівняння з відокремленими змінними
- •§ 7.2. Однорідні диференційні рівняння
- •§ 7.3. Лінійне диференціальне рівняння першого порядку
- •Розділ VІІІ. Ряди
- •§ 8.2. Ознаки збіжності рядів з додатними членами
- •§ 8.3. Знакозмінні ряди. Абсолютна та умовна збіжність
- •§ 8.5. Розклад функцій в ряди Тейлора і Маклорена
- •§8.6. Застосування рядів до наближених обчислень
- •§8.7. Ряди Фур’є
- •Відповіді до задач та прикладів
- •Список використаної літератури

Розділ VI. Інтегральне числення
§ 6.11. Невласні інтеграли. Інтеграл ЕйлераAПуассона
6.11.1. Поняття і різновиди власних інтегралів
Згідно з теоремою існування визначеного інтеграла цей інтеграл існує, якщо виконані умови:
1)відрізок інтегрування [a; b] скінчений;
2)підінтегральна функція f(x) неперервна або обмежена і має скінчену кількість точок розриву.
Якщо хоч би одна із цих умов не виконується, то визначений
інтеграл називають невласним. Якщо не виконується перша умова, тобто b = / ; або а = / ; або а = / і b = / , то інтеграли назива+ ють невласними інтегралами з нескінченими межами. Якщо не вико+ нується лише друга умова, то підінтегральна функція f(x) має точки
розриву на відрізку [a; b]. В цьому випадку Hb |
f (x)dx називають не |
a |
|
власним інтегралом від розривної функції, необмеженої в точках відрізку інтегрування.
6.11.2. Дослідження невласних інтегралів
Дослідження невласних інтегралів проводять шляхом викорис+ тання граничного переходу у визначеному інтегралі.
Інтеграли з необмеженими межами визначають так:
/H a
/
H
/
f (x)dx = limb9/ Hb |
f (x)dx ; |
Hb |
f (x)dx = |
alim9 / Hb |
f (x)dx ; |
|
|
|
a |
|
/ |
|
a |
|
|
f (x)dx = Hc |
f (x)dx + /H f (x)dx = alim9 / Hc |
f (x)dx + limb9/ Hb |
f (x)dx . |
||||
/ |
|
c |
|
a |
|
c |
|
Якщо вказані границі існують (будуть скінченими числами), то відповідний інтеграл називають збіжним, і він дорівнює своїй гра+ ниці. Якщо якась границя не існує або дорівнює нескінченності, то інтеграл називають розбіжним.
453

Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»
/ dx
Приклад 6.289. Обчислити інтеграл H1 x2 1 або встановити його
розбіжність.
Розв’язок. Згідно з означенням невласного інтеграла маємо:
/ dx |
= lim b |
dx |
|
|
|
||||||||
= lim arctg x |
b |
= lim (arctg b – arctg 1) = |
|||||||||||
|
|
|
|
|
|||||||||
H1 x2 1 |
|
b9/ H1 x2 1 |
b9/ |
1 |
b9/ |
|
|
|
|||||
|
|
|
|
|
|
|
|||||||
= $ – |
$ |
= $ . |
|
|
|
|
|
|
|
||||
2 |
|
4 |
4 |
|
|
|
|
|
|
|
|||
Отже, цей інтеграл існує, збіжний і дорівнює $ . |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
Приклад 6.290. Встановити збіжність або розбіжність |
/H |
dx |
. |
||||||||||
p |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
1 |
x |
||
|
|
|
|
|
|
|
|
|
|
|
|
||
Розв’язок. Згідно з означенням невласного інтеграла маємо:
/ dx |
= lim b |
dx |
|
= lim |
|
x p 1 |
|
b |
= – |
1 |
|
( lim |
1 |
– 1) = |
||||||||||||
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
H1 x p |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
b9/ H1 x p |
|
b9/ |
|
p 1 |
|
1 |
|
|
p |
1 b9/ |
bp 1 |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
1 |
|
, |
p . 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
= p |
1 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
/, |
p , 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Отже, при р > 1 інтеграл збіжний, а при p < 1 — розбіжний. |
||||||||||||||||||||||||||
Розглянемо випадок р = 1. |
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
/ dx |
= lim b |
|
dx |
|
|
|
|||||||||||||||||
|
|
|
|
= lim ln|x| |
b = lim ln b + ln 1 = / . |
|||||||||||||||||||||
|
|
|
H |
|
x |
|
|
|||||||||||||||||||
|
|
|
b9/ H x |
b9/ |
1 |
|
b9/ |
|
|
|
|
|||||||||||||||
|
|
|
1 |
|
|
|
1 |
|
|
|
|
|
|
|
|
/ |
dx |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Таким чином, при р = 1 інтеграл H |
|
— розбіжний. |
||||||||||||||||||||||||
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
x |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Одержали, що інтеграл |
/H |
dx |
збіжний при p>1, і розбіжний при p 1. |
p |
|||
|
1 |
x |
|
|
|
|
|
454
Розділ VI. Інтегральне числення
Приклад 6.291. Обчислити |
/H ex dx |
або встановити його роз+ |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
/ |
|
|
|
|
|
|
|
біжність. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Розв’язок. Дослідимо на збіжність інтеграли H0 |
ex dx |
і |
/Hex dx . |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
/ |
|
|
0 |
|
|
|
|
|
|
|
0 |
|
|
|
0 |
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
H |
ex dx |
= lim |
ex dx = lim |
ех |
= lim (е0 – еа) = 1, |
||||||||||
|
|
|
|
|
|
|
|
|
a9 / H |
|
|
|
a9 / |
|
a |
a9 / |
|
|
|
||
|
|
|
|
|
|
/ |
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
тобто, перший інтеграл збігається до 1. |
|
|
|
|
|||||||||||||||||
Але |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
/ |
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
H |
ex dx = lim |
H |
ex dx = lim |
(еb – 1) = / , |
|
|
|||||||
|
|
|
|
|
|
|
|
|
b9/ |
|
|
b9/ |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
0 |
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
/ |
|
|
|
|
|
|
|
|
|
|
|
/ |
|
|
|
|||||
тобто Hex dx |
є розбіжним. Отже, і інтеграл H ex dx є розбіжним. |
||||||||||||||||||||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
/ |
|
|
|
|||||
В курсі теорії ймовірностей зустрічається невласний інтеграл |
|||||||||||||||||||||
/ |
|
|
x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
H e |
|
|
dx , що називається інтегралом Ейлера Пуассона. Доведено, що |
||||||||||||||||||
2 |
|||||||||||||||||||||
/ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
/ |
x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
H e |
|
|
|
= |
|
2$ , іншими словами площа S під кривою Гаусса |
|||||||||||||||
|
|
2 |
dx |
|
|||||||||||||||||
/ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
e |
x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
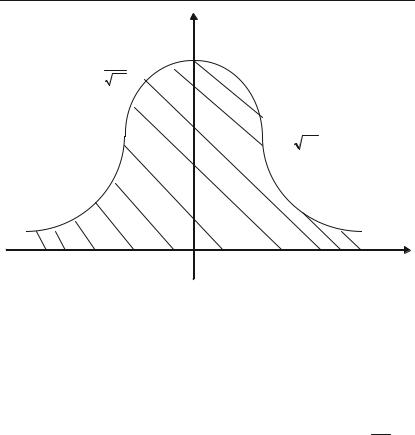
y |
2 |
на інтервалі ( / ; / ) дорівнює 1 (див. рис. 6.14). |
|||||||||||||||||||
2$ |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
У випадку необмеженої на [a; b] функції f(x) її точки розриву можуть бути на лівому кінці або на правому кінці, або в середині проміжку інтегрування [a; b]. У цих випадках невласні інтеграли визначаються так:
Hb |
f (x)dx = limе90 |
bHе f (x)dx ; |
Hb |
f (x)dx = limе90 |
Hb |
f (x)dx ; |
a |
|
a |
а |
|
a е |
|
455
Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»
Y
1
2$
|
1 |
e |
x2 |
|
y |
2 |
|||
|
||||
2$ |
|
|
||
S = 1
|
|
|
|
0 |
|
|
X |
|
|
|
|
Рис.6.14. |
|
|
|
и |
|
|
c е' |
|
b |
|
|
H |
f (x)dx |
= lim |
H |
f (x)dx |
+ lim |
H |
f (x)dx . |
|
е'90 |
|
е''90 |
|
|||
а |
|
|
a |
|
|
c е'' |
|
Якщо вказані границі існують, то відповідний інтеграл назива+ ють збіжним. У протилежному випадку інтеграл називають розбіж ним.
1 dx
Приклад 6.292. Встановити збіжність, або розбіжність H0 x p .
Розв’язок. Функція необмежена при x = 0. Згідно з означенням невласного інтеграла маємо:
1 dx |
= lim |
1 |
|
dx |
= lim |
x p 1 |
|
1 |
= |
1 |
|
( lim |
1 |
|
|
) = |
|||||
|
|
|
|
1 |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
H x p |
|
е90 |
H |
|
x p |
е90 |
p 1 |
0 |
е |
|
p 1 |
е90 |
х p 1 |
|
0 е |
|
|||||
0 |
|
1 |
|
|
0 е |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
, |
p |
,1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
= |
p 1 |
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
/, p &1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
456
Розділ VI. Інтегральне числення
6.11.3. Приклади для самостійного розв’язку
6.294. Обчислити невласні інтеграли (або встановити їх розбіж+ ність):
|
/ dx |
|
|
|
|
1/ 2 |
|
|
|
dx |
|
|
|
|
|
||||||||
а) |
H |
|
|
|
|
; |
|
б) |
H |
|
|
|
|
|
|
|
; |
|
|||||
|
x |
3 |
|
x ln |
2 |
|
|
||||||||||||||||
|
1 |
|
|
|
|
|
|
0 |
|
|
x |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
в) |
/He 2x dx ; |
г) H1 |
|
dx |
; |
|
|
|
|
|
|
|
|||||||||||
3 |
|
|
|
|
|
|
|
|
|||||||||||||||
|
0 |
|
|
|
|
|
|
|
0 |
|
|
|
|
x |
|
|
|
|
|
|
|
||
д) |
H3 |
|
|
dx |
; |
ж) |
/H |
|
|
|
|
dx |
|
|
; |
||||||||
|
|
2 |
|
|
2 |
|
|
|
|
|
|||||||||||||
|
0 |
|
(x 1) |
|
/ x |
|
|
2x 2 |
|||||||||||||||
з) |
H1 ln xdx ; |
и) |
H3 |
|
|
xdx |
|
; |
|
|
|||||||||||||
3 |
2 |
|
|
||||||||||||||||||||
|
0 |
|
|
|
|
|
|
|
2 |
|
|
|
x |
4 |
|
|
|
|
|||||
|
0 |
|
|
|
|
|
|
|
6 |
|
|
|
|
|
dx |
|
|
|
|
|
|||
і) |
H xex dx ; |
ї) |
H |
|
|
|
|
|
|
|
|
. |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
3 (5 x) |
2 |
|
||||||||||||||||||||
|
/ |
|
|
|
|
|
2 |
|
|
|
|
|
|||||||||||
457
