Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»

§ 2.6. Нерівності та їх геометричний зміст

Метод координат дозволяє геометрично тлумачити не тільки рівняння, а також і нерівності.

Подібно тому, як ми говоримо, що рівняння з двома змінними х та у F(x, y) = 0 визначає на площині деяку лінію, можна сказати, що нерівність з двома змінними х та у F(x, y) < 0 визначає множину точок площини, координати яких задовольняють цій нерівності. Та+ ким чином геометрично тлумачать і нерівність F(x, y) > 0.

Якщо вираз F(x, y) є лінійним, тобто F(x, y) = Ах + Ву + С, де А, В, С – сталі, то ми маємо лінійне рівняння

Якщо коефіцієнти А і В не дорівнюють одночасно нулю, то рівнян+ ня (2.40) визначає на площині пряму, а нерівності (2.41) і (2.42) — відповідно дві півплощини, на які пряма (2.40) розбиває всю коор+ динатну площину. Для того щоб з’ясувати, яка із цих двох півпло+ щин визначається заданою лінійною нерівністю, можна застосувати, наприклад, такий спосіб.

Виберемо яку+небудь точку, підставляємо її координати в нерівність, що перевіряється.

Якщо координати точки задовольняють нерівність, то нерівність визначає ту площину, в якій знаходиться вибрана точка; якщо ж координати точки не задовольняють нерівність, то нерівність визна+ чає площину, яка не містить вибраної точки.

Приклад. Записати з допомогою нерівності ту півплощину, в якій лежить точка М(4; 5) та границею якої є пряма 3х – 2у + 5 = 0. Перевірити, лежить в цій же півплощині початок координат.

Розв’язок. Підставимо координати точки М в ліву частину рівнян+ ня заданої прямої: 3 4 – 2 5 + 5 = 7. Одержана величина додатна. Отже, точка М не лежить на заданій прямій, а шукана площина виз+ начається нерівністю 3х – 2у + 5 > 0.

Студенту рекомендовано зробити малюнок і розв’язати самостійно другу частину приклада.

148

Розділ II. Аналітична геометрія

Можна розглянути також систему нерівності:

F1(x, y) , 0

,F2 (x, y) 0

... ... ... ...

Fm (x, y) , 0

Областю розв’язання системи нерівностей називається множина всіх точок, координати кожної із них задовольняють всім нерівнос+ тям системи.

Перерізом кількох множин точок називається множина точок, кожна із яких належить всім множинам, що перетинаються. Очевид+ но, областю розв’язання системи нерівностей служить переріз обла+ стей розв’язання кожної із нерівностей системи.

Областю розв’язків, системи лінійних нерівностей

є, очевидно переріз півплощин, що визначаються кожною із нерівно+ стей системи. Ця область може бути і пустою множиною, тобто мно+ жиною, яка не містить ні одної точки (півплощини не мають спільних точок).

Якщо ж ця множина точок не пуста, то вона називається много+ кутною областю. Якщо, крім того, ця область обмежена, тобто на містить точок з як завгодно великим значенням координат, то її на+ зивають многокутником.

Приклад. Записати з допомогою системи нерівностей множину точок, що лежать всередині трикутника з вершинами А(2; 1), В(6; 3), С(4; 5).

Розв’язок. Студенту рекомендовано зробити Рис.. Очевидно, мно+ жину всіх внутрішніх точок трикутника АВС можна розглянути як перетин трьох півплощин, з яких перша обмежена прямою АВ і містить

149

Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»

точку С, друга обмежена прямою ВС і містить точку А, третя обме+ жена прямою АС і містить точку В.

Знайдемо нерівність, що визначає першу із цих півплощин. Скла+ демо рівняння прямої АВ, знаючи координати точок А і В:

Підставляючи в ліву частину цього рівняння координати точки С, одержуємо 4 – 25 = –6 < 0. Отже, перша півплощина визначаєть+ ся нерівністю

х – 2у < 0.

Аналогічно, площина, що обмежена прямою ВС і містить точку А, визначається нерівністю:

х+ у – 9 < 0.

Аплощина, що обмежена прямою АС і містить точку В — не+ рівністю:

2х – у – 3 < 0.

Отже множина всіх внутрішніх точок трикутника АВС визна+ чається системою нерівностей

2x y 3 , 0.

Якщо замість строгих нерівностей (< або >) розглядати не строгі

нерівності ( або & ), то в визначеній ними області включаються і границі цих півплощин.

Наприклад область розв’язків нерівностей:

є область, що обмежена трикутником АВС, включаючи як її внутрішні, так і граничні точки, тобто і точки відрізків АВ, ВС, АС.

150

Розділ II. Аналітична геометрія

Аналогічно інтерпретуються геометрично лінійні нерівності з трьома змінними. Лінійна нерівність з трьома невідомими визначає півпростір, а система таких нерівностей – переріз півпростору. Якщо він не порожній, є многогранною областю або, в випадку обмеже+ ності, многогранником.

2.6.1. Приклади розв’язання задач.

Задача 2.121. Побудувати область розв’язків системи лінійних нерівностей:

2x1 5x2 & 10;

x

1 3;

3x1 3x2 12;

x1 2x2 & 12.

Розв’язок. Будуємо граничні прямі, що відповідають даним не+ рівностям, за двома точками, що відповідають цим прямим:

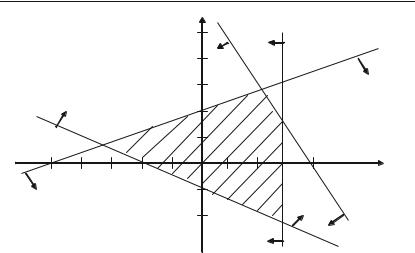
Кожна пряма ділить площину на дві півплощини. Та з них, що містить початок координат, і є областю розв’язків кожної з нерівно+ стей (координати точки О(0; 0) задовольняють кожній нерівності). Стрілками позначимо півплощини, які є областями розв’язків даних нерівностей. Перетин відмічених півплощин — чотирикутник АВСD — є область розв’язків даної системи (рис. 2.21).

Задача 2.122. Побудувати область розв’язків системи лінійних нерівностей:

151

Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»

Розв’язок. Будуємо граничні прямі, що відповідають даним не+ рівностям:

(l1): –х1 + х1 = 6, A1(0; 6) l1, A2(–6; 0) l1;

(l2): 3х1 + 5х2 = 15, B1(0; 3) l2, B2(5; 0) l2; (l3): x2 = 1.

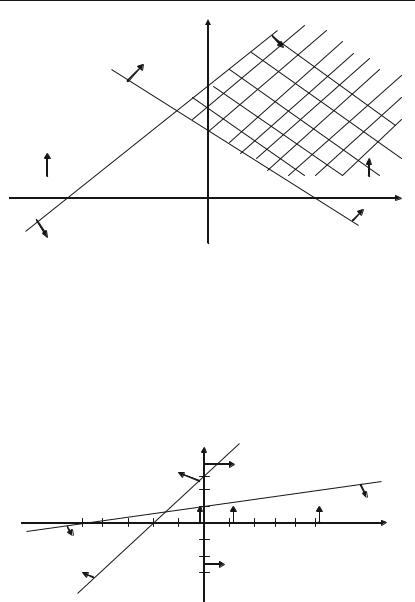
Область розв’язків першої прямої містить початок координат, а область розв’язків другої і третьої нерівностей — не містять початку координат (координати точки О(0; 0) не задовольняють другій і третій нерівностям). Стрілками позначимо півплощини, точки яких задо+ вольняють нерівностям. Областю розв’язків є опукла необмежена область (рис. 2.22).

Задача 2.123. Побудувати область розв’язків системи лінійних нерівностей:

152

Розділ II. Аналітична геометрія

Х2

Будуємо область розв’язків кожної нерівності (рис. 2.23).

Не існує жодної точки, загальної для всіх площин, що відповіда+ ють даним рівнянням. Отже, область розв’язків порожня. Система нерівностей несумісна.

Рис. 2.23.

153

Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»

2.6.2. Задачі для самостійного розв’язку

2.124. Побудувати області, координати яких задовольняють не+ рівностям:

а) у < 2 – x, x > –2, y > –2. б) y > 2 – x, x < 4, y < 0.

в) 4x 2y 1, y & x + 2, x & –4.

2.125. Побудувати область розв’язків системи лінійних нерівно+

154