Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Черноморский государственный университет им. Петра Могилы

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Вища математика.pdf

Скачиваний:

124

Добавлен:

23.03.2015

Размер:

3.55 Mб

Скачать

☆

<<< < Предыдущая 14 15 16 17 18 19 20 21 22 23 24 2526 / 4026 27 28 29 30 31 32 33 34 35 36 37 38 > Следующая >>>

Розділ VI. Інтегральне числення

§ 6.5. Інтегрування виразів, що містять ірраціональність

m r

6.5.1. Інтеграли вигляду HR(x, x n ,..., x 5 )dx

m r

Розглянемо інтеграл HR(x, x n ,..., x 5 )dx , де R — раціональна

функція своїх аргументів. Інтеграл такого вигляду знаходиться за до+ помогою підстановки:

x = tk; dx = ktk – 1dt,

(6.19)

де k — спільний знаменник дробів mn , ..., rs .

6.5.1.1. Розв’язання прикладів


Приклад 6.153. Знайти інтеграл H				x			dx .
Приклад 6.153. Знайти інтеграл H	3		2		4		dx .
		x				x
Розв’язок. Спільний знаменних дробових показників								1	,	2	,	1
						2				3		4

змінної х дорівнює 12. Виконаємо підстановку x = t12, dx = 12t11dt, t = 12 x . Одержимо:

= H

t12

12t

= H

12t11dt

12 2

4 x

)

= 12 H

t17dt

= 12 H

t14dt

t3 (t5 1)

t5 1

Одержали неправильний дріб. Необхідно виділити цілу частину.

407

Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»

t14

|t5 – 1

t14 – t9

|t9 + t4 + t4/(t5 – 1)

t9 – t4

12 H

t dt

= 12 H(t9 t4

)dt

= 12 Ht9dt + 12 Ht4dt +

+ 12

t10

dt =

+ 12

ln|t5 – 1| + C =

(12 x )10 +

H t5 1

(12 x )5 +

5 +

12 x5

ln|(12 x )5

– 1| + C =

ln|12

x5 – 1| + C.

6.5.2. Інтеграли вигляду

R x,

ax b

,...,

ax b s

cx d

b n

ax b s

Інтеграли вигляду

dx , де

,...,

cx d

приводяться до раціональної функції за допомогою підста+

новки

ax b

= tk, де k — спільний знаменник дробів

, ...,

cx d

408

Розділ VI. Інтегральне числення

6.5.2.1. Розв’язання прикладів

Приклад 6.154. Знайти інтеграл H	1		1 x		dx.

	x	2		x

Розв’язок. Виконаємо підстановки t2 = 1 x x , звідки

12tdt

x = t2 1 , dx = (t2 1)2 .

1 x

dx = H

2tdt

= –2 Ht

dt = –2

+ C =

(t2 1)2

1 x 3

= C –

6.5.3. Інтеграли, що потребують тригонометричної підстановки

До інтегралів від функцій, що раціонально залежать від тригоно+ метричних функцій, приводяться інтеграли:

HR(x,	a2 x2 )dx — підстановкою x = a sin t;		(6.20)
HR(x,	a2	x2 )dx — підстановкою x = a tg t;	(6.21)
HR(x,	x2	a2 )dx — підстановкою x = a/cos t.	(6.22)

6.5.3.1. Розв’язання прикладів

Знайти інтеграли.

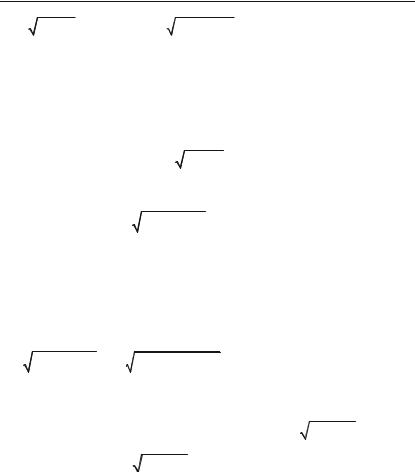
Приклад 6.155. H x2 4 x2 dx .

Розв’язок. Застосовуємо підстановку x = a sin t, одержуємо

dx = 2cos tdt, і якщо sin t = x2 , то t = arcsin x2 .

409

Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»

Hx2

4 x2 dx = H(2sint)2 4 4sin2 t 2costdt = H4sin2 t 4cos2 tdt =

= 4 Hsin

2tdt = 4 H

1 cos 4t

= 2 Hdt – 2 Hcos4tdt

= 2t –

sin4t + C = 2arcsin

–

sin4(arcsin

) + C =

= 2arcsin

4 x

(x2 – 2)

+ C.

Приклад 6.156. H

(36 x

2 3

)

Розв’язок. Застосовуємо підстановку x = 6tg t, одержуємо

dx =

dt, і якщо x = 6tg t, то t = arctg

cos2 t

= H

cos2 t

Hcostdt =

(36 x2 )3

(36 36tg2 t)3

cos3 t

sin t + C =

sin(arctg

) + C =

+ C.

36 x2

Приклад 6.157. H

x2 25dx

Розв’язок. Застосовуємо підстановку x

, одержуємо

cos t

5sin tdt

якщо x

, cos t =

, t = arccos

cos2 t

cos t

410

Розділ VI. Інтегральне числення

									5	2									sin t
										25							5	2			sin tdt
										25								2
H			x2	25dx		= H	cost					5sin t							cost
															dt =		H		cost							=
				x	4				5	4		cos	2	t	dt =		H	4	1					2		=
				x					5			cos		t			5	4	1			cos		2	t
																			cos	4	t
																				4
								cost
=		1		Hsin2 t costdt			=		1		sin3 t	+ C =				1	sin3(arccos					5	) + C =
	25								25	3						75						x
=			1		(x2 25)3		+ C.
=	75				x3		+ C.

6.5.4. Приклади для самостійного розв’язку

Знайти інтеграли:

6.158.

dx .

6.160.

dx .

6.162. H

(4 x 3 1) x 3

6.164. H

1 x2

dx .

6.166. H

x2dx

25 x

6.168. H

x2dx

(4 x2 ) 4 x2

6.170. H

16 x2 dx .

6.159.

dx .

H x(

x 3

x )

6.161. H

1 4 x

dx .

6.163.

x 1

dx .

6.165. H

x2 9

6.167. H

x 3

x 8

6.169. H

(9 x2 )

9 x2

6.171. H

x2 36

dx .

411

Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»

§ 6.6. Визначений інтеграл. Властивості визначеного інтеграла. Формула НьютонаAЛейбтіца

Якщо функція f(x) неперервна на відрізку [a; b] (де а < b), і якщо: 1) розбити цей відрізок довільним чином на n частинних відрізків

довжиною x1 , x2 , ..., xn ;

2) вибрати на кожному частинному відрізку по одній довільній точці -1 , -2 , ..., -n ;

3)обчислити значення функції f(x) у вибраних точках;

4)скласти суму

	n
f(-1 ) x1 + f(-	2 ) x2 + ... + f(-n ) xn = f (-i ) xi ,
	i 1

то вона називається інтегральною сумою f(x) на відрізку [a; b]. Якщо по різному ділити відрізок [a; b] на n частинних відрізків і

по+різному вибирати на них по одній точці -i , то можна для будь+

якої неперервної заданої функції f(x) і будь+якого заданого відрізка [a; b] скласти нескінчену множину різних інтегральних сум. При цьому виявляється, що всі ці різні інтегральні суми при необмеже+ ному зростанні n при прямуванні до нуля найбільшої із довжин ча+ стинного відрізка, мають одну і ту ж границю. Ця границя всіх інтег+ ральних сум функції f(x) на відрізку [a; b] називається визначеним

інтегралом від f(x) в межах від а до b та позначається Hb f (x)dx .

6.6.1. Найпростіші властивості визначеного інтеграла

1. При перестановці меж інтегрування знак інтегралу змінюється на протилежний:

Hb	f (x)dx = – Ha	f (x)dx .	(6.23)
a	b

412

Розділ VI. Інтегральне числення

2. Інтеграл з однаковими межами дорівнює нулю:

Ha f (x)dx = 0.

3. Відрізок інтегрування можна розбити на частини:

Hb	f (x)dx = Hc	f (x)dx + Hb	f (x)dx .	(6.24)
a	a	c

4. Інтеграл від алгебраїчної суми функцій дорівнює сумі інтег+ ралів від кожного доданку:

Hb	(f1(x) f2 (x) f3 (x))dx = Hb	f1(x)dx + Hb	f2 (x)dx – Hb	f3 (x)dx . (6.25)
a	a	a	a

5. Постійний множник k можна виносити за знак інтеграла:

Hb kf (x)dx = k Hb		f (x)dx .	(6.26)
a	a

6. Якщо функція y = f(x) неперервна на відрізку [a; b] (де a < b), то знайдеться таке значення I [a; b], що виконується рівність:

Hb	f (x)dx = f(I )(b – a) (теорема про середнє).	(6.27)
a

Для обчислення визначеного інтеграла, коли можна знайти відповідний невизначений інтеграл, служить формула Ньютона+ Лейбніца:

b		b
H f (x)dx	= F(x)	b	= F(b) – F(a),	(6.28)
H f (x)dx	= F(x)	a	= F(b) – F(a),	(6.28)
a

— визначений інтеграл дорівнює різниці значень невизначеного інтег+ рала при верхній та нижній межах інтегрування.

413

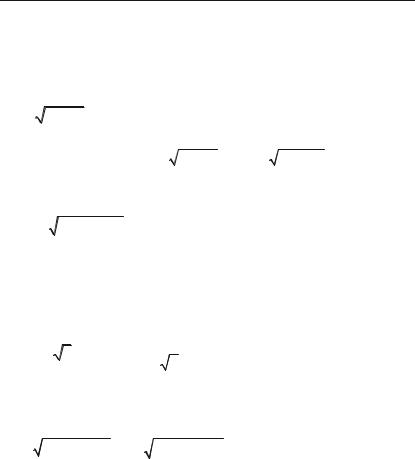
Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»

6.6.2. Розв’язання прикладів

Обчислити інтеграли.

Приклад 6.172.

7			dx				7				1/ 2					1		7				1/ 2
H					=		H(3x 4)						dx =					H(3x				4)	3dx =
H		3x 4			=		H(3x 4)						dx =			3		H(3x				4)	3dx =
1		3x 4					1									3		1
					1/ 2 1			7			2								2
					1/ 2 1			7
=		1 (3x 4)							=			3x 4				7		=			3 7 4 –
		3	1								3					1
								1											3
								1											3
				2	1
–		2	3 ( 1)			4 =				2	5 –			2	1 =		8	= 2		2	.
	3								3				3			3				3

Приклад 6.173.

H2 sin				x	dx		= 2 H2 sin				x		1		dx	= –2cos				x	$2	= –2cos			$		+ 2cos	0	=
H2 sin					dx		= 2 H2 sin								dx	= –2cos						= –2cos					+ 2cos		=
0			2					0	2 2								2				0				4			2
= –2			2				+ 2	1 = 2 – 2 .
= –2			2				+ 2	1 = 2 – 2 .
			2
Приклад 6.174.
5				dx					5						dx								x 2			5
5									5
H									= H										= arcsin								=

			4x x					2									2						3			2
2	5								2				9 (x				2)						3			2
2	5								2				9 (x				2)
= arcsin						5 2		– arcsin						2 2			= arcsin 1 – arcsin 0 =										$ .
							3					3															2
Приклад 6.175.
0				dx					0				dx											0
0									0
H1									H1
								=										= arctg(x				+ 1)		1 =
		x2 2x 2						=		(x 1)2 1								= arctg(x				+ 1)		1 =
		x2 2x 2								(x 1)2 1
= arctg 1 – arctg 0 =												$ .
												4

414

Розділ VI. Інтегральне числення

Приклад 6.176.

16			dx						16						(	x 9				x )dx
H			dx					=		H					(	x 9				x )dx				=
H		x 9 x						=		H		(		x 9 x )( x 9								x )		=
0		x 9 x								0		(		x 9 x )( x 9								x )
	16 (		x 9					x)dx						1	16							1		16		1/ 2
= H													=		H( x 9 x)dx =									H(x		9)	dx +
= H			x 9 x										=	9	H( x 9 x)dx =							9		H(x		9)	dx +
	0		x 9 x											9	0							9		0
	1		16	1/ 2					1		(x 9)3 / 2						16		1 x3 / 2		16			2			3	16
	1		16	1/ 2					1		(x 9)3 / 2						16		1 x3 / 2		16			2			3	16
+			H x			dx	=										+					=			(x 9)			+
	9		0						9				3/ 2				0	9		3/ 2	0	27						0
	2								2														2
+	2		x3		16		=		2	(			(16 9)3 –					(0 9)3 ) +					2	( 163		–	03 ) =
+	27		x3		0		=	27		(			(16 9)3 –					(0 9)3 ) +				27		( 163		–	03 ) =
	27				0			27														27

= 272 (125 – 27) + 272 64 = 272 162 = 12.

Приклад 6.177.

;

x(1 x

)

x x

Mx N

A Ax2 Mx2 Nx

;

x(1 x2 )

1 x2

x(1 x2 )

A + Ax2 + Mx2 + Nx = 1;

A M 0

M 1,

N 0

N 0,

A 1

A 1.

–

;

x(1 x2 )

1 x2

2 dx

xdx

= H1

–

= ln|x|

1 –

ln|1+ x2|

= ln2 – ln1 –

x(1 x2 )

1 x2

415

Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»

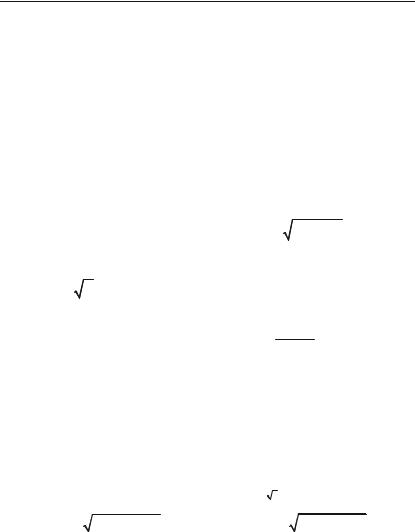
–	1	ln5 +	1	ln2 =	3	ln2 –	1	ln5 =	1	(ln8 – ln5)	=	1	ln	8	.
							2
	2		2		2				2			2		5

6.6.3. Приклади для самостійного розв’язання

Обчислити інтеграли.

6.178. H3				(2x3 x2 5)dx .
	2
	1							dx
6.180. H								dx						.

													3
	2			(11 5x)
6.182. H9					y 1						dy .
6.182. H9											dy .
	4					y 1
	3				xdx
6.184. H										.
6.184. H				x		2	1			.
	2			x			1
	2
	2			x 3
6.186. H										dx .
6.186. H			x2 4							dx .
	0
6.188. $Hsin								x	cos			x			dx .
6.188. $Hsin									cos						dx .
	0						2						2
	0
		1								dx
6.190.	H									dx							.

							8 2x x									2
	0,5						8 2x x
	$
6.192.	H2							dx					.
6.192.	H2												.
		$ 1 cos x
		2
		2

6.179. H2 (x3 4x)dx .

2
13			dx
6.181. H			dx			.

		5	(3 x)	4
2		5	(3 x)
1			dx
6.183. H			dx		.

	x	2
0	x		4x 5
0

4 dx

6.185. H$ cos2 x .

2						dx
6.187. H						dx						.

			x	2
1			x		5x 4
1
6.189. $Hcos						x			cos		3x		dx .
6.189. $Hcos						2			cos		2		dx .
0						2					2
0
	3 1								dx
6.191.		H							dx						.

						3 2x x								2
		0				3 2x x
	2	sin				1		dx
	$					1
	$
6.193. H						x
										.
					x		2			.
	1				x
$

416

Розділ VI. Інтегральне числення

$
4	sin x
6.194. H				dx .
6.194. H	cos	2	x	dx .
0	cos		x
0
$
6.196. H2	cos x cos3 xdx .
$

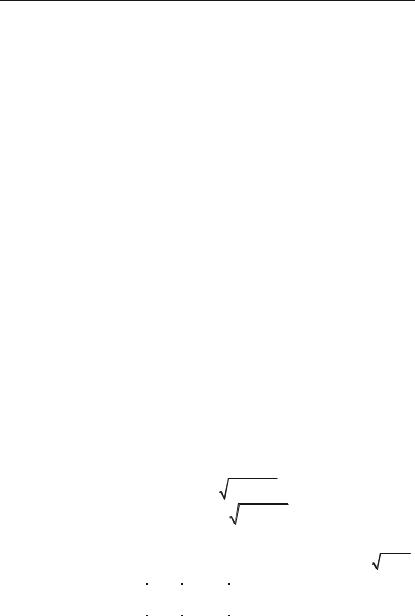
6.195. H2 sin2 2xdx .

3 dx

6.197. H2 2x2 3x 2 .

417

Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»

§6.7. Методи підстановки та інтегрування частинами

увизначеному інтегралі

Для обчислення багатьох визначених інтегралів необхідно замі+ няти змінну інтегрування. При цьому, якщо визначений інтеграл

Hb	f (x)dx перетворюється за допомогою підстановки x = (t) в
a

інший інтеграл, з новою змінною t, то задані межі x1 = a i x2 = b заміняються новими межами t1 = ; i t2 = ? , які визначаються із

вибраної підстановки, тобто із рівнянь a = (;) , b = (? ) . Якщо

'	f ( (t)) неперервні та відрізку [; ; ? ], то
(t) і	f ( (t)) неперервні та відрізку [; ; ? ], то
	b	?
	H f (x)dx = H f ( (t)) '(t)dt .		(6.29)
	a	;

Якщо підінтегральний вираз у визначеному інтегралі можна пред+ ставити в вигляді добутку двох співмножників u та dv, то для обчис+ лення визначеного інтегралу необхідно скористатися формулою інтег+ рування частинами у визначеному інтегралі:

Hb udv = uv			ab – Hb vdu .		(6.30)
a			a

6.7.1. Розв’язання прикладів
29		3 (x 2)2
Приклад 6.198. Обчислити H				dx .
		2
3	3	3 (x 2)

Розв’язок. Введемо підстановку x – 2 = t3, x = t3 + 2, dx = 3t2dt.

Знайдемо нові межі інтегрування, використовуючи рівняння t = 3 x 2 :

x	3	29
t	1	3

418

Розділ VI. Інтегральне числення

Одержуємо

29 3 (x 2)2														3		t2 3t2dt							3 t4dt									3		t4 9 9
H3										dx = H1										= 3 H1										= 3 H1								dt =
H3	3 3 (x 2)2									dx = H1						3 t2				= 3 H1					3 t2					= 3 H1						3 t2		dt =
3				4	9							9				3																			3
= 3 H			t		9							9			dt = 3 H(t2							3						9		)dt = 3 Ht2dt –
					2				2																			9
					2		t		2																		t	2
1		3 t					t							3		1											t	3							1
3						3								9							t3								3			27
3						3								9							t3		3						3			27					t		3
– 9 Hdt					+ 27 H												dt =	3								– 9t				+						arctg			=
											2					2					3		1						1
											2					2
1						1		t					( 3)																				3				3		1
= 27 – 1 – 27 + 9 + 9																3 (аrctg			3				– arctg							1	) =
= 27 – 1 – 27 + 9 + 9																3 (аrctg					3		– arctg							3	) =
																					3									3
= 8 + 9 3						$							$					3			$					16 3 3$
														= 8 + 9							6	=											.
													6	= 8 + 9								=						2					.
						3							6															2
Приклад 6.199. Обчислити H4																				xdx				.
Приклад 6.199. Обчислити H4																								.
																	1 1					x
Розв’язок. Введемо підстановку x = t2, dx = 2tdt,																																			x = t.
Знайдемо нові межи інтегрування використовуючи рівність t =																																							x .
Спочатку в рівність t =															x підставимо нижню межу інтегрування х = 1,

а потім верхню х = 4, і одержуємо: при х = 1 t = 1; при x = 4t = 2. Нові межі інтегрування 1 t 2. Переходимо до обчислення:

4		xdx					2	t2tdt			2	t2dt		2		t2 1			1
H					= H					= 2 H				= 2 H						dt =
	1 x								1 t			1 t				1 t
1							1				1			1
		2	t2 1						1			2				1			2		2
= 2 H										dt	= 2 H t			1			dt		= 2 Htdt		– 2 Hdt +
					1				t 1
		1	t									1			t 1				1		1
		2		1						t2			2					2
											2
+ 2		H1				dt			= 2		– 2t			+ 2ln\|t+1\|					= 4 – 1 – 4 + 2 +

			t	1						2	1		1					1

419

Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»

+ 2ln 3 – 2ln 2 = 1 + 2(ln 3 – ln 2) = 1 + 2ln 32 = 1 + ln 49 .

														$
Приклад 6.200. Обчислити H2																				dx				.
Приклад 6.200. Обчислити H2																								.
														0		2 cos x
Розв’язок. Замінюючи змінну за допомогою підстановки tg																															x	= t,
Розв’язок. Замінюючи змінну за допомогою підстановки tg																																= t,
																												2
знайдемо cos x =				1 t2				, dx			=		2dt						, та нові межі інтегрування t													= 0
знайдемо cos x =								, dx			=								, та нові межі інтегрування t													= 0
				1 t2								1		t			2											1
при x	= 0, та t = 1 при х										= $ .
1			2							2		2
												2
$				1			2dt								1
2	dx			1		1 t				2					1					dt					2			t		1
H	dx				H							= 2 H								dt					2			t		1
			=																				=				arctg			=

	cos x							1	t		2							t	2		3				3			3
0 2	cos x			0		2		1	t						0			t			3				3			3		0
						2		1	t		2
								1	t		2
=	2	(arctg		1		– arctg						0		) =						2		(	$		– 0) =			$	.
	3			3								3								3			6				3	3
															3			(x3 1)dx
Приклад 6.201. Обчислити														H												.
Приклад 6.201. Обчислити														H				x		2	4 x				2	.
														1				x			4 x

Розв’язок. Введемо підстановку x = 2sin t. Одержуємо dx = 2cos tdt, та нові межі інтегрування:

x		1	3
t = arcsin	x	$	$
		6	3
2

420

Розділ VI. Інтегральне числення

							$														$
3	(x3 1)dx						3	((2sint)3 1)2costdt													3	(8sin3 t 1)dt
H						=	H													= H									=
H	x	2	4 x		2	=	H					2						2		= H				4sin		2	t		=
1	x		4 x				$ (2sint)								4 (2sint)						$			4sin			t
							6														6
	$					1	$										$						$
	$						$										$						$
	3						3			dt									1
	3						3			dt							3		1				3
= 2 Hsin tdt					+		H							= –2cos t			$	–			ctg t		$ =
= 2 Hsin tdt					+	4	H		sin		2	t		= –2cos t			$	–	4		ctg t		$ =
	$						$
	$						$										6						6
	6						6										6						6
	6						6
= –2(cos $					– cos $ ) –								1	(ctg $		– ctg		$ ) = –2(						1	–		3	) –
= –2(cos $					– cos $ ) –							4		(ctg $		– ctg		$ ) = –2(						1	–		3	) –
			3				6					4			3			6					2				2
–	1	(	3	–		3 ) =					7			– 1.
–	4	(	3	–		3 ) =				2		3		– 1.
	4		3							2		3

Приклад 6.202. Обчислити H (x 3)sin5xdx .

Розв’язок. Для обчислення даного інтеграла використаємо фор+

				b			b				b
мулу інтегрування частинами: Hudv					= uv		b	– Hvdu .
мулу інтегрування частинами: Hudv					= uv		a	– Hvdu .
				a							a
				a							a
		u (x 3),	dv sin5xdx					1
		u (x 3),	dv sin5xdx
		du dx,	v Hsin5xdx						cos5x
		du dx,	v Hsin5xdx					5	cos5x
	$					$					$
	$										$
10			1					1		10
10			1			2		1		10
	H (x 3)sin5xdx = –			(x + 3)cos5x			+				H (x 3)sin 5xdx =
	H (x 3)sin5xdx = –		5	(x + 3)cos5x		0	+	5			H (x 3)sin 5xdx =
0										0
0										0

	1		$	$		1		(0 + 3)cos 5 0 +	1
= –		(		+ 3)cos 5		+				sin 5x
	5		10		10		5		25

2 =

421

Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»

=	1	( $ 30 )cos			$		+		3		cos 0 +							1		sin 5			$		–		1		sin 5		0 =
	5	10			2		5											25					10			25
=	1	( $ 30 )0 +				3	1 +						1				1 –		1		0 =			3	+	1		=		16	= 0,64.
	5	10			5							25						25					5			25				25
Приклад 6.203. Обчислити H1 arcsin xdx .
															0
Розв’язок.
				u arcsin x,															dv dx
				u arcsin x,															dv dx
				du								1					dx,		v x

												x2
							1					x2
H1 arcsin xdx = xarcsin x										1			–			H1	xdx				= 1 arcsin 1 –
										1							xdx
										0							2
0										0						0	1 x
0															$	0	1 x
– 0 arcsin 0 + 1 x
							2	1									– 1.
								0 =							2		– 1.
															2
Приклад 6.204. Обчислити H1																x arctg xdx .
															0
Розв’язок.
			u arcctg x,													dv xdx						x2
			u arcctg x,													dv xdx
			du				dx							,		v H xdx
			du				1 x					2		,		v H xdx
							1 x														2

Застосовуючи до заданого інтеграла формулу інтегрування час+ тинами, одержимо:

H1	x arctg xdx =	x2	arctg x		–	1	x2		dx		=	1	$ –	1	1	x2 1	1	dx =
				1
				0		H0				2					H0	2
0	2						2	1	x			2 4		2		1 x

422

Розділ VI. Інтегральне числення

	$		1	( H1 dx – H1				dx			) = $ –									1									$			1
=	$	–	1					dx												1	(x		10 – arctg x					10 ) =	$	–		1	(1 – 0 –
=		–						2													(x		10 – arctg x					10 ) =		–			(1 – 0 –
	8	2		0	0	1 x					8					2													8			2
	8	2				1 x					8					2													8			2

– arctg 1 + arctg 0) =								$ –				1	(1 –			$ ) =						$ –			1	+	$	= $	–		1	=		$ 2	.
								8			2					4						8			2		8	4		2			4
	Приклад 6.205. Обчислити He ln2 xdx .
																1
	Розв’язок. Нехай
									u ln2 x,								1						dv dx
									u ln2 x,														dv dx
									du 2ln x										dx, v x
									du 2ln x										dx, v x
																	x
	He ln2 xdx = xln2x						1e – He 2ln x										1	xdx = eln2e – 1ln21 – 2 He ln xdx =
																	1

	1										1						x													1
	1										1																			1
	= e – 2 He ln xdx =
				1
										u ln x,											dv dx
										u ln x,											dv dx
										du				1	dx,						v x
										du					dx,						v x
														x
	= e – 2 He ln xdx = e – 2(xln x																1e – He						1	xdx ) = e – 2(eln e – 1ln 1 –
																							1

				1																	1		x
				1																	1

– x 1e ) = e – 2e + 2e – 2 = e – 2.

Пригадаємо, що ln 1 = 0, ln e = 1.

423

Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»

6.7.2. Приклади для самостійного розв’язку

6.206. H5		xdx		.
6.206. H5				.
0		1 3x
4		dx
6.208. H		dx			.

	1		2x 1
0	1		2x 1
6.210. lnH5		ex	ex 1			dx .
6.210. lnH5			x			dx .
0		e	3
0

6.212. H11 3 x 1 .

6.207. H9	xdx	.

4	x 1
6.209. H5	xdx		.

1	4x 5

H2 dx

6.211. 0 1 sin x cos x .

6.213. Ha	x cos	x	dx .

a		a

$

6.214.

6.216.

6.218.

6.220.

6.222.

H2 ln xdx .

1 x5

H2 x ln(x 1)dx .

H1 x2 e –2xdx.

3	dx
	dx	.

H1 x2 1 x2
H1 x2 1 x2

H1 x ln(1 x2 )dx .

6.215. H4 x tg2 xdx .

6.217. He ln2 xdx .

1 x2

6.219. H2 (x2 1)sin 2xdx .

0
2	4 x2
6.221. H			dx .
6.221. H	x	2	dx .
1	x
1

424

<<< < Предыдущая 14 15 16 17 18 19 20 21 22 23 24 2526 / 4026 27 28 29 30 31 32 33 34 35 36 37 38 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
23.03.2015161.79 Кб12В начале было слово или след на воде.doc
#
23.03.2015201.73 Кб12ВАРІАНТИ_для_Excel 105-106.doc
#
23.03.2015481.28 Кб33ВДЛ.Переклад.doc
#
08.03.201689.83 Кб19ВДЛ.Філологія-2015.docx
#
23.03.2015274.59 Кб13вентиляція.docx
#
23.03.20153.55 Mб124Вища математика.pdf
#
23.03.201536.86 Кб9Вопросы к экзамену по вышмат.doc
#
23.03.2015123.39 Кб42Вплив на людину джерел - реферат.doc
#
23.03.2015305.66 Кб12ВСДС_Білети.doc
#
23.03.201584.61 Кб3ВСТУП 3.docx
#
23.03.201593.04 Кб5ВСТУП 5.docx