1. Средняя арифметическая простая

2.Средняя арифметическая взвешенная

В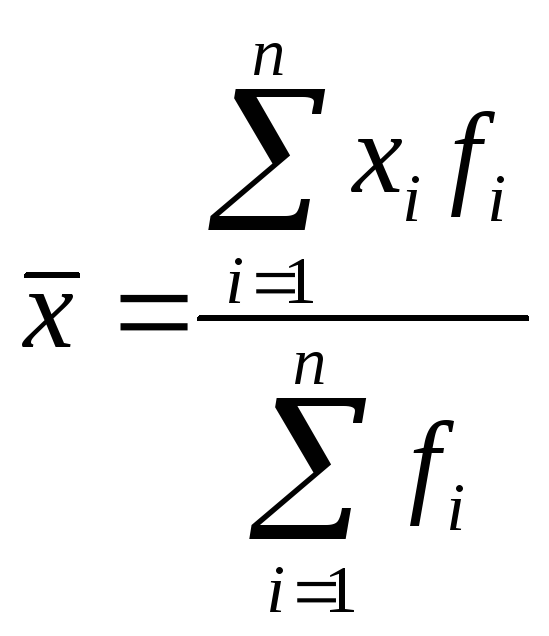практических исследованиях отдельные значения изучаемого признака встречаются несколько раз у единиц исследуемой совокупности. В этом случае частота повторения индивидуальных значений признака (вес) присутствует в расчетной формуле.

Следовательно, для исчисления взвешенной средней выполняются следующие последовательные операции:

• умножение каждого варианта на его частоту;

• суммирование полученных произведений;

• деление полученной частоты на сумму частот.

В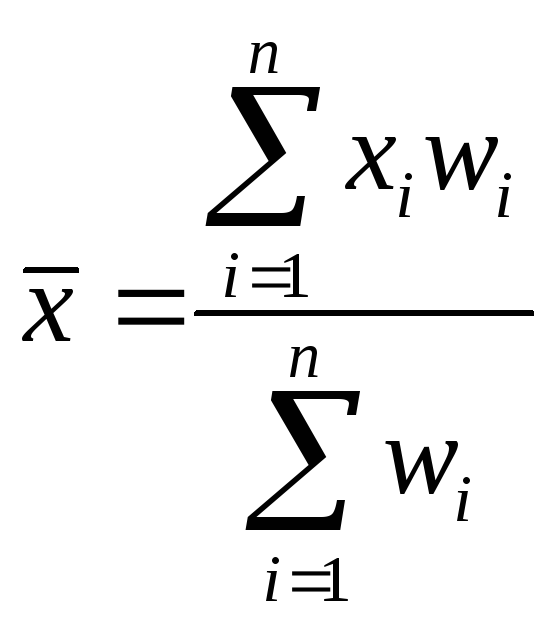ряде случаев роль частот при исчислении средней играют частости (относительная величина структуры), средняя будет определяться так:

Часто вычисление средних величин приходится производить по данным,

сгруппированным в виде интервальных рядов.

Для вычисления средней величины надо в каждом варианте определить серединное значение , после чего произвести взвешивание обычным порядком.

В закрытом интервале серединное значение определяется как полусумма значений

нижней и верхней границы.

Воткрытом интервале предполагается, что расстояние между границами данного

интервала такое же, как в соседнем интервале.

Например: Определить среднюю заработную плату рабочих, если имеются следующие данные (Табл. 7.).

Таблица 7.

Заработная плата рабочих (руб.)	Число человек
до 5000	5
5000-7000	7
7000-9000	8
9000-11000	11
свыше 11000	9

Так как группы представлены в виде интервалов, то для определения средней необходимо определить, прежде всего, серединное значение интервалов.

Первый интервал – открытый.

Согласно правилу он будет заменен на интервал от 3000 до 5000.

2. Определим среднюю заработную плату по формуле средней арифметической взвешенной.

В) Средняя гармоническая

Средняя гармоническая – это величина, обратная средней арифметической. Она применяется, когда статистическая информация не содержит частот по определенным вариантам совокупности, а представлена как их произведение.

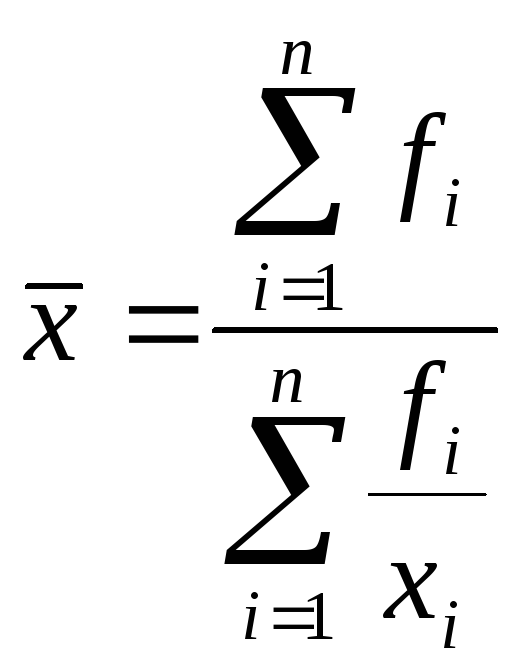- средняя гармоническая взвешенная (можно определить частоту или вес).

-средняя гармоническая взвешенная (можно определить частость)

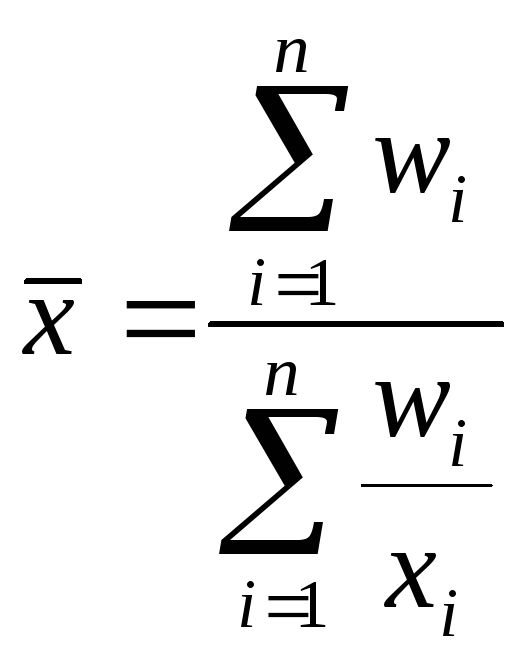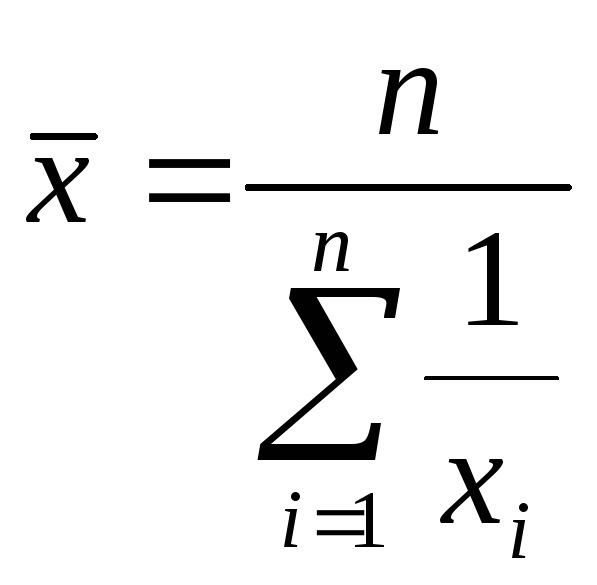- средняя гармоническая простая

Если веса у каждого значения признака равны, то можно использовать среднюю гармоническую простую.

Однако в статистической практике чаще применяется средняя гармоническая взвешенная.

Как видно, средняя гармоническая является превращенной формой арифметической

средней. Вместо гармонической всегда можно вычислить арифметическую среднюю, но для этого надо сначала определить веса отдельных значений признака.

Напр.: Определить среднюю цену изделия на основании имеющихся данных (Табл. 8.):

Вид изделия	Цена одного изделия (тыс.руб.)	Стоимость всех изделий (тыс.руб.)
А	4	80
Б	8	240
В	10	600

Р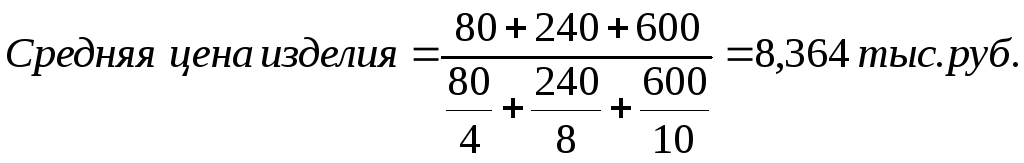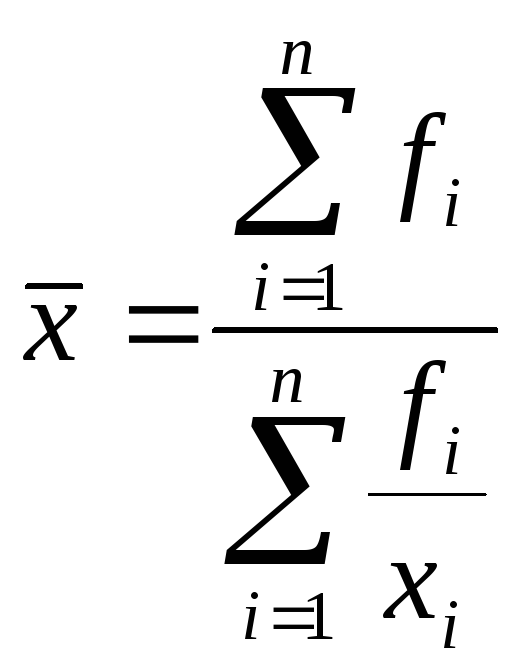ешение: Воспользуемся средней гармонической взвешенной.

Г) Мода и медиана

Мода и медиана применяются для характеристики структуры совокупности, поэтому и называются структурными средними, в отличие от других средних (арифметической, гармонической), которые называются степенными.

Модой (М_о) называется чаще всего встречающееся значение признака у единиц данной совокупности.

Мода широко используется в коммерческой практике при изучении покупательского спроса (при определении размеров одежды, обуви, которые пользуются широким спросом). Например, по приведенным ниже данным, наибольшим спросом пользуется 37 размер обуви.

Таблица 9

Размер обуви	34	35	36	37	38	39	40
Число покупателей	2	10	20	88	19	9	1

В интервальном ряду модой приближенно считают центральный вариант так называемого модального интервала, т.е. того интервала, который имеет наибольшую частоту (частость). В пределах интервала надо найти то значение, которое является модой.

Конкретное значение моды для интервального ряда определяется по формуле:

- нижняя граница модального интервала;

- величина модального интервала;

- частота, модального интервала;

- частота интервала, предшествующего модальному;

- частота интервала, следующего за модальным.

Например: Таблица 10.

Стаж (лет), Xi	До 2	2-4	4-6	6-8	8-10	Св. 10
Число работников, fi	4	23	20	35	11	7
Накопленная частота, Si	4	27	47	82	93	100

При этом =5,94 года.

Эта формула основана на предположении, что расстояние от нижней границы модального интервала до моды и от моды до верхней границы модального интервала прямо пропорционально разностям между численностью модального интервала и прилегающих к нему.

Медиана () – это величина, которая делит численность упорядоченного вариационного ряда на две равные части: одна часть имеет значения варьирующего признака меньше, чем средний вариант, а другая – большие.