
OFP-Tretyak-Lozovski
.pdf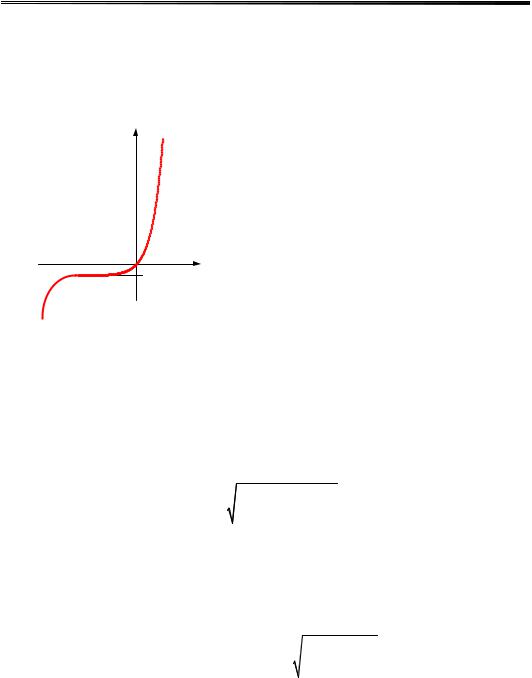
ОСНОВИ ФІЗИКИ НАПІВПРОВІДНИКІВ |
68 |
визначається концентрацією носіїв, то згідно із (14.117) та (14.118), можна записати
|
|
j = js (eeV /kT −1), |
(14.119) |
|
де js – струм насичення. |
|
Якісний вигляд вольт-амперної |
||
j |
|
|||
|
характеристики |
p-n-переходу |
||
|
|
подано на рис.14.17. Для детальні- |
||
|
|
шого аналізу цієї характеристики |
||
|
|
припустимо що утворюється ко- |
||
|
|
нтакт між двома напівпровідни- |
||
|
|
ками різного типу провідності p- |
||
0 |
|
та n-. Для спрощення припустимо, |
||
|
що межа розподілу між ними є |
|||
jS |
φ |
|||
різкою, тобто при x > 0 – розта- |
||||
|
|
шована область напівпровідника |
||
|
|
n-типу, а при x < 0 – напівпрові- |
||
Рис.14.17 |
|
дника p-типу. У системі встано- |
||
Вольт-амперна характеристика |
вився рівень Фермі, однаковий |
|||
p-n-переходу |
|
для обох її частин. Хід потенціалу |
||
|
|
|||
в області межі розподілу та його залежність від координати в наближенні сталої концентрації носіїв заряду в ОПЗ знайдено раніше ((14.104) і (14.105)). Залежність довжини L від зовнішньої різниці потенціалів можна знайти, оскільки зовнішня різниця потенціалів, як і у випадку бар'єру Шотткі або зменшує, або збільшує висоту бар'єру на межі по-
ділу. Використовуючи (14.117) для випадку pp >> nn , |
знайдемо |
|||
|
|
|
|
|
L = |
ε |
(ϕC ±V ). |
(14.120) |
|
|
||||
|
2πenn |
|
||
Ясно, що змінюючи прикладену зовнішню напругу, ми змінюємо величину області просторового заряду, яка утворює плоский конденсатор. Таким чином, зміна V спричиняє зміну заряду цього конденсатора Q. Величина C = dQ /dV – ємністю, зумовлена просторовим (фіксованим)
зарядом на іонізованих домішках. Вона називається бар'єрною, і за аналогією з ємністю плоского конденсатора її можна записати як
|
|
|
|
C = S |
εenn |
. |
(14.121) |
|
|||
b |
8π(ϕC +V ) |
|
|
|
|
||
На ефекті зміни ємності за зміни зовнішньої різниці потенціалів будуються прилади, що називаються варикапами або варакторами.
Розглянемо динаміку носіїв заряду у p-n-переході. Для цього припустимо, що легування обох частин напівпровідника відбувалось так,



71 |
Розділ 14. КОНТАКТНІ ЯВИЩА У НАПІВПРОВІДНИКАХ |
може призводити до багатьох неприємностей – від різкого зменшення рухливості носіїв до відшарування плівок від підкладок – тобто до неможливості утворення гетероструктури як такої.
Згідно із табл. 14.1 систему AlGaAs/GaAs можна розглядати як приклад, де сталі ґратки збігаються. Дійсно, ця система має незначний незбіг сталих ґратки (~ 0,1 %) у широкому діапазоні співвідношень концентрацій від Al до Ga. Такі структури виростають вільними від механічних напружень і надзвичайно досконалими – вони є основою для виготовлення промислово значимих гетероструктур. Іншим прикладом широко використовуваної системи для конструювання гетероструктур є GaAs/Ga1–xInxAs і Ga1–xAlxAs/Ga1-xInxAs. Такі структури використовуються, наприклад для виготовлення польових транзисто-
рів (field-effect transistor).
|
|
|
|
Таблиця 14.1 |
|
|
|
|
|
|
|
|
|
|
Коефіцієнт |
Енергія |
|
|
Eg (eВ) |
|
лінійного |
||
|
Стала ґратки |
електронної |
|||
Напівпровідник |
розширення |
||||
при T = 300 K |
(нм) |
спорідненості |
|||
при T = 300 K |
|||||
|
|
|
(eВ) |
||
|
|
|
(10–4 K–1) |
||
|
|
|
|
||
Ge |
0,67 |
0,5658 |
5.7 |
4.13 |
|
Si |
1,11 |
0.5431 |
2.33 |
4.01 |
|
GaAs |
1,43 |
0.5653 |
5.8 |
4.07 |
|
AlAs |
2,15 |
0.5661 |
5.2 |
|
|
GaP |
2,25 |
0.5451 |
5.3 |
4.3 |
|
GaSb |
0,68 |
0.6095 |
6.9 |
5.06 |
|
AlSb |
1,6 |
0.6136 |
3.7 |
3.65 |
Тепер, коли ми розібрались з деякими технологічними проблемами, що виникають при утворенні гетерограниць, спробуємо з'ясувати, яким чином формуватимуться енергетичні бар'єри у таких структурах. Для цього уявимо, що ми створюємо гетеропереход із двох напівпровідників, які характеризуються забороненими зонами E g1 та Eg2.
Нехай для визначеності Eg2 > E g1. Яку енергетичну діаграму матиме утворений гетероперехід (рис. 14.18) а), б) чи в)?

ОСНОВИ ФІЗИКИ НАПІВПРОВІДНИКІВ |
72 |
|
|
|
|
Eg 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
Eg1 |
|
|
|
|
||
Eg1 |
|
|
|
|
Eg1 |
|
|
|
|
Eg 2 |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
Eg 2 |
|||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
(a) |
|
|
|
|
|
(б) |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
(в) |
|||||||||||
|
|
|
|
|
|
|
|
Рис. 14.18 |
|
|
|
|
|
|||||
|
|
|
|
|
|
Можливі типи гетеропереходів |
|
|
|
|
|
|||||||
Зрозуміло, що три можливі гетеропереходи мають принципово різний вигляд енергетикних діаграм, отже й різні електронні властивості. Який все ж таки тип енергетичної структури можна отримати, з'єднавши два напівпровідника із визначеними значеннями зонної щілини? Або що ми отримаємо у результаті такого "зонного конструювання" (до речі, в англомовній літературі цей процес так і називається band engineering). Відповідь на питання про формування гетеробар'єру надає так зване правило Андерсона, що базується на фундаментальному енергетичному параметрі – електронній спорідненості матеріалів χ – енергії, яка необхідна для видалення електрона із дна зони провідності EC на вакуумний рівень (тобто видалення електрона із кристала). Ідея Андерсона базується на очевидному припущенні, що абсолютне значення вакуумного рівня є однаковим для всіх матеріалів. Звідси
маємо, що різниця між енергіями дна зони провідності в гетеропере- |
||||||||||||||||||||||||||
ході |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
вакуумний рівень |
|
|
|
|
|
|
∆E |
|
= E(2) − E(1) = χ − χ |
. |
(14.133) |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
χ2 |
|
|
|
|
|
|
|
|
C |
C |
C |
|
1 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
χ1 |
|
|
|
|
|
|
|
|
|
|
|
|
Тоді, якщо відоме значення різ- |
||||||||||||
|
|
|
|
EC(2) |
|
|
|
|
|
|
|
|
|
ниці |
|
енергій забороненої |
зони |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
EC(1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
∆EC |
∆Eg , то легко визначається різ- |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ниця між рівнями стель валентної |
||||||||||||
|
Eg1 |
|
|
|
|
Eg 2 |
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
EV(1) |
|
|
|
|
|
|
|
|
|
|
зони (рис. 14.19) |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
∆E |
|
|
∆EV |
= ∆Eg − ∆EC . |
(14.134) |
||||||||
|
|
|
(2) |
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
EV |
|
|
|
|
|
|
V |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Наприклад, розглянемо гетеросис- |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
Рис. 14.19 |
|
|
|
|
|
|
тему GaAs-Al0.3Ga0.7As. Відомо, що |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
χGaAs = 4,07, |
а χAl |
0.3 |
Ga |
0.7 |
As = 3,74eB. |
||||||||
|
Побудова енергетичної діаграми |
Звідси ∆EC |
|
|
|
|
|
|||||||||||||||||||
гетеро переходу за правилом Андерсена |
= 0,33eB. Оскільки |
|||||||||||||||||||||||||

73 |
Розділ 14. КОНТАКТНІ ЯВИЩА У НАПІВПРОВІДНИКАХ |
різниця енергії |
зонних щілин ∆Eg = 0,37eB, то отримуємо |
∆EV = 0,04eB.
Таким чином утворюється гетеропереход, де зонна щілина матеріалу, який має менше значення ширини забороненої зони, розташований усередині енергетичного зазору зонної щілини матеріалу, що має більшу величину забороненої зони. Такий гетероперехід називається гетеропереходом І типу (рис. 14.20 а).
Іншим прикладом гетероперехода є так званий гетеропереход ІІ типу (рис. 14.20 б). Існує й третя можливість поєднання двох напівпро-
|
GaAs |
Al0.3Ga0.7As |
|
InP |
|
In0.52Al0.48As |
|
|
|
|
GaSb |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
1.8 eV |
|
|
|
|
|
1.44 eV |
|
InAs |
|
0.73 eV |
|||||
1.43 eV |
|
|
|
|
|
|
|
||||||||||||
|
|
1.35 eV |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
0.36 eV |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
б |
|
|
|
в |
|||||||
Рис. 14.20
Гетеропереходи І (a), II (б), та ІІІ (в) типів
відникових материалів у гетероструктуру – це так звана гетероструктура ІІІ типу. У цьому випадку на межі розподілу відбувається перекриття забороненої зони одного із компонентів гетеросистеми. Англійською мовою цей тип гетеросистеми так і називається – broken-gap aligment. Класичним прикладом гетеросистеми ІІІ типу є гетеропереход InAs-GaSb. Цей приклад як енергетичну діаграму подано на рис. 14.20 в. Завдяки тому, що тут перекриваються зона провідності одного компонента із валентною зоною іншого, електрони та дірки спонтанно переходитимуть з одного боку на інший, доки не будуть зупинені наведеним електричним полем, аналогічно тому, як формується область збіднення у p-n діоді. Залежно від наявності домішок обидва напівпровідники, що утворюють гетероперехід, можуть мати:
однаковий тип провідності – тоді іноді їх називають ізотипними гетеропереходами,
різний тип провідності – про такі переходи говорять як про анізотипні.
Зрозуміло, що енергетичні діаграми гетеропереходів, що містять вигини зон і виникаючі при цьому потенціальні бар'єри, відрізняються від діаграм для гомопереходів. Для демонстрації цього розглянемо побудову зонної діаграми ідеального різкого n-p-гетеропереходу,

ОСНОВИ ФІЗИКИ НАПІВПРОВІДНИКІВ |
74 |
вважаючи, що більшою величиною забороненої зони характеризується напівпровідник p-типу. Припустимо, що напівпровідник n-типу розташований в області x < 0, а напівпровідник p-типу – в області x > 0.
Гетерограниця збігається із площиною x = 0. При приведенні напівпровідників (рис. 14.19) у контакт у системі встановиться термодинамічна рівновага, що характеризується єдинім Фермі-рівнем для обох
напівпровідників і |
наявністю контактної різниці потенціалів |
ϕC = (Φ1 − Φ2 )/e, де Φ1 |
і Φ2 – роботи виходу напівпровідників n- та |
p-типів, відповідно. В ідеальному різкому гетеропереході контактний потенціал V (x) та енергія електрона поблизу поверхні зразка eϕ(x)
мають бути неперервними функціями координати x, нормальної до гетерограниці. При цьому виконується рівність eϕ(x) =V (x). Це приводить
до того, що нормальна компонента вектора електричної індукції також має бути неперервною: D1 = D2. Якщо напівпровідники характеризу-
ються діелектричної сприйнятливостями ε1 та ε2, то маємо
ε1E1 = ε2E2, |
(14.135) |
де E1 та E2 – нормальні компоненти електричного поля в |
n- та |
p-напівпровідниках поблизу межі розподілу. Тому на границі гетеропереходу нормальна компонента електричного поля має розрив. А оскільки
E(x) = − dV (x) |
, |
(14.136) |
dx |
|
|
то величини V (x) і ϕ(x) мають злам. Якщо припустити, що електронна
спорідненість та енергія забороненої зони напівпровідників, що утворюють гетероперехід, є сталими вздовж зразків аж до межі ро з- поділу та не дорівнюють одне одному, то на границі гетеропереходу відбуваються стрибки згідно із правилом Андерсена (див. (14.133) і (14.134) ∆EC = χ1 − χ2, ∆EV = Eg2 − Eg1 − ∆EC . Знайдемо хід країв зон E C (x) та
EV (x) по обидва боки гетероперходу із умови неперервності нормаль-
ної компоненти електричної індукції на межі розподілу (14.135), яку із врахуванням (14.136) можна записати у вигляді
dϕ1 |
|
|
|
dϕ2 |
|
|
|
|
|
|
|
|
|||
ε1 dx |
|
x =−0 |
= ε2 |
dx |
|
x =+0 . |
(14.137) |
|
|
|
|
При цьому вважатимемо, що повна контактні різниця потенціалів ϕC
розподіляється між двома напівпровідниками на частини ϕC |
та ϕC |
2 |
|
|
1 |
|
|
так, що |
|
|
|
ϕC = ϕC |
+ ϕC . |
(14.138) |
|
1 |
2 |
|
|

75 |
Розділ 14. КОНТАКТНІ ЯВИЩА У НАПІВПРОВІДНИКАХ |
Припустимо, що напівпровідники леговані мілкими домішками так, що донори та акцептори є повністю іонізованими, а концентрацією електронів і дірок у глибині зразків n- та p-типів є n0 та p0 , відповідно.
Тоді рівняння Пуассона по обидва боки переходу можна записати у вигляді
|
|
|
|
|
|
|
d2ϕ |
= − |
4πen |
0 |
, |
|
x < 0, |
|
|
|
|
|
|
|
(14.139) |
||||||||||||||||
|
|
|
|
|
|
|
dx2 |
|
ε |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
d2ϕ |
= |
4πep |
0 , |
|
x > 0. |
|
|
|
|
|
|
|
(14.140) |
|||||||||||||||||
|
|
|
|
|
|
|
dx2 |
|
|
ε2 |
|
|
|
|
|
|
|
|
|||||||||||||||||||
Інтегруючи ці рівняння із граничними умовами |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
ϕ |
|
|
= ϕ , |
|
dϕ |
|
|
|
= 0; ϕ |
|
|
|
|
|
|
= ϕ |
, |
|
dϕ |
|
|
= 0, (14.141) |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
x =−d1 1 |
|
dx |
x =−d |
|
|
|
|
|
|
|
|
|
|
|
|
x =d2 |
2 |
|
|
dx |
|
x =d |
2 |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
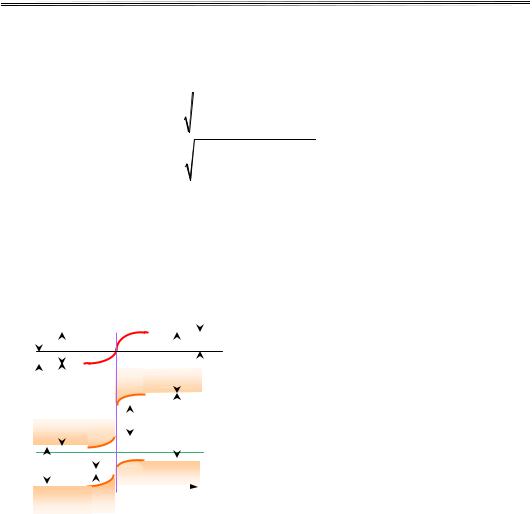
отримуємо хід потенціалу |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
2πen0 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
в n-області |
|
|
|
|
|
ϕ (x) |
= ϕ − |
(x −d )2 |
, |
|
|
|
(14.142) |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
1 |
|
|
|
1 |
|
|
|
|
|
|
ε1 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
p-області |
|
|
|
|
|
ϕ (x) = ϕ |
+ |
2πen0 |
(x + d |
2 |
)2. |
|
|
|
(14.143) |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
2 |
|
|
|
|
2 |
|
|
|
|
|
|
|
ε2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Підставляючи ці розв'язки до (14.137), отримаємо |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
d1 = |
|
|
p0 |
. |
|
|
|
|
|
|
|
|
|
|
(14.144) |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
d2 |
|
n0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Покладемо |
у |
формулах |
(14.143) |
|
та |
|
|
(14.144) x = 0. |
Зауважуючи, що |
||||||||||||||||||||||||||||
ϕ1(0)− ϕ1 = ϕC |
|
і |
|
ϕ2 − ϕ2(0) = ϕC |
|
, |
знайдемо |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
1 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ϕ |
|
= |
2πen0 |
d2 |
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
(14.145) |
|||||||||||
|
|
|
|
|
|
|
C |
|
|
|
|
ε1 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
ϕ |
|
= 2πep0 |
d2. |
|
|
|
|
|
|
|
|
|
|
|
|
|
(14.146) |
|||||||||||||
|
|
|
|
|
|
|
C2 |
|
|
|
ε2 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Повна контактна різниця потенціалів звідси |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
ϕC |
|
= 2πe |
n0d1 |
|
|
|
+ |
p0d2 |
. |
|
|
|
|
(14.147) |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ε1 |
|
|
|
|
|
|
|
ε2 |
|
|
|
|
|
|
|
||||||||
Використовуючи співвідношення (14.144), із (14.145-146) отримуємо |
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
ϕC |
|
|
|
p |
0 |
|
ε |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
= |
|
|
|
|
|
2 . |
|
|
|
|
|
|
|
|
(14.148) |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
ϕ |
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
ε |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
C2 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
||||||||
77 |
Розділ 14. КОНТАКТНІ ЯВИЩА У НАПІВПРОВІДНИКАХ |
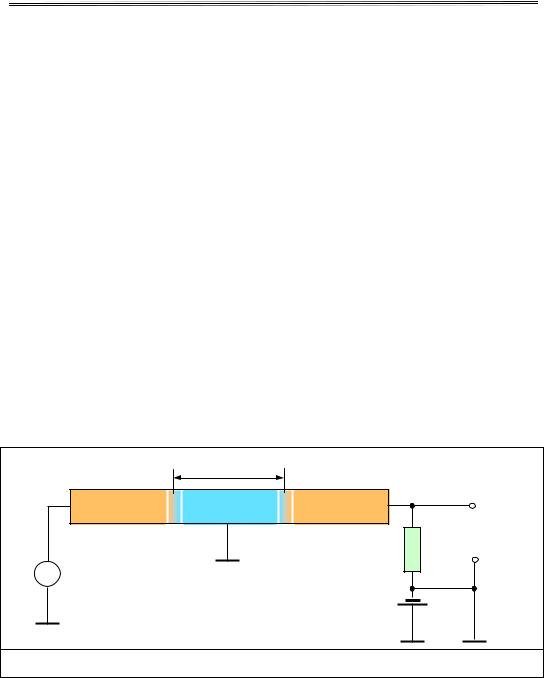
n-області. Як результат опір частини n-переходу, що безпосередньо примикає до p-n-переходу, знижується. Якщо концентрація неосновних носіїв при цьому залишається меншою від концентрації електронів, то загальна зміна опору n-області залишається невеликою, незважаючи на те, що концентрація дірок може збільшуватись на кілька порядків порівняно із рівноважною. Якщо в n-області поблизу p-n-переходу утворити ще один p-n-перехід, що включений у запірному напрямку, то струм через нього, який визначається концентрацією неосновних носіїв (дірок) різко зросте. Оскільки внутрішній опір p-n-переходу, що включений у зворотному напрямку, дуже великий, тобто струм через такий перехід є майже незмінним навіть за значної зміни напруги, то до електричного кола можна включити великий зовнішній опір Rн (рис. 14.22). Тоді за незначної зміни напруги, прикладеної до p-n-переходу, що включений у прямому напрямку, струм через другий p-n-перехід сильно змінюватиметься, та із включеного до кола зовнішнього опору можна знімати великі напруги. Це означає, що такий прилад (транзистор) можна використовувати як підсилювач електричних сигналів. Такий прилад, що складається із двох p-областей, які розділені n-областю, називають p-n-p-транзистором. Існують прилади, що мають іншу структуру – n-p-n-транзистори, а також велика кількість методів виготовлення транзисторів, зокрема вплавлення, дифузія та епітаксіальне нашарування. Наприклад, виготовлення транзистором методом дифузії проводиться шляхом одночасної дифузії до p-матеріалу донорної та акцепторної домішки, наприклад In і Sb.
|
|
d |
|
|
|
емітер (р) |
база (n) |
колектор (р) |
|
+ |
1 |
2 |
Rн |
|
|
|
|
||
~ |
Ve |
|
|
|
|
|
|
Vk |
+ |
|
|
|
|
|
|
|
Рис.14.22 |
|
|
Схема p-n-p–транзистора. „1” – емітерний p-n-перехід; „2” – колекторний p-n-перехід |
||||
У процесі виготовлення сурма дифундує швидше за індій та утворює |
||||
n-область. Концентрація індію береться істотно більшою за концентра- |
||||
цію сурми. Із цієї причини та область, до якої продифундував індій, |
||||
