1.3. Масса и импульс фотона

Итак, энергия фотона равна =. Воспользуемся законом взаимосвязи массы и энергии: , где – масса фотона. Отсюда:

где с – скорость света в вакууме. Фотон всегда движется со скоростью света, его масса покоя равна нулю.

Как всякая частица, фотон обладает массой, энергией и импульсом. Импульс фотона:

где λ – длина волны света в вакууме. Так как k = 2π/λ , то в векторной форме записи последнее выражение принимает вид:

Связь импульса фотона с его энергиейЕ_f получена из общей формулы теории относительности: для фотонаm₀ = 0 и

Импульс фотона – векторная величина, направление импульса совпадает с направлением распространения света, которое характеризуется волновым вектором .

Корпускулярные свойства фотона (энергия, импульс и масса) связаны с его волновой характеристикой – частотой света .

Экспериментальным подтверждением наличия у фотонов массы и импульса является существование светового давления. С квантовой точки зрения давление света вызвано тем, что при соударении с поверхностью тела каждый фотон передает этой поверхности свой импульс.

Лекция 3

1.4. Эффект Комптона

Комптон (1923) открыл явление, в кото­ром можно было наблюдать, что фотону присущи энергия и им­пульс. Результаты этого опыта — еще одно убедительное под­тверждение гипотезы Эйнштейна о квантовой природе самого электромагнитного излучения.

Комптон исследовал рассеяние жесткого рентгеновского из­лучения на образцах, состоящих из легких атомов, таких как графит, парафин и др. Схема его установки показана на рис. 1.14.

Источником рентгеновского излучения служила рентгенов­ская трубка с молибденовым антикатодом. Диафрагмы и D₂ выделяли узкий пучок монохромати­ческого рентгеновского излучения, который падал затем на исследуемый образец О. Для исследования спектрального состава рассеянного излуче­ния оно после прохождения ряда диа­фрагм попадало на кристалл К рент­геновского спектрографа, а затем в счетчик С (или на фотопластинку).

Комптон обнаружил, что в рассе­янном излучении, наряду с исходной длиной волны λ, появля­ется смещенная линия с длиной волны . Это получило на­звание комптоновского смещения, а само явление — эффекта Комптона.

Опыт показал, что наблюдаемое комптоновское смещение не зависит от материала рассеивающего образца и длины волны λ падающего излучения, а определяется лишь углом между направлениями рассеянного и падающего излучений (см. рис. 1.14). С увеличением угла интенсивность смещенной компоненты растет, а несмещенной — падает. Это показано на рис.1.15, где представлены результаты измерений на графите при различных углах рассеяния для так называемой К_a-линии молибдена, имеющей длину волны 0,071 нм. Слева показана форма линии исходного излучения (т. е. спектральное распределение интенсивности по длинам волн). Правее — то же самое для рассеянного излучения при различных углах рассеяния.

К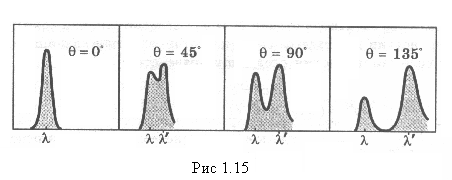лассическая теория оказаласьне в состоянии объяснить закономерности комптоновского рассеяния и в первую очередь появление смещенной компоненты. Они были поняты только на основе квантовой теории. Комптон предположил, что рассеяние рентгеновского кванта с измене­нием длины волны надо рассматривать как результат одиночного акта столкновения его с электроном.

В атомах легких элементов, с которыми проводились опыты, энергия связи электрона с атомом мала по сравнению с энергией, передаваемой электрону рентгеновским квантом при столкновении. Это выполняется тем лучше, чем больше угол рассеяния. В легких атомах энергией связи электрона внутри атома можно пренебречь при всех углах рассеяния, т. е. все электроны можно считать свободными. Тогда одинаковость комптоновского смещения для всех веществ сразу стано­вится понятной. Действительно, ведь с самого начала предпо­лагается, что рассеивающее вещество по существу состоит толь­ко из свободных электронов, т. е. индивидуальные особенности совсем не учитываются. Но это допустимо только для легких атомов. Для внутренних электронов тяжелых атомов такое представление не годится, что и подтверждает опыт.

Теперь рассмотрим столкновение фотона со свободным электроном с учетом того, что при этом должны соблюдаться законы сохранения энергии и импульса. Поскольку в результате столкновения электрон может стать релятивистским, этот процесс будем рассматривать на основе релятивистской динамики.

Итак, свет, переносящий энергию , обладает импульсоми может вести себя подобно частице. При фотоэффекте этот импульс передается всему образцу металла и испускаемому из него электрону. Импульс, переданный металлу, очень мал и не может быть измерен, однако при столкновении фотона со свободным электроном величину передаваемого импульса можно измерить.

Найдем связь длины волны рассеянного фотона с углом рассеяния и длиной волны фотона до соударения. Пусть на первоначально покоившийся свободный электрон с энергией покоя падает фотон с энергией и импульсом ε/с. После столкновения энергия фотона станет равной , а энергия и импульс электрона отдачи E' и p'. Согласно законам сохране­ния энергии и импульса системы фотон-электрон, запишем до и после столкновения следующие равенства:

, (1.9)

, (1.10)

где второе равенство записано на основе теоремы косинусов для треугольника импульсов (рис. 1.16).

Имея в виду, что связь между энергией и импульсом реляти­вистского электрона имеет вид

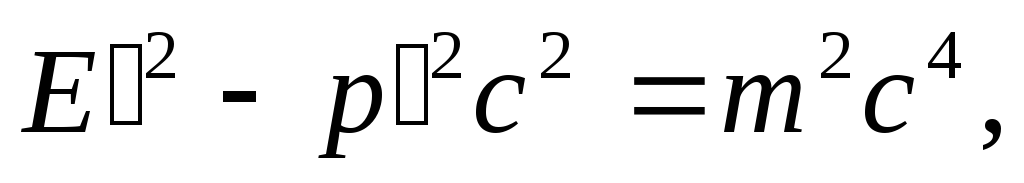(1.11)

найдем из формулы (1.9) и из (1.10):

(1.12)

(1.13)

Вычтя в соответствии с (1.11) выражение (1.13) из (1.12) и приравняв полученный результат m²c⁴, получим после сокращений:

. (1.14)

Учитывая, что , и, получим:

, (1.15)

где λ_c — комптоновская длина волны частицы массы т,

. (1.16)

Для электрона _c=2,43·10^-10см. Универсальная постоянная λ_c является одной из важнейших атомных констант. Соотношение (1.15) очень хорошо согласуется с наблюдаемой на опыте зависимостью комптоновского смещения от угла рассеяния θ (см. рис. 1.15). Уширение обеих компонент рассеянного излучения обусловлено движением электронов и атомов, на которых происходит рассеяние, т. е. эффектом Доплера.

Наличие несмещенной компоненты в рассеянном излучении обусловлено внутренними электронами атомов рассеивающего вещества. Их энергия связи, особенно в тяжелых атомах, сравнима с энергией рентгеновских фотонов, и, значит, такие электроны уже нельзя считать свободными. Обмен энергией и импульсом рентгеновского фотона происходит с атомом как целым. Масса же атома намного превышает массу электрона, поэтому комптоновское смещение фотонов, рассеянных на таких атомах, ничтожно, и их смещенная длина волны практи­чески совпадает с длиной волны падающего излучения. Это видно из формул (1.15) и (1.16).

С ростом атомного номера относительное число связанных электронов увеличивается. Поэтому должно происходить возрастание интенсивности несмещенной компоненты по сравнению с интенсивностью смещенной. Это и наблюдается на опыте.

Кроме того, с ростом угла рассеяния θ доля передаваемой электрону энергии возрастает. Отсюда следует, что при увели­чении угла рассеяния θ растет относительная доля электронов, которые можно считать свободными, а значит, растет и отноше­ние интенсивности смещенной компоненты к интенсивности несмещенной, что и показывает опыт.

Итак, чем больше энергия фотона, тем в меньшей степени проявляется связь электрона с атомом, тем больше электронов, которые можно считать свободными. Именно поэтому для на­блюдения эффекта Комптона нужно использовать жесткое рентгеновское излучение. Вот почему эффект Комптона не на­блюдается в видимой области спектра. Энергия соответствую­щих фотонов настолько мала, что даже внешние электроны атома не могут играть роль свободных.

О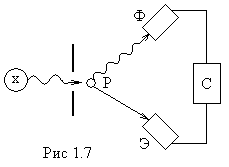пыты Боте и Гейгера(1925) доказали, что электрон отдачи и рассеянный фотон появляются одновременно. Схема опыта показана на рис. 1.17, где X — источник рентгеновского излучения, Р — рассеиватель, в котором под действием излучения происходит Комптон-эффект, Ф и Э — счетчики рассеянных фотонов и электронов отдачи. Эти счетчики установлены симметрично относительно рассеивателя Р и включены в схему совпадений С, т. е. в электрическую схему, которая позволяет регистрировать лишь те случаи, когда фотон и электрон в счетчиках Ф и Э появляются одновременно. В результате было установлено, что число одновременных регистраций фотона и электрона в счетчиках во много раз превосходит то число, которое можно было ожидать при случайном по времени появлении фотона и электрона. Так было доказано существование индивидуального столкновения фотона с электроном.

Рассмотрим обратный эффект Комптона. При столкновении с релятивистским электроном фотон рассеялся на угол θ, а электрон остановился. Найдем комптоновское смещение длины волны рассеянного фотона. Согласно закону сохранения импульса

,

где и — волновые векторы первоначального и

рассеянного фотонов, — импульс электрона (рис.1.18). Изэтого рисунка согласно теореме косинусов имеем

, (1.17)

где учтено, что ;, и — энергия фотона до и по­сле рассеяния.

На основании закона сохранения энергии запишем ,

где Е – полная энергия электрона, m – его масса покоя. Из этого равенства

найдем

. (1.18)