Лекция 8

5. Стационарные задачи квантовой механики

5.1.Частица в потенциальном ящике с бесконечно высокими стенками

Рассмотрим частицу, находящуюся в бесконечно глубокой одномерной потенциальной яме. Будем считать, что частица может двигаться только в направлении оси ОХ. Стенки ямы бесконечно высокие и представляют собой параллельные плоскости (рис.5.1). Такую прямоугольную яму называем ящиком. Она является упрощенной моделью атома водорода, в котором движется электрон. Потенциальная энергия частицы

в ящике равна нулю, а за пределами

ящика . Уравнение Шредингера Шредингера для такой частицы имеет вид:

.

B ящике U=0, поэтому .

Обозначим

. (5.1)

Тогда

.

Это известное из теории колебаний уравнение синусоидальной волны, причем k , определяемое уравнением (1) – волновое число. Решение этого уравнения имеет вид:

. (5.2)

При решении уравнения Шредингера должны выполняться граничные условия:

- так как стенки ящика бесконечно высокие, то вероятность обнаружить частицу за пределами ящика равна нулю =0. Однако - непрерывная функция, следовательно, на границах ящика также должна обращаться в ноль: , тогда и ; на правой границе ящика , поэтому n=1, 2…. Отсюда

. (5.3)

При n=0 и - вероятность обнаружить частицу хотя бы в какой-то точке пространства равна нулю, т.е. частица нигде не находится. Такого быть не может, поэтому значение п=0 лишено физического смысла..

Условие (5.3) означает что волновое число k может принимать только некоторые разрешенные значения в зависимости от целого числа п , т.е. квантуется. Из условия (5.3) также следует, что по дну ящика должно укладываться целое число полуволн де Бройля, что совпадает с условием возникновения стоячих волн в струне.

Действительно, подставим в уравнение (5.3), имеем:

; и .

Пусть частица летит к стенке ящика (рис.5.2). Справа от стенки происходит наложение двух волн де Бройля, соответствующих частице – прямой и отраженной, распространяющихся в противоположных направлениях. Стенка абсолютно отражающая, поэтому амплитуда падающей волны равна амплитуде отраженной волны, и в ящике образуется стоячая волна.

Импульс частицы равен , тогда согласно (5.3) имеем:

- импульс частицы в ящике принимает дискретные значения в соответствии с целым числом п, т.е. квантуется.

Подставим (5.3) в (5.1) , имеем:

, n=1,2… (5.4)

- энергия частицы в ящике принимает ряд дискретных значений (квантуется).

В теории колебаний доказывается, что уравнение Шредингера имеет решение не при любых значениях энергии, а лишь при избранных, которые называются собственными значениями энергии. Выражение (5.4) как раз и определяет эти значения. Каждой такой энергии отвечает стационарное состояние системы, т.е. такое, в котором распределение вероятностей обнаружить частицу не меняется. Решения, соответствующие собственным значениям , называются собственными функциями задачи. Наименьшее значение энергии достигается при n=1:

.

Это энергия основного состояния. В квантовой механике частица не может иметь энергию, меньшую . С ростом n энергия растет. Вычислим расстояние между энергетическими уровнями:

С ростом n расстояние между уровнями увеличивается (рис.5.3).

Для молекулы газа в сосуде , энергетические уровни расположены так близко, что практически неразличимы, спектр можно считать сплошным.

Для свободного электрона и эВ. Для электрона в атоме , - дискретность уровней весьма заметна.

Подставив k из (5.3) в решение уравнения Шредингера (5.2), найдем собственные функции задачи:

Для определения амплитуды а воспользуемся условием нормировки:

На концах промежутка интегрирования подынтегральная функция обращается в 0. Поэтому значение интеграла получим, умножив среднее значение на длину промежутка . Имеем: тогда собственные функции:

Н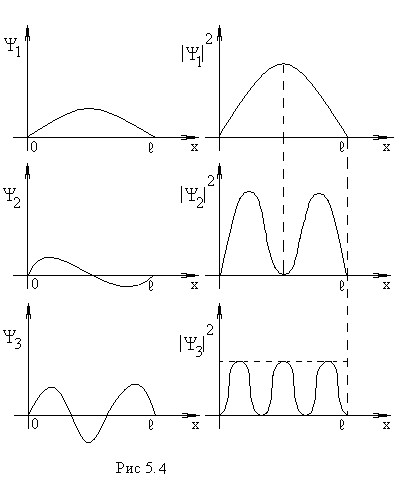а рисунке 5.4 показаны зависимости и для частицы при n=1 и n=2. При n=1 вероятность обнаружить частицу в яме максимальная, а по краям ямы – равна нулю. При n=2 частица не может быть обнаружена в середине ямы, однако она одинаковое число раз бывает в левой и правой частях.

Электрон, заключенный в ящике, является лишь очень грубой моделью атома водорода. Реальная яма является трехмерной, электрон в атоме находится в поле кулоновских сил, поэтому стенки ямы имеют вид, представленный на рисунке 5.5. Однако поведение электрона в обеих ямах практически одинаково и описывается стоячей волной, которой соответствуют собственные значения энергии

Рассмотренная задача показывает, что движение квантовой частицы отличается от движения классической частицы тем, что:

1. нельзя говорить о точном местонахождении частицы в яме, а можно говорить лишь о вероятности нахождения её в той или иной точке. Эта вероятность определяется величиной .

2. Энергия квантовой частицы квантуется, т.е. принимает ряд дискретных значений ….

3. Импульс квантовой частицы квантуется.