11.3.Схемы накачки

Рассмотрим процессы получения в данной среде инверсной населенности. На первый взгляд может показаться, что инверсию можно создать при взаимодействии среды с достаточно мощной электромагнитной волной частоты , которая будет индуцировать переходы атомов среды, удовлетворяющие выражению:

.

Действительно, при термодинамическом равновесии уровень n заселен больше, чем уровень m, т.е. под действием падающей волны происходит больше переходов n  m, чем m  n, и можно надеяться осуществить таким путем инверсную населенность.

Однако такой механизм работать не будет. Когда наступят условия, при которых населенности уровней окажутся одинаковыми (), процессы вынужденного излучения и поглощения начнут компенсировать друг друга, и среда станет прозрачной для электромагнитной волны частоты  ( волна проходит, не изменяя интенсивности ). В такой ситуации говорят о двухуровневом насыщении.

Таким образом, используя только два уровня, невозможно получить инверсию населенностей. Для этой цели используют трехуровневые и четырехуровневые схемы лазеров.

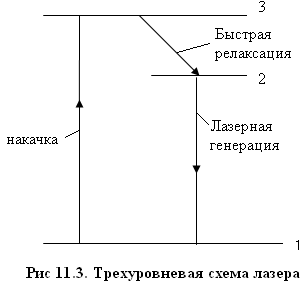
В трехуровневом лазере (рис.11.3) атомы каким-либо способом переводятся с основного уровня 1 на уровень 3. Если выбрана среда, в которой атом, оказавшийся в возбужденном состоянии на уровне 3, быстро переходит на уровень 2, то в такой среде можно получить инверсию населенностей между уровнями 2 и 1.

В четырех уровневом лазере (рис.11.4) атомы также переводятся с основного уровня ( будем называть его нулевым ) на уровень 3. Если после этого атомы быстро переходят на уровень 2, то между уровнями 2 и 1 может быть получена инверсная заселенность. Когда в таком четырехуровневом лазере возникает генерация, атомы в процессе вынужденного излучения переходят с уровня 2 на уровень 1. Поэтому для непрерывной работы четырехуровневого лазера необходимо, чтобы частицы, оказавшиеся на уровне 1, очень быстро переходили на нулевой уровень. В четырехуровневом лазере инверсию получить гораздо легче. Действительно, разности уровней между рабочими уровнями лазера много больше kТ, и в согласно статистике Больцмана почти все атомы при термодинамическом равновесии находятся в основном состоянии. Обозначим число атомов в единице объема среды через N_t. В случае трехуровневой системы эти атомы первоначально находятся на уровне 1. Переведем теперь атомы с уровня 1 на уровень 3. Тогда с этого уровня атомы будут релаксировать с переходом на более низкий уровень 2. Если такая релаксация происходит достаточно быстро, то уровень 3 остается практически незаселенным. Для того, чтобы населенности уровней 1 и 2 сделать одинаковыми, на уровень 2 нужно перевести половину атомов N_t, расположенных первоначально на основном уровне. Инверсию населенности будет создавать любой атом, переведенный на верхний уровень сверх этой половины от общего числа атомов. Однако в четырехуровневом лазере, поскольку уровень 1 первоначально был также незаселенным, новый атом, оказавшийся в возбужденном состоянии, будет давать вклад в инверсию населенностей.

Если верхний уровень накачки пуст, то скорость, с которой верхний лазерный уровень 2 станет заселяться с помощью накачки, в общем случае равна

(dN₂/dt)_p = W_pN_n

N_n – населенность основного уровня; W_p – скорость накачки.