8.6.Векторная модель атома

При построении такой модели механические и магнитные моменты атома изображаются в виде направленных отрезков. Строго говоря, вследствие неопределенности направлений векторов в пространстве такой прием не является правомерным. Поэтому такая модель условна.

Пусть и М_z имеют определенные значения (М_х и М_у при этом не определены, т.к. неопределено направление в пространстве). В таком случае векторможет иметь направление одной из образующих конуса (рис. 8.2). Можно считать, что векторравномерно вращается вокруг направленияz, совпадающего с осью конуса.

Допустим, что в направленииz создано магнитное поле . С механическим моментомсвязан магнитный момент. Поэтому черезполе воздействует на. Скорость прецессии (вращения) моментавокругбудет тем больше, чем больше В. Согласно правилам построения векторной модели складываемые моментыипрецессируют вокруг направления результирующего момента(рис.8.3). Моменты взаимодействуют друг с другом (через магнитные моментыи). Скорость прецессии предполагается пропорциональной интенсивности взаимодействия.

Всостоянии, в котором определеныМ и М_z, вектор прецессируем вокруг направленияz. Если по оси z создать магнитное поле, будут наблюдаться разные явления в зависимости от соотношения между взаимодействиями моментов друг с другом и с магнитным полем. Рассмотрим два случая:

1) слабое поле – взаимодействие моментов друг с другом больше, чем воздействие поля на каждый момент;

2) сильное поле – действие поля на каждый из моментов превосходит действие их между собой.

В первом случае моменты складываются между собой в результирующий момент , который проектируется на направление поля (рис. 8.4).

П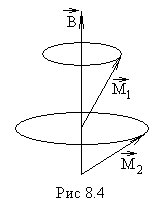ри этом происходят два вида прецессии:

- прецессия моментов ивокруг направления,

- прецессия результирующего вектора вокруг направления.

Скорость первой прецессии будет гораздо больше, так как взаимодействие моментов между собой превосходит воздействие на каждый из них магнитного поля.

Во втором случае поле разрывает связь между моментамии, и каждый из них прецессирует вокруг направления поля независимо от другого. Проектироваться на направление поля векторыибудут тоже каждый в отдельности (рис.8.5).

Найдем суммарный магнитный момент атома, пользуясь векторной моделью атома.

Изобразим на рис.8.6 векторы ,,, соответствующиеивекторыибудем изображать отрезками одинаковой длины. Векторв два раза больше, чем(из-за удвоенного магнетизма спина). Поэтому векторнеколлиниарен вектору.

Векторы ипрецессируют вокруг направления, вовлекая в эту прецессию и результирующий вектор магнитного момента.

За достаточно большое время наблюдения можно зарегистрировать среднее значение вектора, это.

Найдем проекцию этого вектора на направление (рис.8.6):

.

но

;

.

Значение найдем из соотношения . Возведем его в квадрат:

,

отсюда

.

Значение найдем следующим образом:

тогда

или

мы получили значение, которое было получено ранее без векторной модели.

Таким образом, рассмотренная векторная модель, несмотря на ограниченность, связанную с ее целостностью, правильно описывает ряд процессов, протекающих в атоме.

ЛЕКЦИЯ 13