
- •1.Тепловое излучение
- •1.1.Закон Кирхгофа
- •1.2.Законы теплового излучения абсолютно чёрного тела
- •1.2.Фотоэффект
- •1.3. Масса и импульс фотона
- •1.4. Эффект Комптона
- •Теперь воспользуемся равенством . Вычтем (1.17) из (1.18). В результате после сокращений получим:
- •Или Отсюда
- •1.5.Тормозное рентгеновское излучение
- •1.6. Корпускулярно-волновой дуализм света
- •2.Двойственная корпускулярно-волновая природа частиц вещества
- •2.1. Гипотеза де Бройля
- •2.2Свойства волн де Бройля
- •3. Элементы квантовой механики
- •3.1.Волновая функция
- •3.2. Принцип неопределенности
- •3.3.Уравнение Шредингера
- •4. Атом Резерфорда - Бора
- •4.1.Ядерная модель атома
- •4.2.Постулаты Бора. Опыты Франка и Герца
- •4.3.Боровская модель атома водорода
- •Согласно 2-му закону Ньютона (4.13)
- •Тогда постоянная Ридберга
- •6. Операторы физических частиц
- •6.1 Линейные операторы. Собственные функции и
- •6.3. Законы сохранения физических величин в
- •6.4.Четность, закон сохранения четности
- •5. Стационарные задачи квантовой механики
- •5.1.Частица в потенциальном ящике с бесконечно высокими стенками
- •5.2.Движение частицы в потенциальном ящике конечной глубины
- •5.3.Прохождение частицы через потенциальный барьер
- •Лекция 9-10
- •8.2. Ширина спектральных линий
- •Средняя энергия подачи:
- •8.4.Полный механический момент многоэлектронного атома
- •8.5.Магнитный момент атома
- •8.6.Векторная модель атома
- •9. Механика системы микрочастиц
- •9.1.Волновая функция системы микрочастиц
- •Можно показать, что четность состояния системы частиц равна произведению четностей состояния отдельных частиц:
- •9.2. Тождественность частиц одного и того же вида и принцип Паули
- •Лекция 14
- •9.4.Многоэлектронные атомы
- •9.5.Эффекты Зеемана и Штарка
- •9.5.Рентгеновские спектры
- •10. Двухатомная молекула
- •10.1. Ионная и ковалентная связь. Молекула водорода. Обменный интеграл
- •10.1.Молекулярные спектры
- •Лекция 16
- •11.Генераторы когерентного света
- •На рис. 11.1 представлена диаграмма энергетических уровней, причем длина горизонтальной черты определяет населенность того или иного энергетического уровня.
- •11.2. Принцип действия лазеров
- •11.3.Схемы накачки
- •11.4.Классификация лазеров
Лекция 1.
1.Тепловое излучение
1.1.Закон Кирхгофа
Тепловое излучение – это испускание электромагнитных волн за счёт внутренней энергии тел. Тепловое излучение имеет место при любой температуре. При низких температурах оно сдвинуто в длинноволновую часть спектра.
Излучение будет равновесным, если распределение энергии между телом и излучением не меняется для каждой длины волны. Способность теплового излучения быть в равновесии вызвана тем, что интенсивность этого излучения возрастает с температурой.
Поток энергии, испускаемый единицей поверхности излучающего тела по всем направлениям (в пределах телесного угла 2π) называется энергетической светимостью тела R. Энергетическая светимость – функция температуры.
Излучение
включает в себя волны различных частот
ω
(длин волн λ).
Пусть поток энергии, испускаемый единицей
поверхности тела в интервале частот
dω,
равен
![]() .
Значение
.
Значение
![]() мало поэтому
мало поэтому
![]() ,
(1.1),
,
(1.1),
величина
![]() называется испускательной способностью
тела. Это мощность излучения с единицы
площади поверхности тела в интервале
частот единичной ширины. Испускательная
способность
называется испускательной способностью
тела. Это мощность излучения с единицы
площади поверхности тела в интервале
частот единичной ширины. Испускательная
способность
![]() есть
функция частоты излучение и температуры.
есть
функция частоты излучение и температуры.
Энергетическая светимостъ тела связана с его испускательной способностью формулой
![]() .
.
Излучение
можно характеризовать вместо частоты
длиной волны
![]() .
Участку спектра
.
Участку спектра
![]() соответствует интервал длин волн
соответствует интервал длин волн
![]() ,
причем
,
причем![]() ,
тогда, дифференцируя, получаем
,
тогда, дифференцируя, получаем
![]() .
.
Знак
минус в этом выражении не имеет
существенного значения, он лишь
показывает, что с ростом
![]() длина волны
длина волны
![]() убывает.
Поэтому минус в дальнейшем писать не
будем.
убывает.
Поэтому минус в дальнейшем писать не
будем.
Доля
энергетической светимости, приходящаяся
на интервал
![]() равна
равна
![]() .
.
Так
как интервалы
![]() и
и
![]() относятся к одному и тому же участку
спектра, величины
относятся к одному и тому же участку
спектра, величины
![]() и
и
![]() должны совпадать, т.е.
должны совпадать, т.е.
![]() ,
или
,
или
![]() ,
,
и
![]() .
(1.2)
.
(1.2)
с
помощью формулы (1.2) можно перейти от
![]() к
к
![]() и
наоборот.
и
наоборот.
Все тела в той или иной степени поглощают энергию падающих на них электромагнитных волн. Спектральной характеристикой поглощения является поглощательная способность тела (коэффициент монохроматического поглощения)
![]()
 ,
,
dФω
-
падающий на тело поток электромагнитной
энергии, dФω`-
часть потока, которую поглотило тело,
![]() есть функция частоты излучения и его
температуры (
есть функция частоты излучения и его
температуры (![]() 1).
1).
Если
тело полностью поглощает падающую на
него энергию (![]() =
1), оно называется абсолютно чёрным.
Тело, поглощательная способность
которого не зависит от частоты и при
фиксированной температуре имеет
постоянное и меньшее единицы значение,
называется серым, т.е.
=
1), оно называется абсолютно чёрным.
Тело, поглощательная способность
которого не зависит от частоты и при
фиксированной температуре имеет
постоянное и меньшее единицы значение,
называется серым, т.е.
![]() =
=
![]() ,
,
![]() =const<1.
=const<1.
При
равновесном излучении выполняется
правило Прево: если два тела поглощают
разные количества энергии, то и излучения
у них тоже будут различны. Чем больше
испускательная способность тела
![]() ,
тем больше его поглощательная способность
аωT.
,
тем больше его поглощательная способность
аωT.
Закон Кирхгофа утверждает, что отношение испускательной и поглощательной способностей не зависит от природы тела, оно является для всех тел одной и той же (универсальной) функцией частоты (длины волны) и температуры:
![]() ,
,
![]() –универсальная
функция Кирхгофа. Для абсолютно чёрного
тела
–универсальная
функция Кирхгофа. Для абсолютно чёрного
тела ![]() =1, поэтому
=1, поэтому
![]() =
=
![]() ,
таким образом,
,
таким образом, ![]() есть испускательная способность
абсолютно чёрного тела.
есть испускательная способность
абсолютно чёрного тела.
При
теоретических исследованиях для
характеристики спектрального состава
равновесного теплового излучения
удобнее пользоваться функцией частоты
![]() .
В экспериментальных работах предпочтительнее
пользоваться функцией
.
В экспериментальных работах предпочтительнее
пользоваться функцией ![]() ,
при этом
,
при этом
![]()
Тогда
![]() и
и ![]() .
.
Абсолютно
чёрных тел в природе не существует.
Некоторые тела при определённых условиях
близки к чёрному. Излучение Солнца
можно считать близким к излучению
абсолютно чёрного тела. Чёрная бумага
поглощает 96% падающей на неё энергии,
сажа - 98%, чёрный бархат – 99,6%. Сажа,
платиновая чернь имеют
![]() ,
близкую к 1 лишь в ограниченном интервале
частот. В инфракрасной области
,
близкую к 1 лишь в ограниченном интервале
частот. В инфракрасной области
![]() <<1.
<<1.
Однако
можно создать устройство, имеющее ![]() = 1. Это почти
замкнутая полость, имеющая малое
отверстие (рис.1.1). Излучение проникает
внутрь через отверстие,
= 1. Это почти
замкнутая полость, имеющая малое
отверстие (рис.1.1). Излучение проникает
внутрь через отверстие, 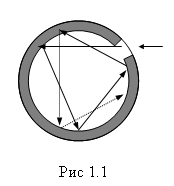 претерпевая
многократные отражения. При каждом
отражении часть энергии поглощается.
Таким образом, всё излучение полностью
поглощается, и из полости выходит
излучение,cоответствующее
по спектральному составу излучению
абсолютно чёрного тела при
претерпевая
многократные отражения. При каждом
отражении часть энергии поглощается.
Таким образом, всё излучение полностью
поглощается, и из полости выходит
излучение,cоответствующее
по спектральному составу излучению
абсолютно чёрного тела при 
 определённой температуре. По этому
излучению можно найти экспериментально
вид функцииf(ω,T)
или φ (λ,T)
(рис. 1.2).
определённой температуре. По этому
излучению можно найти экспериментально
вид функцииf(ω,T)
или φ (λ,T)
(рис. 1.2).
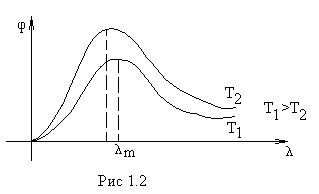 Для
каждой кривой имеет место максимум. Это
свидетельствует о том, что энергия
распределена по спектру абсолютно
чёрного тела неравномерно – в области
очень малых и очень больших частот
абсолютно чёрное тело почти не излучает
энергию. С ростом температуры максимум
сдвигается в область меньших длин волн.
Площадь, ограниченная кривой
Для
каждой кривой имеет место максимум. Это
свидетельствует о том, что энергия
распределена по спектру абсолютно
чёрного тела неравномерно – в области
очень малых и очень больших частот
абсолютно чёрное тело почти не излучает
энергию. С ростом температуры максимум
сдвигается в область меньших длин волн.
Площадь, ограниченная кривой
![]() ,
пропорциональна энергетической
светимости RωT
при данной температуре и растет с ростом
температуры.
,
пропорциональна энергетической
светимости RωT
при данной температуре и растет с ростом
температуры.
Рассмотрим
излучение, находящееся в равновесии с
веществом. Для этого представим себе
изолированную полость, стенки которой
поддерживаются при постоянной температуре
Т.
В равновесном состоянии энергия
излучения будет распределена в объеме
полости с определенной плотностью ![]() .
Спектральное распределение этой энергии
можно охарактеризовать функцией
.
Спектральное распределение этой энергии
можно охарактеризовать функцией ![]() ,
определяемой условием
,
определяемой условием ![]() ,
где
,
где ![]() -
доля плотности энергии, приходящаяся
на интервал частот
-
доля плотности энергии, приходящаяся
на интервал частот ![]() .
Полная плотность энергии равна
.
Полная плотность энергии равна
![]()
Равновесная
плотность энергии излучения ![]() зависит
только от температуры и не зависит от
свойств полости.
зависит
только от температуры и не зависит от
свойств полости.
 Найдем
связь равновесной плотности энергии
излучения
Найдем
связь равновесной плотности энергии
излучения ![]() с
энергетической светимостью абсолютно
черного тела
с
энергетической светимостью абсолютно
черного тела ![]() .
Рассмотрим эвакуированную полость с
абсолютно черными стенками. В случае
равновесия через каждую точку внутри
полости будет проходить в любом
направлении поток излучения одинаковой
плотности. Если бы излучение
распространялось в одном заданном
направлении (т.е. через данную точку
проходил только один луч), плотность
потока энергии в рассматриваемой точке
была бы равна произведению плотности
энергии и
на скорость электромагнитной волны с.
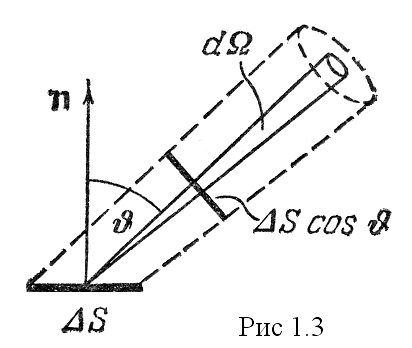
Однако
через каждую трубку (рис.1.3) проходит
множество лучей, направления которых
равномерно распределены в пределах
телесного угла 4
.
Рассмотрим эвакуированную полость с
абсолютно черными стенками. В случае
равновесия через каждую точку внутри
полости будет проходить в любом
направлении поток излучения одинаковой
плотности. Если бы излучение
распространялось в одном заданном
направлении (т.е. через данную точку
проходил только один луч), плотность
потока энергии в рассматриваемой точке
была бы равна произведению плотности
энергии и
на скорость электромагнитной волны с.
Однако
через каждую трубку (рис.1.3) проходит
множество лучей, направления которых
равномерно распределены в пределах
телесного угла 4![]() .
Поток энергии
.
Поток энергии ![]() также распределен равномерно в пределах
этого телесного угла. Следовательно, в
каждой точке в пределах телесного угла
также распределен равномерно в пределах
этого телесного угла. Следовательно, в
каждой точке в пределах телесного угла
![]() будет течь поток энергии, плотность
которого
будет течь поток энергии, плотность
которого
![]() .
.
Возьмем
на поверхности полости элементарную
площадку ![]() .
Эта площадка посылает в пределах
телесного угла
.
Эта площадка посылает в пределах
телесного угла ![]() в направлении, образующем с нормалью
угол
в направлении, образующем с нормалью
угол ![]() ,
поток энергии
,
поток энергии ![]() .
.
По
всем направлениям в пределах телесного
угла 2![]() ,
площадка посылает поток энергии
,
площадка посылает поток энергии

Однако
![]() ,
тогда
,
тогда
![]() .
.
Это равенство должно выполняться для каждой спектральной составляющей излучения. Тогда
![]()
