источники и стоки функции распределения, мощность которых определяется столкновениями между молекулами.
В альтернативном |
предельном случае |
λ 1 r0 , τ* ≤ τ0 характер |
движения иллюстрирует |
рис. 6.5б. Очевидно, |
в случае плотных газов |
(n <r0−3 ) понятие «столкновение» теряет смысл, так как молекула все время
находится внутри сферы действия соседних молекул.
6.3.2. Уравнение непрерывности в отсутствие столкновений. Перейдем к изучению процессов в разреженных газах (приближение Больцмана, учитываются только попарные столкновения). Передвигаясь по фазовым траекториям, изобразительные точки распределены
в µ-пространстве с |
плотностью |
f r(t),v(t),t . |
В |
последующий момент |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
времени |
t +∆t |
функция |
распределения |
примет |
значение |
|
|
|
(r′,v′,t |
+ ∆t). |
Выберем |
промежуток |
f r(t +∆t),v(t +∆t),t +∆t ≡ f1 |
|
|
|
|
|
|
|
|
времени ∆t |
значительно большим, чем время столкновения (∆t >> τ0 ). С |
другой стороны считаем ∆t малым по |
сравнению |
со средним временем |
между столкновениями (∆t << τ* ), т.е. путь, пройденный частицей за это время будет намного меньшим, чем средняя длина свободного пробега. Иными словами, характер движения частицы в этот промежуток времени определяется координатами r(t), скоростью v(t) в предыдущий момент
времени и внешними силами F :
r′ = r(t +∆t) r(t) + ∂∂rt ∆t = r(t) +v∆t ; v′ = v(t +∆t) v(t) + ∂∂vt ∆t = v(t) + mF ∆t .
Здесь предполагается, что система однородная, а сила F не зависит от координат пространства. В этих условиях число изобразительных точек в
элементе объема drdv не меняется, т.е. f1
виде ряда
=f . Представляя f1 (r′,v′,t +∆t) в
+F ∂f ∆t , m ∂v
приходим к уравнению непрерывности, которое определяет дрейфовую
производную |
|
|
|
|
|
|
|
|
|
|
|
|
|
∂f |
|
F |
|
∂f |
|
|
|
|
∂f |
= −v |
− |
|
|
∂f |
(6.19) |
|
|
|
|
|
≡ |
. |
|
|
|
∂r m ∂v |
|
|
|
|
∂t |
|
|
∂t d |
|
Второе слагаемое в правой части уравнения отлично от нуля только в том случае, если газ помещен во внешнее поле.
6.3.3. Учет столкновительных процессов . Столкновения между молекулами приводят к скачкообразному изменению проекций скорости (при неизменных координатах) и, следовательно, к скачкообразному перемещению изобразительных точек. В этом приближении они «гибнут» в одних частях µ-пространства и «рождаются» в других не пересекая границ выделенного объема drdv . Это значит, что приближение «мгновенных» столкновений вынуждает ввести в правую часть уравнения непрерывности источники и стоки молекул данной скорости в данной точке пространства.
Поэтому общее изменение функции f |
во времени можно представить суммой |
|
|
|
|
|
|
|
|
|
|
∂f |
|
|
∂f |
|
|
|
|
|
|
|
|
|
∂f |
|
|
|
|
. А (6.19) |
дрейфовой и столкновительной производных |
|
|
= |
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂t |
|
|
|
|
|
|
|
|
|
∂t |
∂t d |
|
c |
должно быть заменено уравнением |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂f |
+v ∂f |
+ F |
∂f |
= St = q |
ист |
−q |
ст |
, |
|
|
|
|
(6.20) |
|
|
∂t |
∂r |
m |
∂v |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂f |
называют еще и интегралом столкновений (stoss |
|
integral), а |
где St ≡ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂t c |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
величины qист , qст представляют собой мощности источников и стоков – числа
263
частиц со скоростью v в точке r , появляющиеся и исчезающие за единицу времени в единице объема и отнесенные к единичному интервалу скоростей.
Опишем физическую основу вычисления St. Рассмотрим столкновения молекул, из которых одна имеет скорость в интервале (v,v +dv ), а другая – в
интервале (v′,v′ +dv′). После соударения молекулы приобретают скорости,
лежащие в интервалах (v,v +dv ) и (v′,v′ +dv′), соответственно. Число таких
столкновений за единицу времени в единичном объеме пропорционально
числам сталкивающихся молекул со скоростями |
( |
+dv |
) |
( |
|
|
|
) |
и |
v,v |
|
v′,v′ +dv′ |
|
интервалам значений скоростей после удара d3v и d3v′ (здесь d3v ≡ dv |
dv dv |
z |
, |
|
|
|
|
|
|
|
|
x |
y |
|
|
в общем случае d3η – элементарный объем в |
соответствующем фазовом |
пространстве η = (v, p)). Таким образом, это число можно записать в виде |
|
|
|
P (v,v′ |
|
v,v′) f f ′ d3vd3v′d3vd3v′, |
|
|
P (v,v′ |
|
v,v′) |
|
|
|
|
|
|
|
|
где для краткости обозначено f = f (r,v,t), f ′ = f (r,v′,t), |
|
– |
|
плотность вероятности соударения v,v′ → v,v′, |
зависящая |
от скоростей |
обеих молекул до и после удара. Полное число соударений, испытываемых молекулами со скоростями в интервале (v,v +dv ) за единицу времени в
единице объема, вычисляется интегрированием по всем значениям v′, v , v′. При малом интервале dv это и определяет убыль числа молекул с указанными скоростями (v,v +dv ). Таким образом, мощность стоков равна
qст = ∫∫∫ P (v,v′ v,v′) f f ′ d3v′d3vd3v′.
Наряду с процессами v,v′ → v,v′, приводящими к уменьшению числа молекул со скоростью v , в газе происходят и обратные процессы v,v′ → v,v′,
которые увеличивают их число. Они порождают источники с мощностью
264
qист = ∫∫∫ P (v,v′ v,v′) f f ′ d3v′d3vd3v′,
где P (v,v′ v,v′) – плотность вероятности перехода v,v′ → v,v′, f = f (r,v,t),
f ′ = f (r,v′,t). Первый аргумент функции распределения r одинаков во всех
функциях, т.к. при ударе координаты в приближении мгновенных соударений не изменяются. Считая функцию плотности вероятности соударений симметричной по отношению к перестановке аргументов начального и конечного аргументов
P (v,v′ v,v′)= P (v,v′ v,v′), дляинтеграластолкновенийимеем
St = qист −qст = ∫∫∫ P (v,v′ v,v′) (ff ′− ff ′) d3v′d3vd3v′. (6.21)
Определение функции P (v,v′ v,v′) можно найти, например, в книгах: Ю.Б.
Румер, М.Ш. Рывкин Термодинамика. Статистическая физика и кинетика. М. 1972, § 67; Л.В. Радушкевич Курс статистической физики. М. 1966, § 7. Для классических систем в предположении, что атомы газа – абсолютно твердые сферы с диаметрами d
St = |
d2 |
|
|
′ |
−v |
|
cos θ (ff |
′ |
′ |
3 ′ |
(6.22) |
|
|
2 |
∫∫∫ |
|
v |
|
|
− ff |
)d v dΩ. |
|
|
|
|
|
|
|
|
|
Здесь θ – угол между векторами (v′−v) и (v −v), dΩ – элемент телесного угла.
После подстановки (6.21) в (6.20) получаем интегро-дифференциальное уравнение для неравновесной функции распределения
∂∂ft +v ∂∂rf + mF ∂∂vf = ∫∫∫ P (v,v′ v,v′) (ff ′− ff ′) d3v′d3vd3v′, (6.23)
которое называется кинетическим уравнением Больцмана. Вывод этого уравнения, идея которого принадлежит Больцману, нельзя считать строгим. Здесь предполагается, во-первых, что изменение по времени функции f = f (r,v,t) аддитивно относительно двух процессов, имеющих различное
происхождение, а именно: потоки газа вследствие наличия градиентов
265
плотности и внешних полей и столкновения. Иными словами, предполагается, что потоки и соударения не влияют друг на друга. Вовторых, приближение Больцмана учитывает только попарные столкновения частиц. В третьих, в интеграле столкновений значения функций f , f ′, f , f ′
берутся в одной и той же точке пространства r , в то время как с учетом конечных размеров молекул координаты в функциях f и f ′ и в функциях f
и f ′ должны быть выбраны различными.
6.4. Приближение времени релаксации
6.4.1. Упрощенное уравнение Больцмана . Кинетическое уравнение Больцмана содержит максимальную информацию о макроскопическом движении разреженного газа. Оно учитывает столкновения молекул, действие внешних полей, наличие градиентов температуры, давления, плотности и т.п. Однако общее решение такого типа интегро-дифференциального уравнения связано с весьма серьезными трудностями. Существует ряд приближенных методов, основанных, в частности, на представлении решения в виде рядов, а также на упрощающих физических предположениях.
Интеграл столкновений существенно упрощается, если столкновениями частиц газа друг с другом пренебречь. В этом случае эволюция состояния газа определяется столкновениями его частиц с частицами другого сорта. Такими частицами могут быть молекулы или атомы примеси, ионы кристаллической решетки и т.д. Предполагается, что столкновения упругие, происходят без передачи энергии, так что абсолютное значение скорости частицы до и после столкновения не меняются. При этих условиях интеграл столкновения заменяется выражением
St = − fτ−(v)f0 ,
а кинетическое уравнение Больцмана принимает вид
∂f |
+v |
∂f + F |
∂f |
= − |
f − f0 |
. |
(6.24) |
∂t |
∂v |
|
|
∂r m |
|
τ(v) |
|
Здесь τ(v) – время релаксации, зависящее от абсолютного значения скорости частиц, f0 – равновесная функция распределения.
6.4.2. Электропроводность электронного газа . Кинетическое уравнение Больцмана для электронного газа в металлах в виде (6.24) отличается от (6.23) следующими особенностями. Во-первых, в (6.24) учитываются только столкновения электронов с ионами решетки, ионы моделируются твердыми шарами; во-вторых, поскольку ионы гораздо тяжелее электронов, можно считать, что при упругих соударениях передается только импульс, но практически не передается энергия. Очевидно, последнее строго не выполняется, так как электроны участвуют в установлении равновесия. Однако в первом приближении закон сохранения энергии по сравнению с законом сохранения импульса можно не принимать во внимание. Эти условия никак не отражаются на левой части уравнения (6.23).
Если градиенты и внешние поля после их включения (t ≥t0 ) остаются постоянными во времени, электронный газ за время релаксации приходит в стационарное состояние. Ввиду большого числа столкновений время его
установления очень малое (~ 10−9 |
с). Без учета релаксационных процессов |
( ∂f ∂t = 0 )уравнение |
для |
|
функции |
распределения, согласно |
(6.24), |
принимает вид |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂f |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ |
|
F ∂f |
, |
(6.25) |
f (r,v) = f0(r,v) −τ(v) v |
∂r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m ∂v |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2m |
3 |
|
2m |
3 |
ε(v)−µ(r ) |
−1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
kT |
|
|
|
|
f |
= |
|
|
|
f ′ = |
|
|
|
e |
|
|
|
+1 |
|
(6.26) |
|
3 |
|
|
3 |
|
|
|
|
|
0 |
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
h |
|
|
|
h |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
нормированная равновесная функция электронного газа.
Малое отклонение функции распределения от ее равновесного значения представим через вектор η(v), зависящий только от величины скорости
Действие внешних полей на электронный газ определим через силу Лоренца
F = −e (E + v H 
c),
где v – скорость электрона, а c – скорость света. Пространственные производные от функции распределения связаны с градиентом физических величин. Здесь мы ограничимся зависимостью температуры от координат внутри газа ∂f ∂r = (∂f ∂T ) rT , а внешнее поле считаем однородным.
В этих условиях искомое отклонение можно выразить следующим образом
|
|
|
|
|
|
∂f |
|
|
|
|
|
e |
|
|
|
∂f |
|
|
|
|
e |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(v |
rT )+ |
|
|
|
|
|
|
|
|
|
|
∂f |
|
|
vη = −τ |
|
|
|
|
|
|
τ E |
|
+ |
|
|
|
|
|
|
τ |
v H |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂T |
|
|
|
|
m |
|
|
|
|
|
mc |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂v |
|
|
|
|
|
∂v |
|
|
Использование (6.27) в производных правой части равенства дает |
|
|
|
|
∂f0 |
|
|
|
|
|
|
|
|
|
|
∂f0 |
|
|
|
|
|
|
eτ |
|
|
|
∂f0 |
|
|
|
vη = −τv T |
|
+ ∂(vη) |
+eτ E |
+ ∂(vη) |
+ |
vH |
|
+ |
∂(vη) . |
|
|
|
|
|
|
|
r |
|
∂T |
|
|
∂T |
|
m |
|
|
|
∂v |
∂v |
|
|
|
|
|
|
|
|
|
|
|
∂v |
∂v |
|
|
|
|
|
|
|
mc |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(6.28а) |
|
При малых отклонениях ( f − f0 ), считая, что |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂(vη) |
<< |
∂f0 |
|
|
, ∂(vη) |
<< |
|
∂f0 |
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂T |
|
∂T |
|
|
∂v |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂v |
|
|
|
|
|
|
|
|
|
|
|
|
|
производными ∂(vη)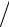
∂T и ∂(vη)
∂v в слагаемых, пропорциональных градиенту температуры rT и напряженности E можно пренебречь. В
слагаемом, отвечающем за вклад магнитного поля, производную ∂(vη)
∂v
следует сохранить. Действительно, если учесть, что ∂f0 ∂v = mv ∂f0 ∂ε, то первый член в последнем слагаемом исчезает, так как
268
v H ∂∂fv0 = v H mv ∂∂fε0 = 0 ,
и равенство (6.28а) принимает вид
|
|
∂f |
|
eτ |
∂f |
|
|
eτ |
|
|
∂(vη) |
|
f − f0 |
≡ vη = −τ(v rT ) |
0 |
+ |
|
0 |
|
+ |
|
|
|
|
|
. (6.28б) |
|
|
|
|
∂T |
E |
∂v |
|
|
v H |
∂v |
|
|
|
|
m |
|
|
mc |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Очевидно, что при наличии магнитного поля замена производных от неравновесной функции распределения, производными отфункцииравновесного распределениядала бынулевойрезультатприоценкевсехмагнитныхэффектов.
Представленное формальное решение кинетического уравнения позволяет найти потоки физических величин, в частности, плотности тока
j = −e∫ v f0d3v −e∫ v(ηv)d3v .
Поскольку равновесная функция f0 – четная по отношении к вектору скорости (6.25), а пределы интеграла симметричны, первый интеграл равен нулю. Таким образом, используя значение ηv из (6.28б), можно определить
потоки различных физических величин, в том числе, плотности потока
зарядов (плотности тока j ) и потока тепла q : |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
∂f |
|
3 e |
|
|
∂f |
|
|
|
|
|
|
|
|
|
|
|
v H |
∂f |
3 |
j =e |
∫ |
τv |
|
|
|
|
|
∫ |
|
|
− |
|
|
|
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
(v T )d v − |
|
|
|
τv E |
|
|
|
d v , (6.29) |
|
|
|
∂T |
|
|
m |
|
|
∂v |
|
|
c |
∂v |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m |
|
2 ∂f |
3 |
e |
|
2 |
|
∂f |
|
|
|
|
q = − |
|
∫ τvv |
|
|
(v rT)d v + |
|
∫ τvv |
|
E |
|
2 |
|
∂T |
2 |
|
∂v |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
v H |
∂f |
3 |
|
|
|
|
|
+ |
|
|
d v . (2.30) |
|
|
|
|
c |
|
|
|
|
∂v |
|
|
|
|
|
|
|
|
|
|
|
Эти выражения содержат полную теорию электропроводности и теплопроводности электронного газа при указанных ранее допущениях. Видно, что все внешние воздействия вносят вклад в электрический и тепловой потоки. Электрический ток возникает как под действием напряженности поля E , так и при наличие градиента температуры, а поток тепла может существовать за счет внешней силы F даже в отсутствии
269
градиента температуры. Задача определения кинетических коэффициентов потоков сводится далее к вычислению интегралов в формулах (6.29) и (6.30).
Определим электропроводность электронного газа (металлов), в
котором магнитное поле и градиент температуры отсутствуют ( H = 0 ,
rT ), а напряженность электрического поля имеет единственную отличную от нуля компоненту в направлении оси Ox , E = (E, 0, 0). С учетом
∫ τvy |
∂f |
|
d3v = ∫ τvz |
∂f |
d3v = 0 из (6.29) следует: |
|
|
∂v |
x |
|
∂v |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e2 |
E ∫ |
|
|
|
∂f |
3 |
e2 |
∫ τ(v)vx |
∂f |
3 |
|
|
|
j = − |
|
τ v |
|
|
|
d v = − |
|
|
|
d v E = σE , (6.31) |
|
|
|
m |
|
∂v |
x |
m |
∂v |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где множитель перед вектором напряженности и есть искомая электропроводность.
|
e2 |
|
∂f |
3 |
2 |
2 ∂f |
3 |
3 e2 |
|
2 |
∂f ′ |
3 |
σ = − |
|
∫ τ(v)vx |
|
|
d v = −e |
∫ τ(v)vx |
|
d v = −2m |
|
|
∫ τ(v)v |
|
0 |
|
d v |
m |
∂v |
|
∂ε |
h |
3 |
|
∂ε |
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Здесь использовано |
|
равенство |
∫ ...vx2...dv3 = ∫ ...vy2...dv3 = ∫ ...vz2...dv3 = |
= 13 ∫ ...v2...dv3 . Переходя к сферической системе координат в пространстве скоростей в подынтегральном выражении и к интегрированию по энергии
( ε = mv2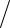
2 ), получим
|
|
|
|
|
3 ∂f0′ |
|
|
|
3/2 |
|
|
|
|
3/2 ∂f0′ |
|
σ = − |
8πm2e2 |
∫ |
τv |
dε = − |
8π 2m |
e |
2 |
∫ |
τ(ε)ε |
dε. (6.33) |
|
3 |
|
|
|
|
2 |
|
|
|
|
|
3h |
|
|
|
∂ε |
3 |
|
|
|
|
|
∂ε |
|
|
|
|
|
|
h |
|
|
|
|
|
|
|
Проводимость выражена через фермиевский интеграл, приближенное значение которого до величин второго порядка малости равно
|
|
|
∂f ′ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∞ |
|
|
|
|
|
2 |
|
|
2 |
|
|
|
|
|
∫ |
|
3/2 |
0 |
|
|
3/2 |
|
(πkT) |
|
∂ |
|
|
µ−ε |
|
3/2 |
|
, |
τε |
|
|
|
dε − τ(µ)µ |
|
+ |
|
|
|
|
|
|
|
|
τε |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂ε |
|
|
|
6 |
|
∂ε |
2 |
|
T |
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где значение второй производной по энергии берется при ε = µ. Удерживая только его первое слагаемое, из (6.33) следует
σ = 8π 2m 3/2 e2τ(µ)µ3/2 . 3 h2
Используя связь энергий Ферми с плотностью электронов
( µ0 = (h2
2m) (3n
8π)2/3 ) и пренебрегая ее зависимостью от температуры
( µ = µ0 ), для электропроводности металлов получаем
В этом выражении фигурирует время релаксации только для электронов с энергией Ферми. Следовательно, если считать τ(µ) как свободный параметр,
то нет необходимости детально изучать механизм рассеяния. В противном случае для его вычисления требуется подробная теория описывающая рассеяние. Для чистых металлов во время релаксации при высоких
температурах (T >> θD ) обратно пропорционально температуре. При плотности электронов порядка 1022 см–3 и типичной удельной проводимости для большинства металлов 105 Ом–1·см–1 из формулы (6.24) следует, что время релаксации равно примерно 10−14 с.
6.4.3. Изотермический эффект Холла. Задача вычисления кинетических коэффициентов усложняется, если газ находится не только в электрическом, но и в магнитных полях. Речь пойдет об изотермическом эффекте Холла. Считаем, что электрическое поле направлено вдоль оси Ox
E = (Ex , 0, 0), а магнитное – |
вдоль оси Oz H = (0, 0, Hz ). Если электрон |
движется в направлении x , |
то он отклоняется магнитным полем Hz в |
направлении y . Поскольку в этом направлении ток отсутствует, возникает постоянное электрическое поле Ey , называется э.д.с. Холла. Коэффициент Холла есть мера величины эффекта, и он определяется формулой
