Метода термодинамика(лекции)
.pdf2.СТАТИСТИКА ИДЕАЛЬНОГО ГАЗА
2.1.Идеальный газ как модель статистической системы
Вгазообразном состоянии плотность вещества мала, так что среднее расстояние между молекулами значительно превышают их размеры. Поэтому большую часть всего времени движения каждая из частиц (атом или молекула) находится сравнительно далеко от остальных, и силы межмолекулярного взаимодействия существенно ослаблены. Поэтому газовые молекулы движутся прямолинейно и равномерно до тех пор, пока не произойдет столкновение между данной и какой-либо другой молекулой или со стенкой сосуда. При столкновениях можно считать молекулы недеформируемыми, т.е. рассматривать их как обычные упругие шары. В процессе столкновения происходит обмен кинетической энергией между молекулами и изменение направления их полета. Зеркальное (упругое) отражение имеет место при столкновении газовой молекулы со стенкой сосуда (молекулой вещества этой стенки).
Всамом акте столкновения молекулы взаимодействуют между собой очень сильно. Их скорости могут существенно измениться как по
абсолютной |
величине, |
так и |
по |
направлению. Однако |
длительность |
(~ 10−13 сек) |
и частота |
(~ 108 |
сек-1) |
процессов соударения |
таковы, что |
подавляющую часть времени газовые молекулы движутся как свободные. Траекторию каждой из них можно представить как совокупность прямолинейных путей, образующих ломанные линии. Длина прямолинейных участков (~ 10−5 см) намного превосходит размеры молекул (~ 10−8 см). В качестве модели разреженного газа рассматривается идеальный газ.
Статистическую систему, частицы которой взаимодействуют только в процессе столкновений, а остальное время двигаются как свободные,
62
называют идеальным газом. Состояние такого газа описывает основное кинетическое уравнение состояния – уравнение Клайперона-Менделеева
|
pV = νRT , |
(2.1.а) |
где p – |
давление, V – объем, T |
– абсолютная температура, |
ν = M / m0 |
– количество молей, M – масса газа, m0 – масса моля, R – |
|
универсальная газовая постоянная. Уравнение обобщает многочисленные опытные данные и построено на идеализированной модели молекулярного движения в газе. В ее основе – пренебрежение силами сцепления (отсутствие взаимодействия). Это предположение – в столь жесткой формулировке не имеет достаточного основания. Для самопроизвольного расширения газа достаточно, чтобы средняя кинетическая энергия была больше энергии притяжения молекул при среднем их удалении друг от друга. Ведь именно благодаря энергии межмолекулярного взаимодействия совершается переход газа в конденсированное состояние вещества, жидкое или твердое. Указанный закон выполняется для большинства газов лишь приближенно и только при достаточно высокой температуре. Например, учет конечных размеров молекул и слабого молекулярного взаимодействия приводит к ряду полуэмпирических уравнений, одним из которых есть уравнение Ван-дер- Ваальса (для произвольного количества молей вещества):
( |
p +aν2 V 2 |
)( |
) |
= νRT . |
(2.1.б) |
|
V −νb |
|
Здесь притяжение молекул учитывается фактором a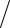
V 2 , где a – поправка на
давление, а отталкивание – «мертвый» объемом b , который приблизительно в 4 раза превышает собственный объем молекулы.
Модель точечных невзаимодействующих масс тем и удобна, что позволяет построить математическую теорию и дать физическое обоснование о самых важных явлениях молекулярного движения в газе, выяснить сложные различия между идеальным газом молекул и таким же газом электронов, фотонов и фононов, о которых речь впереди. Последовательно отказываясь от
63
различных упрощений идеальной модели, мы будем приходить к новым эффектам и явлениям. В частности, с конечными размерами молекул связаны явления переноса, с их способностью разрушаться – химические реакции, ионизироваться – электропроводности и т.д.
Газ из огромного числа молекул представляет собой механическую систему с весьма большим числом степеней свободы. Зная идеальные условия, можно было бы в принципе проинтегрировать уравнения движения всех молекул и найти их траектории. Подобное решение не представляло бы никакого интереса: свойства газа совершенно не зависят от начальных положений и скоростей молекул, т.е. не зависят от его предыстории. Газ является системой, качественно отличной от отдельной молекулы, и его поведение подчиняется иным статистическим закономерностям. Движение отдельной частицы, ее траектория и последовательность изменения состояний становится несущественной, второстепенной деталью явления.
Для выявления статистических закономерностей в соответствии с прямыми данными опыта будем использовать предположение о молекулярном хаосе, а именно: о равномерном распределении молекул в пространстве и о равномерном распределении их скоростей по всем направлениям. Столкновительные процессы не только устанавливают молекулярный хаос, но и изменяют абсолютное значение скорости молекул. Часть молекул получает избыточную кинетическую энергию за счет других молекул, соответственно потерявших часть энергии. Благодаря этому в газе возникает некоторое распределения молекул по скоростям. Если газ представлен самому себе, то числа молекул, приобретающих и теряющих скорость при столкновениях, уравниваются – устанавливается стационарное распределение по скоростям. Задача статистической физики – нахождение распределения молекул идеального газа по скоростям (энергиям), а, следовательно, определение среднего числа молекул, имеющих данные значение скорости.
64
2.2. Распределение Максвелла
Отдельно выделенная молекула идеального газа в данный момент времени находится в каком-то состоянии, которое характеризуется ее положением в пространстве, импульсом (скоростью, энергией). Через весьма короткое время в результате взаимодействия с другими молекулами она перейдет в другое состояние. Поэтому состояние одной молекулы из большой их совокупности не характеризует состояние всего газа. По этой же причине нет необходимости следить за последовательным изменением состояния отдельной молекулы с течением времени.
Задача сводится к нахождению вероятности wj того, что одна
произвольно выделенная молекула из их совокупности в равновесном идеальном газе попадает в некоторое j -е состояние. Исходя из определения
идеального газа мы имеем: 1) наличие макроскопической системы (термостата) – газа, окружающего молекулу (подсистему); 2) слабое взаимодействие между молекулой и термостатом. Эти условия характеризуют ансамбль, подчиняющийся каноническому распределению Гиббса.
G G
Элемент фазового объема в µ–пространстве (шестимерном) dΓ = dqdp
в декартовой и сферической системах координат соответственно равен dΓ(pG,rG) = dpxdpydpzdV , dΓ(p, θ,ϕ,rG) = p2 sin θdpdθdϕdV ,
а кинетическая энергия молекулы (в отсутствии внешнего поля) есть
ε = (p2 |
+ p2 |
+ p2 ) 2m = p2 |
2m = m(v2 |
+v2 |
+v2 ) 2 = mv2 |
2. (2.2) |
x |
y |
z |
x |
y |
z |
|
Подстановка этих выражений в распределение Гиббса определяет вероятность для молекулы находится в объеме dV и иметь энергию (импульс) в интервале от ε(p) до ε +dε ( pG +dpG):
65
G G |
e−ε/θdΓ |
|
dV |
3 |
e−p2j /2mθdpj |
|
|
|||
dw(q, p) = |
|
|
= |
|
∏ |
|
|
|
, |
(2.3) |
∫e |
−ε/θ |
V |
∫ e |
−p2 |
/2mθ |
|||||
|
dΓ |
|
j=1 |
j |
dpj |
|
|
|||
(pj )
где j = x, y, z . Представление искомой вероятности в виде произведения
сомножителей dV /V и ∏(...) свидетельствует о независимости импульса
j
(скорости) молекулы от ее положения в пространстве и о независимости проекций импульса (скоростей).
В кинетической теории газа принято считать, что проекции импульса (скорости) могут принимать значения от −∞ до +∞. В этом приближении интегралы в знаменателе (2.3) оказываются равными
+∞ |
+∞ |
∫ e−p2j /2mθdpj = (2πmθ)1/2 , |
∫ e−mv2j /2θdpj = (2πθ m)1/2 . |
−∞ |
−∞ |
Подстановка их в исходное равенство позволяет найти вероятности того, что молекула имеет как проекции, так и абсолютное значение скорости,
импульса (dw(vx ), dw(px ),dw(v), dw(p)) и кинетическую энергию dw(ε) :
|
dw(vx ) = (m 2πkT )1/2 e−mvx2 |
2kTdvx ; |
(2.4) |
||||||||
|
dw(px ) = (2πkT)− 1/2 e− px2 |
2mkTdpx ; |
|||||||||
|
|
||||||||||
dw(vG) = (m 2πkT )3/2 e−mv2 |
2kT v2 dv sin θdθdϕ, |
(2.5) |
|||||||||
G |
( |
) |
− 3/2 |
|
−p2 2mkT |
|
|
|
|
||
e |
p |
2 |
dp sin θdθdϕ; |
|
|||||||
dw( p ) = 2πmkT |
|
|
|
|
|
|
|||||
dw(v) = 4π(m 2πkT )3/2 e− mv2 |
2kT v2 dv ; |
(2.6) |
|||||||||
|
dw( ε) = 2π(πkT )− 3/2 e− ε kT |
εd ε. |
(2.7) |
||||||||
Формулы получили название распределение Максвелла. Здесь модуль статистической температуры заменен на θ = kT . Правомерность замены обоснована в следующем разделе. Знание указанных вероятностей дает
66
возможность определить плотность числа молекул, обладающих соответствующими параметром:
dn(x) = ndw(x) , |
(2.8) |
|||
где n – общая плотность молекул, x = |
{ |
v |
, p , v, |
p, ε... . |
|
x |
x |
} |
|
2.3. Столкновения молекул со стенкой сосуда. Давление
При движении в замкнутом сосуде молекула газа, приближаясь к стенке, со стороны ее молекул испытывает весьма сильное отталкивание и отражается внутрь сосуда. Можно считать, что отражение молекулы от стенки сосуда происходит совершенно упруго, т.е. компонента скорости, перпендикулярная плоскости стенки, при отражении меняет знак.
Выделим в стенке сосуда площадью dS , перпендикулярную оси Ox . Тогда при отражении от нее молекула, имевшая компоненты скорости vx , vy, vz , приобретает компоненты скорости – vx , vy, vz , т.е. происходит
изменение проекции импульса на оси Ox от значения mvx до значения
−mvx . Это изменение импульса 2mvx передается отражающей стенке. Таким образом, столкновения молекул со стенкой приводит к появлению силы, действующей на поверхность сосуда. Силу, действующую на единицу поверхности стенки со стороны всех молекул газа, отождествляют с макроскопическим давлением. Такое утверждение, являющееся по сути основой кинетической теории газов, казалось в свое время радикальным. Однако сейчас оно представляется естественным и очевидным.
Для определения давления нужно вычислить полное изменение количества движения молекул газа, испытывающих отражение от единицы поверхности сосуда в единицу времени. Очевидно, оно равно изменению импульса в одном соударении со стенкой (2mvx ), умноженному на полное число ударов в 1 сек на 1 см2 поверхности. В единицу времени поверхности
67
стенки будут достигать все молекулы, находящиеся от нее на расстоянии,
меньшем или равным |
v |
x |
. На 1 см2 поверхности за 1 сек попадают все |
||||
|
|
|
|
|
|
|
|
молекулы, находящиеся в цилиндре высотой v |
x |
с основанием 1 см2 |
(Рис. 2.1). |
||||
|
|
|
|
|
|
|
|
В его объеме vx |
(см3) |
находится vxdn(vG) молекул, компонента скорости |
|||||
которых лежат |
между |
|
|
vx и vx +dvx ; vy |
|
и vy +dvy ; vz и |
vz +dvz . |
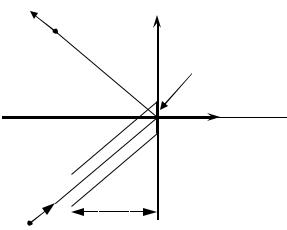
Поверхности стенок достигают все молекулы, находящиеся в указанном цилиндре, независимо от значения компонент скорости vy и vz . Здесь не
учитываются столкновения молекул между собой. Однако, молекулы, не достигающие стенки из-за соударений, передают свой импульс молекулам, долетающим до стенки.
|
|
|
|
y |
|
(−vx ,vy ,vz ) |
|
∆S =1 |
|
|
x
(vx ,vy ,vz ) |
|
|
|
|
|
||
|
|
vx |
|
|
|
||
|
|
|
|
||||
|
|||||||
|
|
|
|
|
|
|
|
|
Рис. 2.1. |
||||||
Число молекул с проекцией скорости vx , которые за 1 сек достигают поверхности стенки и общий импульс, передаваемый ими, равны
|
|
|
|
|
|
m |
1/2 |
|
−mvx2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2θ |
|
|
|
. |
|
dν(v |
) = v |
dn(v |
) = v |
ndw(v |
) = n |
|
|
e |
|
|
v |
dv |
x |
|
|
|
|
||||||||||||
x |
x |
x |
x |
x |
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
2πθ |
|
|
|
|
|
|
|
|
dp(vx ) = 2mvxdν(vx ).
Для вычисления полного импульса проинтегрируем последнее выражение по всем возможным значениям компоненты скорости vx от 0 до ∞:
68
|
∞ |
|
|
|
1/2 |
∞ |
|
−mvx2 |
|
|
|
|
|
|
|
|
∫ |
|
|
m |
∫ |
|
|
|
2 |
|
|
N |
θ. |
||
|
|
|
|
2θ |
|
|
|||||||||
p = |
dp(v |
) = 2nm |
|
|
e |
|
|
v |
dv |
|
= nθ = |
|
|||
|
|
|
|
|
|||||||||||
|
x |
|
|
|
|
|
|
x |
|
x |
|
V |
|
||
|
0 |
|
|
2πθ |
0 |
|
|
|
|
|
|
|
|
||
Отрицательные проекции скорости в расчет не берутся, т.к. эти молекулы движутся в противоположном направлении и не передают своего импульса стенке. Вычисленная таким образом величина есть сила, действующая на единицу площади, т.е. давление.
Сопоставление (2.9) с уравнением состояния одного моля ( ν = 1) разреженного газа (2.1.а), полученным опытным путем, определяет модуль статистического распределения Гиббса через абсолютную температуру
θ = kT . |
(2.10) |
2.4. Характерные величины идеального газа
2.4.1.Свойства распределения Максвелла . На рис. 2.2 и
2.3изображена функция распределения по проекциям и абсолютной
величине скорости (2.4), (2.6). По оси ординат отложены значения dw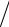(x1)
dx1
и dw(x2 )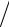
dx2 , а по оси абсцисс – величины x1 = (m
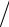2kT )1/2 vx и
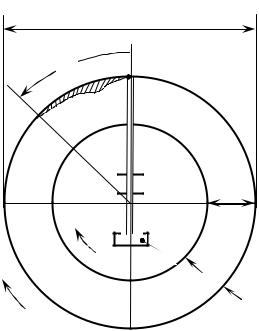
x2 = (m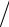
2kT )1/2 v , соответственно. В первом случае (рис. 2.2) кривая
x |
= |
m |
v |
|
|
2kT |
x |
||||
1 |
|
|
|||
|
|
|
|
|
x2 = |
m |
v |
|
2kT |
|||
|
|
||
|
|
|
Рис. 2.2. |
Рис. 2.3. |
69
распределения симметрична по отношению к положительным и отрицательным значениям vx , имеет максимум при vx = 0 и асимптотически обращается в нуль при стремлении аргумента к бесконечности. Кривая распределения по абсолютным значениям скоростей (рис. 2.3) обращается в нуль при v = 0 , проходит через максимум и асимптотически стремится к нулю при бесконечно больших значениях скоростей. Таким образом, число молекул в газе с очень малыми и очень большими абсолютным скоростями оказывается сравнительно небольшим. Формулы позволяют найти число очень быстрых и очень медленных молекул. С ростом температуры распределение становится более пологим: относительное число молекул с большими значениями скоростей возрастает.
2.4.2. Опыт Штерна . Распределение Максвелла суть – частный случай канонического распределения Гиббса, которое получено из теоретической модели, исходя из общих физических предположений. Непосредственная его проверка невозможна. Поэтому экспериментальная проверка распределения Максвелла имеет принципиальное значение – является одной из важнейших задач молекулярной физики. Существуют разные методы измерения распределения молекул по скоростям; здесь рассмотрим опыт Штерна.
Модель его установки показана на рис. 2.4. В качестве объекта исследования используют пары металлов (висмут, кадмий, цезий и др.), которые испаряются из плавильной печи (1) в вакуум. Через систему щелей
(s1 , s2 ) из них формируется узкий молекулярный пучок (выделяются молекулы имеющие одну компоненту скорости, например, vx ). На пути пучка устанавливаются два синхронно вращающихся цилиндра (2) и (3), радиусы которых отличаются на величину l , а внутренний имеет небольщую прорезь. Пучок достигает поверхности внешнего цилиндра (3), если щель во внутреннем цилиндре находится против щелей в экранах s1 и s2 . При
70
2R |
|
|
бесконечной |
скорости |
(vx ∞) |
||||
z |
A |
|
|
молекулы |
оседали бы в точке |
A, |
|||
|
|
находящейся |
|
против |
щели |
||||
|
|
|
|
|
|||||
|
|
|
|
внутреннего цилиндра. Но поскольку |
|||||
|
|
|
|
молекулы имеют разные скорости, то |
|||||
|
s2 |
l |
|
они оседают |
в |
точке z , расстояние |
|||
|
s1 |
|
которой от точки A зависит от их |
||||||
|
|
|
|
||||||
|
1 |
|
|
скорости. |
Оно |
увеличивается |
с |
||
|
|
|
уменьшением |
|
скорости. |
При |
|||
|
2 |
|
|
|
|||||
|
|
|
3 |
заданной угловой скорости вращения |
|||||
|
|
|
|
цилиндров ω частицы, летящие по |
|||||
Рис. 2.4. |
|
|
инерции |
в |
пространстве |
между |
|||
|
|
цилиндрами, оседают на расстоянии |
|||||||
|
|
|
|
||||||
z =ωR t =ωRl / vx |
от точки |
A. В процессе эксперимента на внутренней |
|||||||
поверхности внешнего цилиндра (охлаждается жидким воздухом!) |
|||||||||
образуется слой из осевших молекул, толщина которого отражает обратное |
|||||||||
распределение Максвелла. Измеренная фотометрическим методом толщина |
|||||||||
слоя как функция смещения |
z |
подтвердила распределение Максвелла по |
|||||||
скоростям. |
|
|
|
|
|
|
|
|
|
В отличие от распределения Гиббса распределение Максвелла |
|||||||||
изображается размытой кривой. Это обусловлено тем, что в моделях |
|||||||||
рассматривались разные системы. Распределения Гиббса относится к |
|||||||||
системам с очень большим числом частиц (ширина размытости обратно |
|||||||||
пропорциональна их числу), а распределение Максвелла – к системам с одной |
|||||||||
частицей. |
|
|
|
|
|
|
|
|
|
2.4.3. Средние скорости и энергия молекул . Из |
|||||||||
распределения Максвелла можно найти средние значения любых величин, |
|||||||||
71