
Метода термодинамика(лекции)
.pdfНапример, для равновесного идеального газа, используя его функцию состояний (2.42) и следуя указанному ранее алгоритму, определим его внутреннюю E и свободную F энергии, теплоемкость CV , химический потенциал µ, уравнение состояния и энтропию S :
E = |
3 |
|
|
|
|
|
|
eV |
2πmkT 3/2 |
|
|
C = |
3 |
Nk |
; |
|
|||||||||
|
NkT ; F = −NkT |
|
|
|
|
|
|
|
; |
|
|
||||||||||||||
|
|
2 |
|
|
|
|
|
|
|
|
|
|
h |
2 |
|
|
|
|
V |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
N |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂F |
|
|
|
|
|
|
|
1 |
3/2 |
|
|
|
NkT |
|
|
νRT |
|
|||||||
|
|
N |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
µ = |
|
|
|
|
= kT ln |
|
|
|
|
|
|
|
|
; |
p = |
|
|
|
= |
|
|
; |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
∂N |
|
|
|
V |
|
2πmkT |
|
|
|
|
|
|
|
|
V |
|
|
V |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
T,V |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
∂F |
= Nk ln |
V |
+N |
|
3 |
k ln kT + |
5 |
|
|
|
|
|
(3.68) |
|||||||
S = − |
|
|
|
|
|
k +kj . |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
N |
|
|
|
2 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
∂T V |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Рассмотрим |
|
вопрос |
о изотермическом |
|
смешивании |
|
разных газов с |
||||||||||||||||||
массами атомов m1 и m2 , которые в исходном состоянии характеризовались объемами V1 и V2 и числом частиц N1 и N2 . В процессе смешивания молекулы обоих порций газа начинают диффундировать, заполняя весь объем V =V1 +V2 . Вычислим изменение энтропии при таком процессе. В
начальный момент энтропии обоих порций газа были равны (3.68)
S 0 |
= kN |
|
ln |
Vj |
+N |
f(T |
,m |
), j = 1,2 |
j |
|
|||||||
j |
|
|
Nj |
j |
j |
j |
|
|
|
|
|
|
|
|
|
|
После смешивания каждый газ ведёт себя автономно, и энтропия изменяется в связи с увеличением объема:
S 0 |
= kN |
j |
ln V |
+N |
f(T |
,m |
), j = 1,2 |
j |
|
Nj |
j |
j |
j |
|
|
|
|
|
|
|
|
|
Суммарное изменение энтропии при таком процесс определяется выражением
∆S = (S |
+S |
) −(S 0 |
+S 0 ) = kN |
ln V |
+kN |
ln V |
= |
||||||
|
1 |
2 |
|
1 |
|
2 |
1 |
|
V |
1 |
V |
|
|
|
|
N1 +N2 |
|
|
|
N1 +N2 |
1 |
|
2 |
|
|||
= kN |
ln |
+kN |
ln |
> 0. |
|
|
|||||||
|
|
|
|
||||||||||
1 |
|
|
N1 |
|
|
1 |
|
N2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
152
Таким образом, энтропия после смешивания увеличивается, процесс необратимый. Это понятно, так как для обратного разделения газов требуется затратить некоторую работу. Другой характер имеет процесс смешивания одинаковых газов, когда функция f (T,m1) = f (T,m2 ) = f (T,m) . Проведя аналогичные предыдущим рассуждения, легко доказать, что
∆S = kN |
ln |
V1 +V2 |
|
N1 |
+kN |
ln ln |
V1 +V2 |
|
N2 |
= 0 , |
|
|
|
|
|||||||
1 |
|
N1 +N2 V1 |
1 |
|
N1 +N2 V2 |
|
||||
|
|
|
|
|
||||||
ив этом случае процесс обратимый.
3.8.Третье начало термодинамики (теорема Нернста)
В 1906 г. на основе большого числа исследований многообразных свойств при температурах, близких к абсолютному нулю, В.Ф.Г. Нернстом был установлен новый закон – третье начало термодинамики. Согласно этому закону в авторской формулировке, изменение энтропии во всех процессах при абсолютном нуле равно нулю. Иными словами энтропия есть абсолютная постоянная, не зависящая ни от объема, ни от давления. Более узкой была формулировка М. Планка: энтропия идеально образованных кристаллов при абсолютном нуле равна нулю.
Этот закон особенно нуждается в статистическом обосновании, так как он, во-первых, не подкреплен таким богатым экспериментальным материалом, как первое и второе начала, а во-вторых, существуют системы, свойства которых не удовлетворяют третьему началу. Рассмотрим произвольную макроскопическую систему в состоянии статистического равновесия с энергией ε при весьма низких температурах. Пусть её возможные энергетические уровни образуют последовательность ε0 , ε1 , ε2 , …, где ε0 –
наименьшая возможная энергия (нормальный уровень), а ε1 , ε2 , ... –
возбужденные энергетические уровни. Считаем, что система удовлетворяет
153

каноническому распределению Гиббса (1.59), и запишем её функцию состояния при заданных T , V и N (1.60):
|
− |
ε0 |
|
− |
∆ε1 |
|
− |
∆ε2 |
|
Z = e |
|
|
|
|
|
+Ω(ε2 )e |
|
|
+... |
|
|
Ω(ε0 ) +Ω(ε1)e |
|
kT |
|
kT |
|||
|
|
kT |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где ∆εj = εj −ε0 . Уровни энергии быстро сближаются с ростом возбуждения так, что уже при малых энергиях возбуждения расстояние между уровнями ничтожно мало. Если температура системы очень низка, а именно: kT << ∆ε1 ,
то тепловые возбуждения недостаточны для того, чтобы система могла попасть в состояние ε1 , она должна находится в состоянии с наименьшей энергией ε0 .
Эти условия определяют функцию состояний и свободную энергию
− ε0
Z e kT Ω(ε0 ) ; F = kT ln Z = ε0 −kT ln Ω(ε0 ).
Здесь ε0 не зависит от температуры и является внутренней энергией равновесной системы E = ε0 . Отсюда находим энтропию
S = − ∂F = k ln Ω(E)∂T V
T <<∆ε1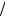 T
T
Поскольку энергия системы точно определена, то тем самым заданы состояние системы и кратность вырождения. Поэтому энтропия при стремлении температуры системы к нулю является постоянной величиной:
= const . (3.69.а)
Это и есть содержание третьего начала термодинамики. Если кратность вырождения нормального уровня равна единице Ω(ε0 ) = 1, то приходим к формулировке Планка
= 0 (3.69.б)
Теорема Нернста является следствием квантовой статистики, где существенное значение имеет дискретность состояний. Энергия невырожденной системы меняется непрерывным образом, и даже в весьма
154

малом интервале энергий ∆ε ~ kT существует изменяющееся бесконечно большое число возможных состояний Ω. Поэтому энтропия не может быть постоянной при любой как угодно низкой (но конечной) температуре. Однако при температуре, близкой к абсолютному нулю, практически все системы становятся вырожденными. По этой причине третье начало термодинамики рассматривается как общий закон для любых равновесных систем безотносительно к их агрегатному состоянию. Формула (3.69) справедлива в равной мере для твердых, жидких или газообразных веществ.
В жидкой фазе вблизи абсолютного нуля существует только гелий II. Все обычные газы при достаточном давлении конденсируются задолго до тех температур, при которых энтропия стремится к нулю. Существуют, однако, системы, которые можно условно считать газообразными при T → 0, это прежде всего электронный газ в металле. Все же обычные вещества при достаточно низкой температуре переходят в твердое состояние.
Из теоремы Нернста следует, что любые |
теплоемкости системы |
|
(~ ∂S ∂T ), коэффициент объемного расширения (~ (∂V ∂T) |
= −(∂S ∂p) ), |
|
|
p |
T |
термический коэффициент давления (~ (∂p ∂T) = |
(∂S ∂V ) |
) обращаются в |
V |
T |
|
нуль. |
|
|
Часто третье начало термодинамики формулируют как недостижимость |
||
абсолютного нуля. Представим себе цикл Карно, у которого холодильник имеет температуруT1 = 0 °К, и тогда, согласно (3.69), ∆S1 = 0 . Для такой обратимой машины полное изменение энтропии в цикле равнялось бы её изменению на участке изотермического (T =T2 ) подвода тепла (первый этап)
∆S = ∆S2 |
= |
∆Q2 |
|
T2 |
|||
|
|
Но, с другой стороны, в связи с обратимостью процесса суммарное изменение
∆S = 0 . Возникшее противоречие (∆Q2 ≠ 0 ) доказывает недостижимость нулевой изотермы T1 = 0 °К. Данное положение, конечно, не запрещает
155
приближаться к T = 0 °К сколь угодно близко. Следствия из теоремы Нернста относятся к непосредственно измеряемым величинам. Действительно, для ряда веществ при T → 0 (алмаз, HCl , Cu и др.) экспериментальные результаты полностью подтвердили выводы теории. Однако, для большей части тел энтропия оказывается не равной нулю (или константе) при очень низких температурах. К ним относятся аморфные тела, сплавы, а также ряд химических соединений: CO , NO , и H2O т.д. Объясняется это тем, что подобные системы при весьма низких температурах не являются равновесными. Из-за малости тепловой энергии возбуждения (большого времени релаксации) в них происходит очень длительный процесс, приближающий их к состоянию равновесия (метастабильное состояние).
3.9. Применения термодинамики
3.9.1. Охлаждение газа при необратимом адиабатическом расширении . Рассмотрим задачу получения низких температур путем сжижения газов. Для её решения необходимо уменьшить скорость теплового движения молекул газа и сблизить их. Последнее достигается сжатием газа с помощью компрессоров, а для понижения температуры газ заставляют совершать работу при адиабатическом расширении. Процесс может происходить как необратимо, так и обратимо. Здесь мы ограничимся анализом обратимого процесса расширения газов.
Вильям Томсон (лорд Кельвин) предложил и осуществил совместно с В. Джоулем следующий опыт. Была взята теплонепроницаемая (∆Q = 0 )
трубка, сделанная из самшита, с двумя скользящими поршнями и пробкой из прессованной ваты (рис. 3.3). Перемещая поршни, можно осуществить стационарное протекание газа сквозь пробку так, чтобы слева существовало постоянное давление p1 , а справа – p2 . Опыт заключается в измерении малого изменения температуры газа при продавливании его сквозь пробку.
156

|
V1, |
p |
p1 |
1 |
|
V2, |
|
p2 |
p |
|
2 |
Рис. 3.3.
Из-за трения в перегородке скорость течения газа мала, и поток не является турбулентным, то есть газ по обе стороны перегородки однороден. Кинетическая энергия газа и потери на трение в пористой перегородке при малой скорости пренебрежимо малы (~ квадрату скорости). Работа,
совершаемая над газом при продавливании сквозь пробку его объема V1 при
давлении |
|
p , равна |
|
pV . Справа от перегородки газ совершает работу при |
||||||||||||
|
|
1 |
|
|
|
1 |
1 |
|
|
|
|
|
|
|
|
|
давлении |
|
p2 , расширяясь до объема V2 . Общее изменение работы во всей |
||||||||||||||
системе |
равно pV − pV . |
Поскольку |
процесс |
адиабатический (система |
||||||||||||
|
|
|
|
1 |
1 |
|
2 |
2 |
|
|
|
|
|
|
|
|
теплоизолирована, |
|
∆Q = 0 ), |
то |
из |
первого |
начала термодинамики |
||||||||||
(∆E = E |
2 |
−E |
1 |
= −pV + pV ) имеем |
|
|
|
|
||||||||
|
|
|
|
2 |
2 |
|
1 |
1 |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
E |
2 |
+ pV = E |
1 |
+ pV = const , |
|||||
|
|
|
|
|
|
|
|
|
2 |
2 |
|
1 |
1 |
|
||
то есть процесс Джоуля-Томсона является изоэнтальпическим, проходит при
постоянной энтальпии H1 = H2 . Это дает нам возможность определить изменение температуры газа при его расширении с перепадом давления
∆p = p2 − p1 < 0 . Процесс при небольших перепадах давления ∆p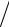 p1 << 1
p1 << 1
носит название дифференциальный эффект Джоуля-Томсона. В этом случае ∆p
и ∆T малы, иприращение ∆H(p,T) можнопредставитьследующимобразом
|
|
|
|
|
|
|
|
∆H = |
|
∂H |
|
|
∂H |
∆p |
|
|
|
|
∆T + |
|
|||
|
|
|
|
|
|
|
|
|
|
∂T p |
|
|
∂p T |
|
|
Из равенства ∆H = 0 находим |
|
|
|
|
|
|
|
χ = |
∆T |
= − |
(∂H ∂p) |
. |
|||
|
T |
||||||
∆p |
(∂H ∂T ) |
||||||
|
|
|
|
|
|
p |
|
|
|
|
|
157 |
|
|
|

С другой стороны, из выражения для дифференциала энтальпии
|
|
|
|
|
|
∂H |
|
∂S |
+V , и |
(dH =TdS +Vdp ) следует, что |
|
=T |
|
|
|
|
|
|
|
|
∂p T |
|
∂p T |
|
|
T (∂S ∂p) |
|
+V |
T (−∂V ∂T ) |
+V |
. |
||||
χ = − |
|
T |
= − |
|
|
T |
||||
|
Cp |
|
|
|
|
Cp |
|
|||
|
|
|
|
|
|
|
|
|
||
Таким образом, коэффициент Джоуля –Томсона оказывается равным |
||||||||||
|
|
χ = |
T (∂V ∂T ) |
−V |
. |
|
(3.70) |
|||
|
|
|
|
|
T |
|
||||
|
|
|
|
Cp |
|
|
||||
|
|
|
|
|
|
|
|
|
||
Входящая в формулу производная находится из уравнения состояния. Так, для идеальных газов ( pV = NkT ) χ = 0 . Объясняется это положение тем,
что эффект Джоуля-Томсона отражает влияние сил взаимодействия между молекулами газа, а эти силы у идеальных газов не учитываются.
Иная картина наблюдается для газа Ван-дер-Ваальса:
(p +a V 2 )(V +b) = NkT .
V 2 )(V +b) = NkT .
Дифференцируя это уравнение состояния по T при постоянном давлении, получим
|
|
|
Nk(V −b) |
|
|
|
∂V |
|
. |
||
|
|
= |
|
|
|
|
|
||||
|
|
|
3 |
2 |
|
|
∂T p |
|
NkT −(2a V |
)(V −b) |
|
Считая газ не очень плотным и отбрасывая в последнем соотношении величины второго порядка малости по a и b , получим
|
|
|
|
1 V −b |
|
1 |
|
|
|
|
∂V |
|
|
|
|||||
|
|
≈ |
|
|
|
= |
|
V −b +2a NkT . |
|
|
|
|
|
||||||
|
|
|
T 1 −2a NkTV |
|
T |
|
|
||
|
∂T p |
|
|
|
|
||||
|
T (∂V ∂T )T |
−V |
V −b +2a NkT −V |
2a NkT −b |
|||||
χ = |
|
|
|
= |
|
|
= |
|
. (3.71) |
|
|
|
|
|
|||||
|
|
Cp |
|
|
|
Cp |
Cp |
||
Отсюда следует, что
158

а) изменение температуры не очень плотного газа при адиабатическом |
||||||||||||
расширении зависит от соотношения величин a и b , |
которые оказывают |
|||||||||||
противоположное влияние на знак эффекта; |
|
|
|
|
|
|||||||
б) если силы взаимодействия между молекулами велики, так что |
||||||||||||
преобладает |
поправка |
на |
давление (2a NkT >>b ), |
то |
χ > 0 |
– |
газ |
|||||
охлаждается (∆T < 0 , |
так как ∆p < 0 ). (Положительный эффект Джоуля- |
|||||||||||
Томсона). |
|
|
|
|
|
|
|
|
|
|
|
|
в) если силы взаимодействия между молекулами малы (a → 0), то |
||||||||||||
наблюдается |
отрицательный |
эффект |
Джоуля-Томсона, |
χ < 0 , |
газ |
|||||||
нагревается. |
|
|
|
|
|
|
|
|
|
|
|
|
В первом случае (b → 0 ) расширяющийся газ за весь процесс совершает |
||||||||||||
работу pV −pV > 0 |
за |
счет |
убыли |
его |
внутренней |
энергии |
– |
газ |
||||
2 |
2 |
1 |
1 |
|
|
|
|
|
|
|
|
|
охлаждается. |
Во |
втором |
случае (a → 0) |
полная |
работа над |
газом |
||||||
pV −pV > 0 идет на увеличение его внутренней энергии – газ нагревается. |
||||
1 |
1 |
2 |
2 |
|
|
|
Так как dH =Vdp +TdS = 0 , то (∂S ∂p)H |
= −V T < 0 и при ∆p < 0 |
|
имеем ∆S > 0 , то есть переход газа к меньшему давлению осуществляется путём необратимого процесса с увеличением энтропии.
3.9.2. Термодинамика диэлектриков и магнетиков . Раздел посвящен анализу свойств физических систем, на которые действуют еще и немеханические силы, связанные, например, с электрическим и/или магнитным полем. Здесь в выражения дифференциалов термодинамических потенциалов следует добавлять слагаемое, ответственное за работу указанных немеханических сил, например,
δE = −pδV +TδS + Λδλ
Вопрос о внешнем параметре (λ) и внешней обобщенной силе ( Λ) решается в каждом конкретном случае по-своему. Если речь идет о диэлектрике во внешнем электрическом поле, то напряженность последнего есть внешний
159
параметр. Удельная (на единицу объема) работа, совершаемая внешними электрическими силами, равна δAE = −PGδEG, где PG – вектор поляризации диэлектрика (дипольный момент единицы объема), δEG – изменение средней электрической напряженности. В таком представлении работа учитывает не только изменение энергии диэлектрика в результате его поляризации, но и
GG
его потенциальную энергию в электрическом поле U = (−PE) при
фиксированном PG. Тогда работа только на поляризацию будет равна
δAP = δAE −δU = EGδPG.
Таким образом, если в качестве переменной величины рассматривается вектор поляризации PG, то дифференциалы внутренней и свободной энергий определяются выражениями
dE = −pdV +TdS +EGdPG; |
(3.72) |
dF = −pdV −SdT +EGdPG. |
(3.73) |
Для расширенной системы (см. раздел 3.7, формулу (3.66), где роль независимой переменной исполняет напряженность электрического поля, дифференциалы потенциала Гиббса и энтальпии принимают вид
dΦ =Vdp −SdT −PGdEG; |
(3.74) |
dH =Vdp +TdS −PGdEG |
(3.75) |
Последние слагаемые в дифференциалах потенциалов можно представить |
|
через индукцию DG , учитывая материальное уравнение DG = EG + 4πPG :
G G |
|
|
G |
|
G |
|
|
1 G G |
|
E |
2 |
|
|
|
|
|
D |
−E |
|
|
|
|
|
|
|
||||||
EdP |
= d |
|
|
|
|
= |
|
EdD |
−d |
|
|
|
|
, |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
2 |
|||||||||
|
|
|
4π |
|
4π |
|
|
8π |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
||||||
G G DG −EG G |
|
1 G G |
E2 |
|
|||||||||||
PdE = |
|
|
|
dE = |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
DdE −d |
|
|
. |
|
|||||||
|
|
4π |
|
|
|
|
4π |
|
|
8π |
|
|
|||
|
|
|
|
|
|
|
|
|
|
||||||
Слагаемые d (E2 8π) представляют собой изменение энергии внешнего электрического поля при помещении в него диэлектрика. Предполагая
8π) представляют собой изменение энергии внешнего электрического поля при помещении в него диэлектрика. Предполагая
160

малость объема диэлектрика, этим изменением энергии можно пренебречь, что приводит к выражениям
dE = −pdV +TdS + |
EGdDG |
; |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|||||
|
|
|
|
G4πG |
|
|
|
|
|
|
||
dF = −pdV −SdT + |
EdD |
|
; |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|||||
|
|
G G4π |
|
|
|
|
|
(3.76) |
||||
dΦ =Vdp −SdT − |
DdE |
; |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|||||
|
|
G4πG |
|
|
|
|
|
|
||||
dH =Vdp +TdS − |
DdE |
. |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
||||||
|
|
4π |
G |
G |
G |
G |
G G |
|||||
|
|
|
|
|
|
|
||||||
При замене электрических величин магнитными (P |
→ M , E |
→ H |
, D → B ) |
|||||||||
в формулах (3.72)-(3.76) приходим к дифференциалам потенциалов систем в магнитном поле. В частности, для потенциала Гиббса имеем:
G G |
(3.77) |
dΦ =Vdp −SdT −MdH |
Эти выражения – основа термодинамики диэлектриков и магнетиков, они позволяют определить ряд электродинамических параметров и установить соотношения между различными свойствами.
С молекулярной точки зрения, внешнее электрическое поле изменяет значения уровней энергии системы. При бесконечно малом изменении напряженности δEG энергия i –го уровня изменится на величину
δεi = −Λiδλi = PGjδEG,
G
где Pj представляет обобщенную силу, отвечающую обобщенной координате
EG. Во внешнем поле энергия и вектор поляризации системы в j –ом состоянии приобретают значения
|
εj |
= εj (0) +∆εj (PGδEG), |
PGj = −δεj δEG = −δ(∆εj (EG)) δEG . |
||
|
|
= −PGδEG, находим среднее значение вектора |
Отсюда, учитывая δE = δεj |
||
поляризации |
|
|
161
