
Метода термодинамика(лекции)
.pdf
характеризующих свойства газовых молекул. Например, среднее значение компоненты скорости:
|
|
|
|
|
∞ |
|
|
|
m |
1/2 |
∞ |
|
−mvx2 |
|
|
|
|
|
|
|
|
|
|
∫ |
|
|
|
|
∫ |
|
|
2kT |
|
|
|
= 0 . |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
v |
|
|
= |
v |
dw(v |
) = |
|
|
e |
|
|
v |
dv |
|
||||
|
|
x |
|
x |
x |
|
|
|
|
|
|
x |
|
x |
|
|||
|
|
|
|
|
−∞ |
|
|
|
2πkT |
−∞ |
|
|
|
|
|
|
|
|
Этот результат очевиден, если учесть равновероятность движения молекул в двух противоположных направлениях. Аналогичные вычисления дают vy = vz = 0 , а следовательно, vG = 0 . Среднее значение абсолютной скорости
|
|
: |
определим, учитывая распределение (2.6) и интервал изменения v 0; |
∞ |
|
|
|
|
|
|
|
∞ |
|
|
|
|
|
3/2 ∞ |
|
|
−mv2 |
|
|
|
|
1/2 |
|
|||
|
|
|
∫ |
|
|
m |
|
|
∫ |
|
|
2kT |
3 |
2 |
|
2kT |
|
||||
|
|
|
|
|
|
||||||||||||||||
v |
= |
vdw(v) = 4π |
|
|
|
|
|
e |
|
v dv = |
|
|
|
. |
(2.11) |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m |
|
|
||||
|
|
|
0 |
|
2πkT |
|
0 |
|
|
|
|
|
π |
|
|
||||||
Из условия |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d |
|
−mv2 |
|
2 |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
2kT |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
e |
|
|
v |
|
|
= 0 |
|
|
|
|
|
|
||
|
|
|
|
|
dv |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
найдем наиболее вероятную скорость молекул газа, при которой максвелловское распределение имеет максимум:
vm = (2kT m)1/2 |
(2.12) |
В соответствии с полученными формулами средняя и наиболее вероятная скорости молекул возрастают с ростом температуры и обратно пропорционально корню квадратному из массы молекулы.
Вычисления
|
|
|
∞ |
|
|
m |
3/2 |
∞ |
|
−mv2 |
|
3 |
|
|
|
2 |
|
2 |
|
|
|
||||||||||
|
∫ |
|
|
∫ |
|
2kT 4 |
|
2kT |
|||||||
v = |
|
|
|
|
e |
|
v dv = |
|
|
|
|
||||
|
v dw(v) = 4π |
|
|
|
|
|
|
|
|
||||||
|
|
|
0 |
|
|
2πkT |
0 |
|
|
|
2 |
|
m |
|
|
определяют среднюю кинетическую энергию поступательного движения
газовой молекулы
ε = mv2 2 = 3kT 2. |
(2.13) |
72
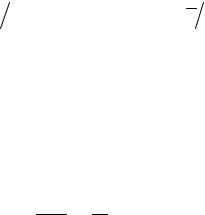
Она не зависит от природы молекулы и пропорциональна температуре газа T . Средняя (внутренняя) энергия E газа, равна сумме энергий всех его молекул:
E = N ε = |
3 NkT , |
(2.14) |
|
2 |
|
где N – полное число молекул в газе. Средняя энергия механического движения молекул газа отождествляется с макроскопической тепловой энергией. С кинетической точки зрения абсолютная температура есть величина, характеризующая среднюю энергию движения молекул.
В силу равноправия всех направлений в пространстве средняя энергия движения молекулы в каждом направлении должна быть одинаковой. Но поскольку каждая молекула имеет три степени свободы, и ее движение может быть разложена на движение в трех взаимно перпендикулярных направлениях, то из формулы (2.13) следует, что на каждую степень
свободы в среднем приходится энергия, равная kT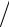 2 . Это утверждение –
2 . Это утверждение –
частный случай весьма общего закона о равномерном распределении энергии по степеням свободы в классических системах. Кроме поступательного движения этому закону подчиняется и вращательное движение. Особый случай представляет колебательное движение, где на каждую степень свободы приходится энергия – kT .
Установим связь между внутренней энергией газа E и его давлением
p = NkT V . Поскольку kT = 2ε |
3 (2.13), то давление |
|
||
p = |
2 N ε |
= |
2 E |
(2.15) |
|
3 V |
|
3 V |
|
оказывается численно равным 2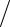 3 кинетической энергии поступательного
3 кинетической энергии поступательного
движения молекул газа, находящихся в единице объема.
Вычисления среднего квадрата энергии (2.7) и её квадратичной
флуктуации (∆ε2 = ε2 −ε2 ) дают:
73
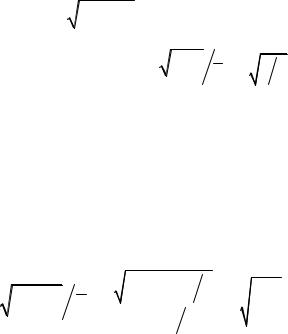
|
|
∞ |
2 |
|
|
∞ |
ε |
|
15 |
|
|
||||
ε2 = ∫ ε2dw(ε) = |
|
|
|
∫e− |
|
ε5/2dε = |
(kT)2 |
; |
|||||||
|
|
|
kT |
||||||||||||
|
|
3 |
|
4 |
|||||||||||
0 |
|
|
π(kT) |
0 |
|
|
|
|
|
|
|||||
|
|
|
= 3 (kT)2 ; |
|
|
|
ε = 2 3 . |
|
|||||||
|
|
∆ε2 |
|
δ = ∆ε2 |
|
||||||||||
2 |
|
|
|
ε |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
Большая относительная флуктуация обусловлена тем, что оно относится к отдельной молекуле. Если же рассматривать газ из N молекул, то его средняя энергия, дисперсия и относительная флуктуация оказываются равными
E = 3NkT / 2 ; |
|
|
|
= ∑ |
|
= |
3 N(kT)2 |
; |
||||
(∆E)2 |
(∆εj )2 |
|||||||||||
|
|
|
|
|
j |
|
|
2 |
|
|
||
|
|
|
|
|
3N(kT)2 2 |
|
|
|
2 |
. |
(2.16) |
|
δ = (∆E)2 |
E = |
|
= |
|
||||||||
|
|
|
|
|||||||||
|
|
|
|
|||||||||
E |
|
|
|
3NkT 2 |
|
|
|
3N |
|
|||
|
|
|
|
|
|
|
|
|
||||
В этом случае отличие истинного значения энергии от его среднего ничтожно мало при всех реальных значениях N . Следовательно можно с большой степенью точности считать энергию идеального газа равной ее среднему значению.
2.5. Столкновение молекул между собой
Выделим две молекулы идеального газа с массами m1 и m2 и
скоростями vG1 и vG2 . Вопрос о столкновении этих молекул связан с характером их относительного движения. В механике показывается, что движение двух частиц можно всегда разложить на движение в пространстве общего центра тяжести и их относительное движение. Из определения скоростей относительного uG и абсолютного (центра тяжести двух молекул) vG движения, а именно:
|
|
uG = vG |
−vG |
; |
|
|
||
|
|
|
1 |
|
2 |
|
|
|
MvG = m vG |
+m vG |
; |
M = m +m |
. |
||||
1 |
1 |
2 |
2 |
|
|
1 |
2 |
|
Находим зависимость vGi (vG,uG) и кинетическую энергию
74
|
|
|
|
|
|
|
|
G |
|
|
G |
|
|
|
|
|
m2 |
|
|
G |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
v1 |
= v |
+ |
|
|
|
|
|
u; |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
m1 +m2 |
|
|
|
|
|
|
|
|
|
(2.17) |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
G |
|
|
|
G |
|
|
|
|
|
m1 |
|
|
G |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
v2 |
= v |
− |
|
|
|
|
|
u; |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
m1 +m2 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
m v |
|
|
m v |
|
|
|
m |
|
|
|
|
m |
2 |
|
|
|
|
|
m |
|
|
|
|
|
|||||
T = |
+ |
|
|
= |
|
|
|
2 |
|
|
u |
2 |
+ |
2 |
|
|
|
|
GG |
+ |
||||||||||||
1 1 |
|
2 2 |
|
|
1 |
|
v |
+ |
|
|
|
|
|
|
2 |
|
vu |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
2 |
|
|
2 |
|
|
2 |
|
|
|
M |
|
|
|
|
|
|
M |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m |
|
|
|
m |
2 |
|
|
|
|
|
m |
|
|
Mv2 |
|
µu2 |
|
|
|
|
|||||||||||
|
2 |
|
2 |
|
|
2 |
|
|
|
GG |
|
|
|
|
|
|
||||||||||||||||
+ |
|
|
|
|
|
1 |
|
u −2 |
|
|
1 |
|
vu |
= |
|
|
|
|
+ |
|
|
|
|
, |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
v + |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
2 |
|
|
M |
|
|
|
|
|
|
M |
|
|
2 |
|
|
|
2 |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где µ = m1m2 / M |
|
– |
приведенная |
|
|
масса. |
Первое |
|
|
слагаемое определяет |
||||||||||||||||||||||
энергию движения центра тяжести, а второе – энергию относительного движения. Относительное движение происходит так, как если бы одна из молекул была неподвижна, а вторая имела массу, равную приведенной µ.
Вероятность того, что одна молекула имеет скорость v1 , а вторая – v2 ,
равна произведению вероятностей простых событий, т.е.
|
|
|
|
|
|
|
|
|
|
|
|
m1 |
3/2 |
|
|
|
m1v12 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
2 |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
2kT |
|
|
|
|||||||||
dw(v ,v ) = dw(v )dw(v ) |
= |
4π |
|
|
|
e |
|
|
|
|
v dv |
|
× |
|||||||||||
|
|
|
|
|
|
|
||||||||||||||||||
1 |
2 |
|
|
|
1 |
|
2 |
|
|
2πkT |
|
|
|
|
|
|
1 |
1 |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
3/2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
µu2 |
|
|
|
|||
|
m |
|
|
e |
− |
m2v2 |
2 |
= |
|
µ |
|
3/2 |
|
− |
× |
|
|
|||||||
|
|
|
|
|
|
|||||||||||||||||||
×4π |
|
2 |
|
|
2kT |
|
v2dv2 |
4π |
|
|
|
e |
|
|
2kT |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2πkT |
|
|
|
|
|
|
|
|
2πkT |
|
|
|
|
|
|
|
|
|
|||||
|
N |
3/2 |
|
−Mv2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
2kT |
|
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
×4π |
|
|
|
e |
|
|
v1dv1 |
v2dv2. |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2πkT |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Перейдем в фазовом пространстве от переменных (v1,v2 ) к переменным
(u,v):
v12dv1v22dv2 = u2du v2dv ,
где учтено, что модуль якобиана преобразования равен D(v1,v2 ) D(u.v) =1.
Искомая вероятность dw(v1,v2 ) распадается на произведение dw(v) и
75

|
|
3/2 |
|
|
µu2 |
|
|
|
µ |
|
|
− |
|
2 |
|
|
2kT |
|
|||||
dw(u) = 4π |
|
|
e |
|
|
u du. |
(2.18) |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
2πkT |
|
|
|
|
|
|
Для упрощения считаем, что газ состоит из одинаковых молекул, µ = m / 2 .
Используя указанное распределение, найдем среднюю скорость относительного движения
|
|
|
∞ |
|
µ |
3/2 |
∞ − |
µu2 |
|
|
|
|
|
|
|
|
∫ |
|
|
∫ |
|
2kT |
3 |
|
|
|
|
|
|
|
|
|
|
|
|||||||
u = |
udw(u) = 4π |
|
|
e |
|
u du = 2v , |
(2.19) |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
0 |
|
2πkT |
0 |
|
|
|
|
|
|
|
которая оказывается в 2 раза больше средней скорости теплового движения молекул газа.
В дальнейшем предполагаем, что газ настолько разрежен, что молекулы сталкиваются попарно, а числом столкновений, при котором одновременно приходят в непосредственный контакт три и более молекул будем пренебрегать. Соударение двух молекул – сложный процесс, зависящий от природы и характера их взаимодействия. Если молекулы рассматривать как твердые шарики радиуса r , взаимодействующие только при непосредственном контакте, то для соударения центры молекул должны были бы сблизиться на расстояние d = 2r . Иными словами, соударения происходят в том случае, когда центры сталкивающихся молекул лежат в
круге площадью σr = 4πr2 . Эту площадь называют геометрическим сечением соударения. В реальных газах молекулы начинают
взаимодействовать |
еще до |
непосредственного |
контакта, |
на расстояниях |
||
def |
> 2r . Это расстояние называют эффективным диаметром столкновения, |
|||||
а |
площадь круга |
σ |
= πd2 |
– эффективным |
сечением |
соударения. При |
|
|
ef |
ef |
|
|
|
сильном взаимодействии между молекулами, эффективное соударение может, во-первых, существенно превышать геометрическое, во-вторых, зависеть от ряда факторов и прежде всего от относительной скорости сближающихся частиц. Будем считать, что все молекулы газа неподвижны, кроме одной, которая двигается со скоростью u . Она проходит в единицу
76

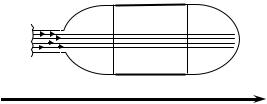
времени путь u , вырезая в пространстве цилиндр объемом σu (рис. 2.5). При этом она испытывает столкновения со всеми неподвижными молекулами, находящимися в этом цилиндре. Их количество и определяет число соударений:
|
dν(u) = σ u ndw(u), |
|
σ |
где n – общая плотность молекул газа. |
|
u |
Полное число соударений, испытываемых |
|
молекулой в единицу времени, вычисляется |
||
|
uпутем интегрирования этого выражения по всем возможным значениям u :
Рис. 2.5. |
∞ |
ν = ∫ σ u ndw(u) |
|
|
0 |
Если сечение σ не зависит от относительной скорости, то с учетом (2.18) и (2.19) имеем
|
µ |
3/2 |
∞ |
|
− µu2 |
|
|
|
|
|
|
|
|
|
|
∫ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2kT |
3 |
|
|
|
|
|
|
|
ν = 4πσn |
|
|
|
e |
|
|
u du = nσu = 2nσv , |
(2.20) |
|||||
|
2πkT |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
kT |
1/2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
(2.21) |
||||||
|
|
ν = 4nσ |
|
. |
|||||||||
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
πm |
|
|
|||||
Это и есть число столкновений, испытываемое молекулой в 1 сек. Оно растет с увеличением температуры, плотности газа, размерами молекул и уменьшением их массы.
2.6. Длина свободного пробега
Средний путь, проходимый молекулой между двумя последовательными соударениями, называется средней длиной свободного пробега. За одну секунду молекула проходит в среднем расстояние, равное средней тепловой скорости v . За это время она испытывает ν столкновений (2.21); и средняя длина свободного пробега оказывается обратно пропорциональна плотности газа и эффективному сечению σ:
77

λ = |
|
|
1 |
|
|
v |
= |
(2.22) |
|||
|
|
|
|||
ν |
|
2nσ |
|
||
Практический интерес представляет вероятность того, что |
молекула |
||||
пройдет произвольный путь x , не испытав ни одного столкновения, или, иными словами, закон распределения вероятностей для пробега молекул. Обозначим искомую вероятность через w(x) . Тогда w(x +dx) – вероятность
безстолкновительного прохождения пути x +dx . Это событие сложное,
состоящее из двух независимых, поэтому, согласно теореме умножения вероятностей,
w(x +dx) = w(x) w(dx).
Очевидно, что вероятность wc (dx) , что на бесконечно малом отрезке пути dx
молекула |
испытает |
соударение, |
пропорциональна |
его |
длине, т.е. |
wc(dx) = adx или |
w(dx) = 1 −wc(dx) = 1 −adx . После |
представления |
|||
w(x +dx) |
рядом по степеням dx [w(x +dx) w(x) + |
∂w dx... ] исходное |
|||
|
|
|
|
∂x |
|
уравнение и его решение примут вид |
|
|
|
||
|
dw(x) dx = −aw(x); |
w(x) = Aexp(−ax) . |
|
||
Событие – пролёт молекулой сколь угодно малого пути без столкновений
считаем |
достоверным |
w(x → 0) = 1 , откуда следует |
A = 1 и искомая |
вероятность |
|
|
|
|
|
w(x) = e−ax |
(2.23) |
Согласно определению, средняя длина свободного пробега есть |
|||
|
|
∞ |
|
|
|
λ = ∫ xdP , |
|
|
|
0 |
|
где dP |
– вероятность |
столкновения на интервале dx |
(= wc(dx)) после |
безстолкновительного прохождения расстояния x (= w(x)), т.е.
dP = w(x)wc(dx) = ae−axdx .
78
Интегрирование дает
∞
λ = ∫ xe−axadx = a−1 .
0
Таким образом, вероятность того, что молекула пролетит путь x , не испытав ни одного столкновения, равна
w(x) = e−x /λ . |
(2.24) |
Данное распределение является функцией средней длины свободного пробега и не зависит от координат места последнего столкновения. Это означает, что расстояние x отсчитывается от произвольной точки, а не от места последнего столкновения. Полученная формула лежит в основе экспериментального определения средней длины свободного пробега молекул в газе.
|
|
|
|
|
|
|
|
|
Представим |
себе узкий |
направленный |
|
|
|
|
|
|
|
|
|
|
пучок молекул, входящий в некоторый |
|||
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
откачанный до низкого давления сосуд с |
|||
|
|
|
|
|
|
|
|
x |
двумя охлаждаемыми полупрозрачными |
|||
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
пластинами |
(решетки), |
помещенными |
|||
|
|
|
|
|
|
|
|
|||||
x |
1 |
|
|
x2 |
||||||||
Рис. 2.6. |
|
|
|
|
на расстояниях x1 |
и x2 от входного |
||||||
|
|
|
|
отверстия |
(Рис. |
2.6). |
Молекулы, |
|||||
|
|
|
|
|
|
|
|
|
||||
пролетевшие путь x1 и x2 без соударений, оседают на пластинах в виде слоев. Путем измерения их толщин (пропорциональных плотности частиц,
осевших на пластине) определяется отношение числа частиц на пластинах x1
и x2 . Учитывая, что N (x) ~ w(x) и формулу (2.24) находим среднюю длину свободного пробега из соотношения
N(x1) |
|
|
x −x |
2 |
|
|||
|
=e− |
1 |
. |
|||||
|
λ |
|
||||||
|
||||||||
N(x |
2 |
) |
|
|
|
|
||
|
|
|
|
|
|
|
||
По порядку величины λ составляет около 10 см при p ≈ 10−3 мм. рт. ст. и
около 10−5 см при атмосферном давлении. 79
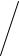
2.7. Идеальный газ во внешнем поле
2.7.1. Распределение Больцмана . При помещении газа во внешнее поле каждая молекула помимо кинетической приобретает еще и потенциальную энергию, которая в общем случае является функцией
координатU(qG):
ε(pG,qG) = ε(pG) +U(qG) .
Подстановка суммарной энергии в каноническое распределение Гиббса
определяет вероятность того, |
что молекула имеет значение импульса pG и |
||||||||
находится в окрестности точки с радиус-вектором qG: |
|||||||||
G G |
|
e |
− |
ε(p)+U (q) |
G G |
||||
|
|
|
|
kT dpdq |
|||||
dw(p,q ) = |
|
|
|
|
|
|
. |
||
∫ ∫e |
− |
ε(p)+U (q) |
G G |
||||||
|
|
|
|||||||
|
|
|
kT |
dpdq |
|||||
(p) (q)
Здесь интегрирование ведется по всем возможным значениям переменных. Поскольку кинетическая энергия молекулы идеального газа зависит от
импульса, а потенциальная от координат, последнюю формулу можно представить двумя сомножителями
|
|
|
ε(p) |
|
U (q) |
|||||
G G |
G |
G |
e− kT dpG |
|
e− |
|
|
dqG |
||
|
kT |
|||||||||
dw(p,q ) = dw(p)dw(q ) = |
|
|
|
|
. |
|||||
ε(p) |
|
U (q) |
||||||||
|
|
|
∫e− kT dpG |
∫e− |
|
dqG |
||||
|
|
|
kT |
|||||||
|
|
|
(p) |
|
(q) |
|||||
Первый из множителей – ранее полученное распределение Максвелла. Второй
– вероятность нахождения молекулы в элементе объема dV ≡ dqG, которая зависит от потенциальной энергии молекулы во внешнем поле. Когда внешнее поле отсутствует последний множитель сводится к отношению dV /V .
Распределение молекул в пространстве в поле внешних сил
dw(qG) =e− |
U (q) |
dqG ∫e− |
U (q) |
dqG |
(2.25) |
kT |
kT |
||||
|
|
(q) |
|
||
называют распределением Больцмана.
80
На основе теореме умножения вероятностей указанное распределение можно рассматривать как произведение вероятности двух независимых событий. Это обстоятельство выражает не очевидное важное свойство молекул идеального газа: значение ее импульса совершенно не зависит от ее положения в пространстве. Распределение молекул по импульсам (или скоростям) не изменяется от того, находится ли газ в поле внешних сил или нет. Независимость распределения молекул по координатам и импульсам позволяет рассматривать каждое из них в отдельности.
2.7.2. Идеальный газ в гравитационном поле . Применим распределение Больцмана к газу, который находится в гравитационном поле (земного тяготения). Направим ось z вертикально вверх. Тогда потенциальная энергия газовой молекулы массы m будет равна U = mgz . Поскольку U(z) зависит только от высоты, в плоскости z = const
молекулы распределены равномерно. Интерес представляет лишь зависимость распределения вероятностей от координаты z
|
e |
−mgz |
|
dw(z) = |
kT dz |
(2.26) |
|
|
mgz |
||
|
|
|
|
|
∫e− kT dz |
|
|
где интеграл берется по всем возможным значениям z . Вводя вместо распределения вероятностей среднее число частиц в единице объема (плотность) dn(z) наданнойвысотепоследнююформулуможнопереписатьввиде
mgz |
|
dn(z) = n e− kT dz |
(2.27) |
0 |
|
где n0 – плотность частиц на условном уровне отсчета координаты,
например, в плоскости z = 0 . Формула показывает, что плотность газа в поле тяжести убывает по экспоненциальному закону. Она уменьшается в e
раз на характеристической длине распределения частиц в поле тяжести
81
