
Метода термодинамика(лекции)
.pdf
|
|
|
|
E =T +U = m |
N −1 |
|
|
|
|
|
|
æ |
N −1 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
∑uj2 + |
∑(uj +1 −uj )2 , |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
j =0 |
|
|
|
|
|
|
2 |
j=0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
где суммирование ведется по всем атомам цепочки. Подстановка u |
2 |
дает |
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
j |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m |
|
|
|
|
∑∑∑ n n |
|
( |
|
) |
|
( |
|
′ ) |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
naj |
|
|
|
|
|
|
|
|
|
|
|
′ |
n |
|
n |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
T = |
|
|
∑ ∑ n |
sinq |
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
aj . |
||||||||||||||||||||||||||
|
N −1 j |
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
N |
−1 j |
|
n |
|
|
n′ |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
После изменения порядка суммирования |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
m |
|
∑∑ n n′ |
|
|
|
2 |
|
|
|
∑ |
|
|
( n ) |
|
|
( n′ |
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
) |
|
|
|
|
|
|||||||||||||||||||
|
|
|
T = |
|
|
|
|
|
|
|
|
|
η |
|
η |
|
|
|
|
|
|
|
|
|
|
|
sin q aj |
sin q aj |
|
. |
|
|
|
|
|||||||||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
N − |
1 |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
n |
|
n′ |
|
|
|
|
|
j |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
В силу ортогональности синусов |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0, n ≠ n′ |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
∑ |
|
|
|
|
( n |
) |
|
|
( |
n |
′ |
|
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
N −1 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
sin |
q aj |
|
sin q |
aj |
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
j |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, n = n′ |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
имеем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T = m |
|
∑ηn2 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Для определения потенциальной энергии вычислим |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
uj +1 −uj = |
|
|
N −1 |
∑ηn {sin qna(j |
+1) −sin(qnaj)}= |
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
qna |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
= |
|
|
|
|
|
∑ηn 2 cos qna j + |
|
|
|
sin |
|
|
|
|
= |
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
N −1 |
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
2 |
|
|
|
|
m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
η ω |
cosq a |
j + |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
N −1 |
|
|
|
|
|
∑ n |
n |
|
|
|
|
n |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
æ n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Поступая так же, как при вычислении кинетической энергии, с учетом ортогональности косинусов получаем
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
æ |
|
2 |
|
|
|
|
|
|
|
|
|
|
m |
|
|||
|
|
|
|
|
|
|
|
1 |
|
|
1 |
|
2 2 |
|||||
U = |
|
∑∑∑ηnηn′ωnωn′ |
|
|
|
|
cos qna j + |
|
cos qn′a j + |
|
= |
|
∑ωnηn. |
|||||
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
j n n′ |
|
N −1 |
|
|
|
2 |
|
|
|
|
2 |
n |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таким образом, полная энергия одномерного кристалла |
|
|
|
|
|
|||||||||||||
|
|
|
E = m ∑(ηn2 |
+ ωn2ηn2 ) |
|
|
|
|
|
(4.8) |
||||||||
|
|
|
|
|
2 |
n |
|
|
|
|
|
|
|
|
|
|
||
172

выражается квадратичной формой (~η |
2, η2 ). Каждое слагаемое |
|
|
n |
n |
|
|
εn = m (ηn2 |
|
+ ωn2ηn2 ) 2 |
(4.9) |
представляет энергию линейного гармонического осциллятора с массой,
равной массе атома, колеблющегося с частотой ωn . Энергия кристалла из N
атомов, совершающих связанные колебания, оказывается равной энергии N независимых гармонических осцилляторов. В этом смысле кристалл из N
связанных атомов эквивалентен набору N независимых осцилляторов с
частотами ωn . Вместо того, чтобы находить среднюю энергию сложной системы колеблющихся связанных атомов, можно ее определить из простой эквивалентной системы – набора независимых осцилляторов. Каждый осциллятор – одно из нормальных колебаний кристалла, в котором участвуют все атомы.
В квантовой механике энергия линейного осциллятора принимает дискретный ряд значений:
|
|
|
|
|
1 |
|
|
|
|
|
|
ε |
(s) = =ω |
|
|
+ |
|
, |
s |
|
= 0, 1, 2, ..., ∞, |
(4.10) |
|
s |
|
|
|
|
|||||||
n |
n |
n |
|
2 |
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где sn – квантовое число, ωn |
– классическая частота, связанная с постоянной |
||||||||||
упругой силы и массой атома. Энергетический спектр осциллятора состоит из совокупностей дискретных уровней, отстоящих друг от друга на величину
=ωn . Минимальная порция (квант) энергии εφ = =ωn = hνn , которую может
поглотить (испустить) кристалл при тепловых колебаниях, называется фононом. В таких процессах происходит переход возбуждаемого нормального колебания с данного уровня на ближайший соседний. Поле упругих волн можно трактовать как газ, образованный квантами нормальных колебаний решетки – фононами, обладающими энергией εφ = =ωn и
импульсом pφ = =ωn v = =qn = h λn . Иными словами, нагретый кристалл можно уподобить ящику, заполненному фононным газом.
173

4.4. Статистическая сумма и энергия кристалла (в гармоническом приближении)
Уровни энергии всего кристалла совпадают с уровнями энергии набора 3N независимых гармонических осцилляторов. Общая энергия есть сумма слагаемых вида (4.10), где n принимает значения n = 1,2,..., 3N . Если U0 –
потенциальная энергия кристалла в равновесном состоянии, то энергия колебаний всех осцилляторов кристалла в соответствующих состояниях s1 , s2 , …, s3N равна:
|
|
3N |
|
3N |
|
Es1,s2 ,s3 ,...,s3N |
=U0 |
+ ∑hνn (sn + |
1 |
)= E0 + ∑hνnsn , |
(4.11) |
2 |
|||||
|
|
n=1 |
|
n=1 |
|
3N |
|
|
|
|
|
где E0 =U0 + ∑hνn / 2 – |
есть энергия |
нулевых колебаний. |
Состояние |
||
n=1
каждого осциллятора (n -ой моды нормальных колебаний) определяется полным набором целых чисел. Сумма по всем этим состояниям в ансамбле осцилляторов дает функцию состояний кристалла
∞ ∞ |
∞ |
Es1 ,s2 ,...,s3N |
Z = ∑∑... ∑e− |
kT |
|
s1 =0 s2 =0 |
s3N =0 |
|
E0 3N ∞ |
hνn |
E0 3N |
|
|
|
1 |
|
|
|
=e−kT ∏∑e− kT s |
=e−kT ∏ |
|
|
|
|
|
; |
||
1 |
−e |
−hν |
n |
kT |
|||||
n=1 s=0 |
|
n=1 |
|
|
|
||||
|
|
|
3N |
|
kT ). |
|
||
ln Z = −E0 |
kT −∑ln(1 −e−hνn |
(4.12) |
||||||
|
|
|
n=1 |
|
|
|
|
|
Отсюда легко найти свободную и внутреннюю энергии |
|
|||||||
|
|
|
3N |
|
|
|
|
|
F = −kT ln Z = E0 +kT ∑ln(1 −e−hνn kT ), |
(4.13) |
|||||||
|
|
|
n=1 |
|
|
|
|
|
|
∂ |
|
3N |
hνn |
|
|
||
E = kT 2 |
|
ln Z = E0 + ∑ |
|
. |
(4.14) |
|||
∂T |
|
hν kT |
||||||
|
n=1 e |
n |
−1 |
|
||||
Каждое слагаемое в сумме имеет смысл средней энергии осциллятора n -ой моды
εn = hνn f (hνn ) . |
(4.15) |
174

Рис. 4.3
Функция
f (hνn ) = (ehνn kT −1)−1 |
(4.16) |
определяет среднее число фононов (распределение Бозе-Эйнштейна). От тепловой энергии kT зависит число возбуждаемых фононов данной частоты
hνn .
При температуре T в решетке возбуждаются все нормальные колебания вплоть до колебания с энергией hνn kT , колебания с энергией hνn > kT
практически не возбуждаются (Рис. 4.3,а). На рис. 4.3,б горизонтальными черточками отмечены энергетические спектры нормальных колебаний, имеющие частоты
νn(1) = kT 8h , νn(2) = kT
8h , νn(2) = kT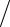 4h , νn(3) = kT
4h , νn(3) = kT 2h , νn(4) = kT
2h , νn(4) = kT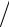 h , νn(5) = 2kT
h , νn(5) = 2kT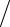 h .
h .
Видно, что колебание νn(1) возбуждено до 8-го уровня, νn(2) – до 4-го, …, а νn(5)
вообще не возбуждается при данной температуре.
К сожалению, приведенные формулы, кроме качественных оценок свойств кристалла, не позволяют делать количественные расчеты. Трудности заключаются в том, что частоты νn остаются неизвестными, их определение для обобщающей модели кристалла – ключ к построению его статистико-
175

механической теории. В принципе для отдельных тел νn можно определить из дисперсионного уравнения с учетом силовых постоянных. Недостаток такого подхода в том, что, во-первых, силовые параметры для большинства реальных кристаллов измерены с большой погрешностью, с другой стороны, в необходимости проводить численные расчеты для каждого отдельного кристалла. Таким образом, теряется простота и общность результатов статистической термодинамики, фундаментальность которой основана на едином наборе обобщающих уравнений.
Модель Эйнштейна. В общем случае при определении спектра нормальных колебаний произвольных систем использовались упрощающие модели. Согласно приближенной модели Эйнштейна, каждый атом, колеблющийся в узле кристаллической решетки, отождествлялся с квантовым осциллятором, имеющим три степени свободы. В кристалле с атомами одного сорта все атомы совершенно равноправны и колеблются независимо друг от
друга с одинаковой частотой νE . В этом случае энергия линейного гармонического осциллятора равна ε = hνE (s +1 / 2), а его функция состояния
|
hνE (s+1/2) |
e |
− |
hνE |
|
|
|
|
|||||
z = ∑e− |
2kT |
|
|
. |
|||||||||
kT |
= |
|
|
|
|
|
|
||||||
|
|
|
|
|
hν |
|
|||||||
s |
1 |
−e |
− |
|
|
E |
|
|
|||||
2kT |
|||||||||||||
|
|||||||||||||
|
|
||||||||||||
Средняя энергия колебательного движения атома с одной степенью свободы и кристалла из N атомов равны
ε = kT 2 |
∂ |
ln z = |
hνE |
+ |
|
hνE |
|
(4.17) |
∂T |
|
ehνE kT |
|
|||||
|
2 |
|
−1 |
|||||
E = 3N ε = |
3NhνE |
+ |
3NhνE |
. |
|
|
|||
|
2 |
ehνE kT −1 |
||
Непосредственно дифференцируя (4.18), получаем формулу Эйнштейна
|
|
|
|
2 |
|
|
|
hνE kT |
|
|
||
|
|
|
|
|
|
|
e |
|
|
|||
|
|
∂E |
hνE |
|
|
|
|
|
||||
C |
= |
|
= 3NK |
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
2 |
||||||
V |
|
∂T |
|
|
|
|
hν |
|
kT |
|
|
|
|
kT |
(e |
|
−1) |
|
|
||||||
|
|
V |
|
|
|
|
E |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
||
(4.18)
(4.19)
176

При высоких температурах (hνE << kT ) значение теплоемкости соответствует закону Дюлонга и ПтиCV = 3NK ; а при низких температурах (hνE >> kT )
CV 3NK hνE 2 e−hνE  kTkT
kTkT
уменьшается экспоненциально. Хотя модель Эйнштейна сильно упрощает реальную ситуацию в кристалле, формула (4.19) хорошо описывает экспериментальные данные. Серьезные расхождения наблюдаются лишь при очень низких температурах. В эксперименте, уменьшение теплоемкости происходит по закону T 3 .
4.5. Теория теплоемкости Дебая
4.5.1. Спектральная плотность нормальных колебаний . Исключительно плодотворным оказывается подход, при котором сумма в (4.13)-(4.14) заменяется интегралом. Вводится функция распределения частот (спектральная плотность) g(ν) так, что g(ν)dν
равняется числу мод, частоты которых лежат в интервале от ν до ν +dν .
Посколькуполноечисломодравно 3N , условиенормировкиимеетвид
∞ |
|
∫ g(ν)dν = 3N . |
(4.20) |
0 |
|
При таком определении g(ν) следует представить все суммы от частотно зависимых слагаемых, например, (4.13), (4.14), интегралом с весовой функцией
∞ |
|
∑f (νn ) = ∫ g(ν)f (ν)dν . |
(4.21) |
n |
0 |
|
Задачасводитсякнахождениюспектральнойплотностинормальныхколебаний Она легко решается в модели П.Дебая. Эта модель предполагает, что частоты нормальных колебаний кристалла распределены так же, как частоты изотропной упругой непрерывной среды, а не системы отдельных частиц.
177
Такое допущение хорошо выполняется в длинноволновом диапазоне, когда в колебаниях участвуют одновременно (синфазно) много атомов, и дискретный характер среды не учитывается. Такой вывод непосредственно вытекает из анализа дисперсионного уравнения (4.5)-(4.7). Иная ситуация возникает в области высоких частот, где скорость распространения волны зависит от частоты. Кроме того, дискретный характер структуры кристалла ограничивает число колебаний: волны, длина которых меньше межатомных расстояний (λ <a ), не возбуждаются. Последнее затруднение легко снимается введением обрезающей частоты, выше которой не существуют колебания; однако наличие дисперсии скорости их распространения при высоких частотах в модели Дебая игнорируется.
Предположим, что твердое тело имеет форму куба с ребром L = aN . Поскольку кристалл отождествляется с упругой непрерывной средой, то в нем возбуждаются только волны, половина длины которых укладывается целое число раз между гранями куба (nλ / 2 = aN = L ), т.е. с проекциями волнового вектора
|
q |
|
= |
πnx |
, |
q |
|
|
= |
πny |
, |
|
q |
|
= |
πnz |
, |
n |
|
= 1,2,...,N |
|
|||||||||||
|
x |
|
y |
|
|
z |
|
|
j |
|
||||||||||||||||||||||
|
|
|
aN |
|
|
|
|
aN |
|
|
|
|
|
|
|
|
aN |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
и частотами |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ω |
,ny ,nz |
= a æ q |
2 |
+q2 |
+q2 |
= a æ q . |
|
||||||||||||||||||||||
|
|
|
|
nx |
|
|
|
|
|
m |
|
|
x |
|
|
|
|
y |
|
z |
|
|
|
m |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Разность |
между |
соседними |
|
|
|
|
|
проекциями |
|
|
|
волнового вектора |
||||||||||||||||||||
∆q0 = qj (nj |
+1) −qj (nj ) = π / aN . |
|
|
|
Число |
нормальных |
колебаний в |
|||||||||||||||||||||||||
интервале соответствующих проекций волнового вектора ∆qj |
и общее число |
|||||||||||||||||||||||||||||||
осцилляторов в трехмерной структуре будут равны |
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
∆n |
j |
= ∆q |
j |
|
∆q |
0 |
= aN |
∆q |
, |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
π |
|
|
j |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
∆n |
∆n |
∆n |
|
= |
(aN )3 |
|
∆q |
∆q |
∆q |
|
. |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
π3 |
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
x |
|
|
|
y |
|
|
z |
|
|
|
|
|
|
|
|
x |
|
y |
|
|
z |
|
|
|||
178

Для непрерывного спектра частот (модель сплошной среды!) элемент объема в пространстве волновых чисел запишем в сферической системе координат с учетом, что все они находятся в положительном октанте (∆qj > 0 , ∆nj > 0 ):
|
(aN )3 |
2 |
4πV |
2 |
|
g(q)dq = |
|
4πq dq = |
|
q dq . |
(4.22) |
π3 |
8π3 |
В трехмерной среде возбуждаются три волны упругих колебаний, одна из которых является продольной, а две – поперечными:
g(ν)dν = gl (ν)dν +2gt (ν)dν.
где gl (ν) и gt (ν) – функции распределения частот продольных и поперечных колебаний, соответственно. Волновые числа связаны с фазовыми скоростями
(vl , vt ) и частотой соотношениями qtvt = qlvl = 2πν. После замены в (4.22) q
на ν находим
g(ν)dν = 4πV v1l3 + v2t3 ν2dν.
Чтобы в модели Дебая ввести ограничение на частотный диапазон возбуждаемых нормальных колебаний (ν ≤ νmax ), воспользуемся условием нормировки (4.20) в виде
|
νmax |
|
|
|
|
|
|
|
|
4πV 1 |
|
|
|
|
2 |
3 |
|
|
|||||||||||||
3N = ∫ g(ν)dν = |
|
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
νmax , |
|
|||||||||||||
|
|
|
|
|
|
|
|
3 |
|
|
|
3 |
|
||||||||||||||||||
|
|
3 |
|
|
|
|
|
v |
|
|
|||||||||||||||||||||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
v |
|
|
|
|
t |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l |
|
|
|
|
|
|
|
|
|
||||||
откуда следует |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9N |
|
|
|
|
3 |
|
3 |
|
1/3 |
|
|
|
|
||||||||||
|
ν |
3 |
|
|
|
= |
|
|
|
|
|
vl |
|
vt |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
4πV |
|
|
2v3 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
max |
|
|
|
|
|
|
+v3 |
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l |
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
и функция распределения частот нормальных колебаний |
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
2 |
2 |
|
|
|
9N |
2 |
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
g(ν) = |
4πV |
|
|
|
|
+ |
|
|
|
ν |
|
|
= |
|
|
|
|
|
|
|
ν |
, |
|
|
|
ν ≤ ν ; |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
max |
|||
|
|
v |
|
|
|
v |
|
|
|
|
|
|
ν |
max |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
l |
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ν > ν . |
||||
|
0, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
max |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(4.23)
(4.24)
179
Наибольшая (предельная) частота νmax зависит только от измеряемых на опыте скоростей звука и пропорциональна плотности кристалла. Введение «усеченной» спектральной функции определяет термодинамические функции (параметры), которые в предельных случаях низких и высоких температур совпадают с экспериментальными данными с высокой точностью, а в области промежуточных температур имеют характер интерполяционных формул. Критерием высоких и низких температур является характеристическая температура Дебая:
hνmax = kθD |
(4.25) |
Если принять, что скорость звуковых волн находится вблизи 105 см/с, а
плотность |
N /V |
– 1023 атомов/см3, то |
частота νmax имеет |
порядок |
||
1012 ÷1013 |
с–1, а температура Дебая заключена в пределах от 50 до 5000К. |
|||||
При температурах Дебая в твердом теле возбуждается весь спектр |
||||||
нормальных колебаний, поэтому |
с дальнейшим |
повышением температуры |
||||
(T > θD ) |
новые |
нормальные |
колебания |
не |
возбуждаются. |
Действие |
температуры в этом случае сводится к увеличению степени возбуждения возрастанию средней энергии каждого из существующих нормальных колебаний. Температуры T > θD принято называть высокими, а T << θD –
низкими. Характеристическая температура Дебая тем больше, чем больше плотность кристалла и меньше масса атома. Она особенно велика у весьма твердых кристаллов, построенных из легких атомов, например, у бериллия (Be)
–10000К, и у алмаза (C) – 18600К.
4.5.2.Потенциал, энтропия и теплоемкость кристалла . В качестве начального уровня энергии примем U0 = 0 .
Подставляя функцию распределения частот по Дебаю (4.24) в общее выражение (4.21), для функции состояний (4.12) имеем
180
|
|
|
|
|
|
νmax |
|
|
|
|
|
|
−hν/2kT |
|
|
|
|
|
|
|
|
|
|||||||
|
|
9N |
|
|
|
|
|
|
e |
|
|
|
|
2 |
|
|
|
|
|||||||||||
ln Z |
= |
|
|
|
|
∫ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ν dν = |
|
|
||||
|
3 |
|
|
|
|
|
|
|
|
|
−hν/kT |
|
|
|
|||||||||||||||
ν |
|
|
ln |
−e |
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
max |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9N |
νmax |
|
hν3 |
2 |
|
|
|
|
|
|
9N |
|
|
νmax |
|
|
|
|
|
|||||||||
= − |
∫ |
|
|
|
|
|
dν − |
|
|
|
|
∫ ν2 ln(1 −e−hν/kT )dν, |
|
||||||||||||||||
3 |
|
|
|
2kT |
|
|
|
|
3 |
|
|
|
|||||||||||||||||
|
νmax |
0 |
|
|
|
|
|
|
|
|
|
|
νmax |
|
0 |
|
|
|
|
|
|
||||||||
или в переменных x = hν / kT |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T |
3 |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
9Nθ |
|
|
|
|
|
|
|
|
θD |
/T |
|
2 |
|
−x |
|
||||||||||
ln Z = − |
|
|
|
|
D |
|
|
|
|
|
|
|
|
|
|
|
∫ |
x |
|
ln(1 |
−e )dx. |
(4.26) |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
8T |
|
|
−9N |
θ |
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
D |
|
|
0 |
|
|
|
|
|
|||||
Аналитическое представление интеграла возможно только в случае низких и
высоких температур. При T << θD предел в интеграле заменяется на бесконечность, поскольку подынтегральная функция весьма мала при больших значениях аргумента
∞ |
2 |
ln(1 −e |
−x |
)dx = − |
x3 |
|
|
|
|
−x |
|
∞ |
|
1 |
|
∞ |
x |
3dx |
|
|
|
|
1 |
∞ |
|
x3dx |
|
|
|
π4 |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
∫ x |
|
|
|
ln(1 |
−e |
|
) |
|
|
− |
|
∫ |
|
|
|
|
|
|
|
= − |
|
∫ |
|
|
|
|
|
|
= − |
|
; |
|||||||||
|
|
3 |
|
|
|
3 |
e |
x |
|
|
|
|
|
3 |
e |
x |
−1 |
45 |
||||||||||||||||||||||
0 |
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
0 |
|
|
−1 |
|
|
0 |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
9NθD |
|
π |
4 |
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
ln Z = − |
|
|
|
|
|
+ |
|
|
N |
θ |
. |
|
|
|
|
|
|
|
|
|
|
(4.27а) |
|||||||||||
|
|
|
|
|
|
|
|
8T |
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
D |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
При высоких температурах (T >> θD , x <<1) используя асимптотику |
||||||||||||||||||||||||||||||||||||||||
ln(1 −e−x ) ln(x) имеем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
θD /T |
|
|
|
|
|
θD /T |
|
|
|
|
|
|
|
|
1 |
|
θ |
|
3 |
|
θ |
|
1 |
|
θ |
3 |
|
|
||||||||||
|
|
|
2 |
|
−x |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
∫ |
x ln(1 −e |
|
)dx = |
∫ |
x ln x dx = |
|
|
|
D |
|
ln |
|
D |
− |
|
|
|
D |
|
, |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
3 |
|
|
|
|
T |
9 |
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T |
|
|
|
T |
|
|
|
|
|||||||||||||||
|
|
0 |
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
ln Z = − |
9NθD |
−3N ln |
θD |
+N . |
|
|
|
|
|
|
|
|
|
(4.27б) |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
8T |
|
|
|
|
|
|
|
T |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Эти формулы позволяют находить и свободную энергию F = −kT ln Z при высоких и низких температурах:
|
|
π |
4 |
|
|
3 |
|
|
|
F = 9Nkθ |
/ 8 − |
|
T |
, |
при T << θ ; |
(4.28а) |
|||
|
|
NkT |
|
|
|||||
D |
|
5 |
|
θ |
|
|
D |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
D |
|
|
|
|
( |
D ) |
, |
D |
(4.28б) |
F = −NkT −3NkT ln T / θ |
при T >> θ . |
|||
181
