
матан
.pdf
Тогда поток |
Π равен: |
|
|
n |
|
n |
n |
Π=∑∆kΠ=dlim→0 |
∑(F (ξk ), ∆k S )=dlim→0 |
∑P(ξk ,ηk ,ζk )∆k Syz +Q(ξk ,ηk ,ζk )∆k Szx +R(ξk ,ηk ,ζk )∆k Sxy |
|
k=1 |
|
k=1 |
k=1 |
где |
cosαk |
|
∆k |
Syz |
– |
вектор |
ориентированной |
||||
∆k S =n(ξk )∆k S = cos βk |
∆k S = |
∆k |
Szx |
||||||||
|
cosγ |
|
|
∆ |
k |
S |
|
|
|
|
|
|
|
|
k |
|
|
|
xy |
|
|
|
|
компоненты которого |
представляют |
|
собой |
площади |
∆k Syz , ∆k Szx , ∆k Sxy |
||||||
частей Sk на координатные плоскости.
площади,
проекций
Полученный предел называется поверхностным интегралом по координатам от векторфункции F (r ) , по выбранной стороне ориентированной поверхности S+ , и обозначается
∫∫(F (r ), dS )=∫∫P(x, y, z)dydz +Q(x, y, z)dzdx + R(x, y, z)dxdy .
S+ S+
Он может быть сведен к следующему двойному:
|
∫∫( |
F (r ), dS |
) |
= |
∫∫( |
) |
|
∫∫( |
|
u v ) |
. |
|
|
|
|
F (r ), n(r ) dS = |
|
F (r (u, v)), r′, r′ dudv |
|||||
|
S+ |
|
|
|
S |
|
|
Ω |
|
|
|
В частном случае, когда |
|
S+ ={z = z(x, y), |
(x, y) D} – |
верхняя сторона графика |
|||||||
непрерывно дифференцируемой функции, интеграл равен: |
|
|
|||||||||
∫∫P(x, y, z)dydz +Q(x, y, z)dzdx + R(x, y, z)dxdy =
S+
=∫∫(−P(x, y, z)zx′ −Q(x, y, z)z′y + R(x, y, z))z=z(x, y) dxdy
D

Решения.
№ 40.1.
Π=∫∫(v(r ),dS )=→
S+
S+ ={z =xy, (x, y) D ={x2 + y2 ≤a2 }}
→=∫∫(−P(x, y, z)zx′ −Q(x, y, z)z′y + R(x, y, z))dxdy =∫∫(−y zx′ − z z′y + x)z=xy dxdy =
D |
|
|
|
|
|
|
|
|
|
|
|
|
D |
|
=∫∫(−y y − xy x + x)dxdy =−∫∫y2 dxdy +0 +0 =−∫∫y2 dxdy =→ |
|
|||||||||||||
D |
|
|
|
|
|
|
D |
|
|
|
D |
|
||
Учитывая “круговую” форму области D , перейдем к полярным координатам. |
||||||||||||||
Поскольку |
|
|
|
|
|
|
|
x2 + y2 =a2 →r =a , |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
то |
|
|
|
|
D ={x2 + y2 ≤a2 } → Ω={r ≤a}={0 ≤ϕ ≤2π, 0 ≤r ≤a}. |
|||||||||
|
|
|
|
|
||||||||||
Тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
→=−∫∫r2 sin2 ϕ r drdϕ =−2∫π ( ∫a r3 sin2 ϕ dr |
)dϕ =−2∫π sin2 ϕdϕ ∫a r3dr = |
|||||||||||||
Ω |
|
|
|
|
0 |
0 |
|
|
|
0 |
0 |
|||
2π |
1−cos 2ϕ |
a4 |
|
a4 |
|
|
|
|
|
|||||
=−∫ |
|
|
2 |
dϕ 4 |
=−π |
4 . |
|
|
|
|
|
|
||
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
№ 40.2. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
I =∫∫(ρ(r )v(r ),dS )=→ |
|
|
|
|
|
|
|
|
||||||
S− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
{ |
|
|
|
|
|
|
{ |
|
|
} |
|
|
S |
= z =x2 |
+ y2 , |
(x, y) D = |
x2 + y2 ≤a2 |
} |
|
||||||||
|
|
|
|
|
||||||||||
→=−∫∫(−P(x, y, z)zx′ −Q(x, y, z)z′y + R(x, y, z))dxdy = |
|
|||||||||||||
D |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
=−∫∫x y z (−z zx′ − x z′y + y) |
|
z=x2 +y2 |
dxdy = |
|
||||||||||
|
|
|||||||||||||
|
|
|
|
|||||||||||
D |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
=−∫∫x y (x2 + y2 ) (−(x2 + y2 ) 2x − x 2 y + y)dxdy =
D
=−∫∫(−2x2 y (x2 + y2 )2 −2x2 y2 (x2 + y2 )+ xy2 (x2 + y2 ))dxdy =
D
=0 +∫∫2x2 y2 (x2 + y2 )dxdy +0 =2∫∫x2 y2 (x2 + y2 )dxdy =→
|
D |
|
|
|
|
|
|
D |
|
|
|
|
Учитывая “круговую” форму области D , перейдем к полярным координатам. |
|
|||||||||||
Поскольку |
|
|
|
|
x2 + y2 =a2 →r =a , |
|
|
|||||
|
|
|
|
|
|
|
|
|||||
то |
|
|
D ={x2 + y2 ≤a2 } → Ω={r ≤a}={0 ≤ϕ ≤2π, 0 ≤r ≤a}. |
|
||||||||
|
|
|
|
|||||||||
Тогда |
|
|
|
|
|
|
2∫π ( |
∫a r7 cos2 ϕ sin2 ϕ dr )dϕ = |
2∫π cos2 ϕ sin2 ϕdϕ ∫a r7 dr = |
|||
→=∫∫r2 cos2 ϕ r2 sin2 ϕ r2 r drdϕ = |
||||||||||||
Ω |
|
|
|
|
|
|
0 |
0 |
|
0 |
0 |
|
2π |
1 |
2 |
a8 |
a8 |
2π |
1−cos 4ϕ |
|
|
a8 |
|
|
|
= ∫ |
4 sin |
|
2ϕdϕ 8 |
= 32 |
∫ |
2 |
|
dϕ = |
32 π. |
|
|
|
0 |
|
|
|
|
0 |
|
|
|
|
|
|
|
№ 40.3.
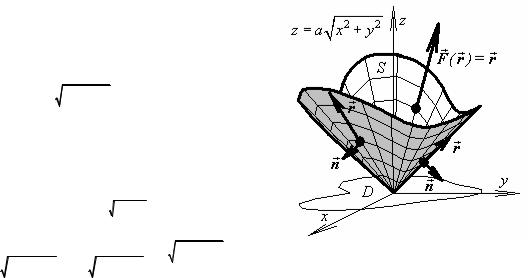
Из физических понятий очевидно, что поток вектора r через коническую поверхность равен нулю (вектор r “скользит” вдоль конической поверхности). Убедимся в адекватности математических формул интуитивным представлениям.
Π=∫∫(F (r ),dS )=∫∫(r ,dS )=→
S S
S ={z =a x2 + y2 , (x, y) D}
→=±∫∫(−P(x, y, z)zx′ −Q(x, y, z)z′y + R(x, y, z))dxdy =
|
D |
|
|
|
|
|
|
|
|
|
|
|
=±∫∫(−x zx′ − y z′y + z) |
|
z=a |
x2 +y2 |
dxdy = |
|
|
||||||
|
|
|
||||||||||
|
|
|
|
|||||||||
|
D |
|
|
|
|
|
|
|
|
|
|
|
|
∫∫D |
|
|
a x |
|
|
a y |
2 |
|
2 |
||
=± |
|
−x |
|
− y |
|
|
|
+a x |
+ y |
|
||
x2 + y2 |
x2 |
+ y2 |
||||||||||
|
|
|
|
|
|
dxdy = |
||||||
=±∫∫0dxdy =0.
D

№ 40.4.
Π=∫∫(F (r ),dS )=→
S+
|
u cos v |
|
|
||
S+ = |
r = u sin v |
|
|
, |
|
|
|
|
|
|
|
|
v |
|
|
||
|
|
|
|||
|
|
|
|
|
|
(0 ≤ u ≤ a, 0 ≤ v ≤ 2π)
→=∫∫(F (r ),ru′,rv′)dudv =∫∫(r ,ru′,rv′)dudv =→
Ω |
Ω |
|
cos v |
|
|
−u sin v |
|
||||
r′ = sin v |
|
, |
r′= |
u cos v |
|
|
|||
u |
|
|
|
|
v |
|
|
|
|
|
|
0 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
||
[ru′, rv′]= |
i |
j |
k |
cos v |
sin v |
0 |
|
|
−u sin v u cos v |
1 |
|
sin v
=−cos vu
|
|
|
|
|
u cos v |
|
|
|
sin v |
|
|
||||||||
|
|
(r ,ru′,rv′)=(r ,[ru′,rv′])=( |
|
|
|
|
, |
|
|
|
|
|
|
|
)=u v |
||||
|
|
u sin v |
|
|
−cos v |
||||||||||||||
|
|
|
|
|
|
v |
|
|
|
|
|
u |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
2π |
π |
2π |
π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
→=∫∫uvdudv = ∫( |
∫u v du |
)dv = ∫vdv ∫udu = |
1 |
2 |
|
2π |
1 |
|
2 |
|
π |
|
4 |
|
|||||
|
|
|
|
|
|||||||||||||||
2 v |
|
|
0 |
|
2 u |
|
|
0 |
=π |
|
. |
||||||||
Ω |
0 |
0 |
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
№ 40.5.
Π=∫∫(F (r ),dS )=∫∫ |
( |
r ,dS |
) |
=∫∫ |
|
r ,n dS = |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
( |
) |
|
|
|
|
|
||||||
S+ |
S+ |
|
|
|
|
|
|
|
|
S |
|
|
|
|
|
|
|
|
|
|
|
||
= n↑↑r (r ,n)= |
|
r |
|
|
|
n |
|
cos (r ,n)= |
|
r |
|
|
|
|
=r |
|
= |
||||||
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r S |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
=∫∫r0 dS =r0 ∫∫1 dS =r0 S.
S S

41. Сходимость несобственных интегралов
Условия.
Выяснить сходимость интегралов по неограниченному промежутку.
|
|
∞ |
|
|
|
x+1 |
|
|
|
|
|
|
|
∞ |
|
|
2x+1 |
|
|
|
|
|
|
|
|
|||||||||||
|
|
∫ |
|
|
|
|
|
|
|
|
∫ |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
№ 41.1. |
|
|
|
|
|
dx |
|
|
|
|
|
№ 41.1. |
|
|
|
|
|
|
|
dx |
|
|
|
|
||||||||||||
x3+2x+1 |
|
|
|
|
|
|
x4 +2x2 |
+1 |
|
|
|
|
||||||||||||||||||||||||
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∞ |
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
∞ |
|
3 x4 |
|
|
|
|
|
|
|
|
|
|
|||||
№ 41.2. |
∫ |
|
|
dx |
|
|
|
|
|
№ 41.2. |
∫ |
|
|
dx |
|
|
|
|
|
|
|
|
|
|||||||||||||
x2 −1 |
|
|
|
|
|
x2 −1 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∞ arctg x |
|
|
|
|
|
|
|
∞ arctg x2 |
|
|
|
|
|
|
|
|
||||||||||||||||||
№ 41.3. |
∫ |
|
|
|
3 x2 +1 dx |
|
|
|
|
|
№ 41.3. |
∫ |
|
|
3 x4 +1 |
|
dx |
|
|
|
|
|
||||||||||||||
|
|
1 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
||
|
|
∞ arctg |
|
|
|
|
|
|
|
|
|
|
∞ arctg |
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
∫ |
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
∫ |
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
||||
№ 41.4. |
|
|
|
|
|
dx |
|
|
|
|
|
№ 41.4. |
|
|
|
|
|
dx |
|
|
|
|
|
|||||||||||||
|
|
|
3 x2 +1 |
|
|
|
|
|
|
|
|
3 x+1 |
|
|
|
|
|
|||||||||||||||||||
№ 41.5. |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
№ 41.5. |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
∞ |
|
|
|
|
∞ |
ln x |
∞ |
ln x |
|
|
|
∞ |
|
|
|
|
∞ |
ln2 x |
|
∞ |
|
|
||||||||||||||
|
ln x |
|
, b) ∫ |
|
|
|
|
|
ln2 x |
dx , b) ∫ |
|
ln2 x |
|
|
||||||||||||||||||||||
a) ∫3 x4 dx |
|
x dx , c) ∫3 x |
dx |
a) ∫ 5 x4 |
|
|
x |
dx , c) ∫ 5 x7 |
dx |
|||||||||||||||||||||||||||
2 |
|
|
2 |
|
|
|
|
|
2 |
|
|
|
|
2 |
|
|
2 |
|
|
|
|
|
|
2 |
|
|
|
|||||||||
№ 41.6. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
№ 41.6. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
∞ |
|
|
|
|
|
|
|
∞ |
|
|
∞ |
∞ |
|
|
|
|
|
|
∞ |
1 |
∞ |
1 |
|
|||||||||||||
1 |
|
|
|
|
|
|
1 |
|
|
1 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
a) ∫ |
|
dx , b) ∫ |
|
dx |
, c) ∫ |
|
dx |
a)∫ |
|
dx , b)∫ |
|
dx , c)∫ |
|
dx |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
3 x4 ln x |
xln2 x |
5 x7 ln2 x |
||||||||||||||||||||||||||||||||||
xln x |
3 x ln x |
5 x4 ln2 x |
||||||||||||||||||||||||||||||||||
2 |
|
|
|
|
|
|
|
2 |
|
|
|
|
2 |
|
|
2 |
|
|
|
|
|
|
|
2 |
|
|
|
|
2 |
|
|
|
||||
|
|
∞ |
|
|
3 x2 +1 |
|
|
|
|
|
|
|
∞ |
|
|
x5+1 |
|
|
|
|
|
|
|
|
|
|||||||||||
№ 41.7. |
∫ |
|
|
|
|
|
dx |
|
|
|
|
|
№ 41.7. |
∫ |
|
|
|
dx |
|
|
|
|
|
|||||||||||||
|
|
|
ex |
|
|
|
|
|
|
|
ex |
|
|
|
|
|
||||||||||||||||||||
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Выяснить сходимость интегралов от неограниченной функции.
|
1 |
|
|
sin |
|
x |
|
|
|
|
№ 41.8. |
∫ |
|
|
|
|
dx |
||||
|
ln(1+x) |
|||||||||
|
0 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
tg |
|
x |
|
|
|
|
№ 41.9. |
∫ |
|
|
|
|
|
dx |
|||
earcsin x −1 |
||||||||||
|
0 |
|
|
|
|
|
|
|
|
|
|
1 arctg |
x |
|
|
||||||
№ 41.10. |
∫ |
x2 −x |
|
|
dx |
|||||
|
0 |
|
|
|
|
|
|
|
|
|
№ 41.11. a) |
∫1 |
lnxxdx , b) |
||||||||
|
|
|
|
0 |
|
|
|
|
|
|
|
∞ arctg x |
|
|
|
|
|||||
№ 41.12. |
∫ |
3 x4 |
|
dx |
||||||
|
0 |
|
|
|
|
|
|
|
|
|
∫1 |
1 |
dx |
x ln x |
||
0 |
|
|
|
1 |
|
tg |
|
x |
|
|
|
|
|
|
|
|
№ 41.8. |
∫ |
|
|
|
dx |
|
|
|
|||||
arcsin x |
|
|
|
||||||||||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
arctg |
x |
|
|
|
|
|||||
№ 41.9. |
∫ |
|
|
dx |
|
|
|
||||||
|
esin x −1 |
|
|
|
|||||||||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
arcsin |
x |
|
|
|
|
|||||
№ 41.10. |
∫ |
dx |
|
|
|
||||||||
x3−x |
|
|
|
|
|
|
|
||||||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
ln x |
|
1 |
1 |
|
|||||
№ 41.11. a) ∫ |
|
∫ |
|
||||||||||
|
x3 |
dx , b) |
x3 ln x |
dx |
|||||||||
|
|
|
0 |
|
|
|
|
|
|
|
0 |
|
|
∞
№ 41.12. ∫arctg1x 3 x dx
0
Теория.
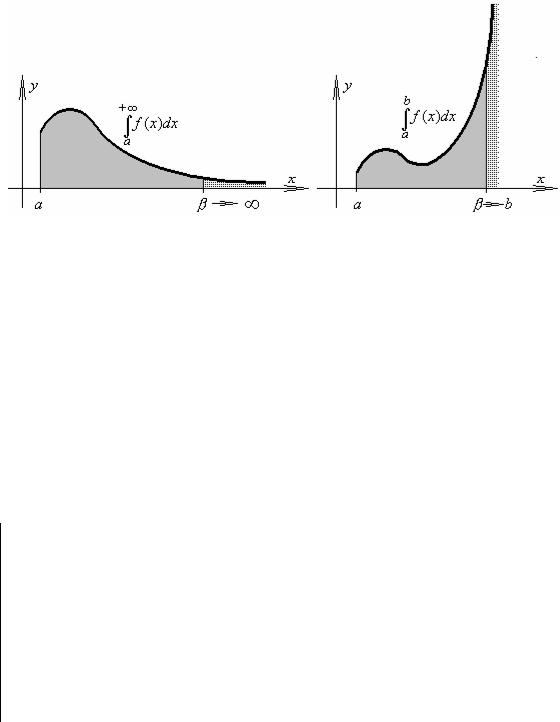
Несобственным интегралом по |
Несобственным интегралом от |
||
неограниченному промежутку называется: |
неограниченной функции называется: |
||
+∞ |
β |
b |
β |
∫ |
f (x)dx =βlim→+∞ ∫ f (x)dx |
∫ f (x)dx =βlim→b−0 |
∫ f (x)dx |
a |
a |
a |
a |
|
|
|
|
Обозначив через ω = +∞, b − 0 , удобно объединить оба случая
ω∫ f (x)dx = |
β |
βlim→ω ∫ f (x)dx. |
|
a |
a |
Если предел существует и конечен, несобственный интеграл называется сходящимся. Из формулы Ньютона-Лейбница
ω |
β |
|
|
β = lim |
(F(β) −F(a))=F(ω) −F(a) |
|
∫ |
f (x)dx = lim |
f (x)dx = lim F(x) |
|
|||
|
||||||
β→ω ∫ |
β→ω |
|
a |
β→ω |
|
|
a |
a |
|
|
|
|
|
вытекает, что сходимость несобственного интеграла равносильна сходимости первообразной, т.е. существованию конечного предела
lim F (x) =F (ω).
x→ω
В случае неотрицательной подынтегральной функции f (x) ≥ 0 имеются простые
признаки сходимости несобственных интегралов, позволяющие выяснить сходимость опосредовано (т.е. без нахождения первообразной).
Теорема. (Признак сравнения в общей форме). Пусть:
1) 0 ≤ f (x) ≤ g(x)
|
|
|
|
|
|
|
1) если “больший” интеграл |
ω∫g(x)dx <∞ |
“меньший” интеграл |
ω∫ f (x)dx <∞ |
|
|
(сходится) |
|
a |
|
a |
|
|
ω∫ f (x)dx =∞ |
|
ω∫g(x)dx =∞ |
|
|
если “меньший” |
интеграл |
“больший” интеграл |
||
|
(расходится) |
|
a |
|
a |
|
|
|
|
|
|
Теорема. (Признак сравнения в предельной форме). |
|
|
|||
|
Пусть: |
|
|
|
|
|
1) f (x) g(x) |
|
|
|
|
|
x→ω |
|
|
|
|
|
|
|
|
|
|
|
1) интегралы ω∫ f (x)dx , ω∫g(x)dx сходятся или расходятся одновременно. |
||||
|
a |
a |
|
|
|
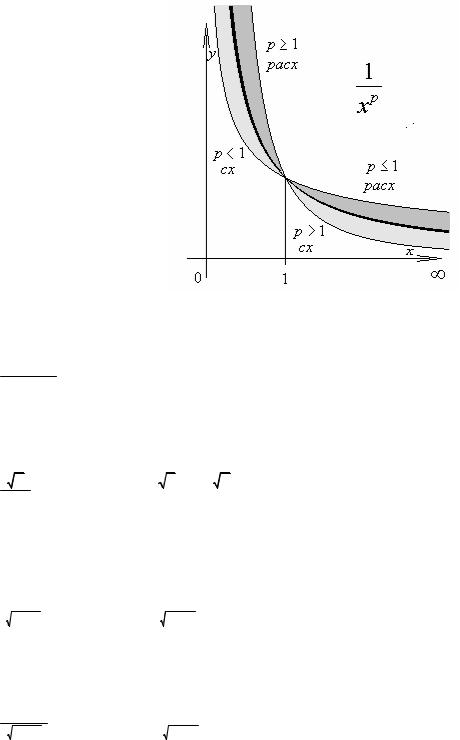
В качестве “эталонных” функций, с которыми чаще всего приходится сравнивать другие функции, отметим степенные:
∞ |
p ≤1, |
pacx |
|
1 |
|
|
p <1, |
cx |
|||
∫ |
1 |
dx = |
|
∫ |
1 |
dx = |
|||||
p >1, |
cx |
|
p ≥1, |
pacx |
|||||||
x p |
x p |
||||||||||
1 |
|
|
|
|
|
0 |
|
|
|
|
|
Решения.
№ 41.1.
∫∞ +x+1+ dx x3 2x 1
1
№ 41.2.
∫∞ x dx x2 −1
2
№ 41.3.
∫∞ arctg xdx
3 x2 +1
1
№ 41.4.
∫∞ arctg 1
3 x2 +1xdx
1
f (x) = |
|
x+1 |
|
x |
= |
1 |
p =2 >1 сходится. |
x3 |
|
|
x2 |
||||
|
+2x+1 x→∞ x3 |
|
|
||||
|
f (x) = |
|
x |
|
x |
= |
1 |
|
p = 3 |
>1 |
сходится. |
x2 |
|
|
3 |
||||||||
|
|
−1 x→∞ x2 |
|
2 |
|
|
|||||
|
|
|
|
|
|
|
x2 |
|
|
|
|
f (x) = arctg3 |
x |
|
π |
p = 2 |
|
|
|
2 |
<1 |
расходится. |
|||
|
2 |
|||||
x2 +1 |
x→∞ x3 |
3 |
|
|
||
|
|
arctg 1 |
|
1 |
|
1 |
|
p = 5 |
|
|
||
|
f (x) = |
|
|
x |
|
x |
= |
|
>1 |
сходится. |
||
3 |
x2 |
+1 |
2 |
5 |
||||||||
|
|
|
x→∞ x3 |
|
x3 |
|
3 |
|
|
|||
В следующих примерах демонстрируется применение признака сравнения для интегралов по неограниченному промежутку в общей форме. Полезно вспомнить, что:
lim |
ln x |
=0, |
lim |
xε |
=0 (ε >0) . |
|
|
||||
x→+∞ |
xε |
x→+∞ ex |
|
||
Отсюда, в частности, вытекает, |
что при достаточно больших значениях x [a,∞) имеют |
||||||||||||||||||
место оценки: |
|
|
|
|
|
|
|
|
xε |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
ln x |
≤const, |
|
|
≤const |
( ε > |
0). |
||||
|
|
|
|
|
|
|
|
|
|
ex |
|
||||||||
|
|
|
|
|
|
|
|
|
xε |
|
|
|
|
|
|
|
|
|
|
№ 41.5. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a) |
∫ |
ln xdx |
|
f (x) = ln x |
= ln x = ln x |
xε |
≤const |
|
1 |
=g(x) |
p = 4 −ε. |
||||||||
4 |
|
4 |
|||||||||||||||||
|
3 |
x4 |
|
|
3 |
x4 |
|
4 |
ε |
|
|
|
|
x |
|
3 |
|||
|
|
|
|
|
|
x3 |
x |
x3 |
|
|
|
|
3 −ε |
|
|||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Попробуем подобрать ε > 0 так, чтобы p = 4 |
−ε >1 (тогда интеграл от “большей” функции |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
g(x) |
будет сходящимся). Имеем 0 <ε < 1 . |
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
Следовательно, исходный интеграл сходится. |
|
|
|
||||||||||||||||
|
∞ |
ln x |
|
|
ln x |
|
ln2 |
|
|
|
|
|
|
|
|
|
|
||
b) ∫ |
|
g(x) = |
≥ |
= f (x) |
p =1. |
|
|
||||||||||||
|
x dx |
|
x |
x |
|
|
|||||||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Найдена “меньшая” функция f (x) , интеграл от которой расходится. |
|||||||||||||||||||
Следовательно, исходный интеграл расходится. |
|
|
|
||||||||||||||||
|
∞ |
ln x |
|
|
ln x |
|
ln2 |
|
|
|
|
1 |
|
|
|
||||
c) ∫ |
|
|
|
|
|
|
|
|
|
|
|||||||||
3 x dx |
|
g(x) = |
|
1 |
≥ |
1 |
= f (x) |
|
p = 3 |
<1. |
|
||||||||
|
2 |
|
|
|
|
x3 |
|
x3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Найдена “меньшая” функция f (x) , интеграл от которой расходится. Следовательно, исходный интеграл расходится.
№ 41.6.
|
∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a) |
∫2 |
|
1 |
|
dx |
f (x) = |
|
|
1 |
|
≤ |
1 |
|
= g(x) p = 4 >1. |
|
|
|
|
||||||||
|
|
3 |
|
|
|
4 |
|
|
|
|
|
|
||||||||||||||
|
|
3 x4 ln x |
|
|
|
|
x4 ln x |
|
|
|
|
|
|
|
|
3 |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
x3 ln2 |
|
|
|
|
|
|
|
||||||||||
Найдена “большая” функция g(x) , интеграл от которой сходится. |
|
|
|
|||||||||||||||||||||||
Следовательно, исходный интеграл сходится. |
|
|
|
|
|
|
||||||||||||||||||||
|
∞ |
1 |
|
|
|
|
|
|
|
1 |
|
|
|
xε |
1 |
1 |
1 |
|
|
|
1 |
|
||||
c) ∫ |
dx |
|
g(x) = |
|
|
|
|
|
|
= f (x) |
|
p = |
+ε . |
|||||||||||||
3 x ln x |
|
3 x |
ln x |
|
= |
ln x |
|
3 x xε |
|
≥ const |
1+ε |
|
3 |
|||||||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p = 1 +ε ≤1 |
|
|
|
|
|
|||
Попробуем |
подобрать ε > 0 |
так, |
чтобы |
(тогда |
интеграл |
от “меньшей” |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
функции f (x) |
будет расходящимся). Имеем 0 <ε ≤ 2 . |
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
Следовательно, исходный интеграл расходится.
∞
|
1 |
|
|
|
|
b) ∫xln xdx |
|
|
|
||
2 |
|
|
|
|
|
Имеем: |
|
|
|
|
|
f (x) = |
1 |
≤ |
1 |
= g(x) |
p =1. |
|
xln x |
|
xln2 |
|
|
Найдена “большая” функция g(x) , интеграл от которой расходится, что бесполезно. По другому:
g(x) = |
1 |
= |
xε |
|
1 |
≥ |
1 |
1 |
= f (x) |
p =1+ε >1. |
xln x |
ln x x xε |
|
||||||||
|
|
|
const x1+ε |
|
|
|||||
Теперь найдена “меньшая” функция f (x) , интеграл от которой сходится, что также
бесполезно.
Попробуем найти интеграл “непосредственно”:
∞ |
|
|
|
|
|
|
|
|
∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
1 |
dx = |
|
|
1 |
|
d ln x =ln ln x |
|
|
= lim ln ln x −ln ln 2 =∞. |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
∫xln x |
∫ln x |
|
|
2 |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x→∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
2 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Следовательно, исходный интеграл расходится. |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
№ 41.7. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
∞ |
3 x2 +1 |
|
|
|
|
|
|
|
|
|
|
|
|
3 x2 +1 |
|
|
|
|
|
3 x2 |
|
xε |
2 |
|
|
|
|
|
|
1 |
|
|
|
|
2 |
|
|||||||||||||||||
∫ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x3 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
dx |
|
|
|
f |
(x) = |
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
≤const |
|
|
|
|
, |
p =ε − |
|
. |
|||||||||||||||
e |
x |
|
|
|
|
|
|
|
e |
x |
|
|
e |
x |
e |
x |
ε |
|
|
|
2 |
|
3 |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x→∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
xε−3 |
|
|
|
|
|
||||||||||||||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
Попробуем подобрать ε > 0 так, чтобы p =ε − |
>1 (тогда интеграл от “большей” функции |
||||||||||||||||||||||||||||||||||||||||||||||||||||
будет сходящимся). Имеем ε > 5 |
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
. Следовательно, исходный интеграл сходится. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
№ 41.8. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
1 |
|
sin |
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
∫ |
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
ln(1+x) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a = 0 |
|
|
Подынтегральная |
функция |
|
имеет |
особенность |
на |
конце |
интервала [a,b] =[0,1] . |
||||||||||||||||||||||||||||||||||||||||||||||
Имеем: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
f |
(x) = |
sin |
|
x |
|
|
x |
= |
1 |
= g(x), |
|
p = 1 <1 |
|
|
|
сходится. |
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
1 |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
ln(1+x) x→0 |
x |
|
|
|
x2 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
№ 41.10. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
arctg |
|
|
|
x |
|
|
2 |
arctg |
x |
|
|
|
arctg |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
∫ |
x2 −x |
|
|
dx |
=∫ |
|
x2 −x |
|
|
|
dx |
+∫ |
|
|
|
x2 −x |
dx. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
0 |
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a = 0 и b =1 интервала |
|
Подынтегральная функция имеет особенности на обоих концах |
|||||||||||||||||||||||||||||||||||||||||||||||||||||
[a,b] =[0,1] . Разобьем интеграл в сумму двух и исследуем каждый отдельно. Имеем: |
|||||||||||||||||||||||||||||||||||||||||||||||||||||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
arctg |
|
|
|
x dx |
|
|
|
f (x) = arctg x |
|
|
|
|
x |
|
=− |
1 |
|
, |
p = 1 |
<1 |
|
сходится. |
|||||||||||||||||||||||||||||
∫ |
x2 −x |
|
|
|
|
−x |
|
1 |
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 −x |
|
x→0 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
||||||||||||||||||
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
arctg |
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
arctg |
|
|
x |
|
arctg |
|
x |
|
|
arctg 1 |
|
π |
|
|
|
|
|||||||||||||||||
∫ |
|
|
|
dx |
|
|
|
|
|
f (x) = |
|
|
|
|
|
|
|
|
4 |
|
p =1 |
|
|||||||||||||||||||||||||||||||
x2 −x |
|
|
|
|
|
|
x2 −x |
= |
x(x−1) |
x→1 1(x−1) |
|
= |
|
, |
расходится. |
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
(x−1) |
|||||||||||||||||||||||||||||||||||||||||||||||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Следовательно, исходный интеграл расходится.
В следующих примерах демонстрируется применение признака сравнения для интегралов от неограниченной функции в общей форме. Отметим, что:
|
|
|
|
|
|
lim xε ln x = |
x = |
1 |
|
1 |
= y →+∞ |
= lim |
1 |
|
ln |
|
1 |
|
= lim |
−ln y = |
0 |
(ε >0) . |
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
x→+0 |
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y→+∞ yε |
|
|
|
|
y→+∞ |
yε |
|
|
||||||||||||||||||
Отсюда, в частности, |
|
вытекает, |
|
|
что при достаточно малых значениях |
x (0, a] имеет |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
место оценка: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
№ 41.11. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
xε |
|
ln x |
|
|
|
≤const |
|
(ε >0) |
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ln x |
|
|
|
|
|
|
|
ln x |
|
|
xε |
|
ln x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
a) |
∫ |
ln xdx |
|
|
f (x) |
|
= |
|
|
= |
|
|
= |
|
|
≤const |
|
1 |
|
|
=g(x) |
p = 1 |
+ε. |
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
1 |
|
|
|
1 |
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
x2 |
|
|
x2+ε |
|
|
|
|
|
|
|
x2 +ε |
|
|
|
|
|
2 |
|
||||||||||||||||
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Попробуем подобрать |
ε > 0 так, чтобы p = |
1 +ε <1 (тогда интеграл от “большей” функции |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 . |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
g(x) будет сходящимся). Имеем 0 <ε < |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Следовательно, исходный интеграл сходится. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
b) ∫1 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
dx +∫1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
1 |
dx =∫2 |
|
1 |
|
|
|
|
|
|
1 |
dx. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
x ln x |
|
x ln x |
|
|
|
x ln x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
0 |
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a = 0 и b =1 интервала |
||||||
Подынтегральная функция имеет особенности на обоих концах |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[a,b] =[0,1] . Разобьем интеграл в сумму двух и исследуем каждый отдельно. Имеем: |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
p = 1 <1 |
|
|
|
||||||
|
|
|
|
dx |
|
|
|
f (x) |
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
≤ |
|
|
|
|
|
|
= |
|
|
=g(x), |
|
|
|
|
сходится. |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
∫ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
x ln x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
ln x |
|
|
|
|
|
|
|
|
|
ln 1 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
x2 ln2 |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
1 |
|
|
|
|
||||||||
|
|
|
|
|
dx |
f (x) = |
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
, |
p =1 |
расходится. |
||||||||||||||||||||||||||
∫1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1(x |
−1) |
(x −1) |
||||||||||||||||||||||||||||||||
x ln x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x ln x |
|
|
|
|
|
|
|
|
x ln((x−1)+1) x→1 |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Следовательно, исходный интеграл расходится. |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
№ 41.12. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
∞ arctg x |
|
1 |
arctg x |
|
|
|
|
|
|
|
∞ arctg x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
∫ |
3 x4 |
|
|
dx =∫ |
3 x4 |
dx +∫ |
|
|
3 x4 |
|
|
|
dx. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
0 |
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Разбив интеграл в сумму двух, исследуем каждый отдельно. Имеем:
1 |
arctg xdx |
f (x) = arctg x |
|
x |
= |
1 |
|
, |
p =1 |
<1 |
сходится. |
||||||
∫ |
4 |
1 |
|
||||||||||||||
3 x4 |
3 x4 |
x→+0 x3 |
|
|
x3 |
|
|
3 |
|
|
|||||||
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∞ |
arctg xdx |
f (x) =arctg x |
|
|
π |
|
|
|
|
|
|
|
|
||||
∫ |
|
|
2 |
|
, p |
= 4 |
>1 |
|
сходится. |
||||||||
|
4 |
|
|||||||||||||||
3 |
x |
4 |
3 |
x |
4 |
x→+∞ |
|
|
|
3 |
|
|
|
||||
1 |
|
|
|
|
|
|
x3 |
|
|
|
|
|
|
|
|
||
Следовательно, исходный интеграл сходится.
