Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Харьковский Национальный Университет им. В. Н. Каразина

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

матан

.pdf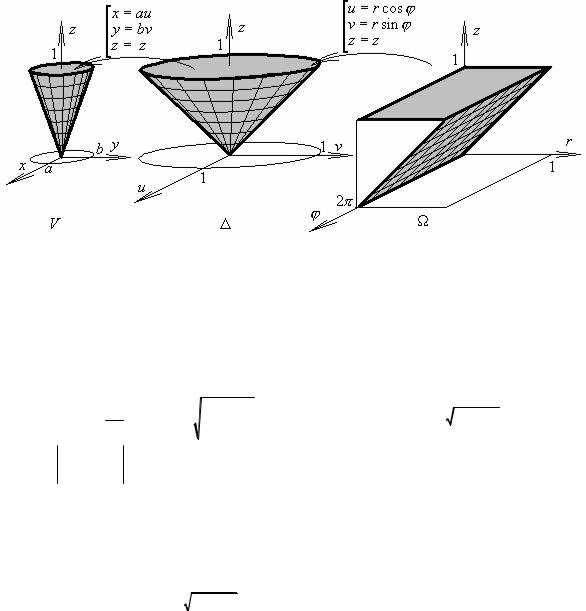

Скачиваний:

Добавлен:

23.02.2015

Размер:

1.44 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 67 / 147 8 9 10 11 12 13 14 > Следующая >>>

№ 35.6.

V =∫∫∫1 dxdydz =→

Перейдем от старых координат (x, y, z) к промежуточным (u,v, z) , полагая что:

x =au

dxdydz =

D(x, y, z)

dudvdz =

xu′

xv′ xz′

dudvdz =

a 0 0

dudvdz =ab dudvdz

y =bv

y′

0 b 0

z = z

D(u, v, z)

zu′

zv′ zz′

0 0 1

V ={ax22

→=∫∫∫ D(x, y, z) D(u, v, z)

∆

+	y2	≤1,	x2	+	y2	≤ z ≤1} → ∆={u2 +v2 ≤1, u2 +v2 ≤ z ≤1}.
	b2		a2		b2

dudvdz =∫∫∫ab dudvdz =→

∆

Переходя далее от промежуточных координат (u,v, z) к цилиндрическим (r,ϕ, z)

u =r cosϕ

v =r sinϕ dudvdz =r drdϕdz

z = z

∆={u2 +v2 ≤1, u2 +v2 ≤ z ≤1} → Ω={0 ≤ϕ ≤2π, 0 ≤r ≤1, r ≤ z ≤1},

находим:

	2π	1	1	1
→=ab∫∫∫rdrdϕdz=ab ∫(		∫(	∫rdz )dr	)dϕ=2πab∫r (1−r )dr =2πab(12 r2 −13 r3 )	1	=13πab.
					1
					0
Ω	0	0	r	0

Получена известная формула объема конуса V = 13πab , в основании которого лежит эллипс с площадью SOCH =πab и высотой h =1.

Замечание. Координаты (r,ϕ, z) для исходных декартовых координат (x, y, z) получили название обобщенных цилиндрических координат:

x =ar cosϕ	D(x, y, z)	=ab r
x =ar cosϕ
y =br sinϕ
z = z	D(r,ϕ, z)

36. Тройные интегралы. Переход к сферическим координатам

Условия.

№ 36.1. Найти массу тела, ограниченного заданными поверхностями, с объемной плотностью ρ = ρ(x, y, z) .

x2 + y2 + z2 =a2 , ρ = x2 + y2 + z2 .	x2 + y2 + z2 =a2 , ρ =		1	.
		x2	+ y2 + z2

№ 36.2. Найти заряд тела, ограниченного заданными поверхностями, с объемной плотностью ρ = ρ(x, y, z) .

x	2	+ y	2	+ z	2	=2az,	ρ =	1	x2 + y2 + z2 =az, ρ = x2 + y2 + z2 .
								x2 + y2 + z2 .

№ 36.3. Найти центр масс тела, ограниченного заданными поверхностями, с объемной плотностью ρ = ρ(x, y, z) .

x2 + y2 + z2 =az, z ≥ x2 + y2 ;				x2 + y2 + z2 =a2 , z ≤ x2 + y2 ;
ρ =		1	.	ρ = x2 + y2 + z2 .
	x2	+ y2 + z2

Найти объем тела, ограниченного поверхностями.

№ 36.4.

x2 + y2 + z2 =a2 ,

z ≥

x2 + y2

;

№ 36.4.

x2 + y2 + z2 =az,

z ≥

3(x2 + y2 );

№ 36.5.

=1.

№ 36.5.

=1,

≥

Теория.

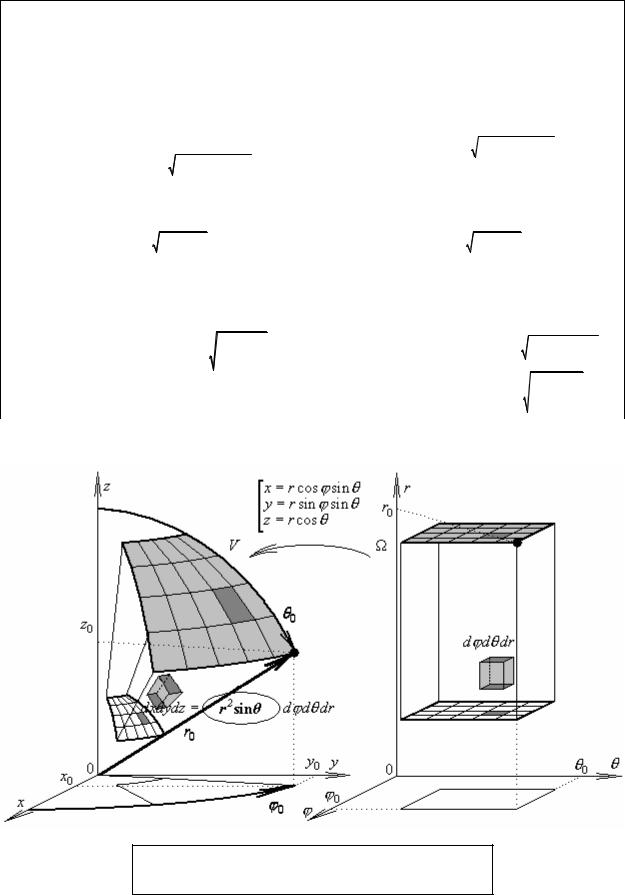
∫∫∫f (x2 + y2 + z2 )dxdydz =∫∫∫f (r2 ) r 2sinи dϕdθdr

V Ω

Решения.

№ 36.1.

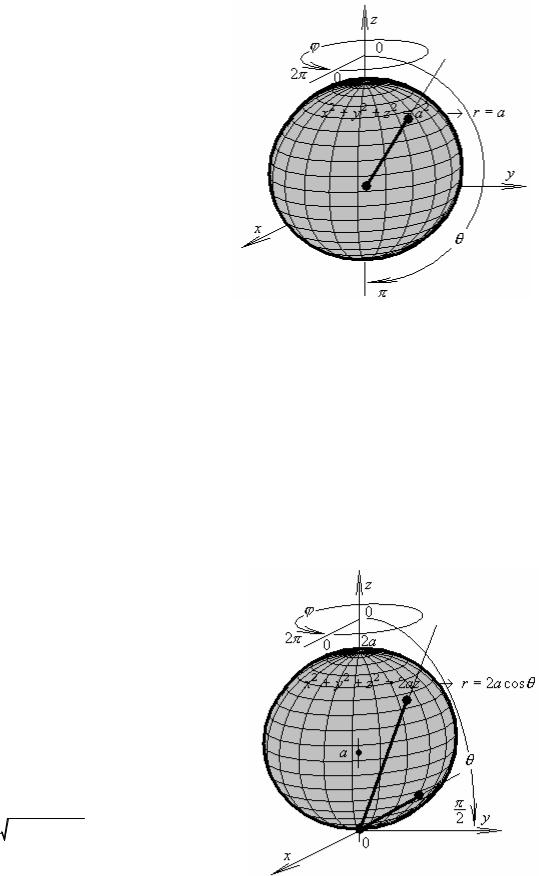
Сфера

S ={x2 + y2 + z2 =a2 }

ограничивает шар

V ={x2 + y2 + z2 ≤a2 }

радиуса a с центром в начале координат (0,0,0) :

m =∫∫∫ρ (x, y, z)dxdydz =

=∫∫∫(x2 + y2 + z2 ) dxdydz =→

Учитывая вид подынтегральной функции f (x2 + y2 + z2 ) и “сферическую” форму объема

V , перейдем к сферическим координатам. Поскольку

то

x2 + y2 + z2 =a2

→ r2 =a2 r =a ,

V ={x2 + y2 + z2 ≤a2 } → Ω={0 ≤ϕ ≤2π, 0 ≤θ ≤π, 0 ≤r ≤a}.

Имеем:

→=∫∫∫r

2π

sinθ dr )dθ

2π

sinθ dϕdθdr = ∫

∫(

∫r

dϕ = ∫

1 dϕ ∫sinθdθ ∫r

dr =

Ω

=2π (−cosθ)

1 r5

= 4 πa5 .

№ 36.2.

“Смещенная” сфера

S ={x2 + y2 + z2 =2az}

ограничивает шар

V ={x2 + y2 +(z −a)2 ≤a2 }

радиуса a с центром в точке (0,0, a) :

q =∫∫∫ρ (x, y, z)dxdydz =

=∫∫∫

dxdydz =→

y2 + z2

Учитывая вид подынтегральной функции f (x2 + y2 + z2 ) и “сферическую” форму объема V , перейдем к сферическим координатам.

Поскольку

то

x2 + y2 +z2 =2az

→ r2 =2ar cosθ

r =2a cosθ ,

V ={x2 + y2 +(z −a)2 ≤a2 } → Ω={0 ≤ϕ ≤2π, 0 ≤θ ≤

, 0 ≤r ≤

Имеем:

2∫π (

2a ∫cosθ rsinθdr

)dϕ=

2∫π

→=∫∫∫

r2sinθ dϕdθdr =

∫2 (

)dθ

1 dϕ ∫2 (

Ω

π2

=2π 2

∫sinθ r

2a cosθ

dθ =4a

π ∫sinθ cos θdθ =−4a π ∫cos θd cosθ =

=−4a

dt =4a

dt =3 a π.

π ∫t

2a cosθ}.

sinθ	2a ∫cosθ rdr )dθ =
	0

№ 36.3.

Из физических понятий очевидно, что центр масс однородного тела с круговой симметрией находится на его оси: (x0 , y0 , z0 )=(0,0,?). Цель приведенных ниже расчетов,

в частности, показать адекватность математических формул интуитивным представлениям.

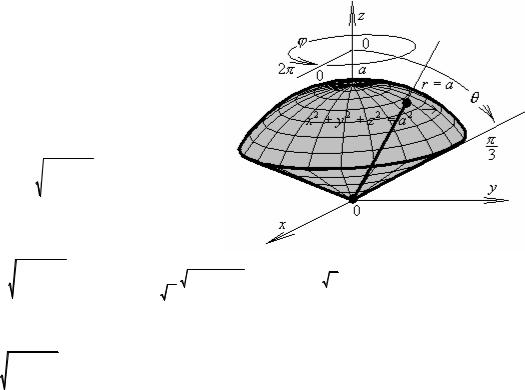
Объем V ограничен верхней половиной “смещенной” сферы

x2 + y2 +(z − a2 )2 =(a2 )2

радиуса a2 с центром в точке (0, 0, a2 )и конусом z = x2 + y2 :

Найдем массу тела:

m =∫∫∫ρ(x, y, z)dxdydz =

=∫∫∫x2 + y12 + z2 dxdydz =→

Учитывая вид подынтегральной функции f (x2 + y2 + z2 ) и “сферическую” форму объема

V (Сравнить с № 35.5), перейдем к сферическим координатам. Поскольку

z = x2 + y2	→ r cosθ = r2 sin2 θ	tgθ =1 θ =π	,
		4
x2 + y	2 + z2 =az → r2 =ra cosθ	r =a cosθ,

то

+(z −

V ={z ≥

+ y

2 )

≤(2 )

} → Ω={0

≤ϕ ≤2π,

0 ≤θ ≤

, 0 ≤r ≤a cosθ}.

Имеем:

2π

a cosθ

→=∫∫∫

r2sinθ dϕdθdr = ∫

∫(

∫

sinθ

)dθ

dϕ =2π ∫(

sinθ

∫

1 dr

)dθ =

Ω

=−πa (cos

=2πa∫sinθ cosθdθ =−2πa∫cosθd cosθ =−2πa

2 π

−cos

πa

2 cos θ

= 2 .

Далее найдем

координаты центра масс, учитывая симметрию тела относительно

координатных

плоскостей

xOz,

yOz

нечетность

подынтегральных

функций

относительно переменных x,

y :

+ z2 dxdydz =0,

= m ∫∫∫xρ (x, y, z)dxdydz = m ∫∫∫x x2 + y2

+ z2 dxdydz =0.

= m ∫∫∫yρ (x, y, z)dxdydz = m ∫∫∫y x2 + y2

= m ∫∫∫zρ

(x, y, z)dxdydz = m ∫∫∫z x2

+ y2

+ z2

dxdydz = m ∫∫∫r cosθ r2

Ω

2π

a cosθ

2π

a cosθ

(

)dθ

( cosθ sinθ

m ∫

∫

r cosθ sinθ dr

dϕ =

r dr

r2sinθ dϕdθdr =

)dθ =

a cosθ

= 2mπ 12 ∫cosθ sinθ

dθ =

πma

∫cos3 θ sinθ

dθ =−πma

∫cos3 θ dcosθ =

πa2

4 π

πa2

3πa2

=− 4m cos

0 =− 4m

(cos

−cos

0)=− 4m

(

−1)= 16m

№ 36.4.

V =∫∫∫1 dxdydz =→

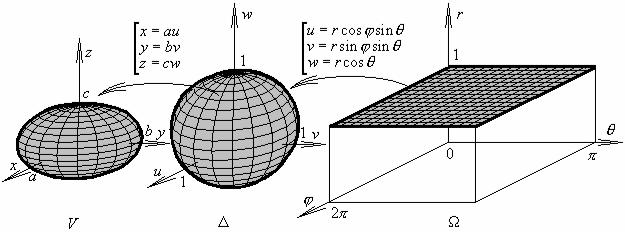
Объем V ограничен верхней частью сферы

радиуса a

x2 + y2 + z2 =a2

центром

начале

координат

(0,0,0) и конусом

+ y2

z =

Учитывая “сферическую” форму объема V ,

перейдем к сферическим координатам.

Поскольку

z =

x2 + y2

→ r cosθ =

r2 sin2 θ

tgθ = 3

θ =π ,

x2 + y2 + z2 =a2 → r2 =a2 r =a,

то

V ={z ≥

x2 + y2

, x2 + y2 + z2 ≤a2 } → Ω={0 ≤ϕ ≤2π, 0 ≤θ ≤π

, 0 ≤r ≤a}.

Имеем:

2π

∫∫∫

(

sinθ dr )dθ

→=

r sinθ dϕdθdr =

∫

sinθdθ

∫

r dr =

dϕ =2π

Ω

2π (−cosθ)

π3

1 r3

2π 1

1 a3

=π a3.

№ 36.5.

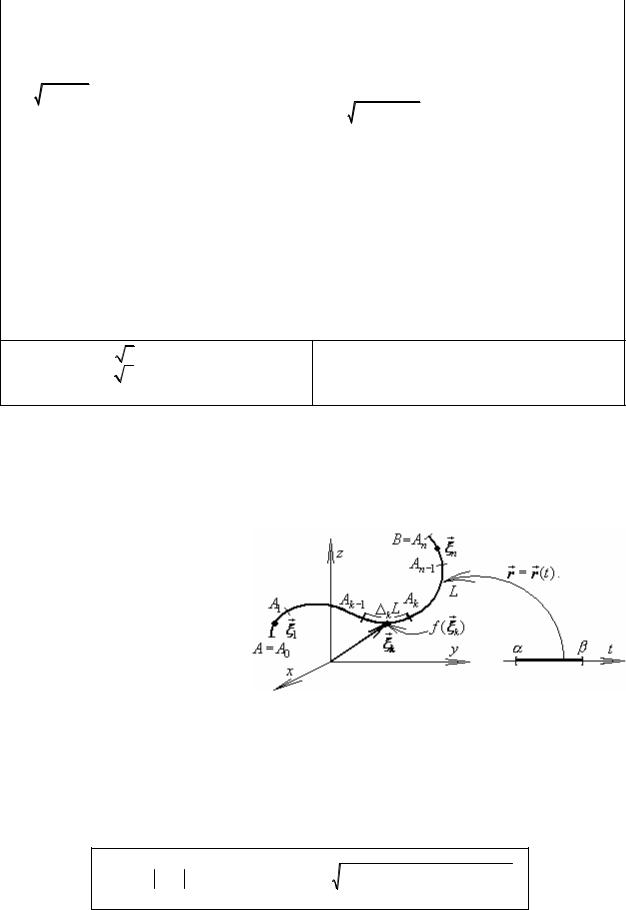
V =∫∫∫1 dxdydz =→

Перейдем от старых координат (x, y, z) к промежуточным (u,v, w) , полагая что:

x =au

D(x, y, z)

xu′ xv′ xw′

a 0 0

dudvdw=abc dudvdw

y =bv

dxdydz =

dudvdw=

y′

dudvdw=

b 0

z =cw

D(u, v, w)

zu′ zv′ zw′

0 0 c

V ={

≤1}→∆={u2 +v2 +w2 ≤1}.

D(x, y, z)

→=∫∫∫

dudvdw=∫∫∫abc dudvdw=→

D(u, v, w)

∆

Переходя далее от промежуточных координат (u,v, w) к сферическим (r,θ,ϕ)

u =r cosϕ sinθ

dudvdw=r 2sinи dϕdθdr ∆→Ω={0 ≤ϕ ≤2π, 0≤θ ≤π,

0≤r ≤1},

v =r sinϕ sinθ

w=r cosθ

находим:

2π

∫∫∫

(

)dθ

→=abc

sinθ

dϕdθdr =abc

∫

r sinθ dr

=2πabc

∫

sinθdθ

∫

dr =

dϕ

Ω

=2πabc 2 13 = 43 πabc.

Получена полезная формула объема эллипсоида V = 43 πabc . В частности, объем шара

радиуса R = a = b = c равен V = 4 π R3 .
	3
Замечание. Координаты (r,θ,ϕ)		для исходных декартовых координат (x, y, z) получили
название обобщенных сферических координат
x =ar cosϕ sinθ	D(x, y, z)		=abc r 2sinи
x =ar cosϕ sinθ
y =br sinϕ sinθ
y =br sinϕ sinθ	D(r,θ,ϕ)
z =cr cosθ	D(r,θ,ϕ)

37. Криволинейные интегралы по длине (масса, заряд)

Условия.

№ 37.1.

Найти массу кривой L с линейной плотностью ρ = ρ(x, y, z) :

x = cost

L =

= ch t

L =

y = sin t , t [0,2π]

= sh t , t

[0,1] ,

z = t

= t

ρ = x

+ y

ρ =

1+ x2 + y2

№ 37.2.

Найти заряд кривой L с линейной

плотностью заряда ρ = ρ(x, y, z) :

x = e−t cost

x = cos e−t

L =

y = sin e−t

, t [0, +∞)

L =

y = e−t sin t , t [0,+∞) ,

= e−t

z = e−t

ρ = xyz

№ 37.3. Найти центр масс однородной кривойL :

x = cost

x = e−t cost

L =

y = sin t , t [0,2π]

y = e−t sin t , t [0,+∞)

L =

z = t

−t

z = e

№ 37.4.

Найти длину кривойL :

	x = t cos	2t
	y = t sin	2t , t [0,1]	,
L =

	z = t

	x = t cost −sin t	,
L =	y = t sin t + cost , t [0,1]	,
	z = t

Теория.

Пусть дана простая гладкая кривая

	x =x(t)
L ={r =r (t), t [α, β]}=	y = y(t), t [α, β]
	z =z(t)

(	′	′
(	непрерывная r (t) , причем	r (t) ≠ 0) ,

на которой распределена масса (заряд) с заданной линейной непрерывной плотностью

ρ = f (r ) = f (x, y, z) .

Найдем массу (заряд) кривой. Разобьем кривую L на малые части Lk длины ∆k L и выберем

на них промежуточные точки ξk . Тогда масса m (заряд q ) равна:

n		n
m =∑	∆k m = lim	∑
k =1	d →0	k =1
k =1		k =1

f (ξk )∆k L = lim ∑ f (ξk ,ηk ,ζk )∆k L .

d →0 k =1

Полученный предел называется криволинейным интегралом по длине от функции f (r ) по кривой L и обозначается:

∫f (r )dL =∫f (x, y, z)dL .

L L

Он может быть сведен к следующему определенному:

ββ

∫f (r (t)) r′(t) dt =∫f (x(t), y(t), z(t)) (xt′(t))2 +(yt′(t))2 +(zt′(t))2 dt .

αα

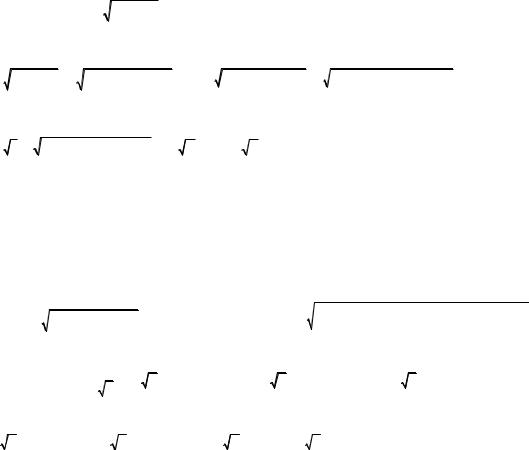
Решения.

№ 37.1.

m =∫ρ(x, y, z)dL =∫

x2 + y2

z dL =[x =cos t,

y =sin t,

z =t;

0 ≤t ≤2π ]=

2∫π

x2 + y2

x′2 + y′2 + z′2 dt =

2∫π

cos2 t +sin2 t

cos′2 t +sin′2 t +t′2 dt =

2π

(2π )2

= ∫

1 t

t +cos

dt =

2 ∫tdt = 2

sin

2 .

№ 37.2.

−t

cos t,

y =e

−t

sin t, z =e

−t

;

q =∫ρ(x, y, z)dL =∫x y z dL = x

0 ≤t <+∞

=+∞∫x y z

x′2 + y′2 + z′2 dt =+∞∫e−t

cos t e−t

sin t e−t

(e−t cos t )′2 +(e−t sin t )′2 +(e−t )′2 dt =

+∞

(

)

+∞

= ∫e

−4t

cos t

sin t

3dt =

∫e

−4t

sin 2t dt =

Im ∫e

(−4+i2)t

dt =

−4+i2 t

Im −4 +i2

=−

−4 −i2

=−

−2

−4 +i2

42 +22

2 42 +22

№ 37.3.

При

нахождении

центра

масс

неоднородной кривой

линейной

плотностью

ρ =ρ(r ) =ρ(x, y, z)

и массой

m =∫ρ(r )dL =∫ρ(x, y, z)dL

воспользуемся определением центра масс системы материальных точек. Разобьем

кривую L точками на малые части Lk ,

с массами

∆k m ≈ ρ(ξk )∆k L = ρ(ξk ,ηk ,ζk )∆k L ,

настолько малые,

что

каждую можно

рассматривать как материальную точку

ξk =(ξk ,ηk ,ζk ) . Тогда:

∫xρ(x, y, z)dL

∫r

∫yρ(x, y, z)dL

r0 ≈

∑ξk ∆k m ≈

∑ξk

ρ(ξk )∆k L d→→0

ρ(r )dL

k =1

∫zρ(x, y, z)dL

Из физических соображений очевидно, что центр масс однородной винтовой линии находится на ее оси: (x0 , y0 , z0 ) = (0,0,π ). Цель приведенных ниже расчетов, в частности,

убедиться в адекватности математических формул интуитивным представлениям. Найдем массу кривой

m =∫ρ(x, y, z)dL =∫ρ dL =

=[x =cos t, y =sin t, z =t;

0≤t ≤2π ]=

=ρ

2∫π

x′2 + y′2 + z′2 dt = ρ

2∫π

cos′2 t +sin′2 t +t′2 dt =

=ρ

2∫π

sin2 t +cos2 t +12 dt = ρ

2∫π

2dt =2

2πρ.

Далее найдем координаты центра масс:

2∫π cos t

x0 =

∫xρ (x, y, z)dL =

∫xρdL =

∫xdL =

2dt =0,

y0 =

∫yρ (x, y, z)dL =

∫yρdL =

∫ydL =

2∫π sin t

2dt =0,

2π

ρ (2π )2

z0 =

∫zρ (x, y, z)dL =

∫zρdL =

∫zdL =

∫t 2dt = 2

=π.

№ 37.4.

2t,

y =t sin

2t, z =t;

x′

+ y′

+ z

′

dt =

L =∫1 dL = x =t cos

0 ≤t ≤1 =∫

=∫1

(t cos 2t )′2 +(t sin

2t )′2 +t′2 dt = 2 ∫1

1+t2 dt =→

Воспользовавшись ранее найденным интегралом (см. № 23.3.)

L =α∫ 1+ϕ2 dϕ = 12 (ln (α+ 1+α2 )+α 1+α2 ),

получим

→= 1

(ln (1+ 1+12 )

+1 1+12 )= 1

(ln (1+ 2 )+

2 ).

38. Криволинейные интегралы по координатам (работа силы)

Условия.

№ 38 1.	Найти работу силы F при перемещении материальной точки из начала A в
конец B кривой LAB .
LAB =	x = ch t			y		x = cost			z
LAB =	y = sh t , t [−1,	+1]	,	F = z	LAB =	y	= sin t , t [−π, +π]		, F = x
	z = t			x		z	= t		y

№ 38 2.	Найти работу силы FTP			трения	№ 38.2.	Найти работу силы FC
при перемещении материальной точки по					сопротивления воздуха при перемещении
плоской кривой					материальной точки по кривой
LAB =	x = x(t)	β]				x = x(t)
LAB =	y = y(t), t [α,	β]			LAB =	y	= y(t), t [α, β]
						z	= z(t)

№ 38.3.	Найти работу силы FT			тяготения,	№ 38.3.	Найти работу силы Fy
создаваемой материальной точкой массой					упругости, создаваемой бесконечно
M , находящейся в начале координат, при					растяжимой пружиной прикрепленной к
перемещении материальной точки массой					началу координат, при перемещении
m по кривой					материальной точки по кривой
LAB =	x = x(t)	β]				x = x(t)
LAB =	y = y(t), t [α,	β]			LAB =	y	= y(t), t [α, β]
	z = z(t)					z = z(t)
						z = z(t)

№ 38.4.	Найти работу векторного поля F (r ) = grad u(r )						при перемещении
материальной точки из начала A конец B кривой LAB .
LAB =	x = x(t)	β]				x = x(t)			A = B
LAB =	y = y(t), t [α,	β]			LAB =	y	= y(t), t [α, β]	,	A = B
	z = z(t)					z	= z(t)

Теория.

Пусть дана простая гладкая кривая

	x =x(t)
L ={r =r (t), t [α, β]}=	y = y(t), t [α, β]
	z =z(t)

	( непрерывная r′(t) , причем r′(t) ≠0) ,

воспринимаемая, как траектория движения материальной точки. Тогда для любых двух точек A1(r (t1)) и A2 (r (t2 )) можно сказать, что одна из них A1 встретится раньше

другой A2 , понимая под этим, что t1 < t2 . Таким образом, конкретная параметризация

автоматически задает направление движения вдоль кривой или, как говорят, ориентацию. В частном случае, когда кривая простая (без точек самопересечения), направление движения однозначно определяется указанием одной из концевых точек A или B в качестве начала или конца. Поэтому простые кривые с заданной ориентацией обозначаются LAB (или LBA ). Если дополнительно кривая гладкая, то направление

движения можно определить, задав непрерывное поле единичных векторов касательных

ф(r ) =τ (r (t)) = rr′′((tt)) (или −τ (r ) ).

<<< < Предыдущая 1 2 3 4 5 67 / 147 8 9 10 11 12 13 14 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
23.02.201534.74 Кб11маркетинг (робота с Ирой).docx
#
12.11.2019365.57 Кб9маркетинг услугТ 1-4.doc
#
23.02.201539.71 Кб5Маркетинг.docx
#
01.05.2019275.97 Кб3Маркетингова географія Л.1.doc
#
23.02.2015173.28 Кб16мат.методы.docx
#
23.02.20151.44 Mб69матан.pdf
#
23.02.20152.78 Mб86Матем. анализ. Методичка(1 семестр).doc
#
13.03.20161.44 Mб37Матеріали до словника 2.doc
#
13.03.2016105.98 Кб4материаловедение Лекция 1.doc
#
25.08.201938.33 Кб4Материалы 3_1.docx
#
10.11.2019241.66 Кб1материалы для лекции 1.doc