Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Харьковский Национальный Университет им. В. Н. Каразина

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

матан

.pdf

Скачиваний:

Добавлен:

23.02.2015

Размер:

1.44 Mб

Скачать

☆

<<< < Предыдущая 1 2 34 / 144 5 6 7 8 9 10 11 12 13 14 > Следующая >>>

Найдем вектор скорости.

a cos t

−a sin t

2 a

r (t) = a sin t

v (t) =r ′(t) = a cos t

t = 1

	−	3	a
		2
=		1 a
		2
		1
		1

−

2 1+ a

v(t)

r′(t)

= (−a sin t )

+(a cos t )

+12

= 1+a2 ,

τ =

v(t)

2 1+ a2

1+ a

Вектор скорости v(t) =rt′(t) направлен по касательной к траектории движения и может

служить в качестве направляющего вектора касательной прямой. Уравнения касательной прямой:

a) параметрические

	1		3	1
x =	2 a −			a (t − 3 π )
x =	2 a −		2	a (t − 3 π )
	3	a + 12 a (t − 13 π ) ,
r =r (t0 ) +rt′(t0 )(t −t0 ) y =	3
r =r (t0 ) +rt′(t0 )(t −t0 ) y =	2

	1 π +1 (t − 1 π )
z =	1 π +1 (t − 1 π )
	3			3

b) канонические

− 1 a

y −

z −

1 π

r −r (t

) ↑↑r′(t

)

−

12 a

Уравнение нормальной плоскости:

(r −r (t0 ), rt′(t0 ))=0 − 23 a (x − 12 a)+ 12 a (y −

−∞<t <+∞;

23 a)+1 (z −13 π )=0

№ 31.2.

На уравнения двух поверхностей, задающих кривую, как линию их пересечения, можно смотреть как на систему двух уравнений с тремя неизвестными (x, y, z) :

x2 + y2 = z

4 −2x −4 y = z

Выражая “мысленно” какие либо две переменные (например, (x, y) ) через третью z , выступающую в роли свободного

параметра t = z , приходим к параметрическим уравнениям кривой:

x = x(z)

y = y(z)

z = z

Найдем направляющий вектор касательной прямой в заданной точке (x0 , y0 , z0 ) =(2, −2, +8) .

x′z		x′z
y′z		= y′z
z	′	1
	z

Для этого необходимо найти xz′, yz′ в этой точке.

Имеем:

x2 (z) + y2 (z) ≡ z

2x xz′ +2 y yz′ ≡1

2 2 xz′ +2 (−2) yz′ =1

xz′ =0

−

≡

−2x′

−4 y′

≡1

−2x′

−4 y′ =1

=− 1

2x(z)

4 y(z)

y′

Уравнения касательной прямой и нормальной плоскости:

x −2	=	y +2	=	z −8	,	0	(x −2)− 1	(y +2)+1(z −8)=0
		− 1
0			1				4
	4

№ 31.3.

x2 + y 2 +z2 =50

x2 + y 2 −z2 =0

Выражая “мысленно” какие либо две переменные (например, ( y, z) ) через третью x , выступающую

в роли свободного параметра t , приходим к параметрическим уравнениям кривой:

x = x

y = y(x)z = z(x)

Найдем направляющий вектор касательной прямой в заданной точке (x0 , y0 , z0 ) =(3, 4,5) .

xx′		1
y′	= y′
x		x

zx′	zx′

Для этого необходимо найти yx′, zx′ в этой точке.

Имеем:
x2	+ y 2	(x) + z2	(x) ≡50	2x +2 y yx′ +2z zx′ ≡0
	+ y 2	(x) − z2	(x) ≡0		2x +2 y yx′ −2z zx′ ≡0
x2	+ y 2	(x) − z2	(x) ≡0		2x +2 y yx′ −2z zx′ ≡0

	4 y′	+5 z′	=−3	y′		=−	3
	4 y′	+5 z′	=−3	y′		=−
	x	x			x	4
4 y′		−5 z′	=−3			=0
	x	x		z′		=0
					x

Уравнения касательной прямой и нормальной плоскости:

x −3	=	y −4		=	z −5	,	1(x −3)−	3	(y −4)+0 (z −5)=0
			3
1		−		0			4
	4

Замечание. Не любая переменная может выступать в роли свободного параметра, т.е. не любые две переменные можно “мысленно” выразить через третью в окрестности заданной точки (в данном примере переменные (x, y) нельзя выразить через z , что очевидно из

геометрических соображений: кривая лежит в горизонтальной плоскости z = 5 ).

№ 31.4.

Координатные линии

	x =u cos v
L = y =u sin v			0	,	0	≤u ≤a
u		0			0
					0	≤v0 ≤2π

	z =v0

представляют собой горизонтальные отрезки лучей

x =r cosϕ0	, (0≤r ≤a, ϕ	0	=v	)	длины	a ,
		0	0
y =r sinϕ0			z =v0		под углом ϕ0 =v0
проведенных на высоте			z =v0		под углом ϕ0 =v0	к
оси Ox .	При изменении			параметра v0 :0→2π

координатная линия Lu , непрерывно перемещаясь, описывает винтовую поверхность (геликоид).

x =u0

Координатные линии Lv = y =u0

z =v

cos v	0		≤v ≤2π
sin v ,		0	≤u	≤1
			0

представляют собой витки винтовых линий радиуса r0 =u0 . При изменении параметра

u0 : 0 → a “расширяющееся” семейство координатных линий Lv																												описывает, разумеется,
ту же винтовую поверхность (геликоид).
Найдем направляющие векторы к координатным линиям:
								3			a											3												−	1	a
								3			a											3												−		a
u cos v								4						cos v								2				−u sin v								4
r = u sin v							=		1	a		,	r′ = sin v								=		1	,	r′=		u cos v						=		3		a
r = u sin v							=	4		a		,	r′ = sin v								=	2		,	r′=		u cos v						=				a
								4					u									2			v									4
	v	(	1		1	π )									0	(	1		1	π )							1		(	1		1	π )
	v		1	a,	1				1 π						0		1	a,	1				0				1			1	a,	1			1
				a,					1 π									a,					0								a,				1
		2 6						6								2 6													2 6
								6

Уравнения касательных прямых к координатным линиям:

			3													3					1
		x =								a +										(u −	2 a)
		x =		4						a +						2				(u −	2 a)
			1							1										1
Lu :	r =r (u0 ,v0 )+ ru′(u0 ,v0 )(u −u0 )	y =							a +									(u − 2 a)
Lu :	r =r (u0 ,v0 )+ ru′(u0 ,v0 )(u −u0 )	y =				4			a +				2					(u − 2 a)
				16 π +0 (u − 12 a)
		z =		16 π +0 (u − 12 a)
			3							1											1
		x =								a −							a			(v − 6 π )
		x =		4						a −				4			a			(v − 6 π )
	r =r (u0 ,v0 )+ rv′(u0 ,v0 )(v −v0 )					1						3						a (v − 16 π )
Lv :		y =				1		a +				3
Lv :		y =				4		a +				4
				1 π +1 (v − 1																	π )
		z =		1 π +1 (v − 1																	π )
			6																	6
Уравнения касательной плоскости:																								a (v −			π )
			3													3					1		1			1
		x =								a +									(u −		2 a)−					6
		x =	4							a +						2			(u −		2 a)−		4			6
r =r (u0 ,v0 )+ ru′(u0 ,v0 )(u −u0 ) +rv′(u0 ,v0 )(v −v0 )					1						1				(u − 12 a)+							3			a (v − 16 π )
		y =			1		a +				1											3
		y =			4		a +				2											4
			1 π +0 (u																	− 1 a)+1			(v − 1 π )
		z =	1 π +0 (u																	− 1 a)+1			(v − 1 π )
			6																	2			6

Найдем нормальный вектор к поверхности (к касательной плоскости):


													1
					i			j		k		2
					i			j		k		2
n =[ru′,rv′]=			3				1							3
										0	= −
				2				2		0	= −		2
			−		1	a	3		a	1		1
			−			a			a	1				a
			4				4							a
												2
Уравнения нормальной прямой:
											x	=					3		a +		1		t
											x	=			4				a +				t
															4					2
r =r (u		,v )+ n t														1				3
	0										y =					1		a −		3			t ,	−∞<t <+∞
											y =							a −					t ,	−∞<t <+∞
		0													4					2
															4					2
											z	=			1 π +					1		a t
											z	=			1 π +					2		a t
															6					2

№ 31.5.

Явное задание поверхности можно рассматривать как частный случай параметрического, когда в роли параметров выступают независимые переменные. Имеем:

	x		x
	y
r =	y	= y
				−2)
z(x, y)		xy (−1,		−2)

−1

=−2 ,2

i j k

−z′x

−y

n = r′,r′ =

0 z′

−z′

−x

1 z′y

(−1,

−2)

Уравнения касательной плоскости и нормальной прямой:

2 (x +1)+1(y +2)+1(z −2)=0,	x +1	=	y +2	=	z −2
	2
		1		1

№ 31.6.

Неявно заданную поверхность можно рассматривать, как поверхность уровня u = const =1

соответствующей функции u =u(x, y, z) =	x2	+	y 2	−	z2	. В таком случае роль нормального
	a2		b2		c2

вектора к поверхности может играть вектор градиента этой функции:

x r = y

z (x0

	x0
	= y	,
, y0	0
, y0	, z0 )
	z0


			2x
ux′			a2
ux′			2 y
n =grad u = u′	=		2 y
n =grad u = u′	=		b2
y			b2
u′				2z
z		−		2z
		−		c2
				c2

Уравнение касательной плоскости:

(x0

	2x0

		a	2

=	2 y0

		b	2

		2z0
−

		c		2
, y0 , z0 )

(x −x

2 y

(y − y

)−

(z −z

)=0

−

0 =

−

xx0 + yy0 − zz0 =1.

a2 b2 c2

32. Двойные интегралы. Физические и геометрические приложения

Условия.

№ 32.1. Найти массу пластины, ограниченной заданными кривыми, с поверхностной плотностью ρ = ρ(x, y) .

y = x, y = 0, x =1; ρ =xy3 .

y = x, y =1, x = 0; ρ =x3 y.

№ 32.2. Найти заряд пластины, ограниченной заданными кривыми, с поверхностной плотностью ρ = ρ(x, y) .

y =1, y = x2 , x ≥0;	ρ =cos	x	.	y =1, y = x, x =0; ρ =sin	x	.

		y			y2

№ 32.3. Найти центр масс пластины, ограниченной заданными кривыми, с поверхностной плотностью ρ = ρ(x, y) .

y = x, y = x2 ; ρ = xy.	y = x, y = x3 ; ρ = x2 y.

Найти объем тела, ограниченного поверхностями.

№ 32.4.	z=2−x−2 y, z=0, x=0, y=0, x+y=1.	№ 32.4.	z=2x+y, z=0, x=0, y=0, 2x+y=2.
№ 32.5.	z = xy, z = 0, x + y =1.	№ 32.5.	z = xy, z = 0, y = x, x =1.

Найти площадь пластины, ограниченной кривыми.

№ 32.6. y =ex ,

y =0, x =0, x =1.

№ 32.6.

y =

y =0,

x =0,

x =1.

1+ x2

№ 32.7. y =

y = 2 x,

y =1.

№ 32.7.

y = ln

y = 0,

y =1,

x = 0.

Изменить порядок интегрирования.

№ 32.8. ∫2 (

∫x

f (x, y)dy

)dx.

№ 32.8. ∫1 (

e∫x

f (x, y)dy

)dx.

2 x

№ 32.9. ∫2 (

2 x∫-x2

f (x, y)dy

)dx.

№ 32.9. ∫π (

sin∫x

f (x, y)dy

)dx.

Теория.

Пусть в области D задана функция

f (x, y) .

Разобьем область D кривыми на малые попарно не налегающие части Dk

D =D1 ... Dk ... Dn ,

с площадью ∆k S и обозначим через d =max dk диаметр разбиения.

1≤k≤n

Выберем на каждой части промежуточную точку (ξk ,ηk ) Dk .

Составим интегральную сумму

∑ f (ξk ,ηk )∆k S.

k =1

Двойным интегралом называется предел интегральных сумм, когда диаметр разбиения стремится к нулю

	n
dlim→0	∑ f (ξk ,ηk )∆k S = ∫∫f (x, y)dxdy,
	k =1	D
		D

если он существует, конечен и не зависит ни от способа разбиения, ни от выбора промежуточных точек.

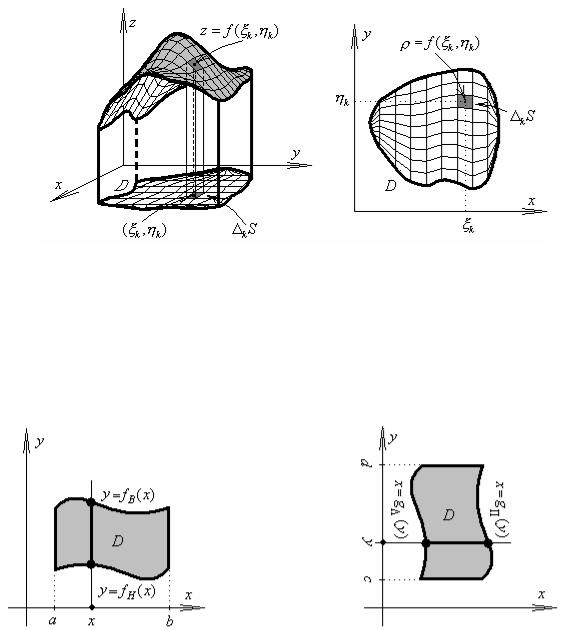
n	n	n	n
V =∑	∆kV ≈∑ f (ξk ,ηk )∆k S	m =∑∆k m ≈∑ f (ξk ,ηk )∆k S
k =1	k =1	k =1	k =1
Геометрический смысл: объем под поверхностью z = f (x, y),			(x, y) D .

Физический смысл: масса (заряд) пластины D с поверхностной плотностью ρ = f (x, y) .

Если область D имеет вид “криволинейной трапеции”,

D ={a ≤ x ≤b, fH (x) ≤ y ≤ fB (x)}

D ={c ≤ y ≤d, gΛ ( y) ≤ x ≤ gΠ ( y)}

то двойной интеграл может быть сведен к повторному:

∫∫f (x, y)dxdy =∫b (		fB∫( x)	f (x, y) dy )dx
D	a	fH ( x)

∫∫f (x, y)dxdy =∫d (		gΠ∫( y)	f (x, y) dx )dy
D	c	gΛ ( y)

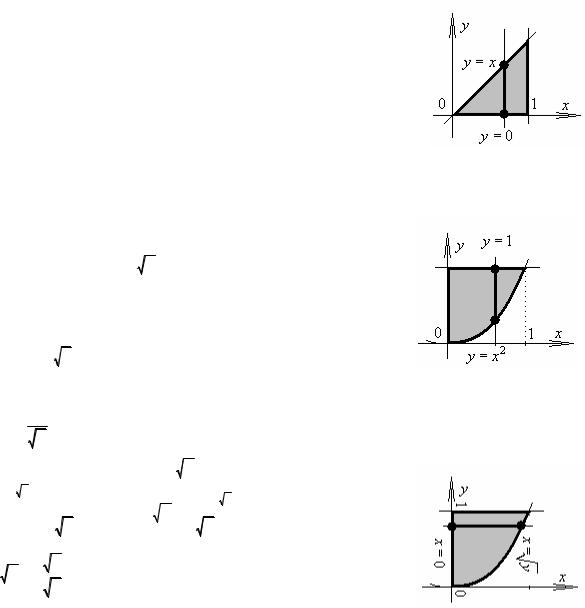
Решения.

№ 32.1.

m =∫∫ρ(x, y)dxdy =∫∫x y3dxdy =→

D	D
	D ={0 ≤ x ≤1, 0 ≤ y ≤ x}

→=∫1 ( ∫x x y3dy )dx =∫1 ( x∫x												y3dy )dx =
0	0						0			0
1				x			1
=∫x	1		4		1		∫x	5				1	1	6	1	1
	1		4		1			5				1	1	6	1	1
	4 y				dx = 4				dx =			4	6 x		0 =		.
				0					dx =							24	.
				0												24
0							0
№ 32.2.
q =∫∫ρ(x, y)dxdy =∫∫cos										x	dxdy =→
q =∫∫ρ(x, y)dxdy =∫∫cos										y	dxdy =→
D							D
	D ={0 ≤ x ≤1, x2 ≤ y ≤1}
→=∫1 (	∫1	cos			x	dy	)dx =∫1 (?						1x2 )dx =?
					x
					y
					y
0	x2									0

Трудностиснахождениемпервообразнойможнообойти, изменивпорядокинтегрирования: q =∫∫cos xy dxdy =→

D ={0 ≤ y ≤1, 0≤x ≤ y}

→=∫1 (	∫y cos		x		dx )dy =∫1		y sin	x	y dy =
			x					x
				y				y
0	0					0			0
0	0					0			0
1		y	1			1				3	1
1			1			1				3	1
=∫				dy =sin1∫y		2			2	2			2
=∫	y sin	y		dy =sin1∫y			dy =sin1		3 y		0	=	3 sin1.
0			0

№ 32.3.

При нахождении центра масс неоднородной пластины D , с поверхностной плотностью ρ =ρ(r ) =ρ(x, y) и массой

m =∫∫ρ(r )dS =∫∫ρ(x, y)dxdy ,

D D

воспользуемся определением центра масс системы материальных точек. Разобьем область D кривыми на малые, попарно не налегающие части Dk с массами

∆k m ≈ ρ(ξk )∆k S = ρ(ξk ,ηk )∆k S , настолько малые, что каждую можно рассматривать как материальную точку ξk =(ξk ,ηk ) . Тогда

= m ∫∫xρ(x, y)dxdy

1 n

∫∫r ρ(r )dS

r0 ≈

∑ξk ∆k m ≈

∑ξk ρ(ξk )∆k S d→→0

∫∫yρ(x, y)dxdy

k =1

Найдем массу пластины:

m =∫∫ρ(x, y)dxdy =∫∫xydxdy =→

D	D
	D ={0 ≤ x ≤1, x2 ≤ y ≤ x}

→=∫1	(	∫x	xydy	)dx =∫1	(	x∫x	ydy	)dx = 12 ∫1					x y2	xx	2 dx =
			xydy				ydy						x y2		2 dx =

0		x2		0		x2			0
	1
= 12 ∫(x3 − x5 ) dx = 12 (14 x4 − 16 x6 )										1	1
										1
										0 =		.
										0 =	24	.
	0

Найдем координаты центра масс:

x0 = m1 ∫∫xρ(x, y)dxdy = m1 ∫∫x xydxdy = m1 ∫

D D 0

= 21m ∫(x2 y2 xx2 )dx =

(	∫x	x2 ydy			)dx =		1		∫1	(		x2 ∫x			ydy			)dx =
(	∫x	x2 ydy			)dx =		m		∫1	(		x2 ∫x			ydy			)dx =
	x2							0					x2
1	1							1				1				1		)	1	1		24
			4		6								5				7		1
			4		6								5				7
2m ∫(x				− x		) dx =					(5 x			−		7 x			0 =		=	35 .
2m ∫(x				− x		) dx =		2m			(5 x			−		7 x			0 =	35m	=	35 .
	0

y0 =

∫∫yρ(x, y)dxdy =

∫∫y xydxdy =

∫1 (

∫x

xy2 dy

)dx =

∫1 (

x∫x

y2 dy

)dx =

)

1 1

∫(xy

)dx =

∫(x

− x

)

dx =

(5 x

−8 x

0 =

= 40 .

40m

№ 32.4.

V =∫∫( fB (x, y) − fH (x, y))dxdy =→

Выделим среди поверхностей {z =2 − x −2 y, z =0,

x =0,

y =0,

x + y =1}, ограничивающих

объем V ,

те, уравнения которых не содержат переменной

z .

На плоскости

xOy эти

уравнения задают некоторые кривые, а в пространстве – цилиндрические поверхности, параллельные оси Oz , в основании которых лежат эти кривые. В данном примере прямые {x = 0, y = 0, x + y =1} ограничивают некоторую область D , так что плоскости

{z = 0 ≤ z = 2 − x − 2 y, (x, y) D}, играющие роль “нижней” и “верхней”, достаточно построить схематично.

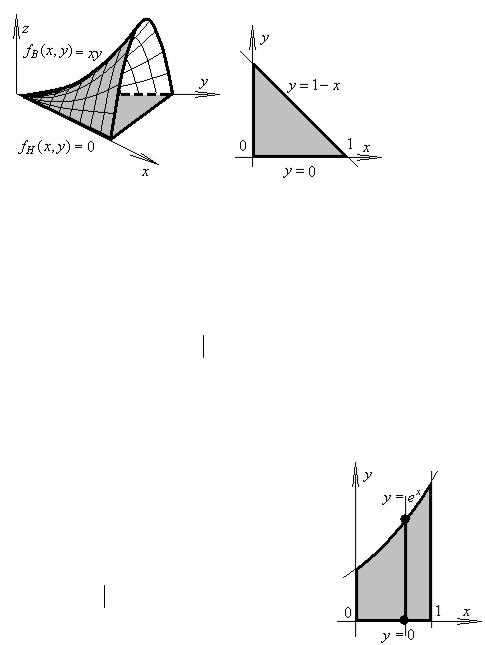
→=∫∫((2 − x −2 y)−0)dxdy =[D ={0 ≤ x ≤1,				0≤ y ≤1− x}]=∫1 (		1∫−x (2 − x −2 y)dy )dx =
D					0	0
1	1				1
=∫((2 − x) y − y2 )		10−x dx =∫((2 − x)(1− x) −(1− x)2 )dx =∫(1− x)dx =(x − 12 x2 )					1
							1
							0 = 12 .
							0 = 12 .
0	0				0
№ 32.5.
V =∫∫( fB (x, y) − fH (x, y))dxdy =→
D
Выделим среди поверхностей { z = xy,				z =0, x + y =1}, ограничивающих объем V ,				те,
уравнения которых не содержат переменной z . В данном примере прямая {y =1 − x}								не
ограничивает	никакую область		D , так что поверхности			{ z = xy, z = 0} необходимо
построить достаточно точно:			z = xy – седловая		поверхность, z = 0 – горизонтальная
плоскость, пересекающиеся по осям координат Ox,					Oy.

= 12 ∫	(x −2x2 + x3 )dx = 12 (12 x2 − 32 x3 + 14 x4 )				1	1
					1
					0 =		.
					0 =	24	.
0						D ,		“нижней” и “верхней” поверхностей
Из рисунка видно, что играет роль области						D ,		“нижней” и “верхней” поверхностей
{z = 0 ≤ z = xy, (x, y) D}.
→=∫∫(xy −0)dxdy =→
D				D ={0 ≤ x ≤1, 0 ≤ y ≤1 − x}
1	1−x	1	1−x	1		1−x		1
→=∫(	∫ xydy	)dx =∫(	x ∫	ydy )dx = 12 ∫xy2		0		dx = 12 ∫x(1− x)2 dx =
0	0	0	0	0				0
1
№ 32.6.

S =∫∫1 dxdy =→

D ={0 ≤ x ≤1, 0 ≤ y ≤ex }

→∫1 ( e∫x 1 dy )dx =∫1 (ex −0)dx =ex 10 =e −1.

0 0 0

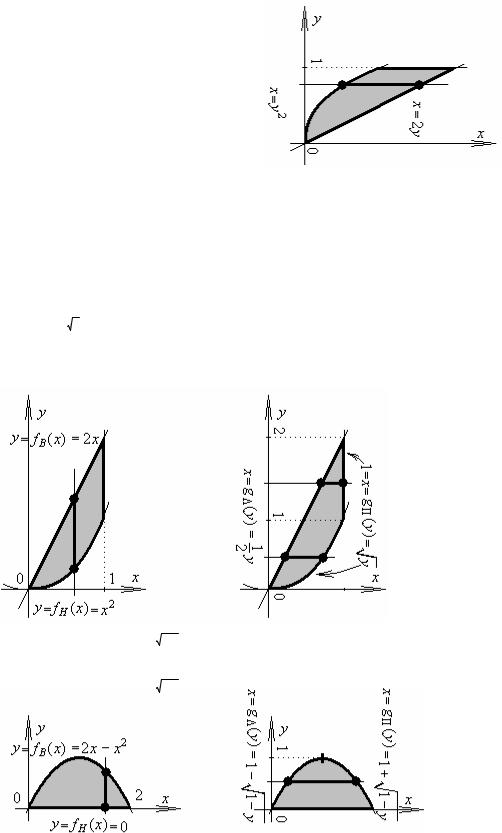
Сравнить: нахождение площади “криволинейной трапеции” с помощью двойного интеграла с нахождением площади с помощью однократного интеграла:

S =∫∫1 dxdy =[D ={a≤x≤b, fH (x)≤ y ≤ fB (x)}]=∫b (				fB∫( x)	1 dy	)dx =∫b ( fB (x)− fH (x))dx
D			a	fH ( x)		a
№ 32.7.
S =∫∫1 dxdy =→
D
	D ={0 ≤ y ≤1, y2 ≤ x ≤ 2 y}
1	2 y	1
→=∫( ∫1 dx )		dy =∫(2 y − y2 )dy =(y2 −13 y3 )	1
			1
			0 = 32 .
0	y2	0

S =∫∫1 dxdy =[D ={c ≤ y ≤d, gΛ ( y) ≤ x ≤ gΠ ( y)}]=∫d (					gΠ∫( y)	1 dx	)dy =∫d (gΠ ( y) − gΛ ( y))dy
D				c	gΛ ( y)		c
№ 32.8.
∫1 ( 2∫x f (x, y)dy )dx =∫1 ( ∫y			f (x, y)dx )dy +∫2 ( ∫1		f (x, y)dx )dy.
0 x2	0	1 y	1	1 y
		2		2

№ 32.9. ∫2	(	2 x∫-x2	f (x, y)dy	)dx =∫1	(	1+	∫1−y	f (x, y)dx )dy.
0		0		0		1−	1−y

<<< < Предыдущая 1 2 34 / 144 5 6 7 8 9 10 11 12 13 14 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
23.02.201534.74 Кб11маркетинг (робота с Ирой).docx
#
12.11.2019365.57 Кб9маркетинг услугТ 1-4.doc
#
23.02.201539.71 Кб5Маркетинг.docx
#
01.05.2019275.97 Кб3Маркетингова географія Л.1.doc
#
23.02.2015173.28 Кб16мат.методы.docx
#
23.02.20151.44 Mб69матан.pdf
#
23.02.20152.78 Mб86Матем. анализ. Методичка(1 семестр).doc
#
13.03.20161.44 Mб37Матеріали до словника 2.doc
#
13.03.2016105.98 Кб4материаловедение Лекция 1.doc
#
25.08.201938.33 Кб4Материалы 3_1.docx
#
10.11.2019241.66 Кб1материалы для лекции 1.doc