матан

Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Харьковский Национальный Университет им. В. Н. Каразина

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

<+1 −3<x<+3,

.pdf

Скачиваний:

Добавлен:

23.02.2015

Размер:

1.44 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 1011 / 1411 12 13 14 > Следующая >>>

Степенной ряд можно почленно дифференцировать и интегрировать внутри интервала сходимости

∞

∑an xn =∑an

xn =∑an nxn−1

∫

∑antn dt =∑an

∫tn dt =∑an

n +

n=0

n=1

n=0

Коэффициенты an можно выразить через сумму степенного рядаS(x):

Рядом Тейлора функции f (x) называется степенной ряд

f (x) =∑∞ f (n) (0) xn .

n=0 n!

a =	S(n) (0)	.

n	n!

Отметим наиболее употребительные разложения функций в ряд Тейлора:

∞

ex =

∑

=1+

+...+

+...

(−∞< x <+∞) ,

n=0

∞

x2n+1

sin x =

∑(−1)n

−

+...+(−1)n

+...

(−∞< x <+∞) ,

(2n +1)!

n=0

∞

x2n

cos x =

∑(−1)n

=1−

−...+(−1)n

+...

(−∞< x <+∞) ,

(2n)!

n=0

(2n)!

∞

ln(1+ x) =∑(−1)n+1

= x

−

+...+(−1)n+1

+...

(−1< x ≤+1) ,

n=1

∞

=1+αx +α(α −1)

x2 +...+α(α −1)...(α −n +1) xn +...

(1+ x)α =∑Cαn xn

(−1< x <+1) .

n=0

В частности, при α = −1,

x → −x

получаем известную формулу суммы геометрической

прогрессии:

∞

=∑xn = 1+ x + x2 +...+ xn +...

(−1< x <+1) .

1− x

n=0

Решения.

№ 44.1.

∞

∑

an+1

n=0 n

(n +1) +1

an+1 =

lim

an+1

= lim

n2 +1

=1=q

R =1 =1

(

n→∞

n→∞ n2 +2n+2

Ряд сходится внутри интервала (−1, +1) ,

расходится

вне

этого

интервала. Проверим

поведение ряда на концах:

∞

(−1)n

x =−R =−1

∑

=∑

сходится;

n=0

x=−1

n=0

∞

x =+R =+1

∑

=∑

p =2

сходится.

n=0

x=+1

n=0

n +1

Замечание. Сходимость первого ряда, очевидно, следует из сходимости второго (ряда из “модулей”).

Итак, областью сходимости исходного степенного ряда является замкнутый интервал

[−1, +1] .

№ 44.2.

∞	xn			1					1
∑			an =		,	an+1	=
	n			n				n+1	(n +1)
n=1	2	n		2 n			2

an+1	=	1	2n n
a	=	2n+1(n +1)	1
n

Ряд сходится внутри интервала поведение ряда на концах:

lim	an+1	= lim	n		= 1	=q	R = 1	=2.
	a
n→∞		n→∞ 2(n +1)			2		q
	n
(−2, +2) , расходится			вне	этого		интервала. Проверим

∞

(−2)n

∞

(−1)n

x =−R =−2

∑

=∑

= ∑

0 сходится;

n=1 2

x=−2 n=1

n=1

∞

x =+R =+2

∑

=∑

∑

p =1

расходится.

n=1 2 n

x=+2 n=1

2 n

n=1

Итак, областью сходимости исходного степенного ряда является полуоткрытый интервал

[−2, +2) .

№ 44.3.

∞	2n		1	,	m =2n	lim	am+1 = ,	lim m am = .
∑x n		am =	3n			lim	am+1 = ,	lim m am = .
	3					m	am	m
n=0	3	0,			m =2n+1	→∞		→∞
n=0		0,			m =2n+1

Воспользовавшись закономерностью в появлении только четных степеней x2n =(x2 )n ,

сделаем замену переменной y = x2

и рассмотрим вспомогательный ряд:

∞ yn

R = 1

∑

bn =

lim n

= lim n

=3.

n=0 3

n→∞

3 3

Вспомогательный ряд сходится внутри интервала (−3, +3) , расходится вне этого интервала. Проверим поведение ряда на концах:

	∞		∞	(−3)n		∞
y =−R =−3	∑ ynn		=∑	(−3)n	n	= ∑(−1)n	(−1)n → 0	расходится;
	n=0	3	y=−3 n=0	3		n=0
	∞		∞	(+3)n		∞
y =+R =+3	∑ ynn		=∑	(+3)n	n	= ∑ 1	1 → 0	расходится;
	n=0	3	y=+3 n=0	3		n=0

Итак, областью сходимости вспомогательного ряда является открытый интервал (−3, +3) . Следовательно,

−3< y <+3 −3<x2 <+3 x2 <+3 − 3 < x <+ 3 ,

так что областью сходимости исходного ряда является открытый интервал (− 3, + 3) .

№ 44.4.

∞

n∑=0 (2nx+n1)!!

an = (2n1+1)!!,

an+1	=	1
a		(2n +3)
n

an+1 =

=an

(2(n +1)+1)!!

(2n +3)!!

(2n +3)

an+1

=0 =q R =

= 1

lim

= lim

=∞.

n→∞

n→∞ (2n +3)

Итак, областью сходимости исходного степенного ряда является вся ось (−∞, +∞) .

№ 44.5.

∞

= lim ln n =∞=q R = 1

= 1

∑

lnn n xn

=lnn n n

=n lnn n =ln n lim n

=0.

n→∞

∞

n=0

Итак, областьюсходимостиисходногостепенногорядаявляетсяединственнаяточка x0 = 0 .

№ 44.6.

∞

S(x) =n∑=0 nx+n1

Нетрудно видеть, что область сходимости данного ряда полуоткрытый интервал [−1, +1) . Имеем:

∞

S(x) x =∑

x =∑

xn+1

n+1

n=0

∞

xn+1

∞

xn+1

∞

(S(x) x)=

∑

=∑(n +1)

=∑xn =

n+1

1−x

n=0

x		x
	d	1			x

S(x) x =∫		(S(t) t )dt =∫		dt =−ln(1−t)	0
	dt		1−t

0		0

=−ln(1−x)

∞

=− ln(1−x) , x [−1,

S(x) =∑

+1).

n=0

n+1

Замечание. Полагая, например,

x = −1, x =− 1 ,

x =+1

и т.д., получим суммы некоторых

числовых рядов:

∞

(−1)n =− ln(1−(−1))

∞

(−1)n

=ln 2,

S(−1) =∑

∑

n=0

n+1

(−1)

n=0

n+1

(− 1 )n

(1−(− 12 ))

(

∞

(

−1

=∑

=−

∑

−1

=2ln

3 ,

(− 12 )

2 )

n=0

n+1

n=0 (n

+1)2n

∞

1 n

ln 1−

∞

(n3+)1 =−

3 )

S (

1 )=∑

(

∑

=−3ln 2 =3ln 3 .

(3 )

(

)

n=0

n=0 n +1 3

№ 44.7.

∞

S(x) =∑nxn

n=1

Нетрудно видеть, что область сходимости данного ряда открытый интервал (−1, +1) . Имеем:

S(x)

∞

=∑nxn 1

=∑nxn−1

n=1

S(t)

∞

n−1

∞

n−1

∞

n+1

∞

∫

=∫

∑nt

=∑

∫ nt

dt =∑n n

=∑x

= x∑x

1−x

0 n=1

n=1 0

n=1

n=0

S(x)

∫x S(t) dt

= (1−x) − x2(−1)

dx 1−x

(1−x)

∞

S(x) =∑nxn =

x (−1, +1)

(

n=1

1−x

Замечание.

Полагая,

например,

x =− 1

x =+1

и т.д., получим суммы некоторых

числовых рядов:

(

∞

−1

∞

S (−1 )=∑n(−

1 )n =

2 )

∑(−1n)

n =− 2

(1−(−12 ))

n=1

∞

S (1 )=∑n(1 )n

∑

3 .

(1−13 )

n=1

n=1 3

№ 44.9.

f (x) =

−

2 +

−

(x−2)(x+3)

(x −2)

(x+3)

Учитывая, что:

∞

=−

=−1 ∑

=−∑

(x −2)

(1−

)

2 n=0

(2 )

n=0

2n 1

∞

=1 ∑

−

=∑(−1)n

(x+3)

3(1−(−

))

3 n=0 (

3 )

n=0

получим:

∞

3n+1 +(−1)n 2n+1

f (x) =

=−∑

−∑(−1)

=−∑

n+1

xn , −2< x <+2.

+x−6

n+1

n=0

№ 44.10.

(

)n )

−x

∞

(

−

∞

(

f (x) =ch x = e

= 1

∑

+∑

1 ∑

−1

n=0

2 n=0

Замечая, что

(

)n )

0 , n =2m +1

a =

−1

, n =2m

2 n!

(2m)!

получим:

∞

x2m

ch x = ∑

x (−∞, +∞)

m=0

(2m)!

№ 44.11.

f (x) =arctg x	d	f (x) =	d	arctg x =	1	.
	dx		dx		1+ x2
Учитывая, что

∞

(

2 )n

∞ (

(

2 )

∑

−x

−1<

−x

<+1

−1< x <+1,

1+ x2

=∑

−1

1−(−x2 )

n=0

получим:

∞

x2n+1

arctg x =∫

arctg tdt =∫

dt =∫∑(−1)n t2n dt =∑

(−1)n ∫t2n dt =∑(−1)n

−1< x <+1.

1+ x

(2n +1)

0 n=0

n=0

Очевидно, на обоих концах x = ±1 ряд сходится. Итак,

∞

x2n+1

arctg x =∑(−1)n

−1≤ x ≤+1.

(2n +1)

n=0

Замечание. Полагая,

например,

x =1,

получим сумму некоторого числового ряда,

позволяющего, в частности, приближенно найти число π :

∞

(

arctg 1=∑(−1)

π =4∑

−1

(

)

(

)

n=0

2n +1

n=0

2n +1

№ 44.12.

−x

1 ∞

(

−x

2 )n

1 ∞ (

∞ (

)n 1

∞ (

2n+1

∞

(

∫e

dx =∫∑

=∫∑

−1

dx =

∑

−1

∫x

=∑

−1

=∑

−1

2n +1

n!(2n +1)

0 n=0

n=0

0 n=0

=1−

−

+...=

1!(2 1+1)

2!(2 2 +1)

3!(2 3+1)

4!(2 4 +1)

5!(2 5 +1)

=1−

1 +

−

+...=1−

−

−...≈0.747

1320

216

Замечание. При определении числа слагаемых, которое достаточно взять для достижения

заданной точности,	воспользуемся тем, что для знакочередующегося ряда имеет место
оценка	∞
	∞
	S =∑(−1)n an	(an 0)	S −Sn	≤an+1 .
	S =∑(−1)n an	(an 0)	S −Sn	≤an+1 .
	n=0
В данном случае,	заданная точность	ε = 0,001 достигается, если взять первые пять
слагаемых.

45. Ряды Фурье

Условия.

Разложить функцию в ряд Фурье на интервале [−π, +π ] . Построить график суммы ряда

Фурье. Полагая x = 0 , x =π					, x =π , найти суммы получающихся числовых рядов.
				2
№ 45.1.	f (x) = x					№ 45.1.	f (x) =1
№ 45.2.	f (x) =	x				№ 45.2.	f (x) = sign x
№ 45.2.	f (x) =	x				№ 45.2.	f (x) = sign x
№ 45.3.	f (x) =		0,	−π	≤ x < 0	№ 45.3.	x +π, −π ≤ x < 0
№ 45.3.	f (x) =		0,	−π	≤ x < 0	№ 45.3.	f (x) = 0,	0 ≤ x ≤ +π
		π − x,		0	≤ x ≤ +π
№ 45.4.						№ 45.4.	f (x) = cosαx
№ 45.4.	f (x) = sinαx					№ 45.4.	f (x) = cosαx

Теория.

Если функция y = f (x) кусочно-непрерывно дифференцируемая в интервале длиной 2π (например, [−π, +π ] , [0,2π], [a, a + 2π ] ), причем точки разрыва x0 регулярны

f (x0 ) =	f (x0	+0) + f (x0	−0)	,
f (x0 ) =		2		,
		2

то ее можно представить рядом Фурье:

f (x) = a0

∞

+∑(an cos nx +bn sin nx),

−π ≤ x ≤+π

n=1

an =

+∫π

f (x) cos nxdx,

n =0, 1, 2,...

bn =

+∫π

f (x)sin nxdx,

n =

1, 2,...

−π

Если дополнительно функция

y = f (x)

(−π ≤ x ≤ +π)

четная или нечетная,

то ее ряд

Фурье имеет соответственно только четную или нечетную составляющую:

четная

∞

нечетная

f (x) = a0

+∑an cos nx,

−π ≤ x ≤+π

f (x) =∑bn sin nx,

−π ≤ x

≤+π

n=1

an =

+∫π

f (x) cos nxdx,

bn =0.

an =0,

bn =

+∫π

f (x)sin nxdx.

Отсюда вытекает возможность разлагать функцию, заданную только на интервале [0,π] , в ряд по Cos или по Sin, представляющие собой ряды Фурье соответственно

четного или нечетного продолжений функции на интервал [−π,0] :

		a0		∞		∞
f (x) =				+∑an cos nx	=∑bn sin nx,				0 < x <+π

2				n=1		n=1

an =	2		+∫π	f (x) cos nxdx,		bn =	2	+∫π	f (x)sin nxdx.
	π						π
0						0

При нахождении коэффициентов ряда Фурье полезно помнить:

- интегралы от функций cos(...) , sin(...) по интервалу длины период (или несколько периодов) равны нулю:

+∫π cos nxdx =+∫π sin nxdx =0;

−π		−π
cos nπ =(−1)n , sin nπ =0, cos n π	= (−1)m ,		n =2m	,	sin n π	= 0,	n =2m .
2		0,	n =2m +1		2	(−1)m , n =2m +1

Решения.

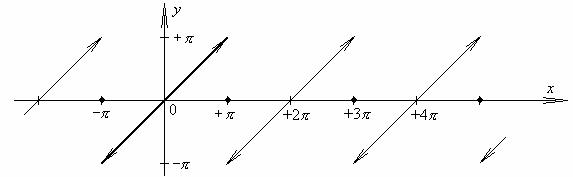
№ 45.1.

График суммы ряда Фурье является 2π – периодическим продолжением на всю ось графика данной функции y = f (x) (−π ≤ x ≤ +π) , с регулярными точками разрыва.


Найдем коэффициенты ряда Фурье:					an
Функция	f (x) = x – нечетная на интервале [−π, +π ]				an	= 0.
bn =π2 π∫ f (x) sin nxdx =π2 π∫x sin nxdx =−π2n π∫xd cos nx =−π2n (						x cos nx	π0 −π∫cos nxdx )=


0	0		0			0
=−π2n (π cos nπ − 1n sin nx		π0 )=−π2n (π (−1)n −0)=− n2 (−1)n = n2 (−1)n+1 .


Итак,
		∞ (	)n +1
		x =∑	−1	sin nx,	−π < x <+π .
		x =∑	n	sin nx,	−π < x <+π .
		n=1

Используя полученное разложение, с учетом вида графика суммы ряда Фурье, из которого

видно к чему сходится ряд в точках разрыва, найдем суммы некоторых числовых рядов: x = 0

∞

(

)n +1

sin n0

∞

(

)n +1

0 =0 ;

0 =2∑

−1n

=2∑

−1n

n=1

x =π

∞

(

)n +1

∞

(

)2m + 2

∞

(

=2∑

−1

sin n π

2∑

−1

sin (2m+1)π

=2∑

(−1)m

∑

−1

=π

;

2m+1

n=1

m=0

2m+1

m=0

2m+1

x =π

∞

(

)n +1

sin nπ

∞

(

)n +1

=0.

0 =2∑

−1n

=2∑

−1n

n=1

Сравнить с № 40.11.

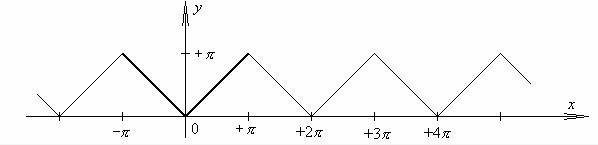
№ 45.2.

График суммы ряда Фурье является периодическим продолжением на всю ось графика данной функции y = f (x) (−π ≤ x ≤ +π) .

Найдем коэффициенты ряда Фурье:

Функция f (x) =

– четная на интервале [−π, +π ]

bn = 0.

2 x2

a0 =

∫ f (x)dx =

∫xdx =

=π,

an =π2 π∫ f (x) cos nxdx =π2 π∫x cos nxdx =π2n π∫xd sin nx =π2n (

x sin nx

π0 −π∫sin nxdx )=

=π2n (0 + 1n cos nx

π0 )=

n =2m

(cosπn −1)=

((−1)n −1)=

−4

, n =2m +1

πn2

π(2m +1)2

Итак,

∞

=π

−

∑

cos (2m +1)x,

−π ≤ x ≤+π .

(2m +1)

π m=0

Используя полученное разложение, с учетом вида (непрерывности) графика суммы ряда Фурье, найдем суммы некоторых числовых рядов.

x = 0
0 =π			4				∞		1						=π −	4				∞			1				∞		1			=π 2
	−		4			∑			1				cos (2m +1)0			4			∑				1				∑		1					;
	−					∑		(2m +			2		cos (2m +1)0						∑					2			∑	(2m +1)		2				;
2		π m=0						(2m +			1)				2	π m=0 (2m +1)											m=0	(2m +1)					8
x =π
2							∞														∞
π =π					4		∞			1				cos (2m +1)π =π					4		∞		1			=π
		−			4		∑			1						−			4		∑		1		0		;
		−					∑			(2m +1)		2				−					∑			2	0		;
2 2 π m=0										(2m +1)					2 2			π m=0					(2m +1)			2
x =π
π =π				4			∞		1					cos (2m +1)π =π +			4				∞		1				∞		1				=π 2 .
		−		4		∑			1								4			∑			1				∑		1
		−				∑					2									∑		(2m +		2			∑		(2m +1)		2
2 π m=0									(2m +1)						2	π m=0						(2m +		1)			m=0		(2m +1)				8

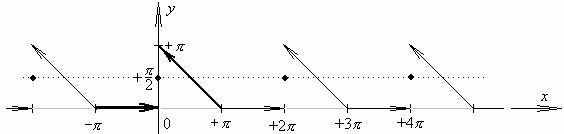
№ 45.3.

“Подправим” функцию, изменив ее в точке разрыва x0 =0 регулярным значением:

		f (0) = f (x	) =	f (x0 +0) + f (x0 −0)	=π +0 =π .
		f (0) = f (x	) =		=π +0 =π .
		0	2		2	2
		−π ≤ x <0	2		2	2
	0,	−π ≤ x <0
f (x) =	π ,	x =0
	2	0 < x ≤+π
π − x,		0 < x ≤+π

График	суммы ряда Фурье является 2π - периодическим					продолжением на всю ось
графика данной функции y = f (x)			(−π ≤ x ≤ +π) , с регулярными точками разрыва.

Найдем коэффициенты ряда Фурье. Функция f (x) ни четная, ни нечетная.

1 (π − x)2

a0 =

∫

f (x)dx =

∫(π − x)dx =−

2 ,

−π

a =

f (x)cos nxdx=1

(π−x)cos nxdx=

(π−x)d sin nx= 1

(

(π−x)sin nx

sin nxdx

n π

∫

πn ∫

πn

∫

−π

n=2m

=−

cos nx

=−

(cos nπ−1)=−

(

(−1)n −1)=

n=2m+1

πn2

π(2m+1)2

bn =

∫

f (x)sin nxdx =π

∫(π − x)sin nxdx =−πn

∫(π − x)d cos nx =

−π

π0 )= 1n

=−π1n ( (π − x) cos nx

π0 +π∫cos nxdx

)=−π1n (−π + 1n sin nx

Итак,

∞

f (x) =π

1 sin nx,

∑

cos (2m +1)x +∑

−π ≤ x ≤+π .

(2m +1)2

4 π m=0

n=1 n

Используя полученное разложение, с учетом вида графика суммы ряда Фурье, из которого видно к чему сходится ряд в точках разрыва, найдем суммы некоторых числовых рядов:

x = 0

π =π

∞

1n sin n0

=π

∞

=π 2

∑

cos (2m +1)0 +∑

∑

;

(2m +1)

2 4 π m=0

n=1

π m=0

(2m +1)

m=0

(2m +1)

x =π

∞

(−1)

∞

(−1)

π =π

∑

cos (2m +1)π

+∑1n sin n π =

+ ∑

∑

=π

;

(2m +1)

(2m+1)

2 4 π m=0

n=1

m=0

x =π

0 =π +

∞

1n sin nπ

=π

∞

=π 2 .

∑

cos (2m +1)π +∑

−

∑

π m=0 (2m +

n=1

π m=0

(2m +1)

m=0 (2m +1)

Замечание. Коэффициенты an , bn

можно найти “одновременно”:

∫

f (x)cos nxdx

an =π

−π

∫

f (x)e

−inx

dx=

=π

−ibn =π

f (x)(cos nx−isin nx)dx=π

∫

f (x)sin nxdx

−π

π0 )=

)=−π1in (−π−

=π1

∫(π−x)e−inxdx=−π1in ∫(π−x)de−inx =−π1in (

(π−x)e−inx

π0 +∫e−inxdx

e−inx

=−π1in (−π−

(e−inπ −1))=−π1in

(−π−

(cos nπ−1))=−π1in (−π−

((−1)n −1))=

((

)

((

)

=in−πn2

−1

−1 =−

πn2

−1

−1 −i n

((

)

((

)

n =2m

an −ibn =−

πn

−1

−i πn

=−π

−1

n =2m +1,

bn = n

(

2m +1

c =

an −ibn

1 ((

)

−i

По существу найдены коэффициенты

=−

−1

ряда Фурье в

комплексной форме:

∞

)einx

f (x) = ∑ cneinx = ∑ (−

((−1)n −1)−i

(−π ≤ x ≤+π).

π 2

n=−∞

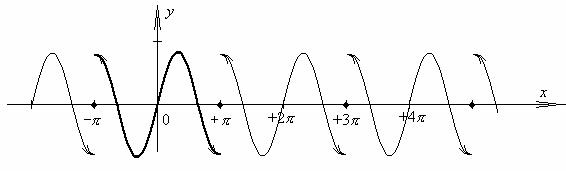
№ 45.4.

является 2π - периодическим продолжением на всю ось

График

суммы

ряда Фурье

графика данной функции , y = f (x)

(−π ≤ x ≤ +π)

с регулярными точками разрыва.

Очевидно, если α = n – целое число, то “рядом”

Фурье функции

f (x) = sin nx

является

сама функция (т.е. все остальные слагаемые ряда равны нулю). Пусть α =/ n – нецелое.

Найдем коэффициенты ряда Фурье.

an =0.

Функция f (x) = sinαx – нечетная на интервале [−π, +π ]

−sin(αα++nn)x )

bn =π2 π∫sinαxsin nxdx=π2 12 π∫(cos(α −n)x−cos(α+n)x)dx=π1 (sin(αα−−nn)x

sin(α −n)π

sin(α +n)π

sinαπ cos nπ −cosαπ sin nπ

sinαπ cos nπ +cosαπ sin nπ

(

α −n

−

α +n

)=π

(

−

α −n

α +n

sinαπ(−1)n

−

sinαπ(−1)

−

sinαπ(−1)

α −n

α +n

(α −n

α +n )

α2 −n2

Итак,

∞

sinαx =π2 sinαπ ∑(−1)n

sin nx,

−π < x <+π .

n=1

−n

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 1011 / 1411 12 13 14 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
23.02.201534.74 Кб11маркетинг (робота с Ирой).docx
#
12.11.2019365.57 Кб9маркетинг услугТ 1-4.doc
#
23.02.201539.71 Кб5Маркетинг.docx
#
01.05.2019275.97 Кб3Маркетингова географія Л.1.doc
#
23.02.2015173.28 Кб16мат.методы.docx
#
23.02.20151.44 Mб69матан.pdf
#
23.02.20152.78 Mб86Матем. анализ. Методичка(1 семестр).doc
#
13.03.20161.44 Mб37Матеріали до словника 2.doc
#
13.03.2016105.98 Кб4материаловедение Лекция 1.doc
#
25.08.201938.33 Кб4Материалы 3_1.docx
#
10.11.2019241.66 Кб1материалы для лекции 1.doc