матан

Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Харьковский Национальный Университет им. В. Н. Каразина

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

и направлена противоположно движению (скорости v ) FC ↑↑−

.pdf

Скачиваний:

Добавлен:

23.02.2015

Размер:

1.44 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 78 / 148 9 10 11 12 13 14 > Следующая >>>

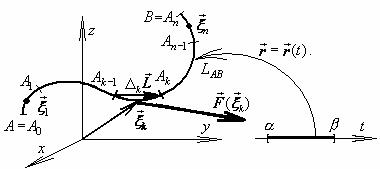
Пусть кривая L находится в силовом непрерывном поле

P(x, y, z)

F (r ) = Q(x, y, z) .

R(x, y, z)

Найдем работу силы F (r ) по перемещению материальной точки из начала A в конецB

кривой LAB .

Разобьем ориентированную кривую LAB на малые

ориентированные части LAk−1Ak , почти совпадающие с вектором

перемещения ∆k r =∆k L = Ak −→1 Ak , и выберем на них промежуточные точки ξk . Тогда работа A равна:

n		n		n
A=∑	∆k A= lim	∑(F (ξk ), ∆k L)=lim		∑P(ξk ,ηk ,ζk )∆k x +Q(ξk ,ηk ,ζk )∆k y + R(ξk ,ηk ,ζk )∆k z
k =1	d →0	k =1	d →0	k =1
k =1		k =1		k =1

Полученный предел называется криволинейным интегралом по координатам от векторфункции F (r ) по ориентированной кривой LAB и обозначается

∫ (F (r ), dr )= ∫ (F (r ), dL)= ∫ P(x, y, z)dx +Q(x, y, z)dy + R(x, y, z)dz .

LAB LAB LAB

Он может быть сведен к следующему определенному:

	β					β
	∫(F (r (t)), rt′(t))dt =∫(P(x(t), y(t), z(t))xt′(t) +Q(...) yt′+ R(...)zt′)dt									.
	α					α
Решения.
№ 38.1.
A= ∫ (F (r ), dL)= ∫ P(x, y, z)dx +Q(x, y, z)dy + R(x, y, z)dz =
LAB		LAB
=[P(x, y, z) = y,		Q(x, y, z) = z,				R(x, y, z) = x]= ∫ (ydx + zdy + xdz)=
						LAB
=[x =ch t,	y =sh t,				z =t;	−1≤t ≤+1]=+∫1	(sh td ch t +td sh t +ch tdt )=
						−1
=+∫1sh2 tdt ++∫1t		ch tdt ++∫1 ch tdt =2+∫1sh2 tdt +0 +2+∫1 ch tdt =2+∫1 ch 22t −1 dt +2+∫1 ch tdt =
−1	−1				−1	0	0	0	0
=(sh22t −t +2sh t )			+1	=(sh22 −1+2sh1).
			+1
			0
			0

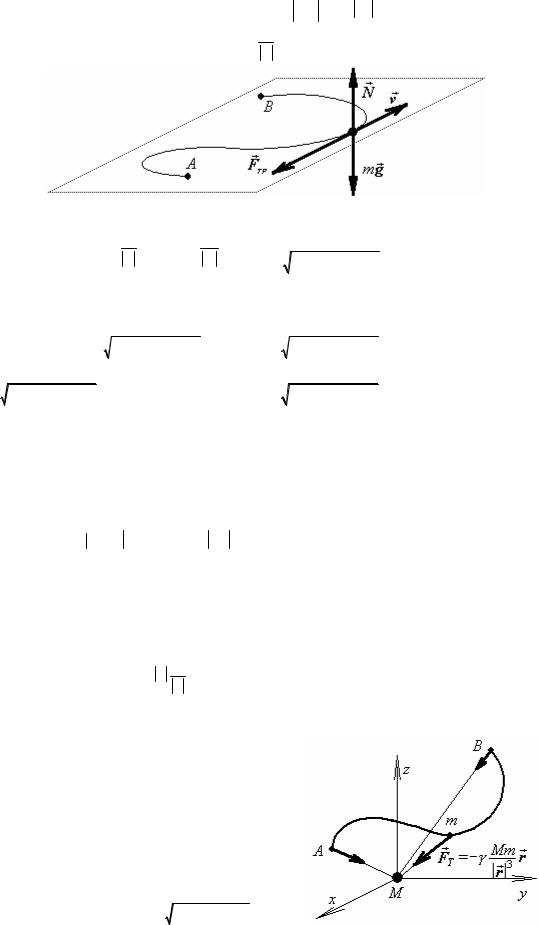
№ 38.2.

Сила трения скольжения FTP по величине равна противоположно движению (скорости v ) FTP ↑↑− vv ,

так что

FTP =−kTP mg vv =−kTP mg rr′′ =−kTP mg

FTP =kTP N =kTP mg и направлена

		1				x′
		1
						y′
x′	2	+ y′	2	+ z′	2	y′
x′		+ y′		+ z′
						z′

Работа силы трения при перемещении материальной точки по плоской кривой равна:

		x′dx + y′dy + z′dz			β	x′2 + y′2 + z′2
A= ∫ (FTP , dL)=−kTP mg ∫					=−kTP mg∫		dt =
A= ∫ (FTP , dL)=−kTP mg ∫			x′2 + y′2 + z′2		=−kTP mg∫	x′2 + y′2 + z′2	dt =
LAB	LAB				α
β					β
=−kTP mg∫	x′2 + y′2 + z′2 dt =−kTP mg L,				где L =∫	x′2 + y′2 + z′2 dt - длина кривой.
α					α
Приведенным преобразованиям можно придать векторную форму записи:
A= ∫ (FTP , dL)= ∫ (−kTP mg			r′	, dL)=−kTP mg ∫ (ф(r ), dL)=
			r′
			r′
LAB	LAB				LAB

= (ф, dL)= фdL cos (ф, dL)= dL =dL =−kTP mg ∫1dL =−kTP mg L.

Замечание. Сила сопротивления воздуха FC по величине пропорциональна величине

x′

FC =−kC v vv =−kC v =−kC r′=−kC y′ .

z′

№ 38.3.

Согласно закону всемирного тяготения (Ньютон, 1687) сила, с которой материальная точка массой M притягивает другую массой m , по величине прямо пропорциональна массам этих точек и обратно пропорциональна квадрату расстояния между ними, и направлена по радиусу-вектору, соединяющего эти точки:

(r )= −γ Mm

=−γ Mm r = −γ

x2 + y2 + z2

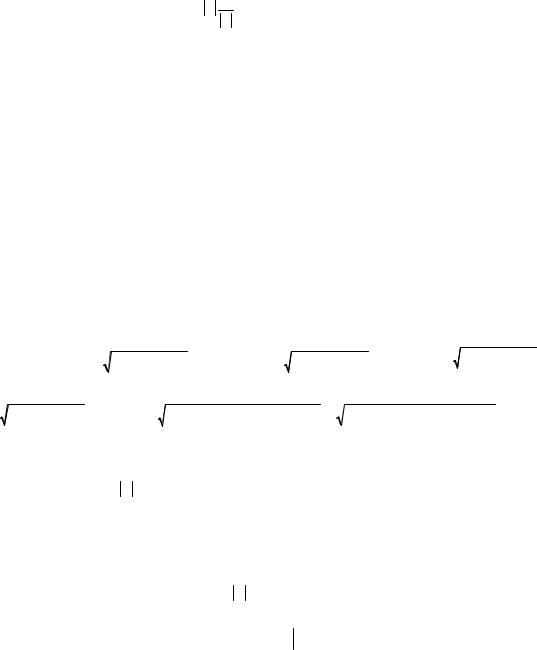
Работа силы тяготения при перемещении материальной точки по кривой материальной точки массой m , находящейся в гравитационном поле FT (r ) . Нетрудно видеть, что

FT (r ) =−grad U (r ) (см. № 27.4). Как видно, работа гравитационного поля не зависит от

кривой, а определяется только ее начальной и конечной точкой, и равна изменению потенциальной энергии точки.

Замечание. Согласно закону Гука (1660) сила упругости Fy равна:

Fy =−ky r

№ 38.4.

Работа векторного поля

F (r )=

x rr =−ky r =−ky y .

u′x grad u(r ) = u′y

u′z

при перемещении материальной точки из начала A в конец B кривой LAB равна:

A= ∫ (F (r ), dr )= ∫ (grad u(r ), dr )=∫ux′ (x, y, z)dx+u′y (x, y, z)dy+uz′(x, y, z)dz=

LAB

равна:

=∫du(x(t), y(t), z(t)) =u(x(t), y(t), z(t))

αβ =u(x(β), y(β), z(β)) −u(x(α), y(α), z(α)).

xdx+ ydy+ zdz

d (x2 + y2 + z2 )

A= ∫ (FT , dr )=−γ Mm∫

2 3

=−γ Mm∫12

=γ Mm∫d

+ y

+ z

+ y

+ z

2 3

+ z

LAB

+ y

=γ Mm

β =γ Mm

−

+ y2 + z2

x2 (β )+ y2 (β )+ z2 (β )

x2 (α)+ y2 (α)+ z2 (α)

Приведенным преобразованиям можно придать векторную форму записи:

A= ∫ (FT , dr )=−γ Mm ∫ (r,rd3r )=−γ Mm ∫ 12

(r,r

)

=−γ Mm ∫ 12 d

=−γ Mm ∫

LAB

=−γ Mm ∫

=γ Mm ∫

(U (B) −U ( A))

=γ Mm

−

=−

r (B)

r (A)

LAB

Mm - это потенциальная энергия

Замечание. Скалярная функция U (r ) =−γ

Приведенным преобразованиям можно придать векторную форму записи:

A= ∫ (F (r ), dr )= ∫ (grad u(r ), dr )= ∫ du(r ) =u(r ) BA =u(B) −u( A).

LAB LAB LAB

Замечание. По аналогии с физическими силовыми полями в математике скалярная функция u(r ) называется потенциалом векторного поля F (r ) = grad u(r ) . Как видно, работа такого поля не зависит от кривой, а определяется только ее начальной и конечной точкой, и равна разности потенциалов. Само векторное поле F (r ) = grad u(r ) называется потенциальным.

39. Поверхностные интегралы по площади (масса, заряд)

Условия.

№ 39 1.			Найти массу поверхности S с поверхностной плотностью ρ = ρ(x, y, z) .
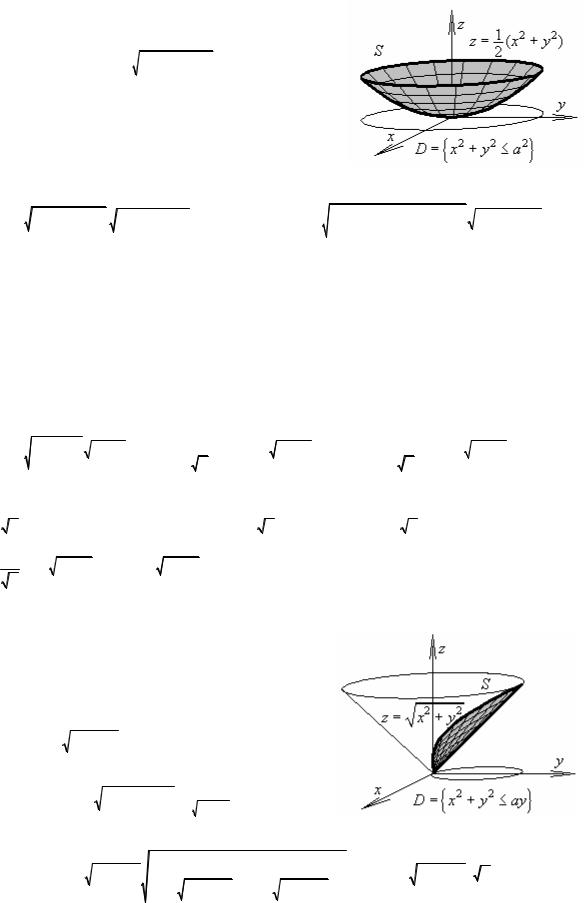
S ={z = 12 (x2 + y2 ), x2 + y2 ≤a2 }						S ={z = x2 + y2 , x2 + y2 ≤ax}
ρ = (x2 + y2 ) z						ρ = (x2 + y2 ) z
№ 39 2.			Найти заряд поверхности S с поверхностной плотностью ρ = ρ(x, y, z) .
S ={z = x2 + y2 ,				x2 + y2 ≤ay}		S ={z = xy, x2 + y2 ≤a2 }
ρ =(x2 + y2 ) z						ρ =(x2 + y2 ) z
№ 39 3.			Найти центр масс поверхности S с			поверхностной плотностью ρ = ρ(x, y, z) .
S ={z = 12 (x2 + y2 ),				x2 + y2 ≤a2 }		S ={z = x2 + y2 ,		x2 + y2 ≤a2 }
ρ =			z			ρ = x2 + y2 z2
	1+ x2 + y2

№ 39 4.			Найти площадь поверхности S .
S ={z =xy, x2 + y2 ≤a2 }						S ={z = 12 (x2 + y2 ),		x2 + y2 ≤a2 }.
№ 39 5.			Найти площадь поверхности S .
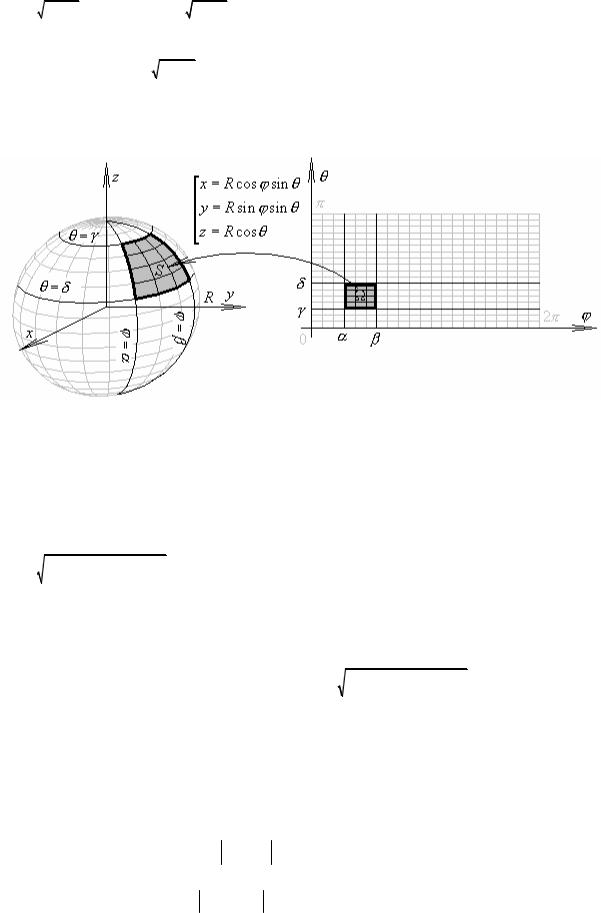
Часть сферы, ограниченной двумя						Часть геликоида
параллелями и двумя меридианами
		x = R cosϕsinθ			,		x = u cos v
S =		y = Rsinϕsinθ				S =	y = u sin v	,
					.


		z = R cosθ					z = v
(ϕ,θ) Ω ={α ≤ϕ ≤ β, γ ≤θ ≤ δ}						(u,v) Ω ={α ≤ u ≤ β, γ ≤ v ≤ δ}

Теория.

Пусть дана простая гладкая поверхность

	x=x(u,v)
S ={r =r (u,v), (u,v) Ω}=	y=y(u,v),(u,v) Ω
	z=z(u,v)

	( непрерывные ru′, rv′, причем [ru′, rv′]≠0) ,

на которой распределена масса (заряд)			с заданной поверхностной непрерывной
плотностью ρ = f (r ) = f (x, y, z) . Найдем массу (заряд) поверхности.
Разобьем поверхность S	на малые части		Sk с	площадью ∆k S и выберем на них
промежуточные точки ξk . Тогда масса m (заряд q ) равна:,
n		n		n
m =∑∆k m = lim		∑ f (ξk )∆k	S = lim	∑ f (ξk ,ηk ,ζk )∆k S
k =1	d →0	k=1	d →0	k =1

Полученный предел называется поверхностным интегралом по площади, от функции f (r ) по поверхности S и обозначается:

∫∫f (r )dS =∫∫f (x, y, z)dS .

S S

Он может быть сведен к следующему двойному:

	∫∫f (r )dS =∫∫f (r (u, v))			[ru′, rv′]		dudv =∫∫ f (r (u, v)) (ru′, ru′)(rv′, rv′)−(ru′, rv′)2 dudv			.


	S	Ω					Ω
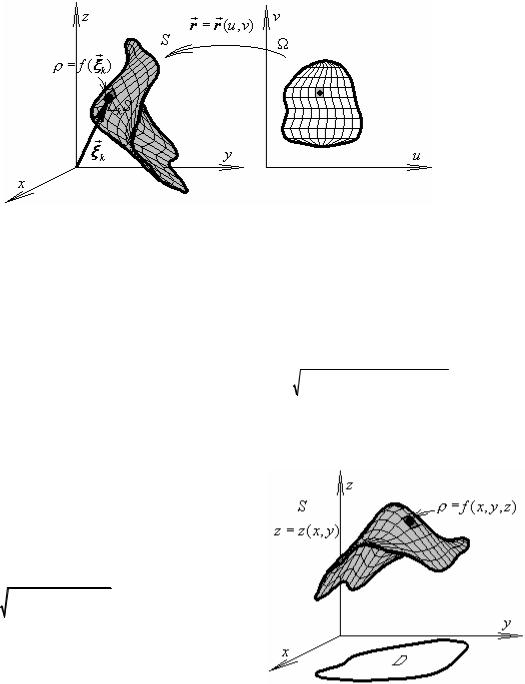
В частном		случае, когда			S ={z = z(x, y), (x, y) D} –			график непрерывно
дифференцируемой функции, интеграл равен:

	∫∫f (x, y, z)dS =
		S
=∫∫f (x, y, z)
=∫∫f (x, y, z)		1+(zx′ )2 +(z′y )2				dxdy
D			z=z(x, y)
D			z=z(x, y)

Решения.

№ 39.1.

m =∫∫ρ(x, y, z)dS =∫∫ (x2 + y2 ) zdS =→

S S

{

}

S =

z = 1 (x2 + y2 ),

(x, y) D =

+ y2 ≤a2

}

→=∫∫

(x2 + y2 ) z

1+ zx′2 + z′y2

z=12( x2 +y2 ) dxdy =∫∫

(x2 + y2 ) 12 (x2 + y2 )

1+ x2 + y2 dxdy =→

Учитывая вид подынтегральной функции

f (x2 + y2 )

и “круговую”

форму области D ,

перейдем к полярным координатам.

Поскольку

x2 + y2 =a2 →r =a ,

то

D ={x2 + y2 ≤a2 } → Ω={r ≤a}={0 ≤ϕ ≤2π, 0 ≤r ≤a}.

Тогда

2∫π (

∫a r2

)dϕ =

2π ∫a r2

→=∫∫

r2 12 r2 1+r2

r drdϕ =

1+r2 r dr

1+r2

r dr =

Ω

1+a2

1+a

π ∫(

(1+r2 )2

−(1+r2 )2 ) d (1+r2 )=

π ∫ (t 2

−t

2 ) dt =

π (52 t

− 32 t 2 )

=π2 52 ( 1+a2 5 −1)− 23 ( 1+a2 3 −1) .

№39.2

q =∫∫ρ(x, y, z)dS =∫∫(x2 + y2 ) zdS =→

S ={z = x2 + y2 ,

(x, y) D ={x2 + y2 ≤ay}}

→=∫∫(x2 + y2 )z

1+ zx′2 + z′y2

z= x2 +y2

dxdy =

=∫∫(x

+ y

)

+ y

dxdy =∫∫

+ y

2dxdy =→

+ y

Учитывая вид подынтегральной функции

f (x2 + y2 )

и “круговую”

форму области D ,

перейдем к полярным координатам.

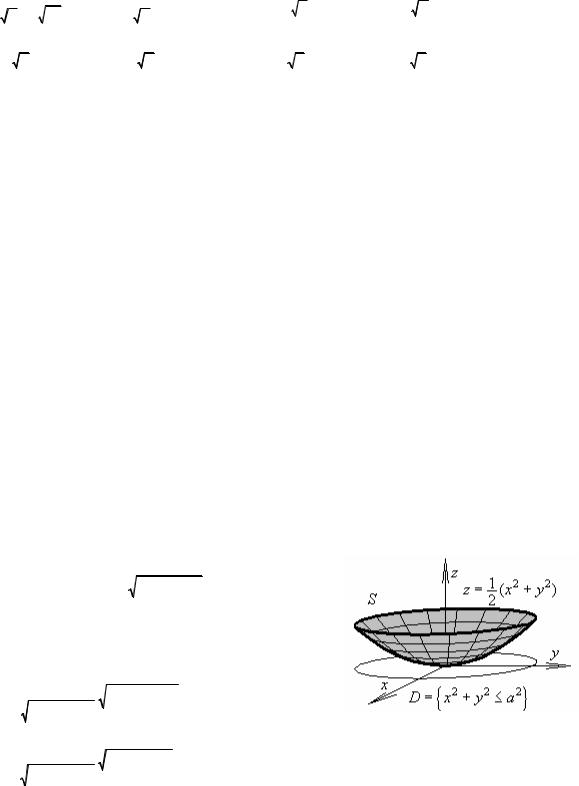
Поскольку

x2 + y2 =ay → r2 =ar sin ϕ r =a sin ϕ,

то

D ={x2 + y2 ≤ay} → Ω={r ≤a sinϕ}={0 ≤ϕ ≤π, 0 ≤r ≤a sinϕ}.

Тогда

→= 2 ∫∫			r2 3 r drdϕ = 2 ∫π (	a sin∫ϕ r4 dr )dϕ =		2		∫π sin5 ϕ dϕ =−	2	∫π (1−cos2 ϕ)2 d cosϕ =
						5			5
	Ω		0	0			0				0
=−	2	−∫1	(1−t2 )2 dt = 252 ∫1	(1−2t2 +t4 ) dt = 252			(1−2 13 + 15 )=16752 .
	5
+1			0
№ 39.3.											S , с поверхностной
При нахождении центра				масс	неоднородной поверхности
плотностью ρ =ρ(r ) =ρ(x, y, z) и массой
				m =∫∫ρ(r )dS =∫∫			ρ(x, y, z)dS
				S		S	,

воспользуемся определением центра масс системы материальных точек. Разобьем

поверхность S

кривыми, на малые, попарно

не налегающие

части Sk с

массами

∆k m ≈ρ(ξk )∆k S =ρ(ξk ,ηk ,ζk )∆k S ,

настолько

малые,

что

каждую

можно

рассматривать как материальную точку ξk =(ξk ,ηk ,ζk ) . Тогда:

= m ∫∫xρ(x, y, z)dS

∫∫r ρ(r )dS

∫∫yρ(x, y, z)dS

r0 ≈

∑ξk ∆k m

≈

∑ξk ρ(ξk )∆k S d→→0

k =1

∫∫zρ(x, y, z)dS

z0 =

Из физических понятий очевидно, что центр масс поверхности с круговой симметрией находится на ее оси: (x0 , y0 , z0 ) = (0,0,?). Цель приведенных ниже расчетов, в частности,

убедиться в адекватности математических формул интуитивным представлениям. Найдем массу поверхности:

m =∫∫ρ(x, y, z)dS =∫∫ 1+ x2 + y2 dS =→
					z
S	{			S					}
	{	2				{			}
S = z = 1			(x2 + y2 ), (x, y) D =			{	x2 + y2	≤a2	}
S = z = 1			(x2 + y2 ), (x, y) D =				x2 + y2	≤a2
→=∫∫ 1+ x2			+ y2	1+ zx′	+ z′y z=12( x2		+y2 ) dxdy =
		z		2	2
D	1
D
=∫∫		(x2 + y2 )		1+ x2 + y2 dxdy = 12 ∫∫(x2 + y2 )dxdy =→
	2
	1+ x2		+ y2
D							D	f (x2 + y2 ) и “круговую” форму области D ,
Учитывая вид подынтегральной функции								f (x2 + y2 ) и “круговую” форму области D ,

перейдем к полярным координатам.

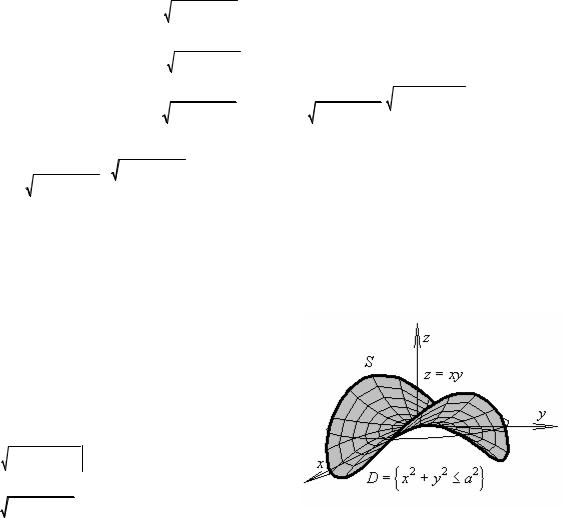
Поскольку

x2 + y2 =a2 →r =a ,

то

D ={x2 + y2 ≤a2 } → Ω={r ≤a}={0 ≤ϕ ≤2π, 0 ≤r ≤a}.

Тогда

→= 2

∫∫r

r drdϕ = 2

2π

(

)dϕ = 2

2π

4 =π

4 .

∫

∫r

Ω

Далее найдем координаты центра масс, учитывая симметрию поверхности относительно координатных плоскостей xOz, yOz и нечетность подынтегральных функций

относительно переменных x, y :

= m ∫∫xρ

(x, y, z)dS = m

∫∫x

1+ x2

+ y2 dS =0,

+ x2

+ y2 dS =0.

= m ∫∫yρ(x, y, z)dS

= m ∫∫y

1+ x2

+ y2

dS = m ∫∫

+ x2 + y2

1+ zx′

+ z′y dxdy =

= m ∫∫zρ(x, y, z)dS = m

∫∫z

(1 (x2 + y2 ))2

∫∫

21+ x2 + y2

1+ x2 + y2 dxdy =

∫∫(x2 + y2 )2 dxdy =

= 4m ∫∫r

2π

)dϕ

= 4m 2π

=π 12m =

3 .

r drdϕ = 4m

∫( ∫r

Ω

№ 39.4.

S =∫∫1 dS =→

S ={z =xy, (x, y) D ={x2 + y2 ≤a2 }}

→=∫∫ 1+ zx′2 + z′y2 z=xy dxdy =

=∫∫ 1+ y2 + x2 dxdy =→

Учитывая вид подынтегральной функции f (x2 + y2 ) и “круговую” форму области D ,

перейдем к полярным координатам. Поскольку

x2 + y2 =a2 →r =a ,

то

D ={x2 + y2 ≤a2 } → Ω={r ≤a}={0 ≤ϕ ≤2π, 0 ≤r ≤a}.

Тогда

								2π		a			a	1
→=∫∫		1+r2 r drdϕ = ∫(								∫				1
→=∫∫		1+r2 r drdϕ = ∫(								∫	1+r2		r dr )dϕ =2π 12 ∫(1+r2 )2 d (1+r2 )=
Ω								0		0			0
	2	(		3	a	2		(			2 3	)
				3	a
			+r	2 )2						+a
=π	3	1			0 =	3	π		1			−1 .
=π		1			0 =		π		1			−1 .

№ 39.5.

Часть сферы, ограниченной двумя параллелями и двумя меридианами:

S =∫∫1 dS =→

cosϕsinθ

S =

r = R sinϕsinθ ,

(ϕ,θ) Ω =

α ≤ϕ ≤ β,

γ ≤θ ≤δ

}

{

cosθ

→=∫∫

rϕ′

rθ′

2 −(rϕ′, rθ′)2 dϕdθ =→

Ω

−sinϕ sinθ

cosϕ cosθ

rϕ′

=R2 sin2 θ,

rθ′

2 =R2 ,

(rϕ′, rθ′)=0

rϕ′ =R

cosϕ sinθ

rθ′ =R

sinϕ cosθ

dS =

rϕ′

rθ′

2 −(rϕ′, rθ′)2 dϕdθ =R2 sinθdϕdθ

−sinθ

→=∫∫R2 sinθdϕdθ =R2 ∫β (		∫δ sinθ dθ	)dϕ =R2 ∫β	1 dϕ ∫δ sinθ dθ=R2 (β −α) (cosγ −cosδ )
Ω	α	γ	α	γ
При α = 0,	β = 2π, γ = 0,	δ =π получаем площадь сферы радиуса R: S =4π R2 .

Сравнить: выражение дифференциала площади сферы радиуса r dS = rϕ′, rθ′ dϕdθ =r2 sinθdϕdθ

с дифференциалом объема при переходе к сферическим координатам dV = (rr′, rϕ′, rθ′) drdϕdθ =r2 sinθdrdϕdθ .

40. Поверхностные интегралы по координатам (поток вектора)

Условия.

№ 40 1. Найти количество жидкости (объем), протекающее в единицу времени через верхнюю сторону поверхности S+ , со скоростью v (r ) .

{ y

S+ = z = xy, x2 + y2 ≤a2 }, v(r ) = z

S+ ={z =x2 + y2 , x2 + y2 ≤a2 }, v(r ) = x

№ 40 2. Найти величину заряда, протекающего в единицу времени через нижнюю сторону поверхности S− , с плотностью заряда ρ(r ) и со скоростью v (r ) .

S− ={z =x2 + y2 , x2 + y2 ≤a2 }	z
	, v(r ) = x
ρ(r ) =x y z	y
ρ(r ) =x y z

S− ={z =x2 + y2 , x2 + y2 ≤a2 }	y
,	v(r ) = z
ρ(r ) =x y z	x
ρ(r ) =x y z

№ 40 3. Найти поток вектора F (r ) через коническую поверхность.

S ={z =a x2 + y2 , (x, y) D}, F (r ) = r .

S ={z =a x2 + y2 ,(x, y) D}, F (r )=

Найти поток вектора F (r ) = r

через поверхность.

№ 40 4.

№ 40.4.

x = u cos v

S+ =

y = u sin v ,(0 ≤ u ≤ a,0 ≤ v ≤ 2π)

S+ =

y = u sin v ,(0

≤ u ≤ a,0 ≤ v ≤ 2π)

= v

№ 40 5.

z = u

№ 40.5.

часть сферы S

=r } площади S .

часть плоскости (r −r0 , n) =0 площади S .

Теория.

Пусть задана простая гладкая поверхность:

x=x(u,v)

rv′, причем [ru′, rv′]≠0) .

S ={r =r (u,v), (u,v)Ω}=

y=y(u,v),(u,v)Ω ( непрерывные ru′,

z=z(u,v)

На ней

можно

выбрать

два непрерывных

поля единичных

векторов нормалей

ru′,rv′

n(r ) =n(r (u, v)) =

(или

−n(r ) ). Тем

самым, определяется

выбор стороны

S+

ru′,rv′

(или S− ) поверхности или, как говорят, ориентации.

Пусть поверхность пронизывает непрерывное векторное поле

P(x, y, z)

F (r ) = Q(x, y, z) .

R(x, y, z)

Например,

F (r ) = v(r ) стационарное поле скоростей жидкости, с плотностью ρ(r ) .

Найдем поток векторного поля F (r ) через заданную сторону S+ (или S− ) поверхности. (Поток v(r ) – это объем, поток ρ(r ) v(r ) – масса жидкости, протекающей через соответствующую сторону в единицу времени).

Разобьем ориентированную поверхность S+ на малые ориентированные части Sk площади ∆k S и выберем на них промежуточные точкиξk ..

<<< < Предыдущая 1 2 3 4 5 6 78 / 148 9 10 11 12 13 14 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
23.02.201534.74 Кб11маркетинг (робота с Ирой).docx
#
12.11.2019365.57 Кб9маркетинг услугТ 1-4.doc
#
23.02.201539.71 Кб5Маркетинг.docx
#
01.05.2019275.97 Кб3Маркетингова географія Л.1.doc
#
23.02.2015173.28 Кб16мат.методы.docx
#
23.02.20151.44 Mб69матан.pdf
#
23.02.20152.78 Mб86Матем. анализ. Методичка(1 семестр).doc
#
13.03.20161.44 Mб37Матеріали до словника 2.doc
#
13.03.2016105.98 Кб4материаловедение Лекция 1.doc
#
25.08.201938.33 Кб4Материалы 3_1.docx
#
10.11.2019241.66 Кб1материалы для лекции 1.doc