Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Харьковский Национальный Университет им. В. Н. Каразина

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

матан

.pdf

Скачиваний:

Добавлен:

23.02.2015

Размер:

1.44 Mб

Скачать

☆

<<< < Предыдущая 1 23 / 143 4 5 6 7 8 9 10 11 12 13 14 > Следующая >>>

№ 29.7.

Необходимо найти функцию z = z(x, y) , являющуюся решением дифференциального

уравнения:

zxx′′ −2zxy′′ + z′′yy =0.

Предлагается

сделать замену

переменных, перейдя от “старых” переменных (x, y) к

новым

(u,v) . Для этого надо найти выражение “старых” производных

z′′

z′′ ,

z′′

через “новые”

′′

z′′

, z′′ .

Поскольку по условию явно выражаются “новые” переменные через “старые”,

u =x + y

= 1 (x2

− y2 )

то рассмотрим сложную функцию от “старых” переменных

z(u(x, y),v(x, y)) = z(x, y) .

Имеем:

zx′ = zu′ ux′ + zv′ vx′ = zu′ 1+ zv′ x = zu′ + xzv′

= z′

u′

+ z′

v′ = z′

1− z′

y = z′ − yz′

z′

(

x ) x

(

v ) x

(

u ) x

(

v ) x

(( u )u

(

u )v )

((

v )u

(

v )v )

+ x

z′′

z′

′

z′

+ xz′

′

z′

′

z′

′

+ z′

z′ ′

z′

′

z′ ′ + x

z′

′

+ z′

((

z′′

(

z′

′

(

z′

+ xz′

′

(

z′

′

+ x

(

z′

′

z′

′ − y

z′

′

+ x

z′ ′

− y

(

z′

′

x )

v ) y

u ) y

v ) y

((

u )u

( u )v )

v )u

v )v )

=(zu′ − yzv′ )′y =(zu′ )′y − y (zv′ )′y − zv′ =((zu′ )′u − y (zu′ )′v )− y ((zv′ )′u − y (zv′ )′v )− zv′

z′′yy =(z′y )′

z′′		= z		+2xz′′	+ x2 z′′		+ z	′
	xx		uu	uv		vv		v
z′′		= z′′		+(x − y)z′′		− xyz′′
	xy		uu		uv		vv
z′′		= z′′		−2 yz′′	+ y	2 z′′	− z′
	yy		uu	uv		vv		v

×1

−

×2

×1

Подставим полученные выражения “старых” производных через “новые” в дифференциальное уравнение:

z′′

−2z′′

+ z′′

=(x2 +2xy + y2 )z′′

=0 u2 z′′

z′′

(z′ )′

z′ =const (u)

z =v const (u)

+const

(u)

z =(x2 − y2 ) f (x + y) + g(x + y)

№ 29.8.

Необходимо найти функцию z = z(x, y) , являющуюся решением дифференциального уравнения:

x2 zxx′′ +2xy zxy′′ + y2 z′′yy =0

Предлагается сделать замену переменных, перейдя от “старых”

переменных (x, y) к

новым

(r,ϕ) . Для этого надо найти выражение “старых”

производных

z′′ ,

z′′

через “новые”

z′′ ,

z′′

z′′ .

rϕ

ϕϕ

Поскольку по условию явно выражаются “старые” переменные через “новые”,

x = r cosϕ

y = r sinϕ

то рассмотрим сложную функцию от “новых” переменных

z(x(r,ϕ), y(r,ϕ)) = z(r,ϕ) .

Имеем:

zr′ =

zx′ cosϕ + z′y sinϕ

z′ =−z′r sinϕ

+ z′r cosϕ

z′′

(z′

)′

cosϕ

(

z′

′

sinϕ

′

cosϕ

zr′′ϕ

(zx′ )ϕ

− zx′ sinϕ +(z′y )ϕ sinϕ + z′y cosϕ

=−(z′ )′

z′ ′

z′′

r sinϕ − z′r cosϕ

(

r cosϕ

− z′r sinϕ

ϕϕ

y )

(

)

(

)

z′′

′′

cosϕ

+ z′′

sinϕ

cosϕ

z′′

cosϕ + z

′′

sinϕ

z′′

(

−z′′ r sinϕ + z′′ r cosϕ

)

cosϕ −z′

sinϕ +

(

−z′′

r sinϕ + z′′

r cosϕ

)

sinϕ + z′

cos

rϕ

z′′

=−

−z′′ r sinϕ + z′′ r cosϕ r sinϕ − z′r cosϕ +

−z′′ r sinϕ + z′′ r cosϕ r cosϕ − z′r sinϕ

(

)

(

)

ϕϕ

z′′

=cos2 ϕ z′′

+2sinϕ cosϕz

′′

+sin2 ϕ z′′

z′′

=−r sinϕ cosϕ z′′

+r (cos2 ϕ −sin2

ϕ)z′′ +r cosϕ sinϕ z′′

−sinϕ z′

+cosϕ z′

rϕ

z′′

=r2 sin2 ϕz′′ −

2r2 cosϕ sinϕ z′′

+r2 cos2 ϕ z′′

−r cosϕ z

′

−r sinϕ z

′

ϕϕ

Получены явные выражения “новых” производных через “старые”. Одновременно эти соотношения можно рассматривать как систему трех уравнений относительно трех неизвестных zxx′′ , zxy′′ , z′′yy , решив которую, найдем выражение “старых” производных

через “новые”. Однако в данном примере можно обойтись без этого, заметив, что производная

r2 zrr′′ =r2 cos2 ϕ zxx′′ +2r cosϕ r sinϕ zxy′′ +r2 sin2 ϕ z′′yy = x2 zxx′′ +2xy zxy′′ + y2 z′′yy

совпадает с левой частью уравнения:

x2 z′′	+2xy z′′	+ y2 z′′	=0 r2 z′′	=0 z′′	=0
xx	xy	yy	rr	rr

(z′ )′

z′ =const (ϕ)

z =r const (ϕ) +const

(ϕ)

z =

+ y

+ g

30. Экстремум функции

Условия.

Исследовать на экстремум функции нескольких переменных.
№ 30.1.	z =−5x2 − y2 +2xy +6x +2 y	№ 30.1.	z =2x2 +5y2 +2xy −10x −12 y
№ 30.2.	z =8x2 −3y2 −2xy −12x +14 y	№ 30.2.	z =3x2 +8y2 +10xy +2x +4 y
№ 30.3.	z =x3 + xy2 −2xy + y2 −11x −2 y	№ 30.3.	z = y3 + x2 y +4xy −x2 −4x −8y
№ 30.4.	u=x2 +y2 +z2 +xy−yz−xz−x−2 y−3z	№ 30.4.	u = x2 + xy + yz − xz −x −4 y − z
№ 30.5.	При каких размерах a) “закрытая”,	b) “открытая” прямоугольная коробка

заданного объема V имеет наименьшую		заданной площади поверхности S имеет
площадь поверхности S .		наибольший объем V .
№30.6.	Найтинаибольшееинаименьшеезначениефункции z = f (x, y) вобласти ϕ(x, y) ≤ 0 .

z =x2 + y2 , x2 +( y −1)2 ≤4		z =x2 − y2 , x2 + y2 ≤1

Теория.

В точке (x ,...)		достигается локальный max
( min )	0
	функции u = f (x,...) , если для
“соседних” точек из некоторой окрестности
(x,...) Uε (x0 ,...) выполнено
	f (x,...) ≤ f (x0 ,...)		∆u ≤ 0 ,
	( f (x,...) ≥ f (x ,...)		∆u ≥ 0).
		0
Если	функция	u = f (x,...) достаточное число раз дифференцируема, то в точке

экстремума с необходимостью первый дифференциал равен нулю du = 0 .

При этом характер экстремума, как этовытекаетизформулы Тейлора,

∆u = du1! + d2!2u +o(dx2 ) ≈ 12 d 2u ,

можно определить, исследуя знак второго дифференциала(достаточное условие)

>0 min

min max .

u = <0

max

В случае

функции

двух

переменных z = f (x, y)

подозрительные на экстремум точки

(x , y ) (стационарные) находятся как решения системы уравнений

fx′(x, y) =0

x = x0

f ′(x, y) =0

y = y

f ′′

A>0 min

, получим AC - B2 =

Полагая,

A<0 max .

f ′′

(x , y )

min max

0 0

В	точке (x , y )			достигается			условный
	0	0
локальный max ( min ) функции							z = f (x, y)
при	условии,	что			ϕ(x, y) = 0 ,		если	для
“соседних” точек из некоторой окрестности
(x, y) Uε (x0 , y0 ) , лежащих на кривой связи,
выполнено
f (x, y) ≤ f (x , y )			,	(	f (x, y) ≥ f (x , y )			)
	0	0	,	(		=0	0 0	)
ϕ(x, y) =0					ϕ(x, y)	=0
Если функции					.	достаточное число раз дифференцируемы, то в точке
Если функции		f (x, y),			ϕ(x, y)	достаточное число раз дифференцируемы, то в точке
экстремума с необходимостью равен нулю первый дифференциал функции Лагранжа
									Fx′= fx′−λϕx′ =0
	F(x, y;λ) = f (x, y) −λϕ(x, y) dF =0								F ′ = f ′ −λϕ′ =0 .
									y y	y

									Fλ′ =−ϕ =0

Решения.

№ 30.1.

z =−5x2 − y2 +2xy +6x +2 y .

Найдем “подозрительные” на экстремум точки (необходимое условие экстремума):

zx′ =−10x +2 y +6 =0			−5x + y =−3	x0 =1
z′	=−2 y +2x +2	=0	x − y =−1	y	0	=2
y					0

Выясним характер экстремума (достаточное условие экстремума):

z′′xx =(−10x +2 y +6)′x =−10= A
z′′xy =(−10x +2 y +6)′y = 2 =B AC - B2 =(−10)(−2)−22 =16>0, A=−10<0 max

z′′yy =(−2 y +2x +2)′	y	=−2 =C

№ 30.2.

z =8x2 −3y2 −2xy −12x +14 y

Найдем “подозрительные” на экстремум точки (необходимое условие экстремума):

z′	= 16x − 2 y −12 = 0	8x − y = 6	x =1
x			0
z′y = −6 y − 2x +14 = 0		x + 3y = 7	y0 = 2

Выясним характер экстремума (достаточное условие экстремума):

z′′

= 16x −2 y −12

′

=16 = A

(

)

(

)

(

)

(

)

2 =−100

z′′

= 16x −2 y −12

′

=−2 =B AC - B2 =16

−6

−

−2

minmax

z′′yy =(−6 y −2x +14)′

=−6 =C

№ 30.3.

z =x3 + xy2 −2xy + y2 −11x −2 y

Найдем “подозрительные” на экстремум точки (необходимое условие экстремума):

zx′	=3x2 + y2 −2 y −11=0		y2	−2 y +3x2 −11=0		2	−2 y +3x	2	−11=0
zx′	=3x2 + y2 −2 y −11=0		y2	−2 y +3x2 −11=0	y		−2 y +3x		−11=0
		=0		+1)(y −1)=0	x =−1
z′y =2xy −2x +2 y −2		=0	(x	+1)(y −1)=0

					y =1

−2 y +3x

−11=0

=−1

x1 =−1

x2 =−1

1, 2)

1,2

=−1

−2 y −8 =0

=−2

=+4

x1,2

3, 4)

y2 −2 y +3x2 −11=0

3x2 −12 =0

x3 =−2

x4 =+2

=+1

3,4

Выясним характер экстремума (достаточное условие экстремума):

z′′

(

3x2 + y

2 −2 y

−11

′

=6x

(

′

z′′

3x2 + y

2 −2 y

−11

=2 y −2

)

z′′yy =(2xy −2x +2 y −2)′y

=2x +2

=−6

A=6x

(−1,−2)

B =(2 y −2)

(−1,−2) =−6

AC - B2 =(−6)0 −(−6)2 =−36 <0

minmax

= 0

C =(2x +2)

(−1,−2)

=−6

=6x

(−1,+4)

B =(2 y −2)

(−1,+4) =+6

AC - B2 =(−6)0 −(+6)2 =−36 <0

minmax

=(2x +2)

= 0

(−1,+4)

=6x

−2,+1

=−12

(

)

B =(2 y −2)

(−2,+1) =0

AC - B2 =(−12)(−2)−02 =24 >0,

A =−12 <0

max

=(2x +2)

=−2

(−2,+1)

=6x

+2,+1

=+12

(

)

B =(2y −2)

(+2,+1) =0

AC - B2 =(+12)(+6)−02 =72 >0,

A =+12 >0

min

=(2x +2)

=+6

(+2,+1)

№ 30.4.

u = x2 + y2 + z2 + xy − yz − xz − x −2 y −3z

Найдем “подозрительные” на экстремум точки (необходимое условие экстремума):

	ux′			ux′ =2x + y − z −1=0												2x +y −z =1
U ′= u′		=0		u′	=2 y + x − z −2 =0										x +2 y −z =2
	y			y												−x −y +2z =3
																−x −y +2z =3
	uz′			uz′ =2z − y − x −3=0
	2 1 −1		1		1		2 −1					2		1	2 −1				2
	2 1 −1		1		1		2 −1					2		1	2 −1				2
		−1	2				1 −1					1			−3 1				−3
	1 2	−1	2		2		1 −1					1		0	−3 1				−3
	−1 −1 2		3		−1	−1 2						3		0	1	1	5
	−1 −1 2		3		−1	−1 2						3		0	1	1	5
					1		2 −1				2		1		0 −3				−8
					1		2 −1				2		1		0 −3				−8
					0	1		1			5			0	1 1				5
					0	1		1			5			0	1 1				5
					0									0	0 4				12
					0	−3 1					−3			0	0 4				12
						−3 1					−3									x0 =1
				1			0 −3			−8			1		0	0		1
				1			0 −3			−8			1		0	0		1
					0	1 1				5				0	1	0		2			=2
					0	1 1				5				0	1	0		2		y0	=2
					0	0			1	3				0	0	1		3
									1

																				z0	=3

Выясним характер экстремума (достаточное условие экстремума):

′′

−1

uxx

uxy

uxz

U ′′= u′′

u′′

0 U ′′

1 2

−1

u′′

(1,2,3)

−1 −1

∆1 =

=2>0,

∆2 =

3>0,

−1

1 2 −1

∆3 =

1 2

−1

=−

2 1 −1

=−

0 −3 1

0 1 1

=4 >0

−1 −1 2

0 1 1

0 −3 1

0 0 4

min

№ 30.5.

a) Учитывая симметрию “закрытой” коробки

относительно размеров x, y, z , из

геометрических соображений, очевидно, что наименьшую площадь поверхности имеет кубическая коробка:

x = y =z V =x y z x = y =z =3 V Smin =2(x y + y z + z x)=63 V 2 ,

а наибольшую S = ∞ – “плоская” коробка. Например:

	V		S =2(x y + y z + z x)=2		V		V
x = y →∞, z =		→0		x y + y		+		x	→∞ .
	x y				x y		x y

Проверим адекватность математического аппарата интуитивным представлениям. Имеем:

S = f (x, y, z) =2(x y + y z + z x)→min

ϕ(x, y, z) = x y z −V =0

F(x, y, z;λ) = f (x, y, z) −λϕ(x, y, z) =2(xy + yz + zx)−λ(xyz −V )

Найдем “подозрительные” на условный экстремум точки (необходимое условие условного экстремума):

Fx′= fx′−λϕx′ =2( y + z) −λyz =0

2( y + z) −λyz =0

2( y − x) −λz( y − x) =0

F ′

= f

′ −λϕ′

=2(z + x) −λzx =0

− y) −λx(z

− y) =0

2(z + x) −λzx =0

2(z

F ′= f

′−λϕ′ =2(x + y) −λxy =0

2(x

−λ

2(x

−

−λ

y(x

−

Fλ′

−ϕ =−(xyz −V )

xyz =V

( y − x)(2 −λz) =0

(z − y)(2 −λx) =0

x = y = z

x = y

= z

=3 V

(x − z)(2 −λy) =0

xyz =V

Пусть

для определенности

коробка

“открыта

сверху”.

Из геометрических

соображений, очевидно, что x= y>0,

z >0,

так что

V =x y z =x2 z ,

S =x y +2(y z + z x)=x2 +4xz.

Имеем:

+4xz →min

S = f (x, z) =x

ϕ(x, z) =x2 z −V =0

F(x, z;λ) = f (x, z) −λϕ(x, z) =(x2 +4xz) −λ(x2 z −V )

Найдем “подозрительные” на условный экстремум точки (необходимое условие условного экстремума):

F ′

= f ′−λϕ′

=2x +4z −2λxz =0

+2z −λxz =0

= f ′−λϕ′

=4x

−λx2 =0

x(4

−λx) =0

F ′

= −ϕ =−(x

z −V )=0

Fλ′

+(2

−λ

z =

x =

z =V

(λ )

		+(2 −λx)z =0
	x	+(2 −λx)z =0
				4
		= λ
x		= λ
		2	z =V
	x		z =V
=	2					z =	1 3		2V
	λ					z =	2		2V
	λ						2
	4						3
=					x =			2V
=	λ				x =			2V
3 = 32								32
3 = 32					λ =3			32
	V							V

Итак, x = y	0	=3	2V ,	z	0	= 1	3 2V S	min	=	1	63 V 2 .

0						2			3 2

Тот факт, что в найденной точке достигается именно min , вытекает из геометрических соображений.

Сравнить с a)

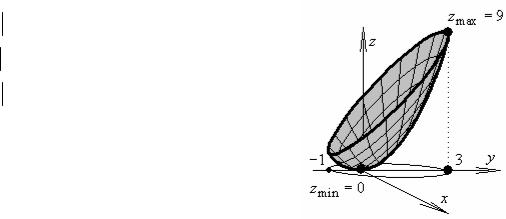
№ 30.6.

Найдем “подозрительные” на экстремум функции z =x2 + y2 точки, находящиеся внутри области x2 +( y −1)2 <4 (необходимое условие безусловного экстремума):

zx′ =2x =0		x0 =0
z′	=2 y =0	y	0	=0
y

Очевидно, найденная точка лежит внутри области: x02 +( y0 −1)2 =02 +(0 −1)2 =1<4.

Найдем далее “подозрительные” на экстремум функции z =x2 + y2 точки, находящиеся на границе x2 +( y −1)2 =4 области (необходимое условие условного экстремума):

f (x, y) = x2 + y2 →extr

ϕ(x, y) = x2 +( y −1)2 −4 =0

F(x, y;λ) = f (x, y) −λϕ(x, y) = x2 + y2 −λ(x2 +( y −1)2 −4)

x(1−λ) =0

Fx′=2x −2λx =0

x =0

F ′ =2 y −2λ( y −1) =0

y(1−λ) =−λ

+( y

−4)=0

Fλ′ =−(x2

+( y −1)2

+( y −1)

Вычислим функцию во всех подозрительных точках:

z0 =x2 + y2 (0,0) =0,

z1 =x2 + y2 (0,−1) =1,

z2 =x2 + y2 (0,3) =9.

zmin =0 достигается внутри области в точке (0,0) : zmax =9 достигается на границе области в точке (0,3) .

				x1 =0		x2 =0
−	1)	2 =	4	y	=−1,	y	2	=3
	1)		4	1			2

31. Элементы дифференциальной геометрии

Условия.

№ 31.1. Траектория движения точки описывается заданными параметрическими уравнениями. Найти величину и направление скорости движения. Написать уравнение касательной прямой и нормальной плоскости к кривой в заданный момент времени.

x =a cos t	(0	≤t ≤2π ), t		= 1		x =a t cos t	(0	≤t ≤2π ), t		= 1
y =a sin t ,	(0	≤t ≤2π ), t	0	= 1	π	y =a t sin t ,	(0	≤t ≤2π ), t	0	= 1	π
z =t			0	3		z =t			0	6

№ 31.2. Написать уравнение касательной прямой и нормальной плоскости к кривой, как линии пересечения двух поверхностей, заданных явно.


z = x2		+ y2	, (x , y , z	0	) =(2,	−2, +8)	z = xy		(x0 , y0 , z0 ) =(2,3, 6)
	−2x −4 y		0 0	0			z =1	+ x + y
z =4	−2x −4 y

№ 31.3. Написать уравнение касательной прямой и нормальной плоскости к кривой, как линии пересечения двух поверхностей, заданных неявно.

+ y 2

+z2

=50, (x , y , z

) =(3, 4,5)

+ y 2

−z2 =4 , (x , y , z

) =(1, 2,1)

+ y

−z

0 0

+ y

−5z =0

0 0

№ 31.4. Построить поверхность, заданную параметрически, и координатные линии. Написать уравнения касательных прямых к координатным линиям, касательной плоскости и нормальной прямой к поверхности.

x =u cos v

0 ≤u ≤a

(u0 , v0 ) =(1 a, 1

π )

x =u cos v

≤u ≤a

, (u0

, v0 )

1 a, 1

π )

y =u sin v ,

≤v ≤2π

0 ≤v ≤2π

2 6

3 3

z =v

z =u

№ 31.5. Написать уравнения касательной плоскости и нормальной прямой к

поверхности, заданной явно.

z = xy, (x0 , y0 , z0 ) =(−1, −2, 2)

z = x2 + y2 ,

(x , y

, z

) =(−1, +2,5)

№ 31.6. Написать уравнения касательной плоскости к поверхности, заданной неявно.

y 2

−

=1, (x , y

, z

)

y 2

=1, (x , y

, z

)

Теория.

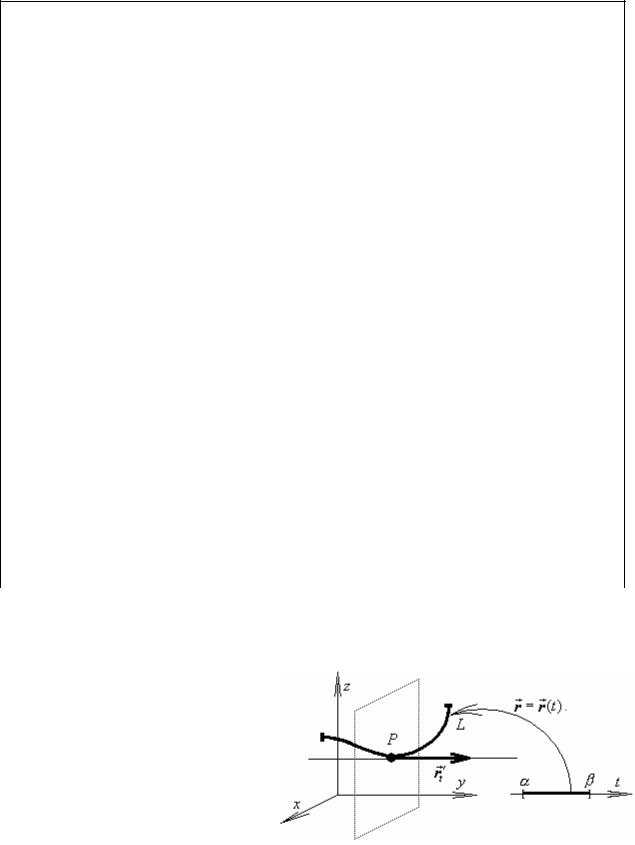
Простой кривой называется образ L непрерывного взаимно однозначного отображения r = r (t) отрезка [α, β] R1 в пространство R3

		x = x(t)
L ={r =r (t), t [α, β]}={		y = y(t), t [α, β] }.

		z = z(t)
Кривая называется	гладкой, если
′		′
непрерывная rt (t) , причем rt (t) ≠ 0 .
Такое название объясняется тем, что
в каждой точке P		касательная
прямая к кривой, а значит, кривая не
имеет изломов.		кривой проходит через точку P , параллельно вектору rt′.
Касательная прямая	к	кривой проходит через точку P , параллельно вектору rt′.

Плоскость, проходящая через точку P ортогонально к касательной прямой, называется нормальной плоскостью к кривой.

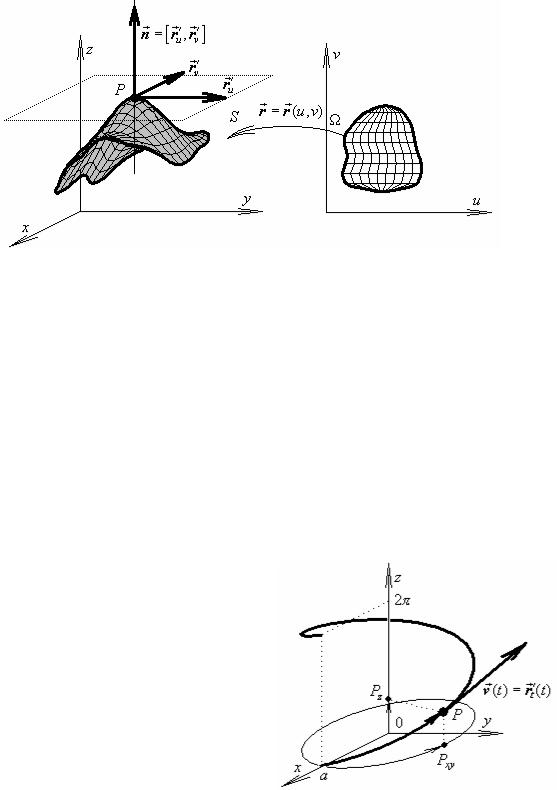
Простой поверхностью	называется образ	S –	непрерывного взаимно однозначного
отображения r = r (u,v)	замкнутой области Ω R2		в пространство R3
		x = x(u, v)
S ={r =r (u, v), (u, v) Ω}={		y = y(u, v), (u, v) Ω }.

		z = z(u, v)

Поверхность называется гладкой, если непрерывные ru′, rv′, причем [ru′, rv′]≠0 .

Такое название объясняется тем, что в каждой точке P – касательная плоскость к поверхности, а значит, поверхность не имеет изломов.

Касательная плоскость к поверхности проходит через точку P , параллельно векторам ru′, rv′, т.е. ортогонально вектору n =[ru′, rv′]. Прямая, проходящая через точку P

ортогонально касательной плоскости, т.е. параллельно вектору n =[ru′, rv′], называется нормальной прямой к поверхности.

Решения.

№ 31.1.
Проекция	Pxy	точки	P		на	плоскость	xOy
движется	по окружности					x =a cos t
движется	по окружности					y =a sin t ,

(0 ≤ t ≤ 2π )	радиуса		a	с	центром в начале
координат,	а	проекция		Pz	равномерно		z = t

движется по оси Oz , “распрямляя” окружность в виток винтовой линии.

<<< < Предыдущая 1 23 / 143 4 5 6 7 8 9 10 11 12 13 14 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
23.02.201534.74 Кб11маркетинг (робота с Ирой).docx
#
12.11.2019365.57 Кб9маркетинг услугТ 1-4.doc
#
23.02.201539.71 Кб5Маркетинг.docx
#
01.05.2019275.97 Кб3Маркетингова географія Л.1.doc
#
23.02.2015173.28 Кб16мат.методы.docx
#
23.02.20151.44 Mб69матан.pdf
#
23.02.20152.78 Mб86Матем. анализ. Методичка(1 семестр).doc
#
13.03.20161.44 Mб37Матеріали до словника 2.doc
#
13.03.2016105.98 Кб4материаловедение Лекция 1.doc
#
25.08.201938.33 Кб4Материалы 3_1.docx
#
10.11.2019241.66 Кб1материалы для лекции 1.doc