
матан
.pdfЗамечание. Положим x =π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
)sin n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
π |
1 |
∞ |
n |
( |
|
1 |
|
|
|
|
|
|
1 |
π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
sinα 2 |
=π sinαπ ∑(−1) |
|
|
|
− |
|
|
|
2 = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
α −n |
α +n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
n=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( |
|
|
|
|
|
|
|
|
|
)(−1) |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
π |
|
|
|
π |
∞ |
|
|
2m+1 |
|
1 |
|
|
|
|
|
1 |
|
m |
|
||||||||||
|
|
|
|
|
|
|
|
|
=π |
|
2sinα 2 cosα 2 |
∑(−1) |
|
|
|
|
|
|
|
− |
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
α −(2m +1) |
α +(2m +1) |
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m=0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
1 |
2 |
∞ |
m |
|
1 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
∞ |
|
|
|
|
m |
|
|
|
1 |
|
|
|
|
|
1 |
|
|
|
|
||||||||
|
|
=π |
∑(−1) |
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
= ∑ |
(−1) |
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
||||
|
cos πα |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
πα −(mπ +π ) |
||||||||||||||||||
|
|
m=0 |
α +(2m +1) |
|
|
α −(2m +1) |
m=0 |
|
|
|
|
|
|
|
|
|
πα +(mπ +π ) |
|
||||||||||||||||||||||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
2 |
|
|
2 |
2 |
|
|
|
|||
Обозначая через z |
=πα |
, получим разложение функции |
|
|
|
1 |
на простые дроби |
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
cos z |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
2 |
|
|
|
|
|
|
|
∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
= ∑(−1)m |
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
) |
|
|
|
|
(2 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
cos z |
|
m=0 |
|
|
|
|
(2 |
|
|
|
z |
− |
|
) |
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
z + |
π +mπ |
|
|
|
|
|
π +mπ |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
zm =± |
(2 |
|
|
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
по корням знаменателя: |
|
|
π +mπ |
|
|
(m =0, 1, |
2,...) . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
Замечание. Полученное представление является аналогом разложения рациональной дроби в сумму простых дробей по корням знаменателя.

46. Ряды Фурье по Cos и по Sin
Условия.
Разложить функцию в ряд Фурье. Построить график суммы ряда Фурье. Полагая что: x = 0 , x =π2 , x =π , найти суммы получающихся числовых рядов.
№ 46.1. |
f (x) = x2 |
|
№ 46.1. |
f (x) = x3 |
|
a) −π ≤ x ≤ +π, b) 0 ≤ x ≤ 2π |
|
|
a) −π ≤ x ≤ +π, b) 0 ≤ x ≤ 2π |
Разложить функцию в ряд Фурье. Построить |
график ряда Фурье. |
|||
№ 46.2. |
f (x) = x2 |
|
№ 46.2. |
f (x) = x3 |
|
a) −l ≤ x ≤ +l, b) 0 ≤ x ≤ 2l |
|
|
a) −l ≤ x ≤ +l, b) 0 ≤ x ≤ 2l |
|
|
|
|
|
Разложить функцию в ряд Фурье по |
Cos и по |
Sin .. Построить графики сумм |
||
полученных рядов. |
|
|
|
|
№ 46.3. |
f (x) = x2 |
|
№ 46.3. |
f (x) = x3 |
|
a) 0 ≤ x ≤π, b) 0 ≤ x ≤ l |
|
|
a) 0 ≤ x ≤π, b) 0 ≤ x ≤ l |
|
|
|
|
|
Теория.
Пусть функция |
y = f (x) кусочно-непрерывно дифференцируемая в интервале длиной 2l |
||||||||||||||||||||
(например, |
[−l, +l] , |
[0,2l], [a,b]=[a, a +2l], |
l =b −a ), |
|
причем точки |
разрыва |
x |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
0 |
|
регулярны |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
f (x0 +0) + f (x0 −0) |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
f (x0 ) = |
|
. |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
1 x ≤+1 |
|
|
|
|
|
|
||||
Интервал |
−l ≤ x ≤ +l |
“сожмем” |
в l раз |
−1≤ |
и “растянем” |
” в |
π |
раз |
|||||||||||||
−π ≤π x ≤+π |
|
|
|
|
|
|
|
|
|
|
l |
|
π x = y x = |
l |
|
|
|
||||
(т.е. |
|
сделаем |
замену |
переменной |
|
y |
|
||||||||||||||
|
|||||||||||||||||||||
l |
x)= f (x) = f ( |
|
y)). Разложив функцию |
|
|
|
l |
π |
|
|
|||||||||||
g( y) = g (πl |
l |
g( y) в ряд Фурье на “привычном” |
|||||||||||||||||||
π |
|||||||||||||||||||||
интервале −π ≤ y ≤ +π , после замены переменной получим разложение f (x) |
на заданном |
||||||||||||||||||||
интервале |
−l ≤ x ≤ +l |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
a0 |
|
∞ |
|
πl x +bn sin n πl x). |
|
|
|
|
|
||||||
|
|
|
|
f (x) = |
+∑(an cos n |
|
|
|
|
|
|||||||||||
|
|
|
|
2 |
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
n=1 |
|
|
|
|
|
|
|
|
|
|
|
||
Это разложение можно получить, вычисляя непосредственно коэффициенты по формулам:
1 |
+l |
f (x) cos n |
π |
xdx, |
n =0, 1, 2,... |
1 |
+l |
f (x)sin n |
π |
xdx, |
n = 1, 2,... |
an = l |
∫ |
l |
bn = l |
∫ |
l |
||||||
|
−l |
|
|
|
|
|
−l |
|
|
|
|
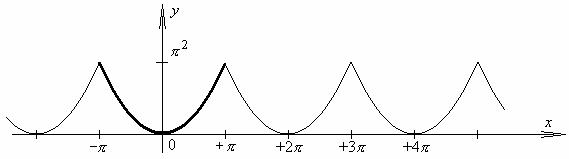
Решения.
№ 46.1.
a) f (x) = x2 , −π ≤ x ≤+π .
Найдем коэффициенты ряда Фурье: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
Функция f (x) = x2 |
|
– четная на интервале [−π, +π ] |
|
b |
= 0. |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
2 |
π |
|
2 π |
2 |
|
|
|
|
2 x3 |
|
π |
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
a0 = |
|
|
∫ |
f (x)dx = |
|
|
∫x |
|
dx |
= |
|
|
|
|
|
|
0 = |
3 π |
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
π |
π |
|
π |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
0 |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
an = 2 |
π |
f (x) cos nxdx = |
2 |
π |
x2 |
cos nxdx = |
|
2 |
π |
x2 d sin nx = |
|
|
|
|
π |
− |
π |
sin nxdx2 |
|
= |
||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
∫ |
∫ |
|
∫ |
|
2 x2 sin nx |
|
∫ |
|
||||||||||||||||||||||||||||||||||
|
|
π |
|
|
|
|
|
|
π |
|
|
|
|
|
|
|
|
|
|
|
πn |
|
|
|
|
|
πn |
|
|
0 |
|
|
|
|
||||||||
|
|
|
|
0 |
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
=− 4 |
π |
x sin nxdx = |
|
4 |
|
π |
xd cos nx = |
4 |
|
x cos nx |
|
π |
− |
π cos nxdx |
= |
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
πn ∫ |
|
|
|
πn2 |
∫ |
|
|
|
|
|
|
|
|
|
|
πn2 |
|
|
|
0 |
|
∫ |
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
0 |
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
1 |
|
|
|
|
|
π |
4 |
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
= |
|
|
(π cos nπ − n sin nx |
|
0 )= |
|
(−1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
πn2 |
|
n2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
Итак, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 =π 2 +4∑ |
(−1)2 |
cos nx, |
|
|
|
−π ≤ x ≤+π |
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
n=1 |
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Используя полученное разложение, с учетом вида (непрерывности) графика суммы ряда Фурье, найдем суммы некоторых числовых рядов:
x = 0 |
|
|
n |
|
|
|
|
n |
|
|
|
|
|
|
n+1 |
|
|
0 =π 2 |
|
∞ |
|
|
∞ |
|
|
|
|
∞ |
|
|
|
||||
+4∑(−1)2 cos n0 =π 2 +4∑ |
(−1)2 |
|
|
|
∑ |
(−1)2 |
=π 2 |
; |
|||||||||
3 |
|
n=1 |
n |
3 |
|
n=1 |
n |
|
|
|
|
n=1 |
|
n |
12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
x =π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
n |
|
|
|
|
|
2m |
|
|
|
|
m+1 |
|
|
|
|
|
∞ |
|
|
|
∞ |
(−1) |
|
∞ |
|
|
|
|
||||
π 2 =π 2 |
+4∑ |
(−1)2 |
cos n π =π 2 |
+4∑ |
|
(−1)m |
|
∑ |
(−1)2 |
=π 2 |
; |
||||||
|
2 |
||||||||||||||||
4 |
3 |
n=1 |
n |
2 3 |
|
|
m=1 |
(2m) |
|
m=1 |
|
m |
12 |
|
|||
x =π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∞ |
n |
|
|
|
∞ |
n |
|
|
|
∞ |
1 |
|
|
|
|
π 2 =π 2 |
+4∑ |
(−1)2 |
cos nπ =π 2 |
+4∑(−1)2 |
(−1)n |
|
∑ |
=π 2 . |
|
|
|||||||
2 |
|
|
|||||||||||||||
3 |
n=1 |
n |
3 |
|
n=1 |
n |
|
|
|
n=1 |
n |
6 |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
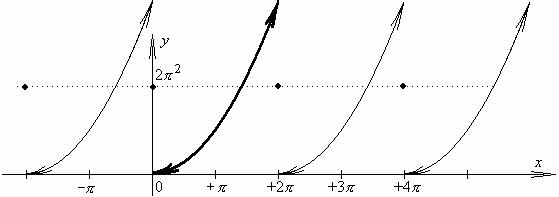
b) f (x) = x2 , 0 ≤ x ≤2π .
|
1 |
|
2π |
|
|
|
|
|
|
1 |
2π |
|
2 |
|
|
1 x3 |
|
2π |
|
|
8 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
a0 = |
|
|
∫ |
f (x)dx = |
|
|
∫ |
x |
|
dx = |
|
|
|
|
|
|
0 |
|
= |
3π |
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
π |
|
π |
|
|
π |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
0 |
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
1 |
2π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
∫ |
f (x)cos nxdx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
an =π |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
2π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
2π |
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∫ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∫ |
f (x)e |
−inx |
dx= |
|
|
|||||
|
1 |
2π |
|
|
|
|
|
|
|
|
|
|
|
an −ibn =π |
|
f (x)(cos nx−isin nx)dx=π |
|
|
|
|||||||||||||||||||||||||||||||||||||
∫ |
f (x)sin nxdx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
||||||||||||
bn |
=π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
=1 |
2π |
x2e−inxdx=− |
|
1 |
2π |
x2de−inx =− |
1 |
|
|
|
|
|
|
2π |
|
|
2π |
|
e−inxdx2 |
|
|
1 |
|
|
|
2π −2 |
2π |
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
∫ |
|
|
∫ |
x2 e−inx |
|
− |
∫ |
|
=− |
|
|
4π 2 e−in |
∫ |
xe−inxdx = |
||||||||||||||||||||||||||||||||||||||||||
π |
|
|
|
|
|
|
|
|
πin |
|
|
|
|
|
|
|
|
|
|
πin |
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
πin |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
||
|
1 |
|
|
|
|
1 |
|
|
2π |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
2π |
|
2π |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
=− |
|
4π 2 +2 |
|
|
|
∫ |
xde−inx =− |
|
|
|
4π |
2 +2 |
|
x e−inx |
|
|
|
|
− |
∫ |
e−inxdx |
|
= |
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
πin |
|
|
in |
|
|
|
|
|
|
|
πin |
|
|
|
|
|
|
in |
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
||
=−π1in (4π 2 +2 |
1 |
(2π e−in2π −0))=−π1in (4π 2 +4inπ )=− |
1 |
(4π+ |
4 |
)=i 4nπ + |
4 |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
in |
in |
in |
n2 |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a −ib = |
|
|
|
4 |
|
+i 4π |
|
|
a = |
4 |
, b =− |
4π |
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n2 |
|
|
n2 |
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
n |
|
|
|
|
|
|
n |
|
|
|
|
|
n |
|
|
|
|
n |
|
n |
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Итак, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
x2 = 4π 2 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
1 sin nx, |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
+4∑ |
|
|
cos nx −4π∑ |
|
|
0 |
< x <2π . |
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
n2 |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
n=1 |
|
|
|
|
|
|
|
|
n=1 |
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Используя полученное разложение, с учетом вида графика суммы ряда Фурье, из которого видно к чему сходится ряд в точках разрыва, найдем суммы некоторых числовых рядов.
x = 0 |
|
|
|
|
∞ |
|
|
|
|
|
|
|
∞ |
|
|
|
|
|
|
|
|
∞ |
|
|
|
|
|
|
∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
4π |
2 |
|
|
1 |
|
|
|
1 sin n0 |
= 4π 2 |
1 |
|
|
|
|
|
1 |
|
=π 2 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||
2π 2 = |
+ |
4∑ |
cos n0 −4π∑ |
+4∑ |
|
|
∑ |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
n2 |
n2 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
3 |
|
|
n=1 |
n2 |
|
|
n=1 |
n |
|
|
|
|
|
3 |
n=1 |
|
|
|
|
n=1 |
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
x =π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
∞ |
|
|
|
|
|
|
|
∞ |
|
|
|
|
|
|
|
|
∞ |
|
|
|
|
|
|
|
|
|
|
|
∞ |
|
|
|
|
|
|
|
|
|
||
π 2 = |
4π |
2 |
|
|
1 |
|
cos n π |
|
1 sin n |
π |
= 4π 2 |
|
1 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
||||||||||||||||
+4∑ |
|
|
−4π ∑ |
+4∑ |
|
|
|
(−1)m |
−4π ∑ |
|
|
|
(−1)m |
|
|
|||||||||||||||||||||||||||||||
|
|
|
(2m)2 |
2m+1 |
|
|
||||||||||||||||||||||||||||||||||||||||
4 |
|
3 |
|
|
|
n=1 n2 |
2 |
|
n=1 n |
|
|
|
2 |
3 |
m=1 |
|
|
|
|
|
|
|
m=0 |
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
∞ |
(−1)2 |
m |
∞ |
|
|
m |
=−13π |
2 |
|
|
|
∞ |
|
m+1 |
|
|
|
2 |
|
|
∞ |
|
|
m |
=π |
|
|||||||||
|
|
|
|
|
|
∑ |
− |
4π ∑ |
(−1) |
|
|
|
cp. |
∑ |
(−1)2 |
|
|
= |
π |
|
, |
∑ |
(−1) |
|
|
|||||||||||||||||||||
x =π |
|
|
|
|
|
|
|
m=1 |
m |
|
m=0 |
2m+1 |
|
12 |
|
|
|
|
m=1 |
m |
|
|
|
|
12 |
|
|
m=0 |
2m+1 |
4 |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
∞ |
1 |
|
|
|
|
|
|
∞ |
1 |
|
|
|
|
|
|
∞ |
|
|
|
n+1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
π 2 = |
4π |
2 |
+4∑ |
cos nπ |
= 4π 2 +4∑ |
(−1)n |
|
|
∑ |
(−1)2 |
=π 2 . |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
3 |
|
|
|
n=1 |
n |
|
|
|
|
|
|
3 |
|
n=1 |
n |
|
|
|
|
|
|
|
n=1 |
|
|
|
n |
12 |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
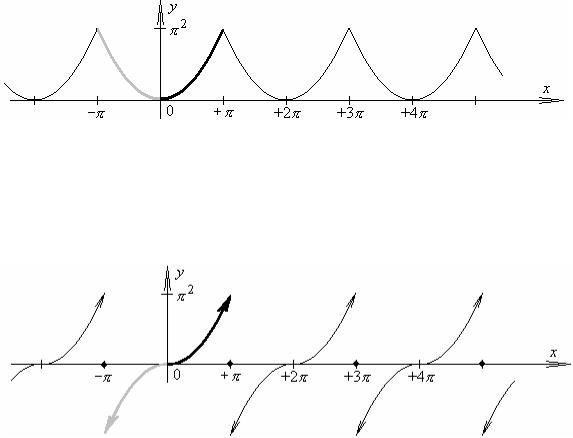
№ 46.2.
π |
|
|
|
|
|
|
|
l |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
π |
|
|
|
l |
|
|
l |
|
2 |
|
l |
2 |
2 |
|
||||||
Положим l |
x = y x = |
|
|
|
y |
|
|
|
|
|
|
g( y) = g (l x)= f (x) = f ( |
|
y)=( |
|
y) |
|
=( |
|
) |
y |
|
. |
||||||||||||||||||||||||||
|
π |
|
|
|
|
|
π |
π |
|
π |
|
||||||||||||||||||||||||||||||||||||||
a) f (x) = x2 , |
−l ≤ x ≤+l |
|
|
|
g( y) =( |
l |
)2 y2 , |
−π ≤ y ≤+π |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
π |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
Используя найденное в № 46.1. a) |
|
разложение |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
g( y) =( |
l |
) |
2 |
y2 =( |
l |
|
) |
2 |
|
|
|
2 |
|
|
|
∞ |
n |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
π |
|
|
|
|
+4∑ |
(−1) |
cos ny |
, |
|
−π ≤ y ≤+π |
|
|
|
||||||||||||||||||||||||||||||
|
|
|
π |
|
|
|
|
|
|
2 |
|
|
|
|
|||||||||||||||||||||||||||||||||||
получаем: |
|
|
|
π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
n=1 |
n |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
f (x) =x2 =l32 +4( |
|
) |
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
l |
2 |
|
|
∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
∑(−n1)2 |
cos n πl x, |
|
|
|
−l ≤ x ≤+l |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
π |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
b) f (x) = x2 , |
0 ≤ x ≤2l |
|
|
g( y) =( |
l |
)2 y2 , |
0 ≤ y ≤2π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
π |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
Используя найденное в № 46.1. b) |
|
разложение |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
g( y) =( |
l |
) |
2 |
|
=( |
l |
) |
2 |
|
4π |
|
2 |
|
|
|
|
|
|
|
∞ |
|
∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
y2 |
|
|
|
|
|
|
+4∑ |
1 |
cos ny −4π∑ |
1n sin ny , |
|
|
0 < y <2π |
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
2 |
|
|
|
|||||||||||||||||||||||||||||||||||||||
получаем: |
π |
|
|
|
|
π |
|
|
|
|
|
3 |
|
|
|
|
|
|
n=1 n |
|
n=1 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
+4( |
|
|
|
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
(x) = x2 = 4l |
2 |
|
l |
|
2 |
|
|
|
∞ |
|
|
1 |
|
|
|
|
|
|
∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
f |
|
|
|
|
|
|
∑ |
|
|
cos n π |
x −π ∑1n sin n π |
x , |
|
0 < x <2l |
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
2 |
|
|
|
|||||||||||||||||||||||||||||||||||||||
№ 46.3. |
|
|
|
3 |
|
|
|
|
|
π |
|
|
|
n=1 n |
|
|
|
|
l |
|
n=1 |
|
|
l |
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a) f (x) = x2 |
0 ≤ x ≤π . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
a.1) Разложение функции в ряд по |
|
|
|
Cos – это ряд Фурье четного продолжения функции, |
|||||||||||||||||||||||||||||||||||||||||||||
с интервала 0 ≤ x ≤ +π на интервал −π ≤ x ≤ 0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
В данном случае, четное продолжение совпадает с естественным заданием функции, так что разложение в ряд по Cos - это разложение, полученное в № 46.1. a) .
x2 =π 2 |
∞ |
n |
|
+4∑ |
(−1)2 cos nx, |
0 ≤ x ≤+π |
|
3 |
n=1 |
n |
|
a.2) Разложение функции в ряд по Sin - это ряд Фурье нечетного продолжения функции с интервала 0 ≤ x ≤ +π на интервал −π ≤ x ≤ 0 .
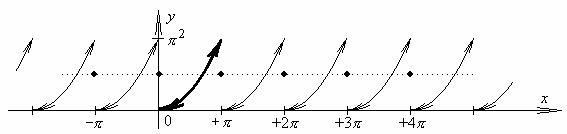
Имеем: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
an |
= 0, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
b |
= 2 |
π |
f (x)sin nxdx = 2 |
π |
x2 sin nxdx =− 2 |
|
π |
x2 d cos nx =− |
2 |
|
x2 |
cos nx |
|
π |
− |
π |
cos nxdx2 |
|
= |
||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
n |
|
|
∫ |
|
|
|
|
|
|
∫ |
|
|
|
|
|
πn ∫ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∫ |
|
|
|
||||
|
π |
|
|
|
π |
|
|
|
|
|
|
|
|
|
|
|
πn |
|
|
|
|
|
0 |
|
|
|
|
|
|
||||||||||
|
|
|
0 |
|
|
|
|
|
|
0 |
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|||
|
|
|
2 |
|
|
|
|
π |
|
|
|
|
|
2 |
|
|
(−1)n − 2 |
π |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
=− |
|
π 2 |
cos nπ −2 |
∫ |
x cos nxdx =− |
π 2 |
∫ |
xd sin nx = |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
πn |
|
|
|
|
|
|
|
|
|
|
πn |
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
2 |
|
π 2 |
(−1)n − 2 |
|
|
|
π |
|
π |
|
|
|
|
|
|
=− 2 |
π 2 (−1)n |
|
2 |
cos nx |
|
π |
) |
|
|
|
||||||||||
|
=− |
|
|
x sin nx |
|
− |
|
sin nxdx |
|
− |
|
= |
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
πn |
|
|
n |
|
|
|
0 |
|
∫ |
|
|
|
|
|
|
πn ( |
|
|
|
|
|
|
n2 |
|
|
|
|
|
0 |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
=−π2n (π 2 (−1)n − |
2 |
( |
(−1)n −1))=− 2nπ (−1)n + |
4 |
((−1)n −1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
2 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
πn |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∞ |
|
|
|
|
|
4 |
((−1)n −1))sin nx, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
x2 =∑(− 2nπ (−1)n + |
|
|
0 ≤ x <+π |
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
n=1 |
|
|
|
|
|
πn |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
a.3) Для разложения функции, заданной на интервале 0 ≤ x ≤ +π , в ряд Фурье “растянем” |
||||||||||||
интервал в 2 раза: |
|
|
|
|
|
|
|
y |
|
|
|
|
0≤x ≤π 0≤2x ≤2π 2x = y x = |
|
|
|
|
||||||||
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
(12 y)=(12 y)2 = 14 y2 . |
|
|
|
|
|
|||||||
g( y) = g (2x)= f (x) = f |
|
|
|
|
|
|||||||
Используя найденное в № 46.1. b) разложение |
|
|
|
|||||||||
|
|
|
|
∞ |
|
|
∞ |
|
|
|||
1 y2 = 1 |
4π 2 |
+4∑ |
1 |
cos ny |
−4π∑1 sin ny , |
0 < y <2π |
||||||
|
||||||||||||
4 |
4 |
3 |
|
n=1 n2 |
|
|
n=1 n |
|
|
|||
получим: |
|
|
∞ |
|
|
|
|
∞ |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|||
x2 = |
π 2 +∑ |
cos 2nx −π∑ |
1 sin 2nx, |
|
0 < x <+π. |
|||||||
|
|
|||||||||||
|
|
3 |
n=1 |
n2 |
n=1 |
n |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|||

47. Интегралы Фурье. Cos– и Sin- преобразования Фурье
Условия.
Представить функцию интегралом Фурье. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
№ 47.1. |
1, |
|
|
|
x |
<α |
|
|
|
|
|
|
|
|
|
|
|
|
№ 47.1. |
|
α − |
x |
, |
|
|
|
|
|
|
|
x |
|
<α |
|||||||||||||||
f (x) = |
|
|
|
x |
|
|
>α |
|
|
|
|
|
|
|
|
|
|
|
|
f (x) = |
|
|
|
|
|
|
|
|
|
|
|
x |
|
>α |
||||||||||||||
|
0, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0, |
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
№ 47.2. |
sign x, |
|
|
|
x |
|
|
<α |
|
|
№ 47.2. |
|
αsign x − x, |
|
|
|
x |
|
<α |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
f (x) = |
0, |
|
|
|
|
|
x |
|
|
>α |
|
|
f (x) = |
|
0, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
>α |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
sin x, |
|
x |
|
|
≤π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
π |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
№ 47.3. |
f (x) = |
0, |
|
|
|
|
x |
|
|
>π |
|
|
|
№ 47.3. |
|
cos x, |
|
x |
|
|
|
≤ |
2 |
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
f (x) = |
|
0, |
|
x |
|
|
>π |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
0, |
|
|
|
|
|
− ∞ < x < 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
f (x) = ex , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
№ 47.4. |
f (x) = |
−x |
, |
|
|
0 |
< |
x |
< +∞ |
|
|
№ 47.4. |
− ∞ < x < 0 |
|||||||||||||||||||||||||||||||||||
|
e |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 < x < +∞ |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0, |
|
||||||||||||||||||||||
Найти Cos - ( Sin -) преобразованиеФурьефункцииивосстановитьпонемуданнуюфункцию. |
||||||||||||||||||||||||||||||||||||||||||||||||
№ 47.5. |
f (x) = e−x , |
|
|
|
|
|
0 < x < +∞ |
|
|
№ 47.5. |
f (x) = e−x , |
0 < x < +∞ |
||||||||||||||||||||||||||||||||||||
Найти преобразование Фурье функции и |
восстановить по нему данную функцию. |
|||||||||||||||||||||||||||||||||||||||||||||||
№ 47.6. |
|
0, |
|
|
|
|
|
− ∞ < x < 0 |
|
|
№ 47.6 |
|
|
x |
, |
|
− ∞ < x < 0 |
|||||||||||||||||||||||||||||||
f (x) = |
−x |
, |
|
|
|
0 < x < +∞ |
|
|
f (x) = e |
|
|
|||||||||||||||||||||||||||||||||||||
|
e |
|
|
|
|
|
|
|
|
0, |
0 |
< x < +∞ |
||||||||||||||||||||||||||||||||||||
Теория. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Если функция y = f (x) кусочно-непрерывно дифференцируемая |
на |
|
|
любом конечном |
||||||||||||||||||||||||||||||||||||||||||||
интервале, |
причем ее точки разрыва x0 |
регулярны |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f (x0 ) = |
f (x0 +0) + f (x0 |
−0) |
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
и абсолютно интегрируема на всей оси, то ее можно представить интегралом Фурье:
|
f (x) =∞∫(a( y) cos xy +b( y)sin xy)dy, |
−∞< x <+∞ |
|||||
|
|
0 |
|
|
|
|
|
1 |
+∞ |
|
1 |
+∞ |
|
|
|
a( y) =π |
∫ f (x) cos yxdx, |
b( y) =π |
∫ f (x)sin yxdx. |
|
|||
|
−∞ |
|
|
|
−∞ |
|
|
Если дополнительно функция f (x) четная или нечетная, |
то ее интеграл Фурье имеет |
||||||
соответственно только четную или нечетную составляющую: |
|
||||||
четная |
|
|
|
|
|
|
нечетная |
f (x) =∞∫a( y) cos xydy, |
−∞< x <+∞ |
|
f (x) =∞∫b( y)sin xydy, |
−∞< x <+∞ |
|||
0 |
|
|
|
|
0 |
|
|
a( y) =π2 ∞∫ f (x) cos yxdx, |
b( y) =0. |
|
b( y) =π2 ∞∫ f (x)sin yxdx, |
a( y) =0. |
|||
0 |
|
|
|
|
0 |
|
|
Отсюда вытекает возможность представить функцию, заданную только на полуоси [0, +∞) , как Cos – или Sin - преобразование Фурье соответственно своего Cos - или Sin -
преобразования Фурье: |
|
|
|
|
|
Cos -преобразование Фурье |
|
|
Sin -преобразование Фурье |
||
Fc ( y) = |
π2 ∞∫ f (x) cos yxdx |
0 ≤ x, y <+∞ |
Fs ( y) = |
π2 ∞∫ f (x) sin yxdx |
0 ≤ x, y <+∞ |
|
0 |
|
0 |
||
f (x) = |
π2 ∞∫Fc ( y) cos xydy |
|
f (x) = |
π2 ∞∫Fs ( y) sin xydy |
|
|
0 |
|
|
0 |
|

Интегральной формуле Фурье можно придать “симметричный” вид, переходя к комплексной форме:
|
1 |
+∞ |
|
1 |
|
+∞ |
|
F( y) = |
∫ f (x)e−iyxdx f (x) = |
|
∫ F( y)e+ixy dy |
||||
2π |
2π |
||||||
|
−∞ |
|
−∞ |
||||
Функция F( y) называется преобразованием |
Фурье |
функции f (x) , которая |
|||||
восстанавливается по своему преобразованию Фурье как обратное преобразование Фурье.
Решения.
№ 47.1.
Доопределим |
функцию |
1, |
|
x |
|
<α |
в точках разрыва |
|
значением |
|||||
|
|
|
||||||||||||
f (x) = |
|
x |
|
>α |
±α |
|||||||||
f (±α) =1+0 |
= 1 |
: |
0, |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Учитывая, что данная функция четная, получим b( y) = 0.
Далее: |
|
|
|
|
|
|
|
α |
|
|
|
|
|
|
2 |
∞ |
|
2 |
α |
2 sin yx |
|
|
|
2 sinα y |
|||
|
|
|
|
||||||||||
a( y) = |
|
∫ |
f (x) cos yxdx = |
|
∫1 cos yxdx = |
|
y |
|
|
= |
|
|
y |
π |
π |
π |
|
0 |
π |
||||||||
|
|
0 |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
∞
= 2 ∫sin yα
f (x) π y cos xydy .
0
Замечание. Полагая чтоx = 0 , получим интеграл Дирихле:
|
|
|
|
∞ sinα y |
|
|
|
|
|
π |
|
|
|
|
|
|
|
|
∫ |
|
dy = 2 sign |
α |
. |
||||||
|
|
|
y |
|||||||||||
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
№ 47.2. |
|
|
sign x, |
|
x |
|
|
<α |
|
|
|
|||
Доопределим |
функцию |
|
|
|
в |
точках разрыва ±α значением |
||||||||
|
|
|
||||||||||||
f (x) = |
0, |
|
x |
|
|
>α |
||||||||
f (±α) = ±1+0 |
=± 1 |
. : |
|
|
|
|
|
|
||||||
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
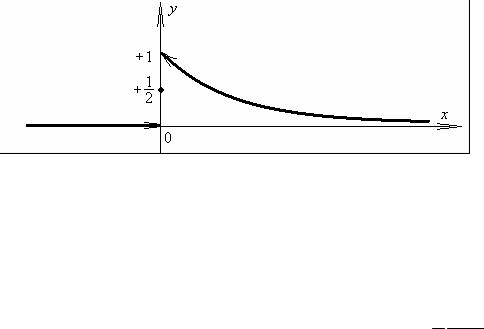

Замечание. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
−x |
|
|
1 |
|
∞ |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
∞ |
1 |
|
|
|
|
|
|
|
|
|
|
π |
|
|
−x |
|
|
|
||||||||||
x >0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
e |
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cos xy + |
|
|
|
|
sin xy |
dy |
|
|
|
|
|
|
|
|
|
|
|
cos xydy = |
|
|
e |
|
|
|
|
|
||||||||||||||||
|
|
|
|
π |
|
|
|
|
|
|
|
|
2 |
|
1+ y |
2 |
|
|
|
∫1+ y |
2 |
|
|
2 |
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
∫ 1+ y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
∞ |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 < x <+∞ |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
∞ |
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
−x <0 |
|
0 = |
1 |
|
|
|
|
|
1 |
|
|
|
|
|
cos (−x) y + |
|
|
|
|
|
sin (−x) y |
dy |
|
|
|
|
|
|
|
sin xy dy =π e−x |
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
2 |
|
∫1+ y |
2 |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
1+ y |
|
|
|
|
|
|
|
1+ y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
π ∫ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
№ 47.5. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f (x) = e−x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Найдем Cos - преобразование Фурье функции |
|
(0 < x < +∞) : |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
π2 |
+∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
π2 |
+∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+∞ |
|
|
|
|
|
|
|
|
|
|
|
π2 |
|
|
+∞ |
|
|
|
|
|
|
|||||||
Fc ( y) = |
∫ |
|
f (x) cos yxdx = |
∫ e−x cos yxdx = π2 |
Re ∫ e−xe−iyx dx = |
Re |
∫ |
e−(1+iy)xdx = |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
||
= |
2 |
Re |
e−(1+iy)x |
|
|
+∞ = |
2 |
Re |
e−(1+iy)∞ −e−(1+iy)0 |
= 2 |
Re |
|
|
1 |
|
|
|
= |
2 |
Re |
|
1−iy |
= |
2 |
1 |
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
π |
|
|
|
−(1+iy) |
|
0 |
|
|
|
π |
|
|
|
|
|
−(1+iy) |
|
|
π |
|
|
1 |
+iy |
|
π |
|
1+ y2 |
|
π 1+ y2 |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f (x)= π2 |
+∞∫Fc ( y)cos xydy |
e−x = π2 |
+∞∫ π2 |
1 |
|
cos xydy=π2 |
+∞∫ |
1 |
cos xydy, |
0<x<+∞ |
||||||||||||||||||||||||||||||||||||||||||||||||||||
1+ y2 |
1+ y2 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Замечание. |
|
|
|
|
|
При |
|
|
|
|
|
нахождении |
|
|
|
Cos - преобразования |
|
|
|
Фурье |
|
|
|
функции |
||||||||||||||||||||||||||||||||||||||
f (x) = e−x |
|
(0 < x < +∞) |
можно |
было воспользоваться |
соотношением, |
полученным в |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
предыдущем примере № 47.4. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
∞ |
1 |
|
|
|
|
|
|
|
|
|
|
π |
|
|
|
|
|
|
|
|
2 |
∞ |
|
|
|
|
|
|
|
|
|
|
|
π |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−x |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
−x |
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
∫ |
|
|
cos xydy = |
2 e |
|
|
|
|
|
|
|
|
∫ |
|
cos xydy = |
2 e |
|
, |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
1+ y2 |
|
|
|
|
|
π |
1+ y2 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
которое задает Cos - преобразование некоторой функции. Учитывая, что функция восстанавливается по своему Cos - преобразованию в свою очередь, как его Cos - преобразование, получим:
|
1 |
= |
2 |
|
∞ π e−x cos yxdx =∞ e−x cos yxdx |
F ( y) = |
2 |
∞ e−x cos yxdx = |
2 |
|
1 |
. |
|||||||
|
|
|
|
|
|||||||||||||||
1+ y2 |
π ∫ 2 |
|
∫ |
|
|
c |
π |
∫ |
|
π 1+ y2 |
|||||||||
|
|
|
|
0 |
|
|
0 |
|
|
|
|
0 |
|
|
|
|
|
|
|
№ 47.6. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Преобразование Фурье функции f (x) |
определяется как интеграл |
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
1 |
|
+∞ |
f (x)e−iyxdx = |
1 |
+∞ |
(cos yx −i sin yx)dx = |
π |
(a( y) −ib( y)). |
||||||
|
F( y) = |
|
|
∫ |
∫ f (x) |
||||||||||||||
|
|
|
|
||||||||||||||||
|
|
|
|
|
2π |
−∞ |
|
2π |
−∞ |
|
|
|
2 |
|
|
|
|
|
|
Воспользуемся решением примера № 47.4., в котором функции-коэффициенты a( y), b( y)
были найдены “одновременно”. Теперь видно, что по существу было найдено преобразование Фурье:
F( y) = |
π |
(a( y) −ib( y))= |
π 1 |
1−iy |
= |
1 |
|
1−iy |
. |
|
|
|
|||||||
|
2 |
|
2 π 1+ y2 |
|
2π 1+ y2 |
||||
Учитывая, что функция восстанавливается по своему преобразованию Фурье в свою очередь как его обратное преобразование Фурье, получим:
|
1 |
+∞ |
1 |
|
1−iy |
|
+ixy |
|
1 |
+∞ 1−iy |
|
+ixy |
|
0, |
|
−∞<x <0 |
|||
f (x) = |
|
|
|
|
|
|
e |
|
dy = |
|
|
|
|
e |
|
dy = |
−x |
|
|
2π |
∫ |
2π |
1+ y |
2 |
|
2π ∫ |
1+ y |
2 |
|
, |
0 <x <+∞ |
||||||||
|
|
|
|
|
|
|
|
e |
|
||||||||||
|
|
−∞ |
|
|
|
|
|
|
|
|
−∞ |
|
|
|
|
|
|
|
|
