Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Харьковский Национальный Университет им. В. Н. Каразина

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

матан

.pdf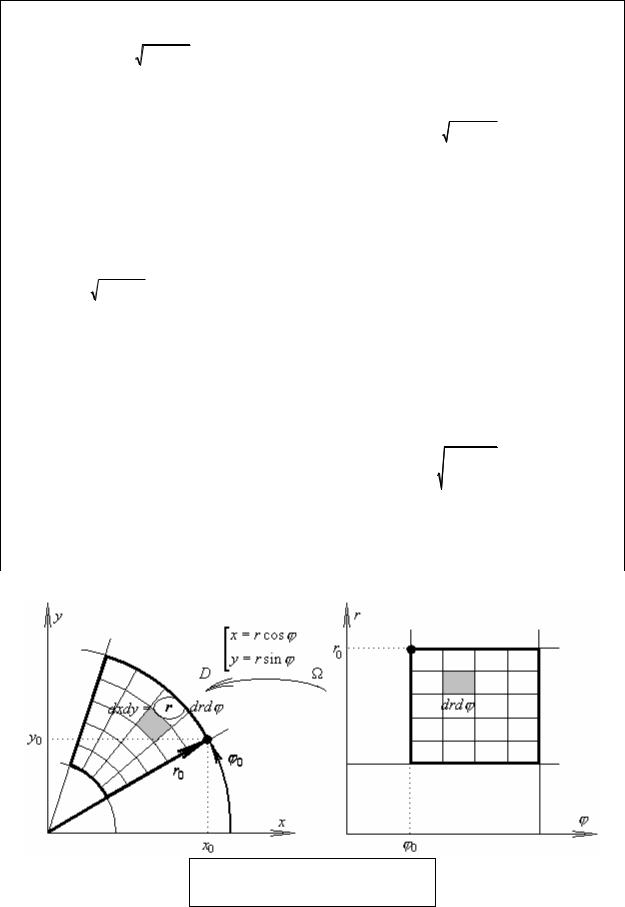

Скачиваний:

Добавлен:

23.02.2015

Размер:

1.44 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 45 / 145 6 7 8 9 10 11 12 13 14 > Следующая >>>

33. Двойные интегралы. Переход к полярным координатам

Условия.

№ 33.1. Найти массу пластины, ограниченной заданными кривыми, с поверхностной плотностью ρ = ρ(x, y) .

x2 + y2 =a2 , ρ = x2 + y2 .

№ 33.2. Найти заряд пластины, ограниченной заданными кривыми, с поверхностной плотностью ρ = ρ(x, y) .

x2 + y2 =2ax, ρ = x2 + y2 .

x2 + y2 =ax, ρ = x2 + y2 .

№ 33.3. Найти центр тяжести однородной пластины, ограниченной заданными кривыми.

x2 + y2 =2ay.

x2 + y2 =ax.

Найти объем тела, ограниченного поверхностями.

№ 33.4.

z =e−( x2 +y2 ) ,

z =0, x2 + y2 =a2 .

№ 33.4.

z = x2 + y2 ,

z =0, x

+ y

№ 33.5.

z = x2 + y2 ,

z =0,

x2 + y2 =ax.

№ 33.5.

z = x2 + y2 ,

z =0,

x2 + y2 =ay.

Найти площадь пластины, ограниченной кривыми.

№ 33.6. (x2 + y2 )2 = x2 − y2 .

№ 33.6. (x2 + y2 )2 =2xy.

№ 33.7.

r = a(1 + cosϕ).

№ 33.7.

r = asin 3ϕ

№ 33.8. Найти массу пластины, ограниченной заданными кривыми, с поверхностной плотностью ρ = ρ(x, y) .

=1,

ρ =

=1, ρ =

№ 33.9. Найти площадь пластины, ограниченной кривыми.

xy =a, xy =b,

(0 <a <b)

xy =a, xy =b,

(0 <a <b)

y =cx2 , y =dx2 , (0 <c <d).

y =cx, y =dx,

(0 <c <d).

Теория.

∫∫f (x2 + y2 )dxdy =∫∫f (r2 ) r drdϕ

D Ω

Решения.

№ 33.1.

m =∫∫ρ(x, y)dxdy =∫∫			x2 + y2 dxdy =→
D		D
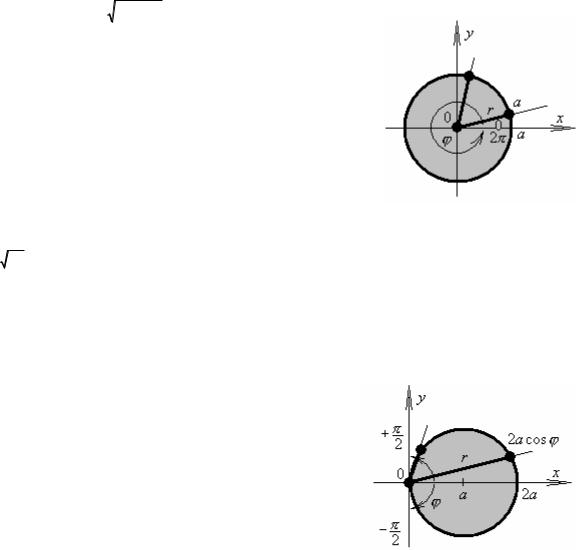
Кривая x2 + y2 = a2		– это окружность радиуса a с центром
в начале координат (0,0) . Учитывая вид подынтегральной
функции	f (x2 + y2 )		и “круговую” форму области		D ,
перейдем к полярным координатам.
Поскольку	x2 + y2 =a2 →r =a ,
	x2 + y2 =a2 →r =a ,
то
D ={x2 + y2 ≤a2 } → Ω={r ≤a}={0 ≤ϕ ≤2π, 0 ≤r ≤a}.
Тогда		2∫π (	∫a r2 dr	)dϕ =2π ∫a r2 dr =2π 13 r3
→=∫∫ r2	r drdϕ =				0a = 32 πa3 .
	r drdϕ =

Ω		0	0	0

№ 33.2.

q =∫∫ρ(x, y)dxdy =∫∫(x2 + y2 )dxdy =→

Кривая

x2 + y2 =2ax (x2 −2ax +a2 )+ y2 =a2 (x −a)2 + y2 =a2

это “смещенная” окружность радиуса a с центром в

точке (a,0) . Учитывая вид подынтегральной функции

f (x2 + y2 ) и “круговую” форму области D , перейдем к

полярным координатам.

Поскольку

x2 + y2 =2ax → r2 =2ar cosϕ r =2a cosϕ,

то

π ≤ϕ ≤+

D ={x2 + y2 ≤2ax}

→ Ω={r ≤2a cosϕ}={−

, 0 ≤r ≤2a cosϕ}.

Тогда

+π

2a cos

2a cosϕ

16a4

→=∫∫r

r drdϕ =

∫

dϕ = ∫

dϕ =

∫cos

ϕdϕ =

Ω

−

− 2

+π

1+cos 2ϕ 2

=4a

∫

(cos2 ϕ) dϕ

=4a

∫

dϕ

∫

+2cos 2ϕ +cos2 2ϕ)dϕ =

−π

+π

1+cos 4ϕ

∫

(1+2cos 2ϕ+

)dϕ

∫1dϕ+0

+0=

π.

∫(2

+2cos 2ϕ+2 cos 4ϕ)dϕ

=2 a

−π

№ 33.3.

Из физических понятий очевидно, что центр масс однородного круга находится в его центре: (x0 , y0 ) = (0, a). Цель приведенных ниже расчетов, в частности, показать адекватность математических формул интуитивным представлениям.

Найдем массу пластины:

m =∫∫ρ(x, y)dxdy =ρ∫∫1 dxdy =→

Кривая

x2 + y2 =2ay x2 +(y2 −2ay +a2 )=a2 x2 +(y −a)2 =a2

это “смещенная” окружность радиуса a с центром в точке

(0, a) . Учитывая вид подынтегральной функции

f (x2 + y2 )

и “круговую” форму области

D ,

перейдем к полярным

координатам.

Поскольку

x2 + y2 =2ay → r2 =2ar sin ϕ r =2a sin ϕ,

то

D ={x2 + y2 ≤2ay} → Ω={r ≤2a sin ϕ}={0 ≤ϕ ≤π,

0 ≤r ≤2a sin ϕ}.

Тогда

2a∫sinϕ r dr

→=ρ∫∫r drdϕ =ρ∫π (

)dϕ =ρ 12 ∫π r2

02a sinϕ dϕ =

Ω

∫π (2a sinϕ)2 dϕ =

4a2 ∫π 1−cos2

2ϕ dϕ = ρa2 ∫π (1−cos 2ϕ)dϕ = ρπa2 .

Найдем координаты центра масс:

2a sinϕ

(

cosϕdr )

ρ 1

2a sinϕ

x0 =

∫∫xρdxdy=

∫∫r cosϕ r drdϕ=

∫

dϕ=

∫cosϕ r

dϕ=

Ω

8a3ρ sin4 ϕ

∫

(2asinϕ) cosϕdϕ=

8a3 ∫sin3 ϕd sinϕ=

=0.

y0 =

∫∫yρdxdy =

∫∫r sinϕ r drdϕ =

∫π (

2a∫sinϕ r2 sinϕdr

)dϕ =

13 ∫π sinϕ r3

02a sinϕ dϕ =

Ω

ρ π

8ρa3 π 1−cos 2ϕ 2

∫

(2a sinϕ) sinϕdϕ =

8a3

∫

(sin2

ϕ)

dϕ =

3m ∫

dϕ =

2ρa3

(1−2cos 2ϕ

+cos2 2ϕ)dϕ =

2ρa3 π

−

2cos 2ϕ

1+cos 4ϕ

∫

dϕ =

= 23ρma3 ∫π (32 −2cos 2ϕ + 12 cos 4ϕ)dϕ = 23ρma3 (32 π −0 +0)= m1 ρπa3 =a.

№ 33.4.

V =∫∫( fB (x, y) − fH (x, y))dxdy =→

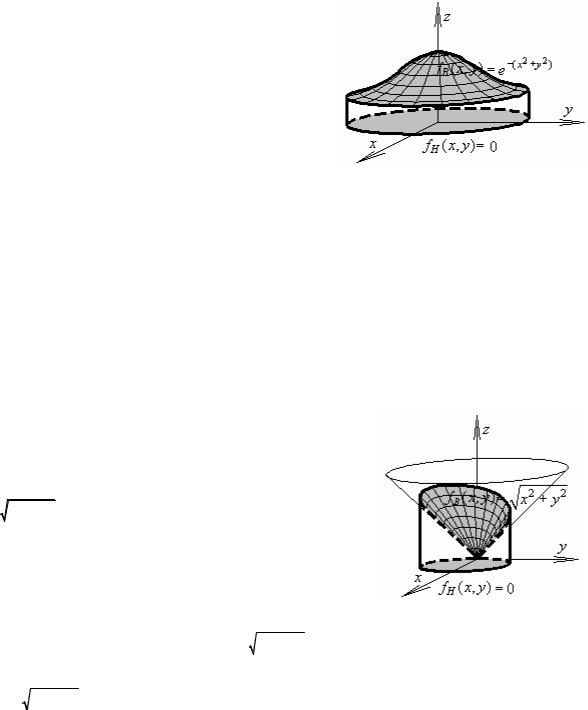
Выделим среди поверхностей { z =e−( x2 +y2 ) , z =0, x2 + y2 =a2 }, ограничивающих объем V ,

те, уравнения которые не содержат переменной z . На плоскости xOy эти уравнения задают

некоторые кривые, а в пространстве – цилиндрические поверхности, параллельные оси Oz , в основании которых лежат эти кривые. В

данном

примере

окружность

{ x2 + y2 =a2 }

ограничивает круг

D ={ x2 + y2 ≤a2 }

радиуса

центром в начале координат, так что поверхности

{z =0

≤

z =e−( x2 +y2 ) ,

(x, y) D}, играющие роль

“нижней” и “верхней”, достаточно построить схематично.

→=∫∫(e−(x2 +y2 ) −0)dxdy =→

Учитывая вид подынтегральной функции f (x2 + y2 )

и “круговую” форму области D ,

перейдем к полярным координатам.

D ={x2 + y2 ≤a2 } → Ω={r ≤a}={0 ≤ϕ ≤2π, 0 ≤r ≤a}.

Имеем

2π

1 a

−r2

−r2 2

−r2

(

−a2 )

∫∫

∫

→=

r drdϕ =

rdr

2 ∫

=−πe

dϕ =2π

0 =π 1−e

Ω

№ 33.5.

V =∫∫( fB (x, y) − fH (x, y))dxdy =→

Выделим среди поверхностей

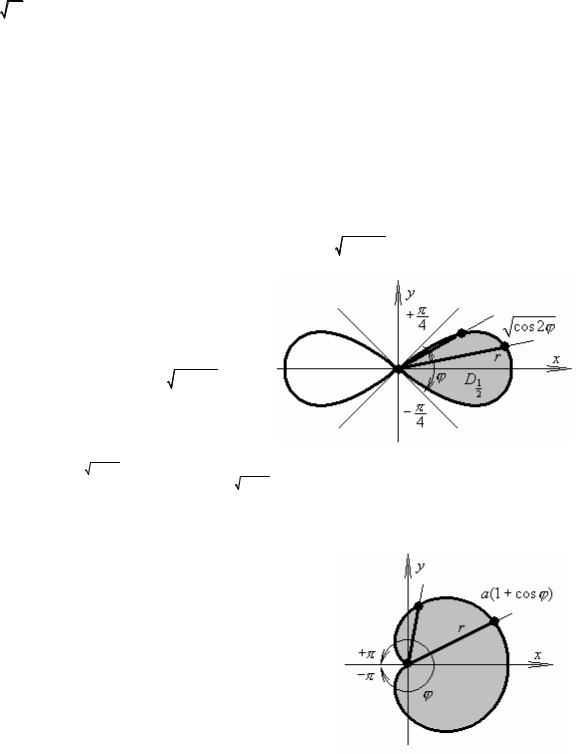
{ z = x2 + y2 , z =0, x2 + y2 =ax} ,

ограничивающих объем V , те, уравнения которых не

содержат переменной z . В данном примере “смещенная”

окружность

{ x2 + y2 =ax}

ограничивает

круг

D ={ (x −

2 )

+ y

≤

(2 )

} радиуса

с центром в точке

(a2 ,0), так что поверхности {z =0 ≤ z = x2 + y2 ,

(x, y) D}, играющие роль “нижней” и

“верхней”, достаточно построить схематично.

→=∫∫( x2 + y2 −0)dxdy =→

Учитывая вид подынтегральной функции f (x2 + y2 ) и “круговую” форму области D , перейдем к полярным координатам.

D ={x2 + y2 ≤ax}→Ω={r ≤a cosϕ}={−π2 ≤ϕ ≤+π2 ,0≤r ≤a cosϕ}.

Имеем:

+π2

a cosϕ

+π2

→=∫∫

r drdϕ= ∫(

∫ r

)dϕ=3

∫r

dϕ= 3 ∫cos

ϕdϕ= 3

∫cos

ϕ cosϕdϕ=

a cosϕ

Ω

−π

+π

=a33 ∫2 (1−sin2 ϕ)d sinϕ=a33 +∫1(1−t2 )dt =23a3 +∫1(1−t2 )dt =32 a3 (t −13 t3 )

=32 a3 (1−13)=94 a3

−

−1

№ 33.6.

(x2 + y2 )2 = x2 − y2

Кривая

L ={

}, ограничивающая область

D ,

в полярной

системе

координат имеет более простое описание:

−π

+π k ≤ϕ ≤+π

(r2 )2 =r2 cos2 ϕ −r2 sin2 ϕ

r2 =cos 2ϕ

r = cos 2ϕ,

+π k

S =∫∫1 dxdy =2∫∫1 dxdy =→

D1 →Ω={−π

≤ϕ ≤+π ,

0 ≤r ≤ cos 2ϕ}

+π4

cos 2ϕ

+π4

=1.

→=2∫∫rdrdϕ=2 ∫

∫

rdr dϕ=2 2

∫r

dϕ= ∫cos 2ϕdϕ=2 ∫cos 2ϕdϕ=sin 2ϕ 0

Ω

−π

cos 2ϕ

−π

+π4

№ 33.7.

S =∫∫1 dxdy =→

Перейдем к полярным координатам:

D → Ω ={−π ≤ϕ ≤ +π,

0 ≤ r ≤ a(1 + cosϕ)}

∫∫

+π

a(1+cosϕ)

∫

→=

r drdϕ =

r dr

dϕ =

Ω

−π

+π

a(1+cosϕ)

2 +π

= 12 ∫r2

dϕ = a2

∫(1+cosϕ)2 dϕ =

−π

= a

+π

(1+2cos

ϕ +cos2 ϕ)dϕ

= a

+π

2cosϕ +

1+cos 2ϕ

∫

dϕ =

∫

−π

+π

∫

2 dϕ +0

+0 =

2π =

π.

−π

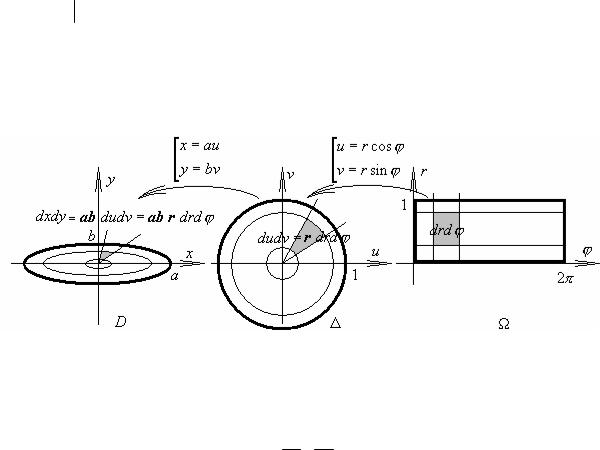
Сравнить: нахождение площади “криволинейного сектора” с помощью двойного интеграла с нахождением с помощью однократного интеграла:

S =∫∫1 dxdy =[D →Ω={α ≤ϕ ≤β,	rH (ϕ) ≤r ≤rB (ϕ)]=∫∫r drdϕ =∫β (		rB∫(ϕ) r dr )dϕ =
D	Ω	α	rH (ϕ)

ββ

= 12 ∫r2	rB (ϕ)	dϕ = 12 ∫(rB2 (ϕ) −rH2 (ϕ))dϕ .
	rH (ϕ)

αα

№33.8.

					2		y	2
m =	∫∫	ρ(x, y)dxdy =		x		+	y		dxdy =→
	∫∫		∫∫ a2				b2
	D		D

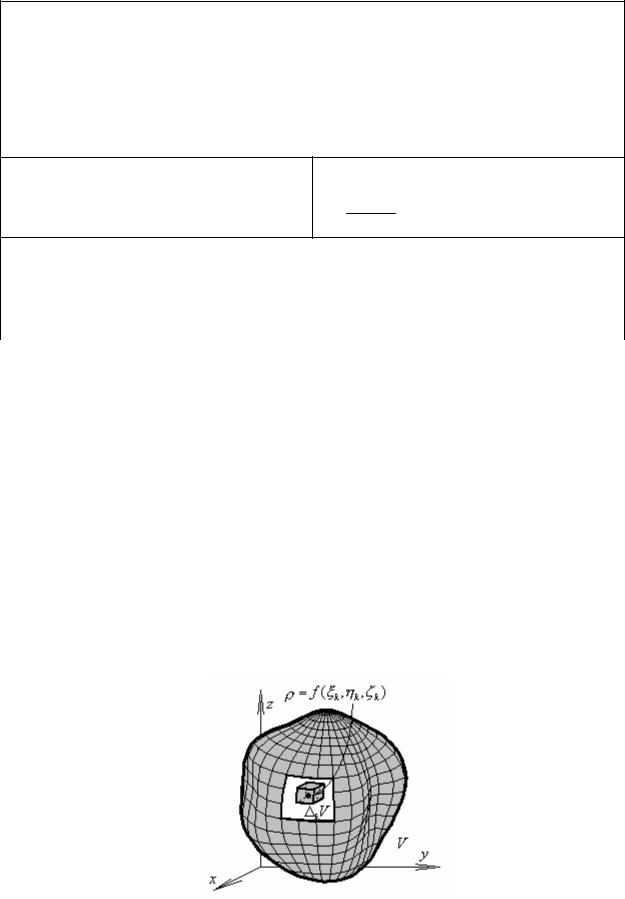
Перейдем от старых координат (x, y) к промежуточным (u,v) , полагая что:

x =au

dxdy =

D(x, y)

dudv =

xu′ xv′

dudv =

dudv =ab dudv

y =bv

D(u, v)

yu′ yv′

D ={x2 + y2 ≤1}→∆={u2 +v2 ≤1}. a2 b2

→=∫∫(u2 +v2 ) ab dudv =→

∆

Переходя далее от промежуточных координат (u,v) к полярным (r,ϕ)

u =r cosϕ

v =r sinϕ

находим:

→=ab∫∫r2

Ω

dudv =

D(u, v)

drdϕ =

ur′

uϕ′

drdϕ =

cosϕ −r sinϕ

=r drdϕ

vr′

vϕ′

sinϕ

r cosϕ

D(r,ϕ)

∆={u2 +v2 ≤1}→Ω={r ≤1}={0≤ϕ ≤2π,

0≤r ≤1},

2π

r drdϕ =ab ∫(

∫r

dr )dϕ =2πab∫r

dr =2πab

4 r

0 =

2 πab.

Замечание. Координаты (r,ϕ) для исходных декартовых координат (x, y) получили название обобщенных полярных координат

x =ar cosϕ	D(x, y)	=ab r
x =ar cosϕ

y =br sinϕ	D(r,ϕ)
y =br sinϕ	D(r,ϕ)

№ 33.9.

Область D , очевидно, можно описать в виде:

D ={a ≤xy ≤b, c ≤

≤d}.

Перейдем от старых координат (x, y) к новым (u,v) , полагая что:

u = xy

−1

1 u−32 v−13

−1 u13 v−34

x =u

3 v

dxdy = D(x, y) dudv =

dudv =

dudv

2 1

D(u, v)

1 1

v =

− 3

−

y =u

D →Ω={a ≤u ≤b,

c ≤v ≤d}.

Тогда:

dudv =∫b (

∫d

dv )du =

S =∫∫1 dxdy =∫∫

DD((ux,, vy))

dudv =∫∫

Ω

=13 ∫b du∫d 1v dv = 13 (b −a)ln v

cd =13 (b −a)ln dc .

34. Тройные интегралы. Физические и геометрические приложения

Условия.

№ 34.1. Найти массу тела, ограниченного заданными поверхностями, с объемной плотностью ρ = ρ(x, y, z) .

z =x2 y, z =0, y =(x −1)2 , y = x +1;			z = xy2 , z =0, y =4x − x2 , y =4 − x;
ρ =	z	.	ρ =	z	.
	x3 y2			x2 y3

№ 34.2. Найти заряд тела, ограниченного заданными поверхностями, с объемной плотностью ρ = ρ(x, y, z) .

z =π, z = x		4	y	2	, y =	1	(	)
z =π, z = x			y		, y =	2		x +1 , y =1, x =−1;
ρ =	cos z		.
ρ =	sin x4 y2		.
	sin x4 y2

z =π	, z = x3 y, y =1− x, y =1, x =1;
2

ρ = sin z . cos x3 y

№ 34.3. Найти центр масс однородной пирамиды, ограниченной плоскостями.

6x + 3y + 2z = 6, z = 0, y = 0, x = 0.

2x + y + 2z = 2, z =1, y = 0, x = 0.

№ 34.4. Найти объем тела, ограниченного поверхностями.

z = xy, z = 0, x + y =1.

z = xy, z = 0, y = x, x =1.

Теория.

Пусть в области V задана функция f (x, y, z) .

Разобьем область V поверхностями на малые, попарно не налегающие части Vk

V =V1 ... Vk ... Vn ,

с объемами ∆kV , и обозначим через d =max dk диаметр разбиения.

1≤k≤n

Выберем в каждой части промежуточную точку (ξk ,ηk ,ζk ) Vk .

Составим интегральную сумму

∑ f (ξk ,ηk ,ζk )∆kV .

k =1

Тройным интегралом называется предел интегральных сумм, когда диаметр разбиения стремится к нулю

	n
dlim→0	∑ f (ξk ,ηk ,ζk )∆kV = ∫∫∫f (x, y, z)dxdydz,
	k =1	V
		V

если он существует, конечен и не зависит ни от способа разбиения, ни от выбора промежуточных точек.

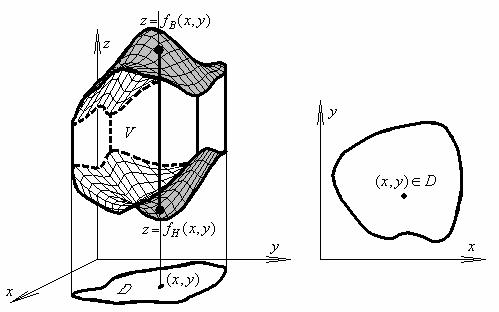
Физический смысл: масса (заряд) тела V с объемной плотностью ρ = f (x, y, z) .

n	n
m =∑	∆k m ≈∑ f (ξk ,ηk ,ζk )∆kV
k =1	k =1

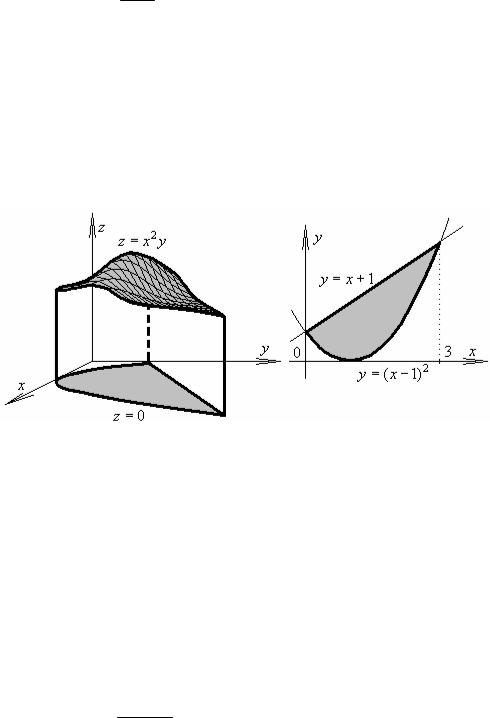
Если область V имеет вид “криволинейного цилиндра”,

V ={(x, y) D, fH (x, y) ≤z ≤ fB (x, y)},

то тройной интеграл может быть сведен к повторному:

∫∫∫f (x, y, z)dxdydz =∫∫(		fB (∫x, y)	f (x, y, z)dz )dxdy.
V	D	fH ( x, y)

Решения.

№ 34.1.

m =∫∫∫ρ (x, y, z)dxdydz =∫∫∫x3zy2 dxdydz =→

V V

Выделим среди поверхностей {z = x2 y, z =0, y =(x −1)2 , y = x +1}, ограничивающих объем V , те, уравнения которых не содержат переменной z . На плоскости xOy эти уравнения

задают некоторые кривые, а в пространстве – цилиндрические поверхности, параллельные оси Oz , в основании которых лежат эти кривые. В данном примере кривые

{y = (x −1)2 , y = x +1} ограничивают некоторую	область	D ,	так что	поверхности
{z = 0 ≤ z = x2 y, (x, y) D}, играющие роль	“нижней”	и	“верхней”,	достаточно
построить схематично.

V ={(x, y) D,

0 ≤ z ≤ x

y},

D ={0 ≤ x ≤ 3,

(

≤ y ≤ x +1},

−1

→=∫∫(

x2 y

)dxdy =∫∫x3 y2

x2 y

∫ x3 y2 dz

2 z

dxdy = 2

∫∫x3 y2

dxdy =

= 12 ∫∫x dxdy = 12 ∫3		(	x∫+1	x dy	)dx = 12 ∫3	(	x	x∫+1	1 dy
D	0		( x−1)2		0			( x−1)2

= 12 ∫(3x2

№ 34.2.

q =∫∫∫ρ (x,

− x3 ) dx = 12 (3 13 x3 − 14 x4 )	3	(33 − 14 34 )=

	0 = 12

y, z)dxdydz =∫∫∫ cos z dxdydz =→ sin x4 y2

)dx = 12 ∫3 x ((x +1)−(x −1)2 ) dx =

278 .

Выделим	среди	поверхностей	{z =π, z = x	4	y	2	,	y =	1	(	)
									2		x +1 , y =1, x =−1}

ограничивающих объем V , те, уравнения которых не содержат переменной z . В данном

примере прямые	{y =	1	(	)	ограничивают некоторую область D , так что
		2		x +1 , y =1, x =−1}
поверхности { z = x4 y2				≤ z =π, (x, y) D} , играющие роль “нижней” и “верхней”,

достаточно построить схематично.

<<< < Предыдущая 1 2 3 45 / 145 6 7 8 9 10 11 12 13 14 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
23.02.201534.74 Кб11маркетинг (робота с Ирой).docx
#
12.11.2019365.57 Кб9маркетинг услугТ 1-4.doc
#
23.02.201539.71 Кб5Маркетинг.docx
#
01.05.2019275.97 Кб3Маркетингова географія Л.1.doc
#
23.02.2015173.28 Кб16мат.методы.docx
#
23.02.20151.44 Mб69матан.pdf
#
23.02.20152.78 Mб86Матем. анализ. Методичка(1 семестр).doc
#
13.03.20161.44 Mб37Матеріали до словника 2.doc
#
13.03.2016105.98 Кб4материаловедение Лекция 1.doc
#
25.08.201938.33 Кб4Материалы 3_1.docx
#
10.11.2019241.66 Кб1материалы для лекции 1.doc